Mark goes to the grocery store and purchases items for $0.58, $1.25, $1.99, and $12.40. If Mark gives the cashier $20.00, how much change will he get back?
Answers
$0.58 + $1.25 + $1.99 + $12.40 = $ 16.22
After getting the sum of his purchases, subtract it to the $20.00 he gave to the cashier.
$20.00 - $16.22 = $3.78
The change Mark will get back is $3.78.
Related Questions
Suppose that a study of elementary school students reports that the mean age at which children begin reading is 5.4 years with a standard deviation of 0.8 years. Step 1 of 2: If a sampling distribution is created using samples of the ages at which 38 children begin reading, what would be the mean of the sampling distribution of sample means? Round to two decimal places, if necessary.
Answers
Answer:
According to the Central Limit Theorem, the sampling distribution of sample means would have a mean of 5.4 years.
Step-by-step explanation:
For a normally distributed random variable X, with mean and standard deviation, the sampling distribution of sample means with size n can be approximated to a normal distribution with mean and standard deviation.
As long as n is at least 30, the Central Limit Theorem can also be applied to skewed variables.
We have the following problem:
5.4 years is the average age for the entire population.Based on the Central Limit Theorem, 5.4 years would be the mean of the sampling distribution of sample means.Answer:
Step-by-step explanation:
The mean of the sampling distribution of sample means can be calculated using the formula:
μM = μ
where μ is the population mean and M is the sample mean.
Thus, μM = μ = 5.4 years.
Therefore, the mean of the sampling distribution of sample means would also be 5.4 years.
Find all values of m for which the equation has two real solutions.
3x² + 7x - (m + 1) = 0
ñ

Answers
Given equation to us is , \(3x^2+7x-(m+1)=0\) .
The given equation is a quadratic equation and it has two real solutions if it's discriminant is greater than or equal to 0 .
For a quadratic equation in standard form of \(ax ^{2} + bx + c = 0\)
the discriminant is given by b² - 4ac .
On comparing wrt to Standard form, we have ;
\(a = 3\)\(b = 7\)\(c = - (m+1)\)Hence we have,
\(\longrightarrow b^2-4ac \geq 0\\ \)
\(\longrightarrow 7^2-4(3)-(m+1)\geq 0\\\)
\(\longrightarrow 49 +12(m+1)\geq 0\\ \)
\(\longrightarrow 49 +12m+12\geq 0 \\ \)
\(\longrightarrow 12m \geq -61\\\)
\(\longrightarrow \underline{\underline{m \geq \dfrac{-61}{12}}} \)
Therefore the given quadratic equation will have real solutions for values of m greater than or equal to -61/12 .
And we are done!
In a popular online role playing game, players can create detailed designs for their character's "costumes," or appearance. Isabella sets up a website where players can buy and sell these costumes online. Information about the number of people who visited the website and the number of costumes purchased in a single day is listed below.
105 visitors purchased no costume.
41 visitors purchased exactly one costume.
8 visitors purchased more than one costume.
Based on these results, express the probability that the next person will purchase one or more costumes as a decimal to the nearest hundredth.
Answers
The probability that the next person will purchase one or more costumes can be found by dividing the number of visitors who purchased one or more costumes by the total number of visitors.
The total number of visitors is 105 + 41 + 8 = 154.
The number of visitors who purchased one or more costumes is 41 + 8 = 49.
So the probability that the next person will purchase one or more costumes is 49/154, which is approximately 0.32 to the nearest hundredth.
Find an equivalent expression 3(2d+2) + 2(2d+5)
PLSSSSS I need help
The options are
1.) 10d + 26
2.) -10d+ 26
3.) -10d-6
4.) 10d +16
5.) 10d - 4
thankyouuu
Answers
Answer:
10d+16
Step-by-step explanation:
=>3(2d+2)+2(2d+5)
=>6d+6+4d+10
=>10d+16
JK=2x+5 and KL=3x-8 find JL
Answers
Answer:
Step-by-step explanation:
3x -8 = 2x + 5
x - 8 = 5
x = 13
3(13) - 8 + 2(13) + 5
39 - 8 + 26 + 5
31 + 31 = 62
Does -a ? = (-a)?? Explain why or why not.
Answers
Explanation:
Always remember that variables have coefficients (x is the same as 1·x or 1x).
Raising a base to either an odd or even exponent has particular rules when it comes to signs:
If you raise -a² = -a² because a has a coefficient of - 1. This implies that -a² = -1a². Now, raising -a³ (odd exponent) still results in -a³ because you're only raising the base, a, to its exponent, and it doesn't include its coefficient of -1. Hence, -a³ = -1a³ = -a³.Also, (-a²) = -a² because once again, you're only raising the base, a, and not its coefficient (even if both are inside the parenthesis).It will be different if the base is raised as follows:
(-a)² = a² because the coefficient, -1, is included within the parenthesis. It is the same as (-1a)² = 1a² or a².(-a)³ = -a³ or -1a³ because it is an odd exponent, and if you raise a negative base to an odd exponent results in a negative value of the base.The key is that the exponent outside the parenthesis will affect both the coefficient and its base, such as (-a)².
Hope this makes complete sense.
Find Matrix mixed questions

Answers
The only matrix that is certainly symmetric is a)\((a^2 - b^2).\)
We know that a matrix A is symmetric if it is equal to its transpose, that is \(A = A^T.\)
a) \((a^2 - b^2)\)
We can write the transpose of this matrix as
\((a^2 - b^2)^T = (a^2)^T - (b^2)^T = a^2 - b^2\), which is equal to the original matrix. Therefore, this matrix is symmetric.
b) (A+B)(A-B)
Expanding this expression, we get \((A+B)(A-B) = A^2 - AB + BA - B^2.\)
Taking the transpose of this, we get \((A^2)^T - (AB)^T + (BA)^T - (B^2)^T = A^2 - BA + AB - B^2.\)
Since AB and BA may not be equal, we cannot say for certain that this matrix is symmetric.
c) ABA
Taking the transpose of this matrix, we get\((ABA)^T = A^T B^T A^T\). Since \(A^T and B^T\) may not commute, we cannot say for certain that this matrix is symmetric.
d) ABAB
Taking the transpose of this matrix, we get \((ABAB)^T = B^T A^T B^T A^T\). Again, since \(A^T and B^T\) may not commute, we cannot say for certain that this matrix is symmetric.
Therefore, the only matrix that is certainly symmetric is a) \((a^2 - b^2).\)
for such more question on matrix
https://brainly.com/question/25581637
#SPJ11
4 plums and 7 bananas
Answers
The graph of a function is given.
Is the function linear or nonlinear?
Select from the drop-down menus to correctly
complete the statement.
The function is Choose.
because it
Choose… have a constant rate of change.
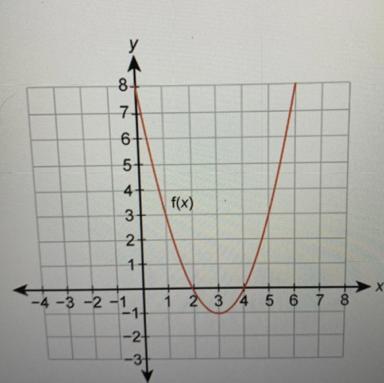
Answers
The function is nonlinear because it does not have a constant rate of change
The graph in the function is parabolic,
And the rate of change is -1.
What is function?Function is a combination of different types of variable and constants in which for the different values of x the value of function y is unique.
In the given graph,
Function f(x) is given.
The graph is curved shaped,
Implies that, it is not linear.
The graph shows function of parabola,
And the equation of the given parabola can be given as,
y = (x-3)² - 1.
To find the rate of change
Take points on tow points on x-axis,
x = 2 and x = 3
The value of y corresponding to x = 2,
y = 0,
The value of y corresponding to x = 3,
y = -1
The points are (2, 0) and (3, -1)
The rate of change = (-1 -0)/ 3 - 2 = -1 / 1 = -1
The rate of change is -1.
To know more about Function on:
https://brainly.com/question/2411204
#SPJ2
f(x) = 3x + 12, g(x) = 3x - 1;
=
=
Find (fºg)(x).
Answers
\(\text{Given that,}\\\\f(x) = 3x +12, ~ ~ g(x) = 3x -1\\\\(f \circ g)(x)\\\\=f(g(x))\\\\=f(3x-1)\\\\=3(3x-1) +12\\\\=9x - 3 +12\\\\=9x +9\\\\=9(x+1)\)
PLEASE DO IT it is due in 5 minutes

Answers
6*7=42. 6*2=12
b) 21y
11+4+6=21

Is 4(x + 2y) + 4x equal to 8(x + y)?
Yes or no
Answers
Answer:
Yes
4x + 8y + 4x = 8x + 8y
8x + 8y = 8x + 8y
Answer:
Yes
Step-by-step explanation:
First, simplify the two expressions by using the distributive property:
4(x + 2y) + 4x
Distribute 4 to the terms in the parentheses:
4(x + 2y) + 4x
4x + 8y + 4x
Add like terms:
8x + 8y
Then, do this to the other expression:
8(x + y)
8x + 8y
So, both expressions are equal, because they both simplified to 8x + 8y
how to mske a ten to find 17_8
Answers
A textbook store sold a combined total of 294 history and sociology textbooks in a week. The number of history textbooks sold was 86 more than the number
of sociology textbooks sold. How many textbooks of each type were sold?
Answers
Answer:
8
Step-by-step explanation:
Simplify
5x²-x+ 9 =
X=3

Answers
Answer:
51
Step-by-step explanation:
5x^2 - x + 9
5(3^2) - 3 + 9
5(9) + 6
45 + 6
= 51
Divide.
A. 2
B. 3
C. 2 r1
D. 3 r1
Answers
Answer: D
Step-by-step explanation:
Give an example of a number that is divisible by 9?
Answers
Answer:
9, 18, 27, 36, 45, 54, 63, 72, 81, 90 and many more
Have a great day and stay safe :)
) which statement about these triangles is true?
») There are exactly three isosceles
triangles.
» There are exactly three acute
triangles.
)) There are exactly three right triangles.
D
» There are exactly three scalene
triangles.

Answers
Hey there! I'm happy to help!
Isosceles triangles have at least two sides of the same length. We see that A and D are isosceles. It kind of looks like B does but if you look closely you will see that the there are not two matching sides.
Acute triangles have at least one angle that is less than 90 degrees. Triangles A and B are acute.
Right triangles have 1 right angle. Triangles C and D are right triangles.
Scalene triangles have sides of all different lengths. We see that B, C, and E are all scalene.
Therefore, the correct answer is There are exactly three scalene triangles.
Have a wonderful day! :D
Find the sum of the first 27 terms
of the arithmetic sequence.
First, fill in the equation.
a₁
= 5 and a27
Sn = 2/(a₁ + an)
Sn
=
[?]
2
+
=
83

Answers
Answer:
S₂₇ = 1188
Step-by-step explanation:
using the given formula for \(S_{n}\) , that is
\(S_{n}\) = \(\frac{n}{2}\) (a₁ + \(a_{n}\) )
with a₁ = 5 and \(a_{n}\) = a₂₇ = 83 , then
S₂₇ = \(\frac{27}{2}\) (5 + 83) = 13.5 × 88 = 1188
KEVIN HAS TWO PART-TIME JOBS. HE DELIVERS PIZZA FOR PEDRO'S PIZZERIA
AND MAKES $8 AN HOUR, PLUS $20 FOR DRIVING EXPENSES EACH WEEK. HE
ALSO DOES ODD JOBS FOR A LOCAL HARDWARE STORE, WHERE HE IS PAID $10
AN HOUR.
A. WRITE A SYSTEM OF EQUATIONS TO DESCRIBE THE SCENARIO WHERE H
REPRESENTS THE NUMBER OF HOURS KEVIN WORKS, AND A
REPRESENTS THE AMOUNT HE EARNS AT EACH JOB IN A WEEK. B. HOW MANY HOURS MUST KEVIN WORK AT EACH JOB SO THAT HIS EARNINGS FROM BOTH SIDES ARE THE SAME? C. WHAT WOULD HIS INCOME FROM EACH JOB BE IN THAT CASE?
Answers
Answer:
A. A = 8h + 10
A = 10h
B. 5 hours
C. $50
Step-by-step explanation:
A. https://brainly.com/question/17036764
Pizza Place: A = 8h + 10
Hardware Store: A = 10h
Since you had made a separate question for part A, I answered that.
B. Kevin's earnings is represented by A. Because we want the earnings for each job to be equal, set the two equations equal to each other. Solve for h.
8h + 10 = 10h
10 = 2h
5 = h
Kevin has to work 5 hours.
C. Plug 5 into each equation.
A = 8h + 10
A = 8(5) + 10
A = 40 + 10
A = 50
A = 10h
A = 10(5)
A = 50
Kevin will make 50 from each job.
The number of potholes in any given 1 mile stretch of freeway pavement in Pennsylvania has a bell-shaped distribution. This distribution has a mean of 42 and a standard deviation of 10. Using the empirical (68-95-99.7) rule, what is the approximate percentage of 1-mile long roadways with potholes numbering between 22 and 52
Answers
Answer:
81.5% of 1-mile long roadways with potholes numbering between 22 and 52
Step-by-step explanation:
The Empirical Rule states that, for a normally distributed random variable:
68% of the measures are within 1 standard deviation of the mean.
95% of the measures are within 2 standard deviation of the mean.
99.7% of the measures are within 3 standard deviations of the mean.
In this problem, we have that:
Mean of 42, standard deviation of 10.
The normal distribution is symmetric, so 50% of the measures are below the mean and 50% are above the mean
Approximate percentage of 1-mile long roadways with potholes numbering between 22 and 52:
22 = 42 - 2*10
So 22 is two standard deviations below the mean. Of the 50% of the measures that are below the mean, 95% are between two standard deviations below the mean(22) and the mean(42).
52 = 42 + 10
So 42 is one standard deviation above the mean. Of the 50% of the measures that are above the mean, 60% are between the mean(42) and one standard deviation above the mean(52).
In the desired interval, the percentage is:
\(P = 0.5*0.95 + 0.5*0.68 = 0.815\)
81.5% of 1-mile long roadways with potholes numbering between 22 and 52
Heights are generally normally distributed. Men have a mean of 69.5 inches and standard deviation 2.4 inches. Women have
a mean of 63.8 inches and standard deviation 2.6 inches. The US Air Force has a height requirement for their pilots to be
between 64 inches and 77 inches.
Make sure you are rounding z-scores properly to two places.
Part A: Find the two z-scores for women who meet this height requirement z =
and z=
I
(larger value)
For Blank 1
Part B: Using the z-scores from part A, find the proportion of women who meet the height requirement. Give this answer as a
decimal.
Z=
(smaller value)
Part C: Find the two z-scores for men who meet this height requirement z =
(larger value)
Part D: Using the z-scores from part C, find the proportion of men who meet the height requirement. Give this answer as a
decimal.
QUESTION 2
(smaller value) and
Part E: If the height requirement were changed to exclude only the shortest 1% of women and tallest 1% of men, what are the
new heights? The short value would be
in inches and the tall value would be
in inches. Please give these two values rounded properly to one decimal place.
Answers
Normal distribution curve is symmetric around the mean, it shows that values close to the mean happen more frequently than those distant from the mean.
What is meant by normal distribution curve?A bell-shaped (symmetric) curve, the normal probability distribution or the normal curve. The mean of it is represented by and the standard deviation by σ.
In this example, the mean and median are both equal and lie in the center of the distribution; they are 64, and the standard deviation is 7, with 68% of the values falling within the first standard deviation, 95% within the second standard deviation, and 99.7% within the third. Once more, variance is equal to the standard deviation squared.
According to the normal distribution curve:
"the percent of women whose heights are between 64 and 69.5 inches" represents the values within 2 standard deviation.
Area from a value (Use to compute p from Z)
Value from an area (Use to compute Z for confidence intervals)
Let the parameters be
Mean 64
Standard deviation 2.75
Above 1.96
Below 1.96
Between 64 and 69.5
Outside -1.96 and 1.96
Area (probability) 0.4772
And that value is 95 % of the whole data
To learn more normal distribution curve refer to:
https://brainly.com/question/15717360
#SPJ1

(Giving brainliest and 40 points)

Answers
Answer:
1360 m³
Step-by-step explanation:
To determine the volume of a compound 3D shape, divide the 3D shape into multiple 3D known shapes. Then, determine the volume of those "3D known shapes" and sum them up to determine the volume (figure).
In this figure, we can see two cuboids forming the figure. Therefore,
⇒ V (Figure) = V (Cuboid₁) + V (Cuboid₂)
The formula to determine the volume of a cuboid is the measure of the length, multiplied to the product of the width and the height.
⇒ V (Cuboid) = L × (W × H) or L × W × H
Therefore, the volume of cuboid₁ is;
⇒ V (Figure) = [L (Cuboid₁) × W (Cuboid₁) × H (Cuboid₁)] + V (Cuboid₂)
When we substitute the dimensions of the cuboid₁ , we get;
⇒ V (Figure) = [8 × 5 × 22] + V (Cuboid₂)
Which when simplified, we get;
⇒ V (Figure) = [880] + V (Cuboid₂)
The same should be done to cuboid₂. Therefore,
⇒ V (Figure) = [880] + [L (Cuboid₂) × W (Cuboid₂) × H (Cuboid₂)]
When we substitute the measures in the equation, we get;
⇒ V (Figure) = [880] + [8 × 5 × 12]
Which when simplified, we get;
⇒ V (Figure) = [880] + [40 × 12]
⇒ V (Figure) = [880] + [480]
⇒ V (Figure) = 1360 m³
Therefore, the volume of the figure is 1360 m³.
NO LINKS!!
The supply and demand curves for a business dealing with wheat are:
Supply: p = 1.55 + 0.00014x^2
Demand: p = (2.358 - 0.007x)^2
where p is the price in dollars per bushel and x is the quantity in bushels per day. Use a graphing utility to graph the supply and demand equations and find the market equilibrium. (The market equilibrium is the point of intersection of the graphs for x > 0. Round your answers to 2 decimal places.)
x= ________ bushels
p = $_________
Answers
Given curves:
p = 1.55 + 0.00014x²p = (2.358 - 0.007x)²See the attached, where both curves and their intersection is shown.
According to this we have:
x = 96.05p = $2.84
Answer:
x = 96.05 bushels
p = $2.84
Step-by-step explanation:
Graph the two equations (see attachment).
The market equilibrium is the point of intersection of the graphs for x > 0.
From inspection of the graph, the point of intersection is (96.05, 2.84).
Therefore:
x = 96.05 bushelsp = $2.84
Solve the system: 35x=3y+5 49x=4y+9
PLEASE HELP NEED ASAP
Answers
Answer:
x = 1
y =10
Step-by-step explanation:
ASAP
The average high temperatures in degrees for a city are listed.
58, 61, 71, 77, 91, 100, 105, 102, 95, 82, 66, 57
If a value of 80.8° is added to the data, how does the range change?
The range decreases to 44°.
The range increases to 52°.
The range stays 46°.
The range stays 48°.
Answers
If a value of 80.2° is added to the data, the range stays at 48º.
The mean of the data-set would change the most, and it would assume a value of 84º.
What is the mean and the range of a data-set?The mean of a data-set is given by the sum of all observations in the data-set divided by the number of observations. The range of a data-set is given by the difference between the highest value of the data-set by the smallest value of the data-set.
here, we have,
The highest and smallest high temperatures for the city are given as follows:
Smallest: 57º.
Highest: 105º.
Hence the range is obtained as follows:
105 - 57 = 48º.
80.2º would be neither the highest nor the smallest value in the data-set, which would then remain constant.
As it involves all values, it would be changed the most by changing the value of 58º to 101º, and would then assume a value of 84º.
More can be learned about the mean of a data-set at brainly.com/question/1136789
#SPJ1
In one county, the farms had a mean harvested area of 103 acres with a standard deviation of 9 acres.
What will be the mean and standard deviation of the distribution of area in square kilometers?
1 acre approximately equals 0.004 square kilometers.
A) Mean: 0.412 square kilometers
Standard deviation: 0.036 square kilometers
B) Mean: 0.412 square kilometers
Standard deviation: 9 square kilometers
C) Mean: 103 square kilometers
Standard deviation: 0.036 square kilometers
D) Mean: 103 square kilometers
Standard deviation: 9 square kilometers
Answers
Answer: A)
Step-by-step explanation: khan academy
Match the statement using the diagram

Answers
9514 1404 393
Answer:
d, b, c, a, e
Step-by-step explanation:
The order of the letters in the congruence statement tells you ...
ΔQOP ≅ ΔABC
∠Q ≅ ∠A
∠O ≅ ∠B ≅ 115°
∠P ≅ ∠C
QO ≅ AB = 5 m
OP ≅ BC = 8 m
PQ ≅ CA
a 24 foot tall streetlight casts a shadow that is 18 feet long. how long of a shadow is cast by a nearby parking meter post that is 4 feet high?
Answers
9514 1404 393
Answer:
3 ft
Step-by-step explanation:
The post is 4/24 = 1/6 as tall as the streetlight, so we expect its shadow to be 1/6 as long as that of the streetlight:
(1/6)(18 ft) = 3 ft
The parking meter post shadow is 3 feet long.
At the beginning of spring, Caroline planted a small sunflower in her
backyard. When it was first planted, the sunflower was 15 inches tall.
The sunflower then began to grow at a rate of 2.5 inches per week.
How tall would the sunflower be after 10 weeks? How tall would the
sunflower be after w weeks?
Height after 10 weeks:
Answers
Answer:
After 10 weeks: 40 inches
Step-by-step explanation:
Equation
15 + 2.5w = h
15 = beginning height
2.5 = rate per week
w = weeks passed
h = total height
Two or more expressions with an Equal sign is called as Equation.15+2.5W tall l would the sunflower be after w weeks and 40 inches tall after 10 weeks.
What is Equation?Two or more expressions with an Equal sign is called as Equation.
Given that, At the beginning of spring, Caroline planted a small sunflower in her backyard
The initial height of the sunflower was 15 inches tall.
The sunflower then began to grow at a rate of 2.5 inches per week.
We need to find the height of the tree after 10 weeks.
15+2.5(10)
15+25
40 inches tall after 10 weeks.
the sunflower height after w weeks
15+2.5W
Hence 15+2.5W tall l would the sunflower be after w weeks and 40 inches tall after 10 weeks.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ5