Meg has 2 berries, Paul has 2 berries, Mia has 5, Yen has 7, and April has 9. If they all put their berries together and then divide them up equally, how many will each one of them have?
Answers
Answer:
5
Step-by-step explanation:
You need to first add up all the berries: 2+2+5+7+9 which is 25.
There are 5 people so you need to divide 25 by 5: 25÷5 which is 5
So each person will have 5 berries each.
Related Questions
SOMEONEEE PLZ HELP 20 POINTS
JUST NEED HELP IN THE LAST4
Answers
Answer:
where is your questions

The following data values represent a population. What is the variance of the
values?
6, 10, 14,2
A. 16
B. 8
C. 10
D.20

Answers
Answer:
D is the correct answer.......
After drawing a square on the board, Mr. Hinkle asked his class to identify the shape. Timothy stated that Mr. Hinkle had drawn a rhombus. Which of the following statements is true?
Answers
No calculator Explanation please. Will choose brainliest. Pre-Calc. Lim as x approaches 9

Answers
The limit of the expression is determined as 0.
What is the limit of the expression?The limit of the expression is calculated as follows;
The given expression = lim (x ---> 9) [ ( x - 9 ) / √x - 3)
For the given limit in the expression, we have x maps to 9 or x tends to 9.
When x tends to 9, we will have;
x ---->9 = (9 - 9 ) / (√9 - 3)
= (0)/(-3 - 3)
note: since √x can be negative or positive, we will choose negative so that our solution will not be undefined.
= 0/-6
= 0
Learn more about limit expressions here: https://brainly.com/question/13027471
#SPJ1
\(\sf \longrightarrow \: \: \lim_{x\to \: 9} \: \: \: \frac{x \: - \: 9}{ \sqrt{x} - 3 } \\ \)
\(\sf \longrightarrow \: \: \lim_{ x\to \: 9} \: \: \: \frac{ ({ \sqrt{x} \: )}^{2} \: - \: {(3)}^{2} }{ \sqrt{x} - 3 } \\ \)
Now , by using Identity:-
a² - b² = ( a+b ) ( a-b )\(\sf \longrightarrow \: \: \lim_{ x\to \: 9} \: \: \: \frac{ ( \sqrt{x} + 3)( \sqrt{x} - 3)}{ \sqrt{x} - 3 } \\ \)
\(\sf \longrightarrow \: \: \lim_{ x\to \: 9} \: \: \: \frac{ ( \sqrt{x} + 3) \cancel{( \sqrt{x} - 3)}}{ \cancel{ \sqrt{x} - 3} } \\ \)
\(\sf \longrightarrow \: \: \lim_{ x\to \: 9} \: \: \: \frac{ ( \sqrt{x} + 3)(1)}{1 } \\ \)
\(\sf \longrightarrow \: \: \lim_{ x\to \: 9} \: \: \: ( \sqrt{x} + 3)(1) \\ \)
\(\sf \longrightarrow \: \: \lim_{ x\to \: 9} \: \: \: ( \sqrt{x} + 3)\\ \)
\(\sf \longrightarrow \: \: \lim_{ x\to \: 9} \: \: \: ( \sqrt{9} + 3)\\ \)
\(\sf \longrightarrow \: \: \lim_{ x\to \: 9} \: \: \: \sqrt{9} + 3\\ \)
\(\sf \longrightarrow \: \: \lim_{ x\to \: 9} \: \: \: 3 + 3\\ \)
\(\sf \longrightarrow \: \: \lim_{ x\to \: 9} \: \: \: 6\\ \)
I neeed help !!!!! :( someone help mee

Answers
Explanation:
If y is the short leg of the 30-60-90 triangle, then y*sqrt(3) is the length of the longer leg. The short leg is always opposite the shortest angle.
We're given that 5*sqrt(3) is the longer leg, so
y*sqrt(3) = 5*sqrt(3)
y = 5
After we divide both sides by sqrt(3)
Side note: x = 2y = 2*5 = 10.
\( \LARGE{ \underline{ \pink{ \sf{Required \: answer:}}}}\)
Heya mate!
If you observe the figure, the longest side always resides the opposite place of the right angle. Accordingly the perpendicular is 5√3 units in measure.
With this, the hypotenuse is x and the base is y. We need to find y. By doing some smart work! Let's guess the trigonometric ratio that we give us the relation between y and 5√3 because one of the angle given is 60°
⇛ tan a = Perpendicular / Base
Plugging the values of a, and Perpendicular to find the base of the triangle i.e. y.
⇛ tan 60° = 5√3 / y
⇛ √3 = 5√3 / y
⇛ y = 5√3 / √3
⇛ y = 5 units
Hence, the Correct Option is Option A.
3x+20=5x how many Solutions does it have
Answers
Answer:
one
Step-by-step explanation:
3x + 20 = 5x
20 = 5x - 3x
20 = 2x
x = 10
one solution
What is five percent of $97.25
Answers
Answer: 4.8625
Step-by-step explanation:
NO LINKS!! Please assist me with this problem Part 1m

Answers
Answer:
(x + 8)² + (y - 8)² = 64=======================
Given ConditionsTangent to x-axis,Tangent to y-axis,In the second quadrant,Radius is 8 units.SolutionEquation of circle:
(x - h)² + (y - k)² = r², where (h, k) is center and r - radiusThe center is the radius long distance from the x- axis to left and y-axis up same distance, this makes it in the second quadrant.
So the coordinates of the center are:
x = - 8, y = 8The equation is:
(x - (-8))² + (y - 8)² = 8²(x + 8)² + (y - 8)² = 64
Answer:
\((x+8)^2+(y-8)^2=64\)
Step-by-step explanation:
Required conditions:
Tangent to both axes.Center in the second quadrant.Radius = 8 units.If the circle is tangent to both axes, its center will be the same distance from both axes. That distance is its radius.
If the center of the circle is in quadrant II, the center will have a negative x-value and a positive y-value → (-x, y).
Therefore, the coordinates of the center will be (0-r, 0+r) where r is the radius.
If the radius is 8 units, then the center is (-8, 8).
\(\boxed{\begin{minipage}{4 cm}\underline{Equation of a circle}\\\\$(x-a)^2+(y-b)^2=r^2$\\\\where:\\ \phantom{ww}$\bullet$ $(a, b)$ is the center. \\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}\)
Substitute the found center and given radius into the formula to create an equation for the circle that satisfies the given conditions:
\(\implies (x-(-8))^2+(y-8)^2=8^2\)
\(\implies (x+8)^2+(y-8)^2=64\)

Which event is considered neither likely nor unlikely?
A, Rolling a number greater than 1 on a six-sided number cube.
B, Rolling a 1 on a six-sided number cube.
C, Getting heads when flipping a coin.
D, Choosing an X,Y, or Z from a bag containing all the letters of the alphabet.
Answers
According to the information, the event C, getting heads when flipping a coin, is considered neither likely nor unlikely.
Which event is considered neither likely nor unlikely?In probability, an event is considered likely if its probability is high, and it is considered unlikely if its probability is low. An event is considered neither likely nor unlikely if its probability is close to 0.5 or 50%. In this case we have to consider the probability of each option to establish a conclusion. Here is the analysis:
A, rolling a number greater than 1 on a six-sided number cube, has a probability of 5/6, which is greater than 0.5, so it is considered likely.B, rolling a 1 on a six-sided number cube, has a probability of 1/6, which is less than 0.5, so it is considered unlikely.C, getting heads when flipping a coin, has a probability of 1/2, which is equal to 0.5, so it is considered neither likely nor unlikely.D, choosing an X, Y, or Z from a bag containing all the letters of the alphabet, would depend on the specific contents of the bag. If the bag contains an equal number of each letter of the alphabet, the probability would be 3/26, which is less than 0.5, so it would be considered unlikely.According to the above, the event C, getting heads when flipping a coin, is considered neither likely nor unlikely because its probability is exactly 0.5 or 50%.
Learn more about probability in: https://brainly.com/question/31828911
#SPJ1
Find two 2 possible value of the geometric mean of 16 and 36
Answers
Answer:
\(\pm24\)
Step-by-step explanation:
To find the geometric mean of two numbers, you find their product and then take the square root of that product:
\(GM=\sqrt{16*36}=\sqrt{576}=\pm24\)
The 3D object above is sliced parallel to the base. What shape is formed?choice;rectangleoctagontrianglehexagon

Answers
If the figure is sliced parallel to the base, the figure formed is a hexagon.
Answer: hexagon
Answer:
Step-by-step explanation:
A hexagon is formed
Cliff takes out a $5,000 personal loan with 7
fixed annual interest compounded monthly to pay for his wedding. He repays the loan in 2 year.s
How much total interest does Cliff pay on his loan?
Answers
Cliff pays a total interest of approximately $679.90 on his $5,000 loan.
To calculate the total interest paid on the loan, we need to use the formula for compound interest:
\(A = P(1 + r/n)^{(nt)}\)
Where:
A is the final amount (loan amount + interest)
P is the principal (loan amount)
r is the annual interest rate (in decimal form)
n is the number of times interest is compounded per year
t is the number of years
Given that Cliff takes out a $5,000 loan with a fixed annual interest rate of 7% compounded monthly, we can substitute the values into the formula:
P = $5,000
r = 7% = 0.07
n = 12 (monthly compounding)
t = 2 years
\(A = 5000(1 + 0.07/12)^{(12 \times 2)\)
Calculating this expression:
A ≈ 5000\((1.00583)^{(24)\)
A ≈ 5000(1.13598)
A ≈ 5679.90
The final amount (A) is the loan amount plus the total interest paid. Therefore, to find the total interest paid, we subtract the principal (P) from the final amount (A):
Total Interest = A - P
Total Interest = 5679.90 - 5000
Total Interest ≈ $679.90
For similar question on total interest.
https://brainly.com/question/29415701
#SPJ8
What is the value of x?

Answers
The value of the angle x is 110 degrees
What is a transversal line?A transversal is described as a line that passes two lines of distinct points
Also, we need to know that pair of angles on a straight line sums up to 180 degrees.
Supplementary angles are described as angles that sum up to 180 degrees.
Corresponding angles are also equal, then, we have that;
70 + x = 180
collect the like terms, we get;
x = 180 - 70
subtract the values, we have;
x = 110 degrees
Learn more about transversals at: https://brainly.com/question/654982
#SPJ1
Which is the best estimate for 2 2/3 × 3 1/4
Answers
The sale of a new compact disc is $221 at a local discount store. At the store where this sale is going on, each new CD is in sale for $11 each. If Kyle purchased a player and some CDs for $265, how many CDs did he purchase?
Answers
ANSWER:
4 CDs
STEP-BY-STEP EXPLANATION:
According to the statement we can propose the following equation
\(\begin{gathered} 221+11x=265 \\ \text{ where x is the number of CDs} \end{gathered}\)Solving for x:
\(\begin{gathered} 11x=265-221 \\ x=\frac{44}{11} \\ x=4 \end{gathered}\)Which meanshe he buy 4 CDs
Keith is looking at a cliff. He determines that the angle of elevation to the top is 70° from where he is at. 70m away from Keith, Alan estimates the angle between the base of the cliff, himself, and Keith to be 29° while Keith estimates the angle between the base of the cliff, himself, and Alan to be 48°. What is the height, h, of the cliff to the nearest tenth of a metre?
1) 78.8m
2) 83.9m
3) 89.0m
4) 95.7m
This question completely baffled me on my homework, I still haven't done it because I don't even know how to approach it (Since it's a 3D problem)
Please help me out
Also, this homework is due in an hour so I'm starting to sweat
Answers
9514 1404 393
Answer:
4) 95.7 m
Step-by-step explanation:
The angle at the cliff base between Alan and Keith is ...
B = 180° -29° -48° = 103°
The law of sines will tell you the distance KB from Keith to the cliff base is
KB/sin(A) = KA/sin(B)
KB = KA×sin(A)/sin(B) = (70 m)sin(29°)/sin(103°) ≈ 34.82935 m
The height of the cliff is found from the tangent relation ...
Tan = Opposite/Adjacent
tan(70°) = height/(34.83 m)
height = (34.83 m)tan(70°) = 95.693 m
The height of the cliff is about 95.7 m.
_____
Additional comment
These problems can usually be resolved into two 2-D problems. Here, we can work out the distance we need from Keith to the cliff by considering only the ground plan of the site. Then we can work out the height of the cliff only considering the vertical plane containing Keith and the base of the cliff.
The attachment shows the ground plan triangle KAB.

60 units needed 14 units per case
Answers
what you mean bro??
Please help I been stuck on this question for so long

Answers
Answer: 1/ 3 ^9
Step-by-step explanation:
Answer:
1/39
Step-by-step explanation:
3-9=1/39
The answer is 0ne over three exponent nine
A student ran a distance of 3 1/2miles each day for 5 days. Then the student ran a distance of 4 1/4 miles each day for the next 5 days. What was the total distance in miles the student ran during these 10 days?
Answers
Answer:
To find the total distance, we need to add up the distance the student ran in the first 5 days and the distance the student ran in the next 5 days.
Distance for the first 5 days = 3 1/2 miles/day × 5 days = 17.5 miles
Distance for the next 5 days = 4 1/4 miles/day × 5 days = 21.25 miles
Total distance = Distance for the first 5 days + Distance for the next 5 days
Total distance = 17.5 miles + 21.25 miles
Total distance = 38.75 miles
Therefore, the student ran a total of 38.75 miles during these 10 days.
An employee who earns $12/hour, worked 37 hours this week, is paid a commission of $40 for each sale, and makes 9 sales during the same week, has earned total commissions of $ .
Answers
The total commission that's earned will be $360.
How to illustrate the expression?Expression simply refers to the mathematical statements which have at least two terms which are related by an operator and contain either numbers, variables, or both. Addition, subtraction, multiplication, and division are all possible mathematical operations.
In this case, an employee who earns $12/hour, worked 37 hours this week, is paid a commission of $40 for each sale, and makes 9 sales during the same week. Employees receive commission, also referred to as a sales commission, based on the sales they generate. A sales commission is a payment made to an employee after they successfully complete a task, typically selling a predetermined volume of goods or services. Sales commissions are a common incentive used by employers to boost employee productivity. A commission can be paid instead of or in addition to a salary.
The total commissions will be:
= Amount of commission × Number of sales
= $40 × 9
= $360
Learn more about expressions on:
brainly.com/question/723406
#SPJ1
A random sample of 1000 people was taken. Four hundred fifty of the people in the sample favored Candidate AT. The 95% confidence interval for the true proportion of people who favor Candidate A is a. .424 to .476. b. .419 to .481. c. .40 to .50. d. .45 to .55.
Answers
Answer:
\(0.45 - 1.96 \sqrt{\frac{0.45(1-0.45)}{1000}}=0.419\)
\(0.45 + 1.96 \sqrt{\frac{0.45(1-0.45)}{1000}}=0.481\)
And the 95% confidence interval would be given (0.419;0.481). And the best option would be:
b. .419 to .481
Step-by-step explanation:
We know the following info:
\(n = 1000\) sample size selected
\(X= 450\) represent the number of people who favored Candidate AT
The sample proportion would be:
\(\hat p=\frac{450}{1000}=0.45\)
The confidence interval would be given by this formula
\(\hat p \pm z_{\alpha/2} \sqrt{\frac{\hat p(1-\hat p)}{n}}\)
For the 95% confidence interval the value of \(\alpha=1-0.95=0.05\) and \(\alpha/2=0.025\), with that value we can find the quantile required for the interval in the normal standard distribution.
\(z_{\alpha/2}=1.96\)
And replacing into the confidence interval formula we got:
\(0.45 - 1.96 \sqrt{\frac{0.45(1-0.45)}{1000}}=0.419\)
\(0.45 + 1.96 \sqrt{\frac{0.45(1-0.45)}{1000}}=0.481\)
And the 95% confidence interval would be given (0.419;0.481). And the best option would be:
b. .419 to .481
Which statement about the location of √7 on the number line is true?
A= It is located at the number 7 on the number line.
B= It is located at the number 3.5 on the number line.
C= It is located between the numbers 2 and 3 on the number line.
D=It is located between the numbers 4 and 9 on the number line
Answers
Explanation
The square root of a number is “what number times itself”
2 x 2 = 4
3 x 3 = 9
7 is between 4 and 9 so C is the correct answer
Between which two integers is the value of √11?
9 and 10
5 and 6
7 and 8
O3 and 4
1 and 2
Answers
The square root of 11 is ?
The square root of 16 is 4
Between 3 and 4
PLS ANSWER CORRECTLY
The function f(x) = –3x2 + 36x – 119 written in vertex form is f(x) = –3(x – 6)2 – 11. Which statements are true about the graph of f(x)? Select three options.
A. The axis of symmetry is the line x = 6.
B. The vertex of the graph is at (–6, –11).
C. The parabola has a minimum.
D. The parabola opens down.
E. The value of h, when the equation is written in vertex form, is positive.
Answers
Answer:
A. The axis of symmetry is the line x = 6.
D. The parabola opens down.
E. The value of h, when the equation is written in vertex form, is positive.
Step-by-step explanation:
f(x) = –3(x – 6)^2 – 11.
This is in vertex form
y = a( x-h)^2 +k
where ( h,k) is the vertex
(6,-11) is the vertex, so line line of symmetry is x=6
a =-3 so the parabola opens down and it has a maximum
The value of h is 6, which is the x coordinate of the vertex
Answer:
A, D, EStep-by-step explanation:
f(x) = –3x2 + 36x – 119 written in
vertex form is f(x) = –3(x – 6)2 – 11
Vertex form is y = a(x - h)² + k
vertex is (h,k) which is (6, -11)
axis of symmetry x = 6where a = -3 because a<0, the parabola opens down.value of h = 6 as the vertex on the x coordinateWhat’s the number of unique ways that angel can pick and arrange songs for the playlist.

Answers
It is given that 10 out of 12 songs need to be selected first and then arranged in a playlist.
The permutation can be used for the arrangements.
The formula for permutation is:
\(_nP_r=\frac{n!}{(n-r)!}\)Here n is the total number of things and r is the total number of selections.
In this problem n=12, r=10 so the total number of arrangements is given by:
\(\begin{gathered} _{12}P_{10}=\frac{12!}{(12-10)!} \\ =\frac{12!}{2!} \\ =239500800 \end{gathered}\)Hence the total number of arrangements that can be made is 239500800.
Select the correct answer.
The branch manager of a clothing store is analyzing the average total bill of sale for his location. The national manager has communicated that
the overall population mean is $45.90 with a standard deviation of $10.3.1. The branch manager has a sample of 400 total bills of sale for his
location. By the central limit theorem, which interval can the branch manager be 95% certain that the sample mean will fall within?
Answers
Answer:
We can be 95% certain that the sample mean will fall within $44.87 and $46.93
Step-by-step explanation:
Empirical Rule:
68% of the measures are within 1 standard deviation of the mean.
95% of the measures are within 2 standard deviation of the mean.
99.7% of the measures are within 3 standard deviations of the mean.
Central Limit Theorem:
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Population:
Mean $45.90, standard deviation $10.31.
Sample:
By the Central limit theorem, mean $45.90, standard deviation \(s = \frac{10.31}{\sqrt{400}} = \frac{10.31}{20} = 0.5155\)
Which interval can the branch manager be 95% certain that the sample mean will fall within?
By the Empirical Rule, within 2 standard deviations of the mean. So
45.90 - 2*0.5155 = $44.87
45.90 + 2*0.5155 = $46.93
We can be 95% certain that the sample mean will fall within $44.87 and $46.93
PLEASE HELP ASAP
solve -1/6[3-15(1/3)2]
![PLEASE HELP ASAP solve -1/6[3-15(1/3)2]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/C0Nx4ldjSdyeTD1pu34mYu8d7IAOliwi.png)
Answers
Answer:
C) -2/9
Step-by-step explanation:
\(\displaystyle -\frac{1}{6}\biggr[3-15\biggr(\frac{1}{3}\biggr)^2\biggr]\\\\=-\frac{1}{6}\biggr[3-15\biggr(\frac{1}{9}\biggr)\biggr]\\\\=-\frac{1}{6}\biggr[3-\frac{15}{9}\biggr]\\\\=-\frac{1}{6}\biggr[\frac{27}{9}-\frac{15}{9}\biggr]\\\\=-\frac{1}{6}\biggr[\frac{12}{9}\biggr]\\\\=-\frac{1}{6}\biggr[\frac{4}{3}\biggr]\\\\=-\frac{4}{18}\\\\=-\frac{2}{9}\)
Answer:
Hence, Option (C) - 2/9 is the Answer:
Step-by-step explanation:
-1/6 [3 -15(1/3)^2]
-1/6(3 -15)(1/9))
-1/6(3 - 5/3)
-1/6 (4/3)
Hence, Option (C) - 2/9 is the Answer:
I hope it helps!
I need help with geometry! I need to find x and y, please help asp

Answers

Check the picture below.

The table shows three unique functions.
x f(x) g(x) h(x)
-2
4
6
-3
-1
1
2
1
4-
2
1
1
55 752
6
8
1
Hit
6:
Mark this and return
-25
Which statements can be used to compare the
characteristics of the functions? Select two options.
Of(x) has an all negative domain.
g(x) has the greatest maximum value.
All three functions share the same range.
Oh(x) has a range of all negative numbers.
All three functions share the same domain.
Answers
Answer:
The statements that can be used to compare the characteristics of the functions are:
1. g(x) has the greatest maximum value.
2. All three functions share the same domain.
Explanation:
- The table shows the values of three functions - f(x), g(x), and h(x) - evaluated at different values of x.
- We cannot determine the domain of f(x) or h(x) from the given table but we can see that g(x) has a domain of all real numbers.
- We can see that g(x) has the highest maximum value among the three functions, which is 8.
- We cannot determine the range of f(x) or g(x) from the given table but we can see that h(x) has a range of all negative numbers.
- We cannot say anything about the domain or range of f(x) based on the given table.
- Therefore, the two statements that can be used to compare the characteristics of the functions are: g(x) has the greatest maximum value and all three functions share the same domain.
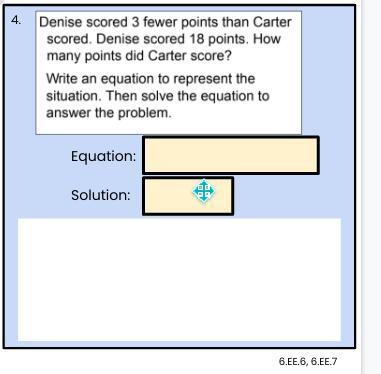
I NEED HELP PLZ WILL GIVE BRAINLYIST FOR CORRECT ANSWER (NO LINKS)
Answers
Answer:
Carter scored 21 points
Step-by-step explanation:
If Denise scored 3 fewer points, then you would add three to 18 to get the number of points that Carter scored.
18 + 3 = 21