Mrs. Smith spent $67.40 on groceries. The tax rate is 2%. What is the amount of sales tax?
Answers
Answer:
68.75
Step-by-step explanation:
to find the tax you multiply the total by the tax percentage 67.40 x .02 = 1.35
so the total for just tax is 1.35 so you add that to how much the groceries were originally
67.40+1.35=68.75
Related Questions
At a wedding there were 40 people from gromms side and 56 people from bride's family at the wedding
find the ratio of the groom's family to the bride's family at the wedding
Answers
Answer:
5 : 7
Step-by-step explanation:
groom's side: 40
bride's side: 56
ratio groom to bride = 40/56 = 20/28 = 10/14 = 5/7
Answer: 5 : 7
Explanation- 50+56 Is 106. So 106- 10=96.
There is your answer 96.
\(\sqrt{25} is an irrational
Answers
Answer:
Is Square Root of 25 Rational or Irrational?
Step-by-step explanation:
A rational number can be expressed in the form of p/q. Because √25 = 5 and 5 can be written in the form of a fraction 5/1. It proves that √25 is rational.
The answer is:
⇨ √25 is a rational numberWork/explanation:
What are rational numbers?
Rational numbers are integers and fractions.
Irrational numbers are numbers that cannot be expressed as fractions, such as π.
Now, \(\bf{\sqrt{25}}\) can be simplified to 5 or -5; both of which are rational numbers.
Hence, √25 is rational.PLEASE HELP ME YOU HAVE TO MAKE AN EQUATION LIKE y=mx+b!!!
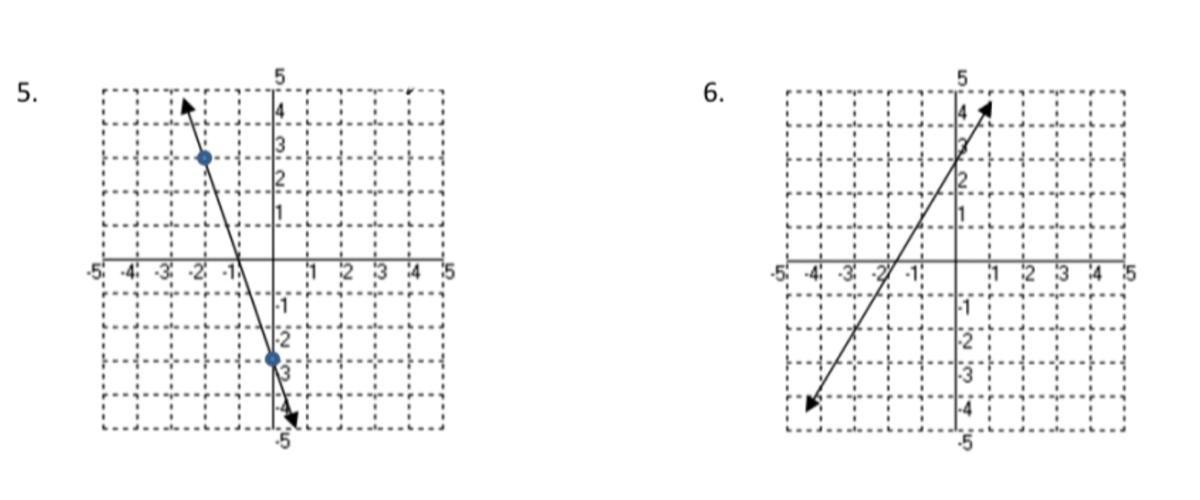
Answers
Answer:
5. y=-3x-3
6.y=5/3x+5
Step-by-step explanation:
you take the slope of the line and substitute it for x and take the y-intercept and sub it in for b
I hope this is right
1) The change in temperature from Wednesday to Thursday was -10°F. The
change in temperature from Thursday to Friday was -7°F. Which represents
a greater change in temperature?
The change from Wednesday to Thursday represents a bigger change in temperature.
The change from Thursday to Friday represents a bigger
change in temperature.
They are the same.
Answers
What I do understand of the quesetion, it should be "The change from Thursday to Friday represents a bigger change in temperature."
6.4 x 1.2 show your work
Answers
Answer:
7.68
Step-by-step explanation:
The mean length of the first 20 space shuttle flights was about 7 days, and the standard deviation was about 2 days. Using Chebychev’s Theorem, determine at least how many of the flights lasted between 3 days and 11 days.
Answers
At least 75% of the flights (or 15 out of the 20 flights) will last between 3 days and 11 days, according to Chebyshev's Theorem.
Chebyshev's Theorem states that for any given number k greater than 1, at least (\(1-\frac{1}{k^2}\)) of the data values in any data set will fall within k standard deviations of the mean.
In this case, we can use Chebyshev's Theorem to determine the minimum number of flights that lasted between 3 and 11 days.
Given:
Mean (μ) = 7 days
Standard Deviation (σ) = 2 days
To find the number of flights within the range of 3 to 11 days, we need to calculate how many standard deviations away from the mean these values are.
Lower Bound:
Value = 3 days
Number of standard deviations away from the
\(mean = \frac{(Value - Mean)}{ Standard Deviation}\)
\(mean =\frac{(3 - 7) }{2}\)
\(mean =\frac{-4}{2}\)
\(mean = -2\)
Upper Bound:
Value = 11 days
Number of standard deviations away from the
\(mean = \frac{(Value - Mean)}{Standard Deviation}\)
\(mean = \frac{(11 - 7)}{2}\)
\(mean = \frac{4}{2}\)
\(mean = 2\)
According to Chebyshev's Theorem, the minimum proportion of data values within k standard deviations of the mean is given by \((1- \frac{1}{k^2} )\).
So, we need to determine the proportion of data within 2 standard deviations, which is k = 2.
Proportion within 2 standard deviations = \(1-\frac{1}{2^2}\)
\(=1-\frac{1}{4}\)
\(= 1 - 0.25\)
\(= 0.75\)
Now, we can find the percentage of \(0.75\):
\(= 0.75\times 100\)
\(= 75\%\)
Therefore, at least 75% of the flights (or 15 out of the 20 flights) will last between 3 days and 11 days, according to Chebyshev's Theorem.
For such more questions on Chebyshev's Theorem
https://brainly.com/question/5179184
#SPJ8
Are in the ratio 1 ratio 2 ratio 3 and the sum of their cubes is 4500 Find the numbers?
Answers
The three numbers which are in the ratio 1:2:3 and whose sum of the cubes is 4500 are 5, 10, and 15.
As given in the question,
Let us consider three number which are in the ratio 1: 2 : 3 be,
y, 2y , and 3y.
As per given condition:
Sum of their cubes = 4500
⇒x³ + (2x)³ + (3x)³ = 4500
⇒ x³ ( 1 + 8 + 27 ) = 4500
⇒36x³ = 4500
⇒ x³ = 4500/36
⇒x³ = 125
⇒ x = ∛125
⇒ x = 5
⇒2x = 10
⇒3x = 15
Therefore, three numbers which are in the given ratio are given by 5, 10, 15.
The above question is incomplete, the complete question is :
Three numbers are in the ratio 1:2:3 and the sum of their cubes is 4500. Find the numbers.
learn more about ratio here
brainly.com/question/13419413
#SPJ4
Which value of x makes 5/6- x/6= 1/3?
Answers
Answer:
\(x = 3\)
Step-by-step explanation:
\( \frac{5}{6} - \frac{x}{6} = \frac{1}{3} \\ \\ \frac{5 - x}{6} = \frac{1}{3} \\ \\ 3(5 - x) = 6 \\ \\ 15 - 3x = 6 \\ \\ 3x = 15 - 6 \\ \\ 3x = 9 \\ \\ x = \frac{9}{3} \\ \\ x = 3\)
I hope I helped you^_^
Can anyone help? I’m sorry I’m bad at math-

Answers
5 students participated in a push-up competition.
The amount of push-ups each student completed is listed: 12, 7, 10, 11,5
What was the mean number of push-ups?
Answers
Answer: 9
Step-by-step explanation:
Formula : Mean = \(\dfrac{\text{Sum of observations}}{\text{Number of observaions}}\)
Given: 5 students participated in a push-up competition.
The amount of push-ups each student completed is listed: 12, 7, 10, 11,5.
Mean = \(\dfrac{12+7+10+77+5}{5}\)
\(=\dfrac{45}{5}=9\)
Hence, the mean number of push-ups = 9
A rectangular piece of iron has sides with lengths of 7.08 × 10–3 m, 2.18 × 10–2 m, and 4.51 × 10–3 m. what is the volume of the piece of iron? 6.96 × 10–7 m3 6.96 × 107 m3 6.96 × 10–18 m3
Answers
The volume of the rectangular piece with sides of lengths of 7.08 × 10–3 m, 2.18 × 10–2 m, and 4.51 × 10–3m is 6. 96 × 10^ -7 m
What is volume?Volume is defined as the amount of space or capacity occupied by a three-dimensional shape.
It is represented in cubic units.
How to determine the volume of a rectangleFormula:
Volume, V = length × breadth × height
Given the values;
7. 08 × 10 ^-3m , 2.18 × 10^ -2m and 4. 51 × 10^-3m
Multiply all the lengths
Volume = 7. 08 × 10 ^-3 × 2.18 × 10^ -2 × 4. 51 × 10^-3
= 69.6 × 10^-8
= 6. 96 × 10^ -7 m
Therefore, the volume of the rectangular piece is 6. 96 × 10^ -7 m
Learn more about volume of a rectangle here:
https://brainly.com/question/4062480
#SPJ1
Answer:
A
Step-by-step explanation:
trust
Find two prime numbers between 30 and 45.
Answers
Answer: PRIME NUMBERS BETWEEN 30 AND 45 ARE 31, 37, 41, and 43.
A person would like to create a 98% confidence interval for a particular unknown population proportion. They would like the interval to be accurate to within 3.0% and they believe a good estimate at the unknown population proportion is 0.40. How large of sample should they use in when creating this confidence interval?
Answers
A sample size of 753 would be required to create the desired 98% confidence interval with an accuracy of within 3.0%.
To determine the sample size needed to create a 98% confidence interval with an accuracy of 3.0%, we can use the formula:
n = (z^2 * p * (1-p)) / E^2
where:
n = sample size
z = z-score for the desired confidence level (98% = 2.33)
p = estimated population proportion (0.40)
E = desired margin of error (0.03)
Plugging in the values, we get:
n = (2.33^2 * 0.40 * (1-0.40)) / 0.03^2
n = 623.22
Rounding up to the nearest whole number, we get a sample size of 624. Therefore, the person would need to use a sample size of 624 in order to create a 98% confidence interval with an accuracy of 3.0% for the unknown population proportion.
To create a 98% confidence interval for an unknown population proportion with an accuracy of within 3.0% and an estimated population proportion of 0.40, you'll need to determine the required sample size. You can use the following formula for sample size calculation:
n = (Z^2 * p * (1-p)) / E^2
where n is the sample size, Z is the Z-score associated with the desired confidence level (98% in this case), p is the estimated population proportion (0.40), and E is the margin of error (3.0% or 0.03).
For a 98% confidence level, the Z-score is approximately 2.33. Plugging the values into the formula:
n = (2.33^2 * 0.40 * (1-0.40)) / 0.03^2
n ≈ 752.07
Since a sample size of 753 would be required to create the desired 98% confidence interval with an accuracy of within 3.0%.
To learn more about confidence interval, click here:
brainly.com/question/24131141
#SPJ11
Can someone plz helppppp m=?
B=?

Answers
A class has 7 boys and 10 girls. Select all associated ratios for this class
7:3
7:10
10:7
17:5
7:17
10:17
3.7
10:3
Answers
Answer:
10:17 (girls to total students)
7:17 (boys to total students)
10:7 (girls to boys)
7:10 (boys to girls)
Step-by-step explanation:
10:7
7:10 I think this is right
Find the sum of the measures of the intereor angles of each convex polygon.
Refer to attachment. BEST ANSWER WILL GET BRAINLY! fake answers will be reported and deleted.

Answers
Formula is
(n-2)180#1
\(\\ \sf\longmapsto (54-2)180\)
\(\\ \sf\longmapsto 52(180)\)
\(\\ \sf\longmapsto 9360°\)
#2
\(\\ \sf\longmapsto (19-2)180\)
\(\\ \sf\longmapsto 17(180)\)
\(\\ \sf\longmapsto 3060\)
#3
\(\\ \sf\longmapsto 292-2(180)\)
\(\\ \sf\longmapsto 290(180)\)
\(\\ \sf\longmapsto 52200\)
#4
\(\\ \sf\longmapsto (5-2)180\)
\(\\ \sf\longmapsto 3(180)\)
\(\\ \sf\longmapsto 540\)
Explain whether the pairing is a function

Answers
it would’ve been a function if it had many to one
The equation 9x−3x+1=k has two distinct real solutions precisely when k<−49 k<0 −49
Answers
The equation 9x − 3x + 1 = k has two distinct real solutions precisely when k < −49. Therefore, the equation 9x − 3x + 1 = k has two distinct real solutions precisely when k < −49/36.
Given equation is 9x − 3x + 1 = kLet us simplify the given equation9x − 3x + 1 = k⇒ 6x + 1 = k⇒ 6x = k − 1⇒ x = (k − 1) / 6
Now, the discriminant of the given quadratic equation isD = b² - 4ac= (-3)² - 4(9)(1-k)= 9-36(1-k)= - 27-36k
Let us analyze the given equation for different values of k
(i) k < −49/36, When k < −49/36, D > 0, the roots are real and distinct 9x − 3x + 1 = k⇒ 6x + 1 = k⇒ 6x = k − 1⇒ x = (k − 1) / 6
(ii) k = −49/36, When k = −49/36, D = 0, the roots are real and equal 9x − 3x + 1 = k⇒ 6x + 1 = k⇒ 6x = k − 1⇒ x = (k − 1) / 6
(iii) k > −49/36,When k > −49/36, D < 0, the roots are complex 9x − 3x + 1 = k⇒ 6x + 1 = k⇒ 6x = k − 1⇒ x = (k − 1) / 6
Thus, we can conclude that the equation 9x − 3x + 1 = k has two distinct real solutions precisely when k < −49/36.
Learn more about quadratic equation here:
https://brainly.com/question/30098550
#SPJ11
Julio says "If you subtract 13 from my number and multiply the difference by -6, the result is -144." What is Julio's number?
PLEASEEE HELPPP!!!!!!!
Answers
Answer:
37
Step-by-step explanation:
Reverse the steps
-144/-6 = 24
24 + 13 = 37
Find the margin of erur for the given values of e. 1 , and n. c=0.95,3+2.8,n=14 Click the icon to view the toistrbifion table. The margin of error is (Pound to one becrul plase as needed.)
Answers
The margin of error is Margin of Error = z * σ /√n = 1 * 0.8 / √14 = 0.213Pounding to one decimal place,Margin of Error ≈ 0.2Thus, the margin of error is 0.2 (Pound to one decimal place as needed).
Given: c
= 0.95, z
= 1, n
= 14 To find: Margin of Error Formula to be used:Margin of Error
= z * σ /√n where z
= z-value of the standard normal distributionσ
= Standard deviation of the population n
= Sample size Given n < 30, we can use t-distribution to find margin of error.We know,σ
= e / z where e
= margin of error Substituting the given values in the above formula, we getσ
= 3 + 2.8 / 6
= 0.8Using the t-distribution table, for 0.95 and 13 degrees of freedom (n-1), we get the t-value as 2.160.The margin of error is Margin of Error
= z * σ /√n
= 1 * 0.8 / √14
= 0.213Pounding to one decimal place,Margin of Error ≈ 0.2Thus, the margin of error is 0.2 (Pound to one decimal place as needed).
To know more about Margin visit:
https://brainly.com/question/28481234
#SPJ11
What is the value of y in the equation 2(3y plus 6 plus 3) equals 196 minus 16
Answers
Answer:
I got this question too! I'm not sure
Step-by-step explanation:
6. Carina has 24 apples, 36 bundles of bananas and 12 lemons. She wants to put all of the fruit into plastic containers, each with the same number of pieces of fruit in it. What is the greatest number of pieces of fruit she can put in each plastic container?
pls ayuda no entiendo ingles Flo
Answers
Solution:
Find the Highest Common Factor of 12, 24, and 36.
Highest Common Factor = 12
Divide.
\(12\div12=1\)
\(24\div12=2\)
\(36\div12=3\)
12 symbolizes the amount of baskets there are.
---------------------------------------------
Answer:
1 lemon per basket.
2 apple's per basket.
3 banana's per basket.
---------------------------------------------
There is no possible way that there can be the same amount of fruit in each basket.
---------------------------------------------
To find the greatest number of pieces of fruit that can be put in each plastic container, we need to find the greatest common divisor (GCD) of the given numbers. The GCD is the highest number that divides all the numbers evenly. In this case, the GCD is 12.
Explanation:To find the greatest number of pieces of fruit that can be put in each plastic container, we need to find the greatest common divisor (GCD) of the given numbers. The GCD is the highest number that divides all the numbers evenly. In this case, we want to find the GCD of 24, 36, and 12.
The prime factorization of 24 is 2 * 2 * 2 * 3. The prime factorization of 36 is 2 * 2 * 3 * 3. The prime factorization of 12 is 2 * 2 * 3.
The GCD is found by taking the common factors with the lowest exponent. So the GCD of 24, 36, and 12 is 2 * 2 * 3 = 12. Therefore, Carina can put 12 pieces of fruit in each plastic container.
Learn more about Greatest Common Divisor here:https://brainly.com/question/32851476
#SPJ3
easy question answer plssss

Answers
Answer:
Y = 1
Step-by-step explanation:
Proportional
Answer:
y=1
Step-by-step explanation:
Because they are proportional, the two points have to be equal if they were like a fraction. This means (15,3) would be 15/3 which is equal to 5. The other point is (5,?), so that means that the point will have to be 1. This is because then the point will be equal to 5.
Hope this helps
It is known that the length of a certain product X is normally distributed with μ = 18 inches. How is the probability P(X > 18) related to P(X < 18)?
Group of answer choices P(X > 18) is smaller than P(X < 18).
P(X > 18) is the same as P(X < 18).
P(X > 18) is greater than P(X < 18).
No comparison can be made because the standard deviation is not given.
Answers
The correct answer is, P(X > 18) is the same as P(X < 18). Option b is correct. The probability P(X > 18) is related to P(X < 18) in such a way that: P(X > 18) is the same as 1 − P(X < 18).
Explanation:
The mean length of a certain product X is μ = 18 inches.
As we know that the length of a certain product X is normally distributed.
So, we can conclude that: Z = (X - μ) / σ, where Z is the standard normal random variable.
Let's find the probability of X > 18 using the standard normal distribution table:
P(X > 18) = P(Z > (18 - μ) / σ)P(Z > (18 - 18) / σ) = P(Z > 0) = 0.5
Therefore, P(X > 18) = 0.5
Using the complement rule, the probability of X < 18 can be obtained:
P(X < 18) = 1 - P(X > 18)P(X < 18) = 1 - 0.5P(X < 18) = 0.5
Therefore, the probability P(X > 18) is the same as P(X < 18).
Hence, the correct answer is, P(X > 18) is the same as P(X < 18). Option b is correct.
Visit here to learn more about probability brainly.com/question/32117953
#SPJ11
I need help with this please

Answers
Answer:
The answer is B
Step-by-step explanation:
Because you are looking at the parallel lines not the strait cuz if it asked for the strait you would be adding.
a wood, rectangular box, with no top, is constructed with five panels that are each one centimeter thick. the external dimensions of the base are $16$ cm by $24$ cm, and the external height is $10$ cm. when the box is totally submersed in paint, how many square cm of painted surface will there be?
Answers
There will be 2216 square cm of the painted surface on the box, which is completely covered with paint.
Explain the term total surface area?The region that includes the base(s) as well as the curved portion is referred to as the total surface area. It is the overall area that the object's surface occupies. The total area of a shape with a curved base and surface is equal to the sum of a two areas.For the calculate of the area of rectangles:
Area = length * breadth
So, Outer area.
A1 = 2*16*10 + 2*24*10 + 1*16*24
A1 = 1184 sq.cm
Inner area:
A2 = 2*14*9 + 2*22*9 + 1*14*22
A2 = 956 sq. cm
Top area:
A3 = 16*24 - 14*22
A3 = 76 sq. cm
Complete area A = 1184 + 956 + 76
A = 2216 sq. cm
Thus, there will be 2216 square cm of the painted surface on the box, which is completely covered with paint.
To know more about the total surface area, here
https://brainly.com/question/16997207
#SPJ4

Which of the following is the equation in slope-intercept form for the line that passes through points (- 4, 1) and \ -3,0\; y = - x + 5; y = - x - 3; y = x + 2 None of these choices are correct
Answers
Answer:
there y= -x - 3 is correct
Step-by-step explanation:
(-4,1) ; (-3,0)
y= -x - 3
with (-4,1)
1 = -(-4) - 3 = 4 - 3 = 1. left = right
with (-3,0)
0 = -(-3) - 3 = 3 - 3 = 0. left = right
so the line y = -x - 3 is passes through points (-4,1) and (-3,0)
For the figure shown to the right, find the value of the variable and the measure of the angels
(it's a 4 part thing. so 4 answers should be shown)

Answers
Answer:
hope this answer helps you dear....take care!

Answer:
\(total \: angleof \: a \: triangle = 180 \\ then \\ x + 3x - 1 + x - 19 = 180 \\ 5x - 20 = 180 \\ 5x = 180 + 20 \\ 5x = 200 \\ x = \frac{200}{5} \\ x = 40 \\ thank \: you\)
-0.4a + 3 = 7
a = ?
Answers
-0.4a = 4
a = -10
Suppose X~ Beta(a, b) for constants a, b > 0, and Y|X = =x~ some fixed constant. (a) (5 pts) Find the joint pdf/pmf fx,y(x, y). (b) (5 pts) Find E[Y] and V(Y). (c) (5 extra credit pts) Find E[X|Y = y]
Answers
To find the joint PDF/PDF of X and Y, we'll use the conditional probability formula. The joint PDF/PDF of X and Y is denoted as fX,Y(x, y).
Given that X follows a Beta(a, b) distribution, the PDF of X is:
fX(x) =\((1/Beta(a, b)) * (x^_(a-1))\)\(* ((1-x)^_(b-1))\)
Now, for a fixed constant y, the conditional PDF of Y given X = x is defined as:
fY|X(y|x) = 1
if y = constant
0 otherwise
Since the value of Y is constant given X = x, we have:
fX,Y(x, y) = fX(x) * fY|X(y|x)
For y = constant, the joint PDF of X and Y is:
fX,Y(x, y) = fX(x) * fY|X(y|x)
=\((1/Beta(a, b)) * (x^_(a-1))\)\(* ((1-x)^_(b-1))\)\(* 1\) if y = constant
= 0 otherwise
Therefore, the joint PDF/PDF of X and Y is fX,Y(x, y)
= (1/Beta(a, b)) * (x^(a-1)) * ((1-x)^(b-1))
if y = constant, and 0 otherwise.
(b) To find E[Y] and V(Y), we'll use the properties of conditional expectation.
E[Y] = E[E[Y|X]]
= E[constant]
(since Y|X = x is constant)
= constant
Therefore, E[Y] is equal to the fixed constant.
V(Y) = E[V(Y|X)] + V[E[Y|X]]
Since Y|X is constant for any given value of X, the variance of Y|X is 0. Therefore:
V(Y) = E[0] + V[constant]
= 0 + 0
= 0
Thus, V(Y) is equal to 0.
(c) To find E[X|Y = y], we'll use the definition of conditional expectation.
E[X|Y = y] = ∫[0,1] x * fX|Y(x|y) dx
Given that Y|X is a constant, fX|Y(x|y) = fX(x), as the value of X does not depend on the value of Y.
Therefore, E[X|Y = y] = ∫[0,1] x * fX(x) dx
Using the PDF of X, we substitute it into the expression:
E[X|Y = y]
= ∫[0,1] x * [(1/Beta(a, b)) \(* (x^_(a-1))\)\(* ((1-x)^_(b-1))]\)\(dx\)
We can then integrate this expression over the range [0,1] to obtain the result.
Unfortunately, the integral does not have a closed-form solution, so it cannot be expressed in terms of elementary functions. Therefore, we can only compute the expected value of X given Y = y numerically using numerical integration techniques or approximation methods.
To know more about constants visit:
https://brainly.com/question/32200270
#SPJ11