Nate estimates that a search for websites about
music produces 500,000 websites. If this is a
12% increase over the previous year, explain
how you would find the number of websites for
the previous year. Then find the number of
websites the previous year.
Answers
Answer: 446,428.57 (rounded to hundredths
Step-by-step explanation:
I would find the number of websites of the previous year by using the formula : y = a(r)^t
\(500000 = a(1.12)^1\\\frac{500000}{1.12} = 446,428.571\)
Related Questions
The cost of 6 sandwiches and 4 drinks is $53. The code of 4 sandwiches and 6 drinks is $47. How much does one sandwich cost?
Answers
Answer:
$6.50
Step-by-step explanation:
SET UP A SYSTEM OF EQUATIONS WHERE SANDWHICHES IS REPRESENTED BY S AND DRINKS BY D:
6S+4D = 53
4S+6D=47
ADD THEM TOGETHER
10S+10D=100
SOLVE FOR D
10D = 100 - 10S
D = 10-S
SUBSTITUTE THAT VALUE INTO ONE OF THE ORIGINAL EQUATIONS
4S + 6(10-S) = 47
4S + 60 - 6S = 47
COMBINE LIKE TERMS
-2S + 60 = 47
SUBTRACT 60 FROM BOTH SIDES
-2S = -13
DIVIDE BY -2
S = 13/2
S = $6.50
Answer:
One sandwich is going to cost 6.50 while a drink is going to cost 3.50
Step-by-step explanation:
"We want to find and solve a system of equations to find the cost of one sandwich.
Each sandwich costs $6.50
We can start by defining the variables:
x = price of a sandwich
y = price of a drink.
Then from the given information we can write the equations:
6*x + 4*y = $53
4*x + 6*y = $47
We want to solve this for x, then we need to isolate y in one of the equations. Isolating y in the second equation we get:
y = ($47 - 4*x)/6
Now we can replace this in the other equation and solve it for x:
6*x + 4*($47 - 4*x)/6 = $53
6*x + $31.33 - (16/6)*x = $53
(20/6)*x = $53 - $31.33 = $21.67
x = (6/20)*$21.67 = $6.50" solved by
facundo3141592
PLEASE HELP!! GIVING PLENTY OF POINTS AND WILL REPORT THANKS!!!
The question is 1 b
Pia printed 2 maps of a walking trail. The length of the trail on the first map is 8 cm. The length of the trail on the second map is 6 cm.
A landmark on the first map is a triangle with length on the side of 3 mm, 4 mm, and 5 mm. What is the scale factor from the first map to the second map? What are the side lengths of the landmark on the second map? Show your work.
Will mark brainlyest if correct.

Answers
Answer: The scale factor from the first map to the second map is 4:3 (four to three) The side lengths of the landmark on the second map is 9/4 mm, 3 mm, 15/4mm.
Step-by-step explanation:
The scale factor is 8:6 which can be simplified to 4:3.
The side lengths of the landmark on the second map follows the same scale 4:3, so going in order:
4:3 = 3:x
4x = 9
x = 9/4
4:3 = 4:y
y = 3
4:3 = 5: z
4z = 15
z = 15/4
For what value of q is the equation – 13(q + 4) = 7q+ 16 true?
Answers
Answer:
q=-3.4
Step-by-step explanation:
Ashley sells 18.6 kg bags of mixed nuts that contain 60% peanuts. To make her product she adds peanuts to Brand A's mixed nuts which contain 20% peanuts. How much of each does she combine?
Answers
Answer:
She combines 9.3 kg of each.
Step-by-step explanation:
Let x = amount of brand A in kg
Let y = amount of peanuts in kg
First we deal with the amount of each product she uses.
"Ashley sells 18.6 kg bags of mixed nuts that contain 60% peanuts."
x + y = 18.6
Now we deal with just the amount of peanuts.
"To make her product she adds peanuts to Brand A's mixed nuts which contain 20% peanuts."
Brand A contains 20% peanuts, so x kg of brand A contains 0.2x kg of peanuts.
The peanuts she adds are pure peanuts, so all of y is peanuts.
The result is 18.6 kg of a mixture that is 60% peanuts, so the amount of peanuts in the bags she sells is 0.6 * 18.6 kg.
0.2x + y = 0.6 * 18.6
0.2x + y = 11.16
We have a system of equations:
x + y = 18.6
0.2x + y = 11.16
We have y in both equations, so let's subtract the second equation from the first equation to eliminate y.
0.8x = 7.44
Divide both sides by 0.8
x = 9.3
Plug in 9.3 for x in the first equation of the system and solve for y.
x + y = 18.6
9.3 + y = 18.6
y = 9.3
Answer: She combines 9.3 kg of each.
Convert from a percent to a decimal 8%
Answers
8% is equal to 0.08
Hope this helps, Sorry that it takes so long for people to get answers because of greedy people or people sending links.
c) Use your graph to find estimates of
the solutions to the equation
x? – X-2 = 3

Answers
Answer:
x = -1.791 and x = 2.791
Step-by-step explanation:
To solve this problem, we have to plot this graph using tool so we also know which of the lines is right.
The solution to this equation is at -1.791 and +2.791 and the graph that looks like the equation is the line in green color.
Quadratic EquationA given quadratic equation is an equation that has the highest degree of 2. Further more, when plotted on a graph, it has a parabolic shape.
The given equation is
\(3= x^2 - x - 2\\y = x^2 - x -5\)
Let's proceed to plot this graph and we would see the solutions at the point in which the lines curves.
Using that, the solution to this equation is at -1.791 and +2.791 and the graph that looks like the equation is the line in green color.
The solution are
-1.7912.791Learn more on quadratic equation here;
https://brainly.com/question/8649555
#SPJ2

your chronometer is set for greenwich mean time (gmt or universal time, ut). high noon at your present location is 9 pm ut. what is your longitude?
Answers
Your longitude in DMS is 135 degree. So the option D is correct.
This is because there are 12 hours left in the local time ( i.e. 12 hours noontime or mid-day).
As UT (or GMT) time is 9 p.m., there are 9 hours between GMT time and local time.
9 hours = 9 × 60 minutes = 540 minutes
Now, we know that:
Every four minutes, the Earth turns one degree.
Thus, 1-degree longitude difference = 4 minutes
Or, 4 minutes of time difference = 1 degree of longitude
Or, 1 minute of time difference = 1/4 degree of longitude
Or, 540 minutes of time difference = (1/4) × 540 degrees of longitude
540 minutes of time difference = 135 degrees of longitude
Also, we can infer that the current location is in the Western hemisphere because we know that it is 9 hours behind GMT (or UT) time.
Hence, the longitude of the current location = 135⁰
So the option 4 is correct.
To learn more about longitude link is here
brainly.com/question/30926134
#SPJ4
The complete question is:
Your chronometer is set for Greenwich Mean Time (GMT or Universal Tim, UT). High noon at your present location is 9 pm UT. What is your longitude in DMS (not decimal degrees)?
1. 30° 18'W
2. 30° 16'W
3. 30° 17'W
4. none of the above
An artist has been commissioned to make a stained glass window in the shape of a regular octagon. the octagon must fit inside an square space. determine the length of each side of the octagon. round to the nearest hundredth of an inch.
Answers
Using an assumed value that the octagon must fit inside an 11 inch square space, tthe length of each side of the octagon would be 8.23 inches.
Since an assumed side of the square is 11 inches
Here, y is the two equal sides of the right-angle triangle
So y + x + y = 11
Using Pythagoras's theorem for the right angle triangle
y² + y² = x²
2y² = x²
y² = (x²)/2
y = x /√2
So substitute the value of y = x /√2 in the equation
x /√2 + x + x /√2 = 11
2x /√2 + x = 11
2x /√2 + x√2 /√2 = 11
x[2/√2 + √2 /√2] = 11
x[(2 + √2) /√2] = 11
x(2 + √2) = 11√2
x = 11√2/(2 + √2)
x = 15.5563/3.4142 = 12.1421
Round to the nearest hundredth of an inch
x = 12.1
Learn more about the right triangle here:
https://brainly.com/question/28823211?referrer=searchResults
#SPJ4
Help me find the answer please ASAP

Answers
Answer:
in 45-45-90 triangle side opposite to 90 is a√2
Step-by-step explanation:
so the answer is C.3√2
put a=3
A soft-drink manufacturer claims that its 12-ounce cans do not contain, on average, more than 30 calories. A random sample of 16 cans of this soft drink, which were checked for calories, contained a mean of 31. 8 calories with a standard deviation of 3 calories. Assume that the number of calories in 12-ounce soda cans is normally distributed. Does the sample information support the manufacturer's claim? Use alpha=1% Select one: a. With test statistics of 2. 40 and critical value of 2. 602, we reject the null hypothesis. The manufacturer claims is not valid. B with test statistics of 2. 40 and critical value of 2. 326, we failed to reject the null hypothesis. The manufacturer claims can not be rejected. C. With test statistics of 2. 40 and critical value of 2. 326, we failed to reject the null hypothesis. The manufacturer claims is not valid. D. With test statistics of 2. 40 and critical value of 2. 602, we failed to reject the null hypothesis. The manufacturer claims can not be rejected
Answers
B. With test statistics of 2.40 and a critical value of 2.326, we fail to reject the null hypothesis. The manufacturer's claim cannot be rejected.
To test whether the sample information supports the manufacturer's claim that their 12-ounce cans do not contain more than 30 calories on average, we can use a one-sample t-test. The null hypothesis is that the true mean calorie content of the cans is equal to or less than 30 calories, while the alternative hypothesis is that it is greater than 30 calories.
Using the sample mean of 31.8 calories, the sample standard deviation of 3 calories, and a sample size of 16, we can calculate the t-value as follows:
t = (31.8 - 30) / (3 / √(16)) = 2.40
The degree of freedom for this test is 15 (n - 1). Using a significance level of alpha = 0.01 and a one-tailed test, the critical t-value is 2.602.
Comparing the calculated t-value of 2.40 to the critical t-value of 2.602, we can see that it falls within the non-rejection region. Therefore, we fail to reject the null hypothesis and conclude that the sample information does not provide enough evidence to support the manufacturer's claim that their 12-ounce cans contain, on average, less than or equal to 30 calories. The correct answer is B: with test statistics of 2.40 and a critical value of 2.326, we failed to reject the null hypothesis. The manufacturer's claims cannot be rejected.
Learn more about evidence here:
https://brainly.com/question/15880833
#SPJ11
Determine whether the relation is a function. Explain. y = 11 Multiple choice question. A) Yes; for any value x, the vertical line passes through no more than one point on the graph. B) Yes; for every value of x, the vertical line passes through more than one point on the graph. C) No; for every value of x, the vertical line passes through more than one point on the graph. D) No; for x = 11 , the vertical line passes through more than one point on the graph.
Answers
(B) Yes, the vertical line traverses multiple points on the graph for every value of x.
Since y = 11 has y as the output variable in addition to the input value of 11, it is a function.
We need an input variable or constant and an output variable or constant in order to have a function.
Given that there is an input value of c and an output value of y, the expression y = c is a function.
For each value of the input variable c, we can state that y equals c.
Since the expression y = 11 has both an input value of 11 and an output variable named y, we can infer that it is a function.
When we graph the expression, y = 11 it passes through the point ( 11, 0 ) and is parallel to the x-axis
For every value of x the vertical line passes through more than one point.
Learn more about function here:
https://brainly.com/question/11624077
#SPJ1
A microwave oven costs $124.85 before it is marked down. If it is marked down by 63%, what is its new price, to the
nearest cent?
A.$78.66
b. $61.85
C. $58.68
d. $46.19

Answers
Answer:
D ($46.19)
Step-by-step explanation:
$124.85 * (100% - 63%)
= $124.85 * 37 %
= $124.85 * 0.37
= 46.1945
= $46.19 (to the nearest cent)
Hope this helped!
Answer:
D: $46.19
Step-by-step explanation:
We did this math problem in my class already and I Remember the answer.
find the support and confidence of this transaction
A = I2, B = I3
Let 1 = {1,, I, I...... 1.} be a set of items, where I, denotes an item ID. Consider the transaction database D, defined in the table below: Transaction ID List of Items in the Transaction T₂ I, I,
Answers
For confidence interval: support of the association rule A to B is 0.5 and the confidence of the association rule A to B is 0.5.
For Support and confidence of the association rule A - B
To determine the support and the confidence of the association rule A → B, where A = {1, }, B = {1}, we use the formulas given below:
Support(A → B) = frequency of (A, B) / N
Confidence(A → B) = frequency of (A, B) / frequency of A
where N is the number of transactions in the database.
To find the frequency of (A, B) and the frequency of A.
Thus Frequency of (A, B) = 1
Since there is only one transaction in the database where both A and B occur, the frequency of (A, B) is 1.
Frequency of A = 2
The itemset {1, } occurs in two transactions T₁ and T₂.
Hence, the frequency of A is 2.
Learn more about confidence here:
brainly.com/question/30589291
#SPJ4
8-3 study guide and intervention special right triangles
Answers
Properties of Special right angled triangle,
a) If the leg of a 45°-45°-90° right triangle is x units, then the length of hypotenuse is x√2 units.
b) If a 30°-60°-90° right triangle the hypotenuse is twice the shorter leg, then longer leg is √3 times the shorter leg.
We have to discuss properties of special Right Triangles :
a) Properties of 45°-45°-90° Triangles : The sides of a 45°-45°-90° right triangle have a special relationship.
Example 1: If the leg of a 45°-45°-90° right triangle is x units, show that the hypotenuse is x√2 units.
Using the Pythagorean Theorem with
a = b = x, then c² = a² + b²
=> c² = x² + x²
=> c² = 2x²
=> c = √2x²
=> c = x√2
Thus, hypotenuse is x√2 units.
b) The sides of a 30°-60°-90° right triangle also have a special relationship.
Example 1: In a 30°-60°-90° right triangle the hypotenuse is twice the shorter leg. Show that the longer leg is √3 times the shorter leg.
∆MNQ is a 30°-60°-90° right triangle, and the length of the hypotenuse MN is two times the length of the shorter side NQ. Use the Pythagorean Theorem, c² = a²+ b²
let length of shorter side of ∆MNQ, NQ= x units, so, length of hypotenuse,MN = 2x
=> MN² = NQ² + MQ²
=> MQ² = MN² - NQ²
=> MQ² = (2x)² - x²
=> MQ² = 4x² - x² = 3x²
=> MQ = √3x²
=> MQ = √3 x = √3 NQ
So, longer side of right angled triangle is √3 times the short side.
To learn more about right angled triangle, visit:
https://brainly.com/question/64787
#SPJ4
Complete question:
8-3 study guide and intervention special right triangles
a) Properties of 45°-45°-90° Triangles
b) Properties of 30°-60°-90° Triangles


how do I know what side lengths equal a right triangle?
Answers
Answer:
if both the shorter ends are as long as or longer than the longer end when combined.
Step-by-step explanation:
Assume z is a standard normal random variable. What is the value of z if the area to the right of zis 9803? 0 -2.06 4803 0.0997 3.06
Answers
The value of z, In the above statistics-based question where the area to the right of z is 0.9803, is approximately 1.81.
In statistics, the standard normal distribution is a specific distribution of normal random variables with a mean of 0 and a standard deviation of 1. The area under the curve of a standard normal distribution is equal to 1, and the distribution is symmetric around the mean of 0.
To find the value of z for a given area to the right of z, we can use a standard normal distribution table or calculator. For example, using a standard normal distribution table, we can find the value of z that corresponds to an area of 0.0197 to the left of z. This value is approximately -1.81. Since the area to the right of z is 0.9803, we can find the value of z by subtracting -1.81 from 0, which gives us approximately 1.81.
Alternatively, we can use the inverse normal distribution function in Excel or another statistical software package to find the value of z directly. For example, the Excel function NORMSINV(0.9803) returns a value of approximately 1.81, which is the same as the value we obtained using the standard normal distribution table.
To learn more about Standard distribution, visit:
https://brainly.com/question/22920224
#SPJ11
EASY BUNCH OF POINTS & WILL GIVE BRAINLIEST:) Find the distance FG between the points F(2,7) and G(4, -1). Round your answer to the nearest tenth, if necessary. FG=
Answers
Answer:
2 between 2 and 4 and 8 between 7 and -1
Can you help me with the first 5 problems?

Answers
Sum is 2600 (for first question) , Sum is 2250 (for second question) , Sum is 1525 (for third question) , Sum is 16250 (for fourth question) , Sum is 385 (for fifth question) .
Here n= 25
1. Sequence: 200, 192, 184, 176
The comon diference (d) is = -8.
first term (a1) is 200.
The 25th term (\(a_2_5\)) = a1 +d (n -1)
\(a_2_5\) = 200+ (-8) (25 -1) = 200 -192 =8
sum = (n/2)(\(a_1\)+\(a_2_5\))
= (25/2) × (200 +8)
=25 × 104 =2600
2. Sequence is : 6+13+20 +27 +..
difference = (d) =7.
25th term (\(a_2_5\))= a1 +d (n -1)
(\(a_2_5\)) = 6 + 7(25-1)
=6+ 7×24
=174
Sum is =(n/2) (\(a_1\)+\(a_2_5\))
= 25/2 ×180
=2250
3. Sequence is : 13+17+21+25
difference = (d) = 4
25th term (\(a_2_5\))= a1 +d (n -1)
(\(a_2_5\)) = 13+4 (25-1)
= 13+ 4 (24)
= 109
Sum is =(n/2) (\(a_1\)+\(a_2_5\))
=25/2 × (13 +109)
=25/2 ×122
=1525
4. Sequence is :50, 100, 150, 200..
difference = (d)= 50
25th term (\(a_2_5\))= a1 +d (n -1)
=50+ 50 (25-1)
=50 +50×24
=1250
Sum is =(n/2) (\(a_1\)+\(a_2_5\))
=25/2 × (50+1250)
=25/2 × 1300
=16250
5. Sequence is= 1, 2.2, 3.4, 4.6, 5.8, ...
difference = (d)= 1.2
25th term (\(a_2_5\))= a1 +d (n -1)
=1+1.2 (25-1)
=1+1.2 (24)
=29.8
Sum is =(n/2) (\(a_1\)+\(a_2_5\))
=25/2 × (1+29.8)
=25/2 × 30.8
= 385
Leran more about the mean here
https://brainly.com/question/12373434
#SPJ1
Solve for X.
A. 10
B. 12
C. 15
D. 22

Answers
Answer:
B. 12Step-by-step explanation:
Since Z is midpoint of SR and Y is midpoint of QR, so as per triangle midpoint theorem ZY is parallel to SQ and measures half of its value:
SQ = 2ZY3x - 8 = 2(x + 2)3x - 8 = 2x + 43x - 2x = 4 + 8x = 12Correct answer choice is B
Answer:
the answer is B.12 ......
Please help me! thank you
Suppose an object is thrown upward with initial velocity of 48 feet per second from a high of 120 feet. The height of the object t seconds after it is thrown is given by h(t)=-16t^2+48t+120. Find the average velocity from t=2 to t=4.
Type your answer as a number with no units.
Answers
The average velocity from t = 2s to t = 4s would be - 48 ft/s.
What are algebraic expressions?In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context.
Mathematical symbols can designate numbers (constants), variables, operations, functions, brackets, punctuation, and grouping to help determine order of operations and other aspects of logical syntax.
Given is that an object is thrown upward with initial velocity of 48 feet per second from a high of 120 feet. The height of the object t seconds after it is thrown is given by h(t) = - 16t² + 48t + 120.
Average velocity
Average rate of change of velocity with time is called average velocity. Mathematically -
v{avg.} = Δx/Δt .... Eq { 1 }
Δx = x(4) - x(2)
Δx = - 16(4)² + 48(4) + 120 - {- 16(2)² + 48(2) + 120}
Δx = - 96
Δt = 4 - 2 = 2
So -
v{avg.} = Δx/Δt = -96/2 = - 48 ft/s
Therefore, the average velocity from t = 2s to t = 4s would be - 48 ft/s.
To solve more questions on functions, visit the link below-
brainly.com/question/17613163
#SPJ1
Decrease 210 by 45%
please give full working out thanks :)
Answers
Answer:
Step-by-step explanation:
210 - (0.45 * 210) = 116.5
Use cross products to identify the equation needed to solve this proportion: 5 x = 2 9
Answers
Answer:
The correct answer to this question is 2x = 45
Step-by-step explanation:
If you take 5 and multiply it by 9 you get 45. Therefore, 2x = 45 is the correct answer. (Also I know its right because I did the assignment and got this one right) Hope this helps :-)
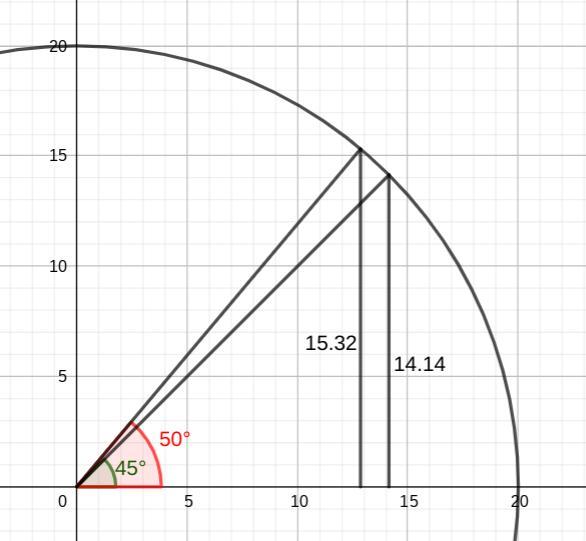
Help I'm not sure if this is the answer?
(This question is about trigonometric ratios)

Answers
9514 1404 393
Answer:
(b) 15.32
Step-by-step explanation:
You can use your triangle sense to answer this.
The side x will always be shorter than the hypotenuse, 20. This eliminates the last two choices.
If the angle is 45°, then the sides are equal at about 0.707 times the length of the hypotenuse. That would make them 0.707×20 = 14.14. Since the angle is greater than 45°, the opposite side will be greater than 14.14. Only one answer choice fits between 14 and 20: the second choice -- 15.32.
__
The mnemonic SOH CAH TOA reminds you of the relation ...
Sin = Opposite/Hypotenuse
sin(50°) = x/20
x = 20×sin(50°) . . . . multiply by 20 to find x
x ≈ 15.32 . . . . . . . . . use your calculator to evaluate
__
The attachment is intended to show how the triangle side lengths change with angle.
Which phrase should be inserted on the line to correctly compare the two fractions? Use the models to help. StartFraction 7 Over 8 EndFraction blank line StartFraction 2 Over 4 EndFraction StartFraction 7 Over 8 EndFraction StartFraction 2 Over 4 EndFraction A circle divided into 8 equal parts. 7 parts are shaded. A circle divided into 4 equal parts. 2 parts are shaded. is greater than cannot be compared to is less than is equal to
Answers
Answer:
7/8 is greater than 2/4
Step-by-step explanation:
In this question basically, what we are trying to do is to compare fractions and state which is greater or less.
The first fractions in the question is;
7/8 _ 2/4
Now, one of the best ways to go around comparing fractions is looking at the denominators.
In this question, the denominators in the fractions are 8 and 4.
The next thing to do here is to multiply the numerator and the denominator of the first by 4 and the numerator and the denominator of the second by 8. This makes it possible for us to have the same denominator in both fractions and thus compare both fractions directly.
Thus, what we have would be;
7/8 = 7/8 * 1 = 7/8 * 4/4 = 28/32
Now for the fraction;
2/4 = 2/4 * 1 = 2/4 * 8/8 = 16/32
We can see they both have a common denominator and we can directly compare their numerators.
Obviously, 28 is greater than 16 and this makes a case for the fact that 7/8 is greater than 2/4
So what we have in the blank is ; is greater than
Kindly note that the other part of the question that talks about shading circles is same as saying 7/8 and 2/4
Answer:
is less than
Step-by-step explanation:
look at da graph and watch mario.
HELP
Find the volume of the sphere in terms of Pi

Answers
Answer:
Hey there!
The volume of a sphere is 4/3pir^3
If d=5, then r=2.5,
Thus, we have 4/3(15.625)pi
20.83pi
The first choice is correct.
Hope this helps :)
Answer: num 1
Step-by-step explanation:
4/3*pi*r^3
4/3*pi*15.625
20.83*pi
hope i halped
can i get brainliest?(im trying to level up)
pls
-Zylynn
Transform the given function f(x) as described and write the resulting function as an equation.
compress horizontally by a factor of 3
translate left 1 unit
compress horizontally by a factor of 2
translate right 2 units
translate left 2 units
translate down 2 units
translate right 1 unit
translate up 3 units
expand vertically by a factor of 3
reflect across the x-axis
translate left 2 units
translate down 3 units
reflect across the x-axis
translate left 1 unit
compress vertically by a factor of 2
translate down 3 units
Answers
The given function, after applying the series of transformations, results in the following equation:
y = -3 * f(3(x + 1)) - 2 * f(2(x - 2)) - 2 - 3 * f(x + 1) + 3 - 3 * |f(x + 2)| - 1 * |f(x)| / 2 - 3
The series of transformations can be summarized as follows:
(1) Compress horizontally by a factor of 3 and translate left 1 unit: f(3(x + 1)).
(2) Compress horizontally by a factor of 2 and translate right 2 units: f(2(x - 2)).
(3) Translate left 2 units and translate down 2 units: f(x + 1) - 2.
(4) Translate right 1 unit and translate up 3 units: -3 * f(x + 2) + 3.
(5) Expand vertically by a factor of 3 and reflect across the x-axis: -3 * |f(x + 2)|.
(6) Translate left 2 units and translate down 3 units: -3 * |f(x + 2)| - 1.
(7) Reflect across the x-axis and translate left 1 unit: -1 * |f(x)| / 2.
(8) Compress vertically by a factor of 2 and translate down 3 units: -1 * |f(x)| / 2 - 3.
The resulting equation combines all these transformations to describe the final function.
Learn more about Function:
brainly.com/question/30721594
#SPJ11
I understand why the first question is (10 chose 5) but why in
the second one do we have to divide (10 chose 5) by 2
23. How many ways can a group of 10 girls be divided into two basketball teams (A and B say) of 5 players each? What if we don't name the teams?
Answers
The required number of ways is 126 ways.
The number of ways that a group of 10 girls can be divided into two basketball teams (A and B say) of 5 players each can be calculated by applying the formula nCr (combination).In order to get the number of ways, we need to calculate the number of combinations of choosing 5 girls out of 10 to form team A and the rest of the 5 girls will form team B.
The total number of ways can be found by the following formula:
nCr = n! / r! (n - r)!
where n is the total number of girls = 10 and r is the number of girls required for each team = 5
Thus, the number of ways that a group of 10 girls can be divided into two basketball teams (A and B say) of 5 players each will be: nCr = 10C5 = 252 ways.If we do not name the teams, then we have to divide the total number of ways by 2 because both teams will contain the same girls but just in a different order.
Thus, the required number of ways is given by:nCr / 2 = 10C5 / 2 = 252 / 2 = 126 ways.
Know more about combination here,
https://brainly.com/question/19692242
#SPJ11
A running track design is composed of two half circles connected by two straight-line segments. Garrett is jogging on the inner lane (with radius r) while Devin is jogging on the outer (with radius R). If r= 30 meters and R= 33 meters, how much longer does Devin have to run to complete one lap?
Answers
Answer:
18.86 m
Step-by-step explanation:
From the given question, both covers the same distance of the straight line segment.
For the inner lane,
length of arc of its semicircle = \(\pi\)r
= 30 x \(\frac{22}{7}\)
= 94.2857
So that,
the total length for the two halves of the inner lane = 2 x 94.2857
= 188.5714 m
For the outer lane,
length of arc of its semicircle = \(\pi\)r
= 33 x \(\frac{22}{7}\)
= 103.7143
The total length for the two halves of the outer lane = 2 x 103.7143
= 207.4286 m
The difference between the two = 207.4286 - 188.5714
= 18.8572 m
Therefore, Devin would run 18.86 m more to complete one lap.
Write the vector (3,9) as a linear combination of the unit vectors i and j.
Answers
The vector (3,9) as a linear combination of the unit vectors i and j is 3 * i + 9 * j
To write the vector (3, 9) as a linear combination of the unit vectors i and j, we need to find the coefficients that multiply the unit vectors to obtain the components of the given vector.
The unit vectors i and j represent the directions of the x-axis and y-axis, respectively. The vector (3, 9) can be expressed as:
(3, 9) = a * i + b * j
where a and b are the coefficients we need to find.
Since the unit vector i corresponds to the x-axis, the coefficient a represents the component of the vector (3, 9) in the x-direction. Similarly, the coefficient b represents the component of the vector (3, 9) in the y-direction.
To find the coefficients, we can equate the corresponding components:
3 = a
9 = b
Therefore, the vector (3, 9) can be written as:
(3, 9) = 3 * i + 9 * j
In this representation, the coefficient 3 indicates that the vector (3, 9) has a magnitude of 3 in the x-direction (i.e., parallel to the x-axis), and the coefficient 9 indicates that it has a magnitude of 9 in the y-direction (i.e., parallel to the y-axis).
To learn more about vector/linear combination click on,
https://brainly.com/question/29151684
#SPJ4
what is the awnser pls help

Answers
Answer:
I think its B 216
Step-by-step explanation:
Because you multiply 12×9×2 and get 216 (I dont know if im right)