Answers
Answer:
400 J
Step-by-step explanation:
Kinetic energy = ½ mv²
mass = 50 kg
velocity = 4 m/s
Kinetic energy = ½×50×(4)²
= ½×50×16
= 50×8
= 400 J
Option Four
\(mass(m) = 50kg \\ velocity(v) = 4ms {}^{ - 1} \\ kinetic \: energy = \frac{1}{2} mv {}^{2} \\ = \frac{1}{2} \times 50 \times (4) {}^{2} \\ = 400\)
Related Questions
If 0.142857142857......is expressed in the form m/n, then what is the value
of (2m + n)?
Answers
Answer:
The value will be: 1,285,713
Step-by-step explanation:
We have the number:
N = 0.142857...
Such that we have 6 decimals after the decimal point that repeat infinitely.
Then let's start by multiplying our number by 1,000,000 (same number of zeros as decimals after the decimal point)
Then we get:
1,000,000*N = 142,857.142857...
Now let's subtract N from both sides:
1,000,000*N - N = 142,857.142857... - 0.142857...
999,999*N = 142,857
Now let's isolate N
N = 142,857/999,999
Here is our number expressed in the form m/n, where:
m = 142,857
n = 999,999
Then the value of (2*m + n) is:
(2*142,857 + 999,999) = 1,285,713
Which of the following tables represents a linear function with the same slope as y=2-3x?

Answers
Table (C) represents the same slope -3 as the line y = 2 - 3x.
What is slope?The value of the steepness or the direction of a line in a coordinate plane is known as the slope of a line, often known as the gradient. Given the equation of a line or the coordinates of points situated on the straight line, slope can be determined using a variety of techniques.
The formula for slope between two points (x₁, y₁) and (x₂, y₂) is,
m = (y₂ - y₁)/(x₂ - x₁)
The given equation is,
y = 2 - 3x
The slope of the equation m = -3.
To find the slope of the table, take any two points, because given line is straight line. Therefore, slope will be equal for every point.
(A)
Slope m = (5-2)/(1-0) = 3
(B)
Slope m = (8-10)/ 4-2 = -2 / 2 = -1
(C)
Slope m = (7-10)/1-0 = -3.
Hence, slope of table (C) is -3.
To know more about Slope on:
https://brainly.com/question/16941905
#SPJ2
Function R gives the amount of rain measured by a rain gauge hours since it started raining. The amount of rain is measured in millimeters.
What does each expression or equation represent in this situation
a. R(3)
b. R(0.5)=14
Answers
Answer:
R(3) means that it has rained 3 millimeter and R(0.5)=14 means in 14 hours it has rained half a millimeter.
Step-by-step explanation:
The function R defines the amount of rain for a certain number of hours.
R(3) means the amount of rain in 3 hoursR(0.5) = 14 means the amount of rain in 0.5 hours is 14 millimetersThis function R can be represented as:
\(\mathbf{y = R(x)}\)
Where:
y represents the amount of rain, and x represents the time
So, the meaning of R(3) is:
The amount of rain in 3 hours
While the meaning of R(0.5) = 14 is:
The amount of rain in 0.5 hours is 14 millimeters
Read more about functions at:
https://brainly.com/question/6241820
How can you model an expression such as a − b?
Answers
can you please help me by today

Answers
Answer:
525 square yards
Step-by-step explanation:
\(31 \frac{1}{2} \times 16 \frac{2}{3} = \frac{63}{2} \times \frac{50}{3} \)
\(21 \times 25 = 525\)
find the quadratic function

Answers
For the quadratic function y = ax² + bx + c , for which graph passes through the points (2, 31), (3 , 45) , (1, 19) is given by y = x² + 9x + 9.
As given in the question,
Standard form of quadratic function,
y = ax² + bx + c
Graph of the quadratic function passes through the points (2, 31),
(3 , 45) , (1, 19) .
When passes through (2, 31)
31 = 4a + 2b + c __(1)
Passes through (3,45)
45 = 9a + 3b + c __(2)
Passes through (1, 19)
19 = a + b + c __(3)
Multiply 9 to (3) and subtract (2) from it,
9a + 9b + 9c =171
9a +3b + c = 45
6b + 8c = 126 ____(4)
Now, Multiply 4 to (3) and subtract (1) from it,
4a + 4b + 4c =76
4a +2b + c = 31
2b + 3c = 45____(5)
Multiply 3 to (5) and subtract (4) from it,
6b + 9c = 135
6b + 8c =126
c = 9
Substitute c= 9 in (5) we get,
2b + 3(9) = 45
⇒ b = 9
Now , substitute b = 9, c = 9 in (3) we get,
a + 9 + 9 = 19
⇒ a = 1
Required quadratic function is :
y = x² + 9x + 9
Therefore, for the quadratic function y = ax² + bx + c , for which graph passes through the points (2, 31), (3 , 45) ,(1, 19) is given by y =x² + 9x + 9.
Learn more about quadratic function here
brainly.com/question/18958913
#SPJ1
12 i
REASONING Target A has a circumference of 20 feet. Target B has a diameter of 3 feet. Both targets are the same
distance away. Which target is easier to hit?
Answers
Answer:
target a
Step-by-step explanation:
target b has a 6 ft. circumference
in an oral exam, a student is supposed to draw a card randomly from a set of 20 cards and answer all three questions on the selected card. mike is taking the exam. there are 8 favorable cards (mike knows answers for all 3 questions). mike will get a grade a if he answers all 3 questions. what is the probability for mike to get an a if he draws the card:
Answers
if Mike draws a card randomly, he has a 40% chance of getting a grade of "A".
The probability of an event is a numerical measure of the likelihood that the event will occur. It is expressed as a fraction or decimal between 0 and 1, where 0 indicates that the event is impossible and 1 indicates that the event is certain to occur. In this case, the event is Mike getting a grade of "A" on the oral exam, and the probability of this event is calculated as the number of favorable outcomes (cards with answers known by Mike) divided by the total number of possible outcomes (all 20 cards).
So, if Mike draws a card randomly from the set of 20 cards, he has a chance of 8/20 = 2/5 = 0.4 or 40% of answering all 3 questions correctly and getting a grade of "A". This means that if the experiment of drawing a card and answering the questions is repeated many times, Mike is expected to get a grade of "A" in 40% of those instances. The probability of Mike getting a grade of "A" is equal to the number of favorable outcomes (cards with answers known by Mike) divided by the total number of possible outcomes (all 20 cards).
Since Mike knows the answers to all 3 questions on 8 cards, the probability of him getting a grade of "A" is:
P(A) = 8/20 = 2/5 = 0.4 or 40%
So, if Mike draws a card randomly, he has a 40% chance of getting a grade of "A".
To know more about probability click here:
brainly.com/question/29381779
#SPJ4
Help me! I will give brainliest
Answers
Answer:
what happened
Step-by-step explanation:
Step by step explanation:
The midpoint of overline AB is M(3, 0) If the coordinates of A are (2, 4) what are the coordinates of B?

Answers
Answer: B(4,-4)
Step-by-step explanation:
M(3,0) A(2,4) B(x,y)=?
\(\displaystyle\\x_M=\frac{x_A+x_B}{2} \\\\Multiply\ both\ parts\ of\ the\ equation\ by \ 2:\\2x_M=x_A+x_B\\2x_M-x_A=x_A+x_B-x_A\\2x_M-x_A=x_B\\x_M=3\ \ \ \ \ x_A=2\\Hence,\\2*3-2=x_B\\6-2=x_B\\4=x_B\\Similarly:\\2y_M-y_A=y_B\\y_m=0\ \ \ \ \ y_A=4\\Hence,\\2*0-4=y_B\\0-4=y_B\\-4=y_B\\Thus,\ B(4,-4)\)
EASY!!!!!! ILL MARK BRAINLIEST

Answers
Answer:
-2a (small 2) + 4a - 8
Step-by-step explanation:
Find the surface area of each prism

Answers
Answer:
3. SA = 876 \(in^{2}\)
4. SA = 161 \(ft^{2}\)
Step-by-step explanation:
Number 3.
To find the total Surface Area, we need to know all the side lengths which are used to multiply to find the Area of each side. Then add the areas of all the sides to get the total SA.
To find side lengths:
Assuming the back triangle (24, 10 in) is congruent to the front triangle (26in.): First, Knowing the Pythagorean triples or the Pythagorean theorem, we can conclude that the short bottom leg in the triangle on the right (6, 10, x in) is 8 in. Secondly, to find the leg of the triangle with a hypotenuse of 24 inches, we subtract: 26 - 8 = 18 in.
Now we know all the (needed) side lengths.
To find the Surface Area:
Total SA = (12 x 26) + (12 x 24) + (12 x 10) + 2 x ((6 x 18 x 0.5) + (6 x 8 x 0.5))
= 312 + 288 + 120 + 2 x (54 + 24) = 720 + (2 x 78)
= 876 \(in^{2}\)
Number 4.
Same Idea: To find the Total SA, we need to know all the side lengths which are used to multiply to find the Area of each side. Then add the areas of all the sides to get the total SA.
Assuming the back triangle (7ft) is congruent to the front triangle (5x5 ft), then in this case, we already know all the needed side lengths.
To find the Surface Area:
Total SA = 2 x (8 x 5) + 2 x (5 x 5 x 0.5) + (7 x 8)
= 80 + 25 + 56
= 161 \(ft^{2}\)
What Is the slope of the line on the graph?

Answers
Answer:
2/4 which simplifies to be 1/2
Step-by-step explanation:
lmk if you wanna know how I got the answer, pretty simple to understand remember rise over run aka y/x.
Just giving you a heads up!
Bernice decides to look at a Horizon Unwired phone plan. The plan has a monthly charge and an activation fee. With this plan, she can get 10 months of service for $210 and 15 months of service for $292. 50.
•Write a linear equation to represent the cost of the plan. Let C represent the total amount of money paid in dollars, and m represent the number of months of service. Show work.
•Use your equation to find the cost for 24 months of service.
Due to inflation, Horizon Unwired will increase either the activation fee by 50% OR increase the monthly charge by 10%.
•Which change would cost Bernice less money over two years? Support your reasoning with numbers and words
Answers
The linear equation to represent the cost of the plan is C = 16.5m + 45 , the cost for 24 months of service is $441 and Bernice should choose activation fee increased by 50% .
In the plan, Bernice can get 10 months of service for $210 and 15 months of service for $292.50 ,
then the above situation can be represented as : (10, 210) , (15, 292.50),
Let C = total amount of money paid and m = number of months of service.
Using these two points, the slope of line ,
⇒ Slope = (292.50 - 210)/(15 - 10) = 82.5/5 = 16.5 ,
Now, we use the point (10,210) and the slope = 16.5 to write the equation of the line in point-slope form ,
⇒ C - 210 = 16.5(m - 10) ,
⇒ C - 210 = 16.5m - 165
⇒ C = 16.5m + 45,
So, the linear equation for cost of Horizon Unwired phone plan is C=16.5m+45.
To find the cost of 24 months of service, we substitute m = 24 into the equation:
We get , C = 16.5×24 + 45= 396 + 45 = 441,
So, the cost for 24 months of service is $441.
Consider the scenario1 :
There is increase in activation fee by 50%:
It would become : $45 × 1.5 = $67.50
But the monthly charge remains the same.
So, total cost of plan for 24 months of service ;
⇒ C = (16.50 × 24) + $67.50
⇒ C = $463.50
Consider the Scenario2 :
Increase in monthly charge by 10%:
It would become : $16.50 × 1.1 = $18.15 ,
But the activation fee remains the same.
So, total cost of plan for 24 months of service is ;
⇒ C = ($18.15 × 24) + $45
⇒ C = $480.60
Comparing the two scenarios, we can see that it would cost Bernice less money over two years if the activation fee is increased by 50%.
Therefore, Bernice should choose to have the activation fee increased by 50% instead of monthly charge increased by 10%.
Learn more about Linear Equations here
https://brainly.com/question/27866747
#SPJ4
Find the 49th term.
-15, -10, -5, O, 5, ...
49th term = [?]
1st term + common difference(desired term - 1)
Enter
Answers
Answer:
49th term = 225
Step-by-step explanation:
The following sequence: -15, -10, -5, 0, -5... is an example of an arithmetic progression.
An arithmetic progression or AP for short, is a sequence in which the difference between successive terms is constant. This difference is known as the common difference, and can be found by subtracting a term by its preceding term.
The general formula, for the nth term of an arithmetic progression, is thus:
Tn = a + (n - 1)d, where a = first term, and d = common difference.
In the sequence: -15, -10, -5, 0, 5...,
a = -15, and d = -10--15 = 5
T49 = -15 + (49 - 1)5 = 225
∴ 49th term = 225
FIND THE MOST GENERAL ANTL DERIVATIVE OF \( f(x)=\sin X \)
Answers
The most general antiderivative of \( f(x) = \sin(x) \) is \( F(x) = -\cos(x) + C \), where \( C \) represents the constant of integration.
The derivative of \( F(x) \) is indeed \( f(x) \) since the derivative of \(-\cos(x)\) is \(\sin(x)\) and the derivative of the constant \( C \) is zero.
In calculus, the antiderivative of a function represents the set of all functions whose derivative is equal to the original function. In this case, the derivative of \( -\cos(x) \) is \( \sin(x) \), and the derivative of any constant \( C \) is zero. Thus, the antiderivative of \( f(x) = \sin(x) \) is given by \( F(x) = -\cos(x) + C \), where \( C \) can be any real number. Adding the constant of integration allows us to account for all possible antiderivatives of \( f(x) \).
For more information on antiderivative visit: brainly.com/question/32562856
#SPJ11
[HELP!!]
A circle has a radius of 6 ft.
What is the area of the sector formed by a central angle measuring 5π3 radians?
Use 3.14 for pi.
Answers
Answer:
\(\sf area \ of \ sector = 94.25 \ ft^2\)
Explanation:
\(\sf area \ of \ sector = \frac{1}{2} r^2 \theta\)
using the formula:
\(\hookrightarrow \sf area \ of \ sector = \frac{1}{2} r^2 \theta\)
\(\hookrightarrow \sf area \ of \ sector = \frac{1}{2} (6)^2 (\frac{5\pi }{3} )\)
\(\hookrightarrow \sf area \ of \ sector = 30\pi\)
\(\hookrightarrow \sf area \ of \ sector = 30(3.14)\)
\(\hookrightarrow \sf area \ of \ sector = 94.25 \ ft^2\)
PLEASE is due very soon please explain

Answers
Answer:
1) The image of the line has the same slope as the pre-image but a different y-intercept.
hope this helps ;)
list five perfect squares.
Answers
Perfect squares are numbers gotten by squaring whole numbers. Therefore, 5 exmaples of perfect squares are
4(2^2)
9(3^3)
16(4^4)
25(5^5)
49(7^7)
So 5 perfect squares are 4, 9, 16, 25, 49
∠A and ∠B are supplementary such that
m∠A
=2x-2 and m∠B=4x+2
Write an equation that can be used to find the value of x? Find the value of x and the measure of ∠A?
Equation ___________________
x = _______________________
Answers
Answer:
The equation is;
(2x-2) + (4x + 2) = 180
x = 30
m∠A = 58
Step-by-step explanation:
Mathematically, when two angles are supplementary, the values of both angles add up to be 180
From
what we have here;
(2x -2) + (4x + 2) = 180
2x -2 + 4x + 2 = 180
6x = 180
x = 180/6
x = 30
Recall;
The measure of angle A is as follows;
2x -2 = 2(30) - 2 = 60-2 = 58
How far from the base of a house should you place an 18-foot ladder if it is to reach a window that
is 15 feet high?
Answers
I need help please!!!
At the beginning of the year there were 24 students in rocketry club. By the end of the year the number of students increased by 50%. How many student are in the club at the end of the year.
Answers
Please help I don’t understand

Answers
The solution for x is x = (y - 5) / 3.
To solve the equation y = 5 + 3x for x, we need to isolate the variable x on one side of the equation. Here's the step-by-step solution:
Start with the equation: y = 5 + 3x.
Subtract 5 from both sides to isolate the term with x:
y - 5 = 5 + 3x - 5.
Simplifying:
y - 5 = 3x.
Divide both sides by 3 to solve for x:
(y - 5) / 3 = 3x / 3.
Simplifying:
(y - 5) / 3 = x.
So, the solution for x is x = (y - 5) / 3.
Learn more about Equation here:
https://brainly.com/question/29657983
#SPJ1
find the net change in the value of the function between the given inputs. f(x) = 6x − 5; from 1 to 6
Answers
The net change in the value of the function between x = 1 and x = 6 is 30.
To find the net change in the value of the function between the inputs of 1 and 6, we need to find the difference between the output values of the function at x = 1 and x = 6, and then take the absolute value of that difference.
First, we can find the output value of the function at x = 1:
f(1) = 6(1) - 5 = 1
Next, we can find the output value of the function at x = 6:
f(6) = 6(6) - 5 = 31
The net change in the value of the function between x = 1 and x = 6 is the absolute value of the difference between these two output values:
|f(6) - f(1)| = |31 - 1| = 30
Therefore, the net change in the value of the function between x = 1 and x = 6 is 30.
To learn more about net change visit: https://brainly.com/question/29989249
#SPJ11
The manager would like to know the probability of a stockout during replenishment lead-time. in other words, what is the probability that demand during lead-time will exceed 25 gallons?
Answers
The probability that demand during this period will exceed 25 gallons depends on the distribution of demand.
To calculate the probability of a stockout during the replenishment lead-time, we need to consider the distribution of demand during this period. If the demand follows a known probability distribution, such as the normal distribution, we can use statistical methods to estimate the probability.
First, we need to determine the parameters of the distribution, such as the mean and standard deviation of the demand during the lead-time. Once we have these parameters, we can calculate the probability of demand exceeding 25 gallons using the cumulative distribution function (CDF) of the chosen distribution.
For example, if the demand during lead-time follows a normal distribution with a mean of 20 gallons and a standard deviation of 5 gallons, we can use the normal distribution table or statistical software to find the probability of demand exceeding 25 gallons.
Alternatively, if we have historical data on demand during lead-time, we can use that data to estimate the probability. We can calculate the proportion of instances where the demand exceeded 25 gallons and use this as an estimate of the probability of a stockout during the lead-time.
Overall, the probability of a stockout during replenishment lead-time depends on the distribution of demand and can be determined using statistical techniques or historical data.
Learn more about probability here:
https://brainly.com/question/23417919
#SPJ11
-16 - (-30) = ?
please help me, i cant figure it out
Answers
Answer: 14
Step-by-step explanation:
1. Add the two negative sign together to make a plus:
-16 + 30
2. Do the math
-16 + 30 = 14
Answer:
-14
Step-by-step explanation:
All you need to do is subtract the 2 numbers without the negitv then when your done add the negitve
What is the range of this function?

Answers
Range of the function can be defined as [0, infinity)
Given,
Graph of a function.
Range is the set of all the possible output values of the functions represented on y axis.
y - axis values ranges from 0 to infinity .
Thus the range can be defined as [ 0 , infinity ) .
Note
0 will be included in the range because the dot is shaded at (-5 , 0) .
Know more about range,
https://brainly.com/question/17440903
#SPJ1
Suppose X₁.....Xn is a sample of successes and failures from a Bernoulli population with probability of success p. Let Ex=288 with n=400. Then a 90% confidence interval for p is: a) .720.044 b) .720
Answers
The calculated confidence interval so it is a possible value for p 0.720.
To construct a confidence interval for the population proportion use the normal approximation to the binomial distribution when the sample size is large (n > 30) and the success-failure condition is met (np > 5 and n(1 - p) > 5).
n = 400 and E(x) = 288. To calculate the confidence interval follow these steps:
Calculate the sample proportion:
P = E(x) / n = 288 / 400 = 0.72
Calculate the standard error:
SE = √(P(1 - P) / n) = √((0.72 × 0.28) / 400) ≈ 0.025
Determine the critical value corresponding to a 90% confidence level. Since the distribution is approximately normal use the Z-distribution. The critical value for a 90% confidence level is approximately 1.645.
Calculate the margin of error:
ME = critical value × SE = 1.645 × 0.025 = 0.041
Construct the confidence interval:
Confidence Interval = P ± ME
= 0.72 ± 0.041
To know more about value here
https://brainly.com/question/30035551
#SPJ4
Need help asap please
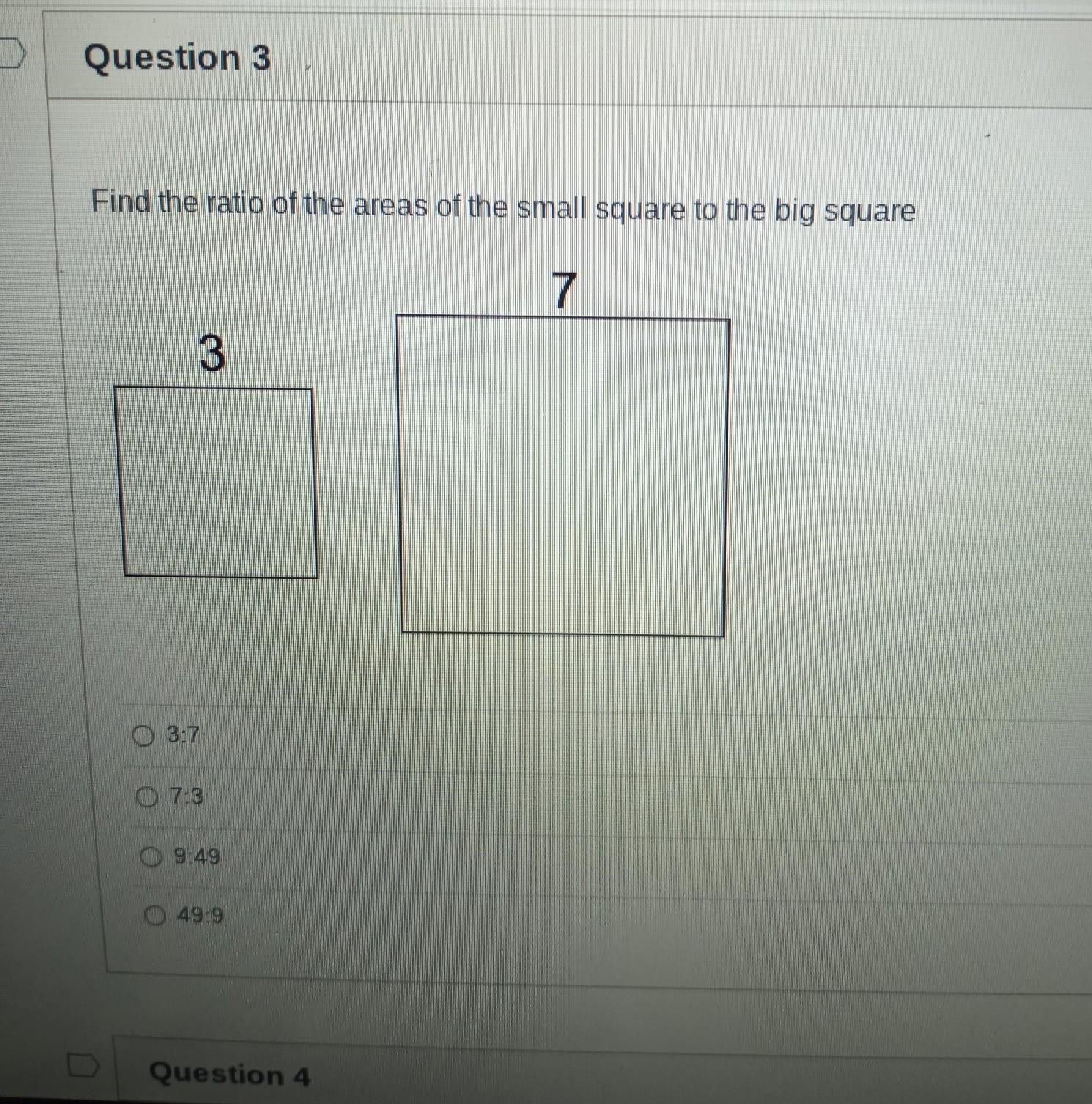
Answers
Answer:
9:49 is the answer because question say ratio is square of small and big
2.1 The sieve analysis results for an aggregate sample is displayed below. (a) Calculate the percentage passing for each sieve size
Answers
We determine the cumulative weight retained at each sieve and then calculate the cumulative percentage passing by dividing the cumulative weight passing by the total weight of the sample and multiplying by 100.
To calculate the percentage passing for each sieve size in a sieve analysis, we need to determine the cumulative percentage passing at each sieve size.
The sieve analysis provides information about the particle size distribution of an aggregate sample. It involves passing the sample through a series of sieves with different mesh sizes, and measuring the amount of material retained on each sieve.
To calculate the percentage passing, we first need to determine the cumulative weight retained at each sieve size. This is done by subtracting the weight retained on a particular sieve from the weight retained on the previous sieve.
Once we have the cumulative weight retained, we can calculate the cumulative percentage passing by dividing the cumulative weight passing by the total weight of the sample and multiplying by 100.
Here is an example:
Sieve Size (mm) | Weight Retained (g)
4.75 | 50
2.36 | 30
1.18 | 20
0.6 | 15
0.3 | 10
0.15 | 5
To calculate the cumulative percentage passing:
Calculate the cumulative weight retained:
Cumulative weight retained at sieve 4.75 mm = 50 g
Cumulative weight retained at sieve 2.36 mm = 50 g + 30 g = 80 g
Cumulative weight retained at sieve 1.18 mm = 80 g + 20 g = 100 g
Cumulative weight retained at sieve 0.6 mm = 100 g + 15 g = 115 g
Cumulative weight retained at sieve 0.3 mm = 115 g + 10 g = 125 g
Cumulative weight retained at sieve 0.15 mm = 125 g + 5 g = 130 g
Calculate the cumulative percentage passing:
Cumulative percentage passing at sieve 4.75 mm = (Total weight - Cumulative weight retained) / Total weight * 100 = (130 g - 50 g) / 130 g * 100 = 61.54%
Cumulative percentage passing at sieve 2.36 mm = (130 g - 80 g) / 130 g * 100 = 38.46%
Cumulative percentage passing at sieve 1.18 mm = (130 g - 100 g) / 130 g * 100 = 23.08%
Cumulative percentage passing at sieve 0.6 mm = (130 g - 115 g) / 130 g * 100 = 11.54%
Cumulative percentage passing at sieve 0.3 mm = (130 g - 125 g) / 130 g * 100 = 3.85%
Cumulative percentage passing at sieve 0.15 mm = (130 g - 130 g) / 130 g * 100 = 0%
Learn more about distribution here:
https://brainly.com/question/29664127
#SPJ11
