nilai x yang memenuhi |3x + 7| > 2 adalah....
Answers
Answer:
|3x+7|>2 =5/3 x yang memenuhi
Related Questions
List the first five terms of the sequence: \[ a_{1}=27 \quad d=-5 \]
Answers
The first five terms of the sequence are 27, 22, 17, 12, and 7.
To find the first five terms of the sequence given by a₁=27 and d=-5,
we can use the formula for the nth term of an arithmetic sequence:
\(a_n=a_1+(n-1)d\)
Substituting the given values, we have:
\(a_n=27+(n-1)(-5)\)
Now, we can calculate the first five terms of the sequence by substituting the values of n from 1 to 5:
\(a_1=27+(1-1)(-5)=27\)
\(a_1=27+(2-1)(-5)=22\)
\(a_1=27+(3-1)(-5)=17\)
\(a_1=27+(4-1)(-5)=12\)
\(a_1=27+(5-1)(-5)=7\)
Therefore, the first five terms of the sequence are 27, 22, 17, 12, and 7.
To learn more about sequence visit:
brainly.com/question/23857849
#SPJ11
Find the measure of the three angles in triangle LMN based on the information given below, and then answer the next two questions (Hint:apply thereom 10-A) m

Answers
Find the measure of the three angles in triangle LMN based on the information given below, and then answer the next two questions (Hint: apply thereom 10-A)
m∠L=7x+2
m∠M=3x-7
m∠N=5x-10
1)What is (a) the value of "x",
(b) the measure of angle L
(c) the measure of angle M
(d) the measure of angle N
___________________________________
The sum of the internal angles of a triangle is 180
m∠L + m∠M + m∠N = 180º
7x+2 + 3x-7 + 5x-10 = 180º
(7+3+5)x = 180º- (2-7-10)
15 x = 180º - (-15)
15 x = 180º + 15
x= 195/15
x= 13
___________________
Answer
x= 13
m∠L= 7x + 2 = 7*(13) + 2 = 93º
m∠M= 3x - 7 = 3*(13) - 7 =32º
m∠N= 5x - 10 = 5(13)- 10= 55º
______________________
Organizing the angles from largest to smallest
m∠L > m∠N > m∠M
_____________________

Simplify the fraction 2/18
9/1
1/6
6/1
1/9
Answers
Answer:
27/2
,
12/1
9/1
Step-by-step explanation:18
1
9
2
,
6
1
6
1
,
9
1
2 Simplify 18\frac{9}{1}18
1
9
to 18+918+9.
\frac{2}{18+9},\frac{1}{6\frac{6}{1}},\frac{1}{9}
18+9
2
,
6
1
6
1
,
9
1
3 Simplify 18+918+9 to 2727.
\frac{2}{27},\frac{1}{6\frac{6}{1}},\frac{1}{9}
27
2
,
6
1
6
1
,
9
1
4 Simplify \frac{6}{1}
1
6
to 66.
\frac{2}{27},\frac{1}{6\frac{6}{1}},\frac{1}{9}
27
2
,
6
1
6
1
,
9
1
5 Simplify 6\frac{6}{1}6
1
6
to 6+66+6.
\frac{2}{27},\frac{1}{6+6},\frac{1}{9}
27
2
,
6+6
1
,
9
1
You have an equally likely chance of choosing any integer from 1 through 50. Find the probability of the given event. A perfect square is chosen.
Answers
Answer:
The answer is 0.02
Step-by-step explanation:
1/50=0.02
hellp please this is math grade 10

Answers
Answer:
16. real number, rational number, integer
17. real number, rational, integer
18. whole number, real number, integer, rational
19. whole, real, integer, rational
20. irrational
21. rational, real, whole, integer
Step-by-step explanation:
What's additive property
Answers
The additive property of equality states that if the same amount is added to both sides of an equation, then the equality is still true.
Help for Financial algebra problem!
Close up on the fractions:
7/e - 1/2 =5/e

Answers

Evaluate the following expression:

Answers
Answer:
11x
Step-by-step explanation:
(8.1 + 7.9)x - (25 / 5)x
16x - 5x
11x
Why?
(8.1+7.9)x-(25/5)x
First add 8.1 and 7.9 and get 16
Then 25/5 and you get 5 so after that you have
16x-5x so 11x is the answer
What is the measure of 23 if clld?

Answers
Answer:
i tink im doing this complete wrong but 1.380649×10−23 J
Step-by-step explanation:
hiii please help! i’ll give brainliest if you give a correct answer tysm!

Answers
Answer: 3/16
Step-by-step explanation:
Reduce the expression, if possible, by cancelling the common factors.
Select all of the following statements that are true.
All real numbers are natural numbers.
All whole numbers are integers.
All integers are whole numbers.
All natural numbers are rational numbers.
All irrational numbers are dense.
DONE
Answers
Answer:
All whole numbers are integer
All natural numbers are rational numbers
Step-by-step explanation:
Answer:
2, 4, 5
Step-by-step explanation:
edge 2021 :)
please help me with this its math!!
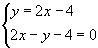
Answers
If this doesn’t look right, then I need you to tell me what kind of method you use to solve this then I will help more.
big ideas integrated 1 chapter 8 test? anyone ?
Answers
Answer:
Uh, sure! :)
Step-by-step explanation:
n2 + n = 56 solution
Answers
Answer:
n = -8, 7
Step-by-step explanation:
Your equation is:
\(\displaystyle{n^2+n=56}\)
Arrange the terms in the quadratic expression, ax² + bx + c:
\(\displaystyle{n^2+n-56=0}\)
Factor the expression, thus:
\(\displaystyle{\left(n+8\right)\left(n-7\right)=0}\)
This is because 8n-7n = n (middle term) and 8(-7) = -56 (last term). Then solve like a linear which results in:
\(\displaystyle{n=-8,7}\)
Hello!
\(\sf n^2 + n = 56\\\\n^2 + n - 56 = 0\\\\\\n = \dfrac{-b\±\sqrt{b^2-4ac} }{2a} \\\\\\n = \dfrac{-1\±\sqrt{1^2-4*1*(-56)} }{2*1}\\\\\\n = \dfrac{1\±15}{2} \\\\\\\boxed{\sf n = 7 ~or ~-8 }\)
This trip the family will spend $117.96. The next trip they will spend $119.27. This is an increase of ($117.96 − $119.27) or an increase of $1.31. What is the percent of increase? Round your answer to the nearest whole percent.
Answers
Answer:
1%
Step-by-step explanation:
To find the percent increase, take the difference over the original amount
1.31/ 117.96
.011105459
Change to percent form
1.110545948%
To the nearest percent
1%
a 150 ft tree casts a shadow of 225 ft how many feet tall is a nearby tree that casts a 75 ft shadow at the same time
Answers
Consider that both trees and their shadows for two right triangles.
These triangles are similar, then, the proportion between similar sides must be equal.
The proportion between the tall of the trees is equal to the prportion to the length of their shadows. If x is the tall of the tree with the shadow os 75 ft, you have:
x/225 = 75/150
solve the previous equation for x:
x = (75/150)(225)
x = 112.5
Hence, the tall of the tree is 112.5 ft
What is the area of a rectangle with a length of 9 feet and a width of 7 grade
Answers
9 x 7 = 63 feet
Answer:
63
Step-by-step explanation:
area=length×width so 9×7=63
For each of the functions given below, use Newton's method to approximate all real roots. Use an absolute tolerance of 10^−6
as a stopping condition. (a) f(x)=e^x+x^2−x−4 (b) f(x)=x^3−x^2−10x+7 (c) f(x)=1.05−1.04x+lnx
Answers
(a) The approximated root of f(x) = e^x + x^2 - x - 4 is x ≈ 2.151586.
(b) The approximated root of f(x) = x^3 - x^2 - 10x + 7 is x ≈ -0.662460.
(c) The approximated root of f(x) = 1.05 - 1.04x + ln(x) is x ≈ -1.240567.
(a) Purpose: f(x) = ex + x2 - x - 4 To apply Newton's method, we must determine the function's derivative as follows: f'(x) = e^x + 2x - 1.
Now, we can use the formula to iterate: Choose an initial guess, x(0) = 0, and carry out the iterations as follows: x(n+1) = x(n) - f(x(n))/f'(x(n)).
1. Iteration:
Iteration 2: x(1) = 0 - (e0 + 02 - 0 - 4) / (e0 + 2*0 - 1) = -4 / (-1) = 4.
2.229280 Iteration 3: x(2) = 4 - (e4 + 42 - 4 - 4) / (e4 + 2*4 - 1)
x(3) 2.151613 The Fourth Iteration:
x(4) 2.151586 The Fifth Iteration:
x(5) 2.151586 The equation f(x) = ex + x2 - x - 4 has an approximate root of x 2.151586.
(b) Capability: f(x) = x3 - x2 - 10x + 7 The function's derivative is as follows: f'(x) = 3x^2 - 2x - 10.
Let's apply Newton's method with an initial guess of x(0) = 0:
1. Iteration:
x(1) = 0 - (0,3 - 0,2 - 100 + 7), or 7 / (-10) -0.7 in Iteration 2.
x(2) -0.662500 The Third Iteration:
x(3) -0.662460 The fourth iteration:
The approximate root of the equation f(x) = x3 - x2 - 10x + 7 is x -0.662460, which is x(4) -0.662460.
c) Purpose: f(x) = 1.05 - 1.04x + ln(x) The function's derivative is as follows: f'(x) = -1.04 + 1/x.
Let's use Newton's method to make an initial guess, x(0) = 1, and choose:
z
1. Iteration:
x(1) = 1 - (1.05 - 1.04*1 + ln(1))/(- 1.04 + 1/1)
= 0.05/(- 0.04)
≈ -1.25
Cycle 2:
x(2) less than -1.240560 Iteration 3:
x(3) less than -1.240567 Iteration 4:
x(4) -1.240567 The equation f(x) = 1.05 - 1.04x + ln(x) has an approximate root of x -1.240567.
To know more about Root, visit
brainly.com/question/428672
#SPJ11
Sophia pays a $19.99 membership fee for an online music store. If Sophia purchases n songs for $0.99 each, write an expression for the total cost.
Part B
If she buys two songs from a new album, what is the total cost?
Answers
Answer:
19.99+n0.99
B:
19.99+0.99+0.99=
21.97
hope this all helps!!!
What is the probability that a passenger prefers to sit in front of the plane and prefers a window seat

Answers
Answer:
A
Step-by-step explanation:
This is a probability question.
We want to calculate the probability that a passenger prefers to sit in front of the plane and at a window seat.
The answer here is directly obtainable from the table. Let’s take a look at that point where we have the front and window merging. We can see that the figure here is 8
Thus, the probability that we want to calculate is this figure over the total = 8/36
= 2/9
E15 gasoline contains 15% of alcohol calculate the volume in liters of alcohol in a full 20 gallon gas tank
Answers
Since, 1 gallon = 3.78541 liters
Therefore, 20 gallons = 75.7082 liters
That means amount of gasoline in the gas tank is 20 gallons or 75.7082 liters.
It's given in the question that E15 gasoline contains 15% of alcohol.
Therefore, amount of alcohol in the gas tank = 15% of 75.7082
= 11.35623
≈ 11.36 liters
Learn more,
https://brainly.com/question/618776
Amount of total Alcohol in liters is 11.355 liter.
Given:
Amount of total gas solution = 20 gallon
Amount of Alcohol in total gas = 15%
Find:
Amount of total Alcohol in liters
Computation:
1 Gallon = 3.785 liter (Approx.)
Amount of total gas solution in liter = 20 × 3.785
Amount of total gas solution in liter = 75.7 liter (Approx.)
Amount of total Alcohol in liters = Amount of total gas solution in liter × Amount of Alcohol in total gas
Amount of total Alcohol in liters = 75.7 × 15%
Amount of total Alcohol in liters = 75.7 × 0.15
Amount of total Alcohol in liters = 11.355 liter (Approx.)
Learn more:
https://brainly.com/question/1578538?referrer=searchResults
use the theorem given below to find the curvature. r(t) = 9t i 4 sin(t) j 4 cos(t) k theorem: the curvature of the curve given by the vector function r is (t) = |r ′(t) ⨯ r″(t)| |r ′(t)|3 .
Answers
To find the curvature of the curve represented by the vector function \(r(t) = 9t \mathbf{i} + 4 \sin(t) \mathbf{j} + 4 \cos(t) \mathbf{k}\), we can use the given theorem:
The curvature (\(k(t)\)) of a curve defined by the vector function \(r(t)\) is given by the formula \(k(t) = \left|\frac{{\mathbf{r}'(t) \times \mathbf{r}''(t)}}{{\left|\mathbf{r}'(t)\right|^3}}\right|\).
First, we need to find the first and second derivatives of \(r(t)\):
\(\mathbf{r}'(t) = 9 \mathbf{i} + 4 \cos(t) \mathbf{j} - 4 \sin(t) \mathbf{k}\)
\(\mathbf{r}''(t) = -4 \sin(t) \mathbf{j} - 4 \cos(t) \mathbf{k}\)
Next, we substitute these derivatives into the formula for curvature:
\(k(t) = \left|\frac{{(9 \mathbf{i} + 4 \cos(t) \mathbf{j} - 4 \sin(t) \mathbf{k}) \times (-4 \sin(t) \mathbf{j} - 4 \cos(t) \mathbf{k})}}{{\left|(9 \mathbf{i} + 4 \cos(t) \mathbf{j} - 4 \sin(t) \mathbf{k})\right|^3}}\right|\)
Simplifying this expression involves calculating the cross product, magnitude, and simplification of terms. However, without further information about the range of \(t\) or specific values, it is challenging to provide a specific numerical answer.
The curvature of a curve represents the rate at which the curve deviates from being a straight line at any given point. It describes how sharply the curve bends or curves at that point. In this case, the vector function \(r(t)\) describes a three-dimensional curve in space. By calculating the curvature using the given theorem, we can determine how the curve bends or curves at different values of \(t\).
The curvature can provide insights into the geometry and behavior of the curve. For example, if the curvature is large, it indicates a sharp bend or curve, while a small curvature suggests a relatively straight or gently curving segment. By analyzing the curvature at various points along the curve, we can identify regions of significant curvature, such as points of inflection or areas with high curvature. This information is valuable in fields such as physics, engineering, computer graphics, and geometry, where understanding the shape and behavior of curves is essential.
know more about curvature of the curve :brainly.com/question/32215102
#SPJ11
The curvature of the curve given by the vector function r(t) = 9t i + 4sin(t) j + 4cos(t) k is (4/97) * sqrt(1296sin^2(t) + 256cos^4(t)).
To find the curvature of the curve given by the vector function r(t) = 9t i + 4sin(t) j + 4cos(t) k using the provided theorem, we need to compute the first and second derivatives of r(t) and then apply the formula for curvature.
First, let's find the first derivative, r'(t), of the vector function r(t):
r'(t) = (d/dt)(9t i + 4sin(t) j + 4cos(t) k)
= 9 i + 4cos(t) j - 4sin(t) k
Next, let's find the second derivative, r''(t), by differentiating r'(t):
r''(t) = (d/dt)(9 i + 4cos(t) j - 4sin(t) k)
= -4sin(t) j - 4cos(t) k
Now, we can calculate the cross product of r'(t) and r''(t):
r'(t) ⨯ r''(t) = (9 i + 4cos(t) j - 4sin(t) k) ⨯ (-4sin(t) j - 4cos(t) k)
Using the properties of the cross product, we can expand this expression:
r'(t) ⨯ r''(t) = (9 * (-4sin(t))) i ⨯ j
+ (9 * (-4sin(t))) i ⨯ k
+ (4cos(t) * (-4cos(t))) j ⨯ k
Simplifying further:
r'(t) ⨯ r''(t) = -36sin(t) i
- 36sin(t) k
- 16cos^2(t) j
Now, let's calculate the magnitude of r'(t) ⨯ r''(t):
|r'(t) ⨯ r''(t)| = sqrt((-36sin(t))^2 + (-36sin(t))^2 + (-16cos^2(t))^2)
= sqrt(1296sin^2(t) + 256cos^4(t))
Next, we need to compute the magnitude of r'(t):
|r'(t)| = sqrt((9)^2 + (4cos(t))^2 + (-4sin(t))^2)
= sqrt(81 + 16cos^2(t) + 16sin^2(t))
= sqrt(81 + 16)
|r'(t)| = sqrt(97)
Finally, we can plug these values into the formula for curvature:
k(t) = |r'(t) ⨯ r''(t)| / |r'(t)|^3
= sqrt(1296sin^2(t) + 256cos^4(t)) / (sqrt(97))^3
Simplifying further:
k(t) = (4/97) * sqrt(1296sin^2(t) + 256cos^4(t))
Therefore, the curvature of the curve given by the vector function r(t) = 9t i + 4sin(t) j + 4cos(t) k is (4/97) * sqrt(1296sin^2(t) + 256cos^4(t)).
know more about curvature of the curve :brainly.com/question/32215102
#SPJ11
Name the property illustrated by if a = -3 and -3 = b, then a = b.
Answers
The Transitive property states that;
if a=b and b=c then a=c.
and c by b.
if a = -3 and -3 = b, then a = b.
So, the property illustrated is similar to the Transitive property
Therefore, the property illustrated is the Transitive property.So, if you replace b with -3 we have;
f
–
4
1
2
?
–
1.5 what symblol do i put
Answers
Answer What does 1.5 mean on a number?
If a half = 0.5 and one =1, than one and a half is 1+0.5=1.5. So, 1.5 = one and a half.
Step-by-step explanation:
A jar has 10 red marbles, 6 purple marbles, and 4 turquoise marbles. Grace wins if she selects at turquoise marble from the jar. Is this game fair
Answers
In the above-given situation of Grace (C) No, the game is not fair because Grace has a higher probability of choosing a marble of another color.
What is probability?Probability is a branch of mathematics that deals with numerical descriptions of how likely an event is to occur or how likely a proposition is to be true. The probability of an event is a number between 0 and 1, where 0 indicates the event's impossibility and 1 indicates certainty.A probability formula can be used to calculate the probability of an event by simply dividing the favorable number of outcomes by the total number of possible outcomes.To find whether the above-given situation is fair or not:
A fair game is one in which the expected average payout is equal to zero. If a win equals one and a loss equals one, we can establish a relationship by multiplying these payouts by their probabilities.So, 1(4/20) + -1(16/20) = ?This relationship should equal 0 if this were a fair game. However, we notice that the final value is -12/20 or -3/5. This demonstrates that her average payout is significantly less than 0.Therefore, in the above-given situation of Grace (C) No, the game is not fair because Grace has a higher probability of choosing a marble of another color.
Know more about probability here:
https://brainly.com/question/24756209
#SPJ4
The correct question is given below:
A jar has 10 red marbles, 6 purple marbles, and 4 turquoise marbles. Grace wins if she selects a turquoise marble from the jar. Is this game fair? Why or why not?
(A) Yes, the game is fair because Grace has equal probabilities of choosing a marble of either color.
(B) Yes, the game is fair because Grace has equal probabilities of winning and losing.
(C) No, the game is not fair because Grace has a higher probability of choosing a marble of another color.
(D) No, the game is not fair because Grace has equal probabilities of winning and losing
The point given below is on the terminal side of an angle θ in standard position. Find the exact value of each of the six trigonometric functions of θ. (8,−6)
Answers
In order to find the exact values of the six trigonometric functions of the given angle θ, we will first have to find the values of the three sides of the right triangle formed by the given point (8, -6) and the origin (0, 0).
Let's begin by plotting the point on the Cartesian plane below:From the graph, we can see that the point (8, -6) lies in the fourth quadrant, which means that the angle θ is greater than 270 degrees but less than 360 degrees. The distance from the origin to the point (8, -6) is the hypotenuse of the right triangle formed by the point and the origin. We can use the distance formula to find the length of the hypotenuse:hypotenuse = √(8² + (-6)²) = √(64 + 36) = √100 = 10Now we can find the lengths of the adjacent and opposite sides of the triangle using the coordinates of the point (8, -6):adjacent = 8opposite = -6Now we can use these values to find the exact values of the six trigonometric functions of θ:sin θ = opposite/hypotenuse = -6/10 = -3/5cos θ = adjacent/hypotenuse = 8/10 = 4/5tan θ = opposite/adjacent = -6/8 = -3/4csc θ = hypotenuse/opposite = 10/-6 = -5/3sec θ = hypotenuse/adjacent = 10/8 = 5/4cot θ = adjacent/opposite = 8/-6 = -4/3Therefore, the exact values of the six trigonometric functions of θ are:sin θ = -3/5cos θ = 4/5tan θ = -3/4csc θ = -5/3sec θ = 5/4cot θ = -4/3
To know more about trigonometric functions, visit:
https://brainly.com/question/25618616
#SPJ
1.4. The price of a Grade 4 mathematics textbook is discounted by 15%. The old price was R350,00. Calculate the discount price. (3)
Answers
The discounted price of the Grade 4 mathematics textbook after a 15% discount is R297.50.
To calculate the discount price, we first need to determine the discount amount. We multiply the original price by the discount percentage: R350.00 * 0.15 = R52.50.
Next, we subtract the discount amount from the original price to find the discounted price: R350.00 - R52.50 = R297.50.
Therefore, the discount price of the Grade 4 mathematics textbook is R297.50.
Learn more about Discount here
https://brainly.com/question/13501493
#SPJ11
A pizza maker determined an annual profit in dollars
2
from selling pizzas using f(n) = 65n -0.04n² where
n is the number of pizzas sold. What is the annual
profit if the pizza maker sells 300 pizzas?
A. $18,500
B. $3,600
C. $7,800
D. $15,900
Answers
Answer:
Given, the annual profit equation is f(n) = 65n - 0.04n².
When the number of pizzas sold, n = 300, the annual profit will be:
f(300) = 65(300) - 0.04(300)²
= 19500 - 0.04(90000)
= 19500 - 3600
= $15,900
Therefore, the annual profit if the pizza maker sells 300 pizzas is $15,900. Answer: D.
Step-by-step explanation:
Use the given equation to answer the following questions. y 2
−x 2
=16 (a) Find the vertices, foci, and asymptotes of the hyperbola. (Enter your answers from smallest to largest.) (i) vertices (,) (smaller y-value) (, ) (larger y-value) (ii) foci (,) (smaller y-value) (, ) (larger y-value) (ii) asymptotes y= (smaller slope) y= (larger slope)
Answers
The vertices of the hyperbola are (-4, 0) and (4, 0), the foci are (-5, 0) and (5, 0), and the asymptotes are y = -x and y = x.
The equation of the given hyperbola is in the standard form\(\(\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\), where \(a\) represents the distance from the center to the vertices and \(c\) represents the distance from the center to the foci. In this case, since the coefficient of \(y^2\)\)is positive, the transverse axis is along the y-axis.
Comparing the given equation with the standard form, we can determine that \(a^2 = 16\) and \(b^2 = -16\) (since \(a^2 - b^2 = 16\)). Taking the square root of both sides, we find that \(a = 4\) and \(b = \sqrt{-16}\), which simplifies to \(b = 4i\).
Since \(b\) is imaginary, the hyperbola does not have real asymptotes. Instead, it has conjugate asymptotes given by the equations y = -x and y = x.
The center of the hyperbola is at the origin (0, 0), and the vertices are located at (-4, 0) and (4, 0) on the x-axis. The foci are found by calculating \(c\) using the formula \(c = \sqrt{a^2 + b^2}\), where \(c\) represents the distance from the center to the foci. Plugging in the values, we find that \(c = \sqrt{16 + 16i^2} = \sqrt{32} = 4\sqrt{2}\). Therefore, the foci are located at (-4\sqrt{2}, 0) and (4\sqrt{2}, 0) on the x-axis.
In summary, the vertices of the hyperbola are (-4, 0) and (4, 0), the foci are (-4\sqrt{2}, 0) and (4\sqrt{2}, 0), and the asymptotes are y = -x and y = x.
learn more about hyperbola here
https://brainly.com/question/19989302
#SPJ11
solve the equation 2x-11=k for x
Answers
x = k/2 + 11/2
Step-by-step explanation:
\(\frac{k}{2} + \frac{11}{2} = \frac{k+11}{2}\)
hope this helped :)