On a number line, the ordinate of point K is 25 and the ordinate of point D is -84. What is the length of KD
Answers
=======================================================
Explanation:
Draw out a number line. Plot point D at -84 and K at 25. Plot a third point, say point A, at 0.
From D to A is 84 units
From A to K is 25 units
Those two distances add to 84+25 = 109 units total, which is the distance from K to D on a number line. This is the same as the length of segment KD.
-----------
You could also show your steps like this
|D - K| = |-84 - 25| = |-109| = 109
The absolute value is to ensure the result is never negative.
The D and K can swap like so
|K - D| = |25 - (-84)| = |25+84| = |109| = 109
Either way we get the same distance.
Related Questions
L is the circle with the equation x²+y²=9
full question in photo :)

Answers
The values of the variables, a, b, and c obtained from the equation of the circle and the coordinates of the point P are;
a) a = 2
b = -2
c = 4
What is the general equation of a circle?The general equation of a circle is; (x - h)² + (y - k)² = r²
Where;
(h, k) = The coordinates of the center of the circle
r = The coordinates of the radius of the circle
The specified equation of a circle is; x² + y² = 9
The coordinates of the center of the circle, is therefore, O = (0, 0)
a) The coordinates of the points P and O indicates that the gradient of OP, obtained using the slope formula is; ((3·√3)/4 - 0)/(3/2 - 0) = ((3·√3)/4)/(3/2)
((3·√3)/4)/(3/2) = (√3)/2
The specified form of the gradient is; (√3)/a, therefore;
(√3)/a = (√3)/2
a = 2
The value of a is 2
b) The gradient of the tangent to a line that has a gradient of m is -1/m
The gradient of OP is; (√3)/2, therefore, the gradient of the tangent at P is -2/(√3)
The form of the gradient of the tangent at P is b/(√3), therefore;
-2/(√3) = b/(√3)
b = -2
The value of b is; -2
c) The coordinate of the point on the tangent, (0, (7·√3)/c) indicates
Slope of the tangent = -2/(√3)
((7·√3)/c - ((3·√3)/4))/(0 - (3/2)) = -2/(√3)
((7·√3)/c - ((3·√3)/4)) = (3/2) × 2/(√3) = √3
(7·√3)/c = √3 + ((3·√3)/4) = 7·√3/4
Therefore; c = 4
Learn more on the equation of a circle here: https://brainly.com/question/12182614
#SPJ1
Is the function f(x)=
–
2
7
+
1
8x
linear or nonlinear?
Answers
Answer:
as long as the equation has no exponents or square roots it is linear
Step-by-step explanation:
Let A={(x-3)/(x-2)ЄR : X<0}
be a subset of real numbers.
i) Define A's supremum and infimum.
Answers
The supremum of the set A does not exist (it is negative infinity), and the infimum of the set A is 1.
To define the supremum and infimum of the set A, we first need to determine the properties of the set.
The set A is defined as A = {(x-3)/(x-2) ∈ R : x < 0}.
To find the supremum (also known as the least upper bound) of A, we need to find the smallest value that is greater than or equal to all the elements of A. In other words, we are looking for the least upper bound of the set A.
Let's analyze the elements of A:
For x < 0, the expression (x-3)/(x-2) can take on different values depending on the value of x. We need to find the maximum value that this expression can reach for all x < 0.
As x approaches 0 from the left side, (x-3)/(x-2) approaches negative infinity. Therefore, there is no finite supremum for the set A.
Next, let's find the infimum (also known as the greatest lower bound) of A. We need to find the largest value that is less than or equal to all the elements of A. In other words, we are looking for the greatest lower bound of the set A.
Again, analyzing the elements of A:
As x approaches negative infinity, (x-3)/(x-2) approaches 1. Therefore, the infimum of the set A is 1.
For more such questions on supremum visit;
https://brainly.com/question/33059731
#SPJ8
the weights of oranges growing in an orchard are normally distributed with a mean weight of 8 oz. and a standard deviation of 2 oz. from a batch of 1400 oranges, how many would be expected to weigh more than 4 oz. to the nearest whole number? 1) 970 2) 32 3) 1368 4) 1295
Answers
The number of oranges that are expected to weigh more than 4 oz is:
1400 - (1400 × 0.0228)≈ 1368.
The mean weight of the oranges growing in an orchard is 8 oz and standard deviation is 2 oz, the distribution of the weight of oranges can be represented as normal distribution.
From the batch of 1400 oranges, the number of oranges is expected to weigh more than 4 oz can be found using the formula for the Z-score of a given data point.
\(z = (x - μ) / σ\)
Wherez is the Z-score of the given data point x is the data point
μ is the mean weight of the oranges
σ is the standard deviation
Now, let's plug in the given values.
\(z = (4 - 8) / 2= -2\)
The area under the standard normal distribution curve to the left of a Z-score of -2 can be found using the standard normal distribution table. It is 0.0228. This means that 0.0228 of the oranges in the batch are expected to weigh less than 4 oz.
To know more about normal distribution visit :
https://brainly.com/question/23418254
#SPJ11
Verify the identity.
(cos x/1 + sin x) = sec x - tan x
Drag an expression into each box to correctly complete the verification of the identity.
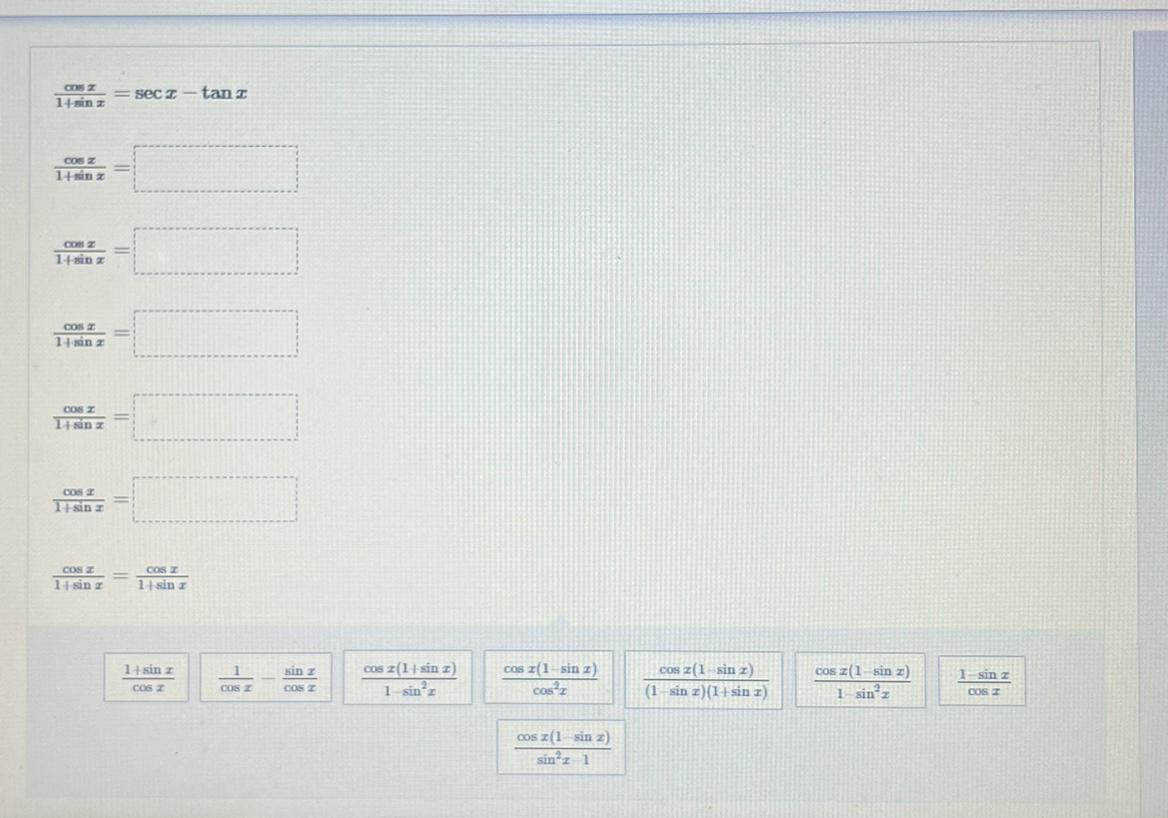
Answers
Answer:
this are the answers
Step-by-step explanation:

The trigonometric value identity is solved (cos x/1 + sin x) = sec x - tan x
What are trigonometric relations?Trigonometry is the study of the relationships between the angles and the lengths of the sides of triangles
The six trigonometric functions are sin , cos , tan , cosec , sec and cot
Let the angle be θ , such that
sin θ = opposite / hypotenuse
cos θ = adjacent / hypotenuse
tan θ = opposite / adjacent
tan θ = sin θ / cos θ
cosec θ = 1/sin θ
sec θ = 1/cos θ
cot θ = 1/tan θ
Given data ,
To verify the identity (cos x / (1 + sin x)) = sec x - tan x, we need to simplify the right-hand side of the equation using trigonometric identities and see if it matches the left-hand side.
sec x - tan x = 1/cos x - sin x/cos x = (1 - sin x)/cos x
On simplifying , we get
cos x / (1 + sin x) = cos x / (1 + sin x) * (1 - sin x)/(1 - sin x) = cos x * (1 - sin x) / (1 - sin²x)
Using the Pythagorean identity sin²x + cos² x = 1, we can substitute 1 - cos²x for sin²x in the denominator:
So , cos x / (1 + sin x) = cos x ( 1 + sin x ) / cos²x
On further simplification , we get
cos x / (1 + sin x) = cos x / cos²x + cos x ( sin x ) / cos²x
cos x / (1 + sin x) = ( 1/cos x ) + ( sin x / cos x )
From the trigonometric relations , we get
cos x / (1 + sin x) = sec x - tan x
Hence , the trigonometric equation is solved
To learn more about trigonometric relations click :
https://brainly.com/question/14746686
#SPJ2
Does the number line below represent the solution to the inequality x > -2?

Answers
Answer:
B I aplogize if its wrong i haven't done this type of math in a couple years so its foggy
Hope it Helps!
Solve for s.
(6s - 5)(s - 3) = 0
Write your answers as integers or as proper or improper fractions in simplest form.
S = or s =
Answers
Answer:
s = 5/6, s = 3
Step-by-step explanation:
(6s - 5)(s - 3) = 0
Solving for s:
1. ...........
6s - 5 =06s = 5s = 5/62. ...........
s - 3 = 0s =3Use 45-45-90 & 30-60-90 Special Right Triangles to Solve. find the missing sir length. Leave you answers as radicals in simplest form

Answers
Answer:5) x=y=7×6^1/2,6)x=38,y=19×3^1/2
7)m=n=18,8)u= 2×5^1/2,v=3
Step-by-step explanation: use trigonometry laws
Jose is planning to drive from New York City to Dallas in his car. Jose was curious and started to complete the table shown to indicate how far in mles he can travel for each gallon of gas he uses
How far did Jose travel with 10 gallons of gas?
Answers
Answer:
200 miles
Step-by-step explanation:
you travel 20 miles for 1 gallon, so 10*20=200miles
Answer:
200
Step-by-step explanation:
if you have to dive its 20 times 10 because 20 miles 10 dollars
8. player 1 runs to first base at a speed of 20 ft/s while player 2 runs from second base to third base at a speed of 15 ft/s. let s be the distance between the two players. how fast is s changing when player 1 is 30 ft from home plate and player 2 is 60 ft from second base?
Answers
In linear equation, 90 ft is the distance between the two players .
What in mathematics is a linear equation?
A linear equation is a first-order (linear) term plus a constant in the algebraic form y=mx+b, where m is the slope and b is the y-intercept.Sometimes, the aforementioned is referred to as a "linear equation of two variables," where x and y are the variables.Let player 1 distance from home plate = x ft
so, dx/dt = 20 ft/sec
let player 2 distance from 2nd base = y ft
dy/dt = 15 ft/sec
we know that baseball around is of square type with length 90 ft .
we have to find change in s.
x = 40 ft , y = 50 ft
applying Pythagoras .
S² = (90)² + ( 90 - ( x + y ) )²
S² = ( 90)² + ( 90 - ( 50 + 40 ))²
S² = 90²
S = 90
Learn more about linear equation
brainly.com/question/11897796
#SPJ4
Given f(x) = (2 - x)}, what is the value of f(18)?
Answers
(2-18)
f(18)= -16
What is the value of x.

Answers
Answer:
19.8
Step-by-step explanation:
what is the value of -2|6x -y| when x-3 and y =4
Answers
So, we have been given the following
\(-2(6x -y)\)
But, we have also been given heads up that \(x=-3\), and \(y=4\).
So, that would mean the new equation would be the following.
\(-2(6-3 -4)\)
After we solve it our answer should be \(2\)!
If this helps then please mark me brainliest!
Answer:
-44Step-by-step explanation:
Given:
-2|6x -y|x = -3y = 4Solution:
-2|6*(-3) - 4| =-2|-22| =Absolute value is always positive, therefore |-22| = 22
-2*22 =-4410. What is the volume of a rectangular prism with the following dimensions: 5 in. x 2 3/4 in. x 10 1/2 in.? cubic inches
Answers
Answer:
144.375 or 144 3/8
Step-by-step explanation:
volume of rectangular prism= length x width x height
5in. x 2 3/4in. x 10 1/2 in. <- fractions can be converted to:
5in. x 2.75in. x 10.5 in. <- multiply and get:
= 144.375in.
in fraction form: 144 and 3/8
DRIVING Winston drove a total of 248 miles on Monday. He drove 70 fewer miles in the morning than he did in the afternoon. How many miles did he drive in the afternoon?
Answers
In the afternoon, Winston traveled a distance of 159 kilometers.
What is the distance?A mathematical number known as distance measures "how much ground an object has traveled" while moving. Distance is defined as the product of speed and time.
On Monday, Winston covered a distance of 248 miles. In the morning, he covered 70 fewer miles than in the afternoon.
Let "x" be the number of miles Winston drove in the afternoon.
In the morning, Winston drove x - 70 miles.
In total, Winston drove 248 miles on Monday.
So, x + (x - 70) = 248
2x - 70 = 248
2x = 318
x = 318/2
Apply the division operation, and we get
x = 159
Thus, Winston drove 159 miles in the afternoon.
Learn more about the distance here:
brainly.com/question/13269893
#SPJ1
PLEASEEEE HELP ASAPPPP
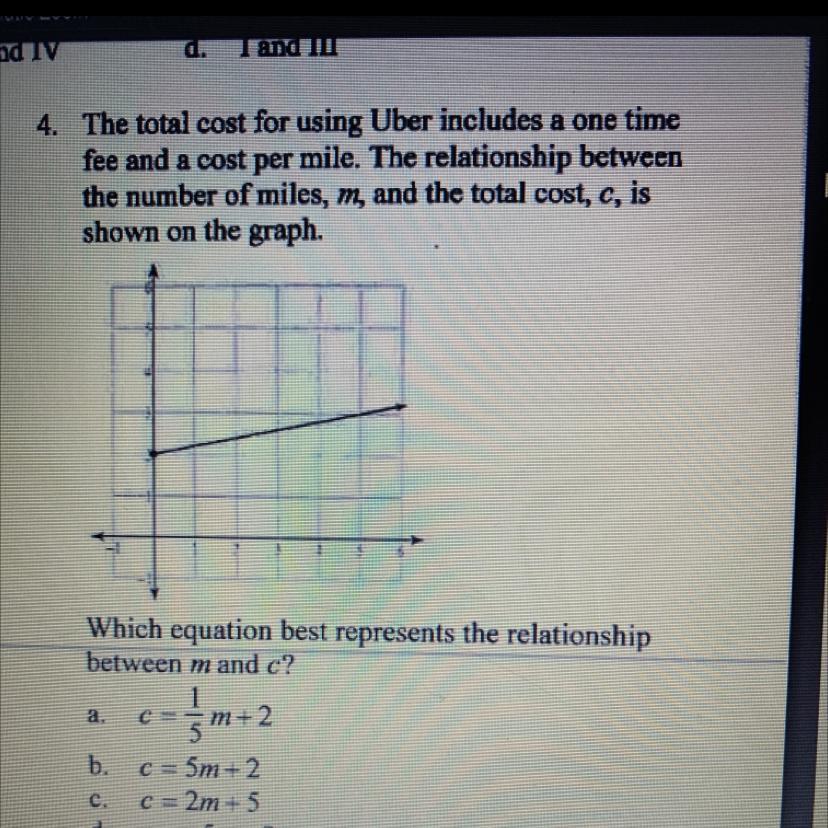
Answers
Answer:
I think its A
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
The y intercept is 2, visible on the graph.
The way I think about counting slope is (in this case)
"up one, over 5"
1/5
c=1/5m+2
D is your answer if there are 4 options (A, B, and C are incorrect; D isn't shown so I assume it's what I got)
HTH :)
Hosn is a picture framer. He is framing a picture that is 24 inches by 32 inches with a
frame that is 2.5 inches wide. What is the outer perimeter of the framed picture In yards, feet, and inches.
Answers
Answer: 122 sq. in.
Step-by-step explanation:
P = 2 (l + w)
P = 2 (34.5 + 26.5)
P = 2 x 61
P = 122 sq. in. = 0.847 sq ft = 0.0941 sq. yards
Perimeter is the sum of the side lengths of a shape. The outer perimeter of the framed picture is:
132 inches3.67 yard11 feetGiven that:
\(Length = 24in\\Width = 32in\)
The width of the frame is given as:
\(Frame =2.5in\)
So, the actual length and width of the framed picture is:
\(Length =24 + 2.5 + 2.5\)
\(Length =29in\)
\(Width = 32 + 2.5 + 2.5\)
\(Width = 37in\)
The outer perimeter (P) in inches is:
\(P= 2 \times (Length + Width)\)
So, we have:
\(P= 2 \times (29in + 37in)\)
\(P= 132in\)
The perimeter in yard, is as follows:
\(P= \frac{132}{36}yd\)
\(P = 3.67yd\)
The perimeter in feet is as follows:
\(P= \frac{132}{12}ft\)
\(P = 11ft\)
Hence, the outer perimeter of the frame is 132 inches
Read more about perimeters at:
https://brainly.com/question/6465134
a simple random sample of 5 observations from a population containing 400 elements was taken, and the following values were obtained. 12 18 19 20 21 a point estimate of the population mean is
Answers
A simple random sampling of 5 observations from a population containing 400 elements was taken. Then, the point estimate of the population means is 18.
You have a simple random sample of 5 observations from a population containing 400 elements, and the observed values are 12, 18, 19, 20, and 21.
To calculate the point estimate of the population mean, we simply take the average of the sample values.
Point estimate of population mean = (12 + 18 + 19 + 20 + 21)/5 = 18
Therefore, the point estimate of the population means is 18.
To clarify the terms used in the question, a "random sample" is a sample that is selected randomly from the population, meaning that every element in the population has an equal chance of being included in the sample. In this case, a simple random sample of 5 observations was taken. "Elements" refers to the individual units or objects within the population that is being studied. In this case, there were 400 elements in the population.
Learn more about Random Sampling:
brainly.com/question/29357010
#SPJ11
Find the missing side length, k.

Answers
Step-by-step explanation:
by using pythagorean theorema²+b²=c²a & c are given
to find k, let us use k as b
c²- a²=k²41²- 9²=k²1681-81=1600✓1600=40The two bases of a right conical frustum have radii 12 and 9. The two bases are 4 units apart. Let the volume of the frustum be $V$ cubic units and the total surface area of the frustum be $A$ square units. Find $V A$.
Answers
The product of the volume and total surface area of the given right conical frustum is approximately 146520π². To find the product of the volume and total surface area of a right conical frustum, we first need to determine the individual values of volume and surface area.
The volume of a frustum can be calculated using the formula:
V = (1/3)πh(r₁² + r₂² + r₁r₂),
where h is the height of the frustum, r₁ and r₂ are the radii of the larger and smaller bases, respectively.
In this case, we are given that the radii of the larger and smaller bases are 12 and 9 units, respectively. We also know that the two bases are 4 units apart, which means the height of the frustum is 4 units.
Substituting the given values into the formula, we have:
V = (1/3)π(4)(12² + 9² + 12*9)
= (1/3)π(4)(144 + 81 + 108)
= (1/3)π(4)(333)
= (4/3)π(333)
≈ 444π cubic units
Now, let's move on to calculating the total surface area of the frustum. The formula for the total surface area is:
A = π(r₁ + r₂)ℓ + πr₁² + πr₂²,
where ℓ is the slant height of the frustum.
Since the frustum is a right frustum, the slant height ℓ can be found using the Pythagorean theorem:
ℓ = √(h² + (r₁ - r₂)²)
Substituting the given values, we have:
ℓ = √(4² + (12 - 9)²)
= √(16 + 9)
= √25
= 5
Now we can calculate the total surface area:
A = π(12 + 9)(5) + π(12²) + π(9²)
= π(21)(5) + π(144) + π(81)
= 105π + 144π + 81π
= 330π square units
Finally, to find the product of the volume and total surface area, we multiply the two values:
VA = (444π)(330π)
≈ 146520π²
Therefore, the product of the volume and total surface area of the given right conical frustum is approximately 146520π².
Learn more about volume here:
https://brainly.com/question/21623450
#SPJ11
Two parallel lines are cut by a transversal.
If the measure of 24 is 100°, what is the measure of 27?
A. 90°
B. 80°
C. 180°
D. 100°

Answers
The value of the angle 7 is 80 degrees. Option B
What is a transversal line?A transversal line can be defined as a line that intersects two or more lines at distinct points.
It is important to note that corresponding angles are equal.
Also, the sum of angles on straight line is equal to 180 degrees.
From the information given, we have that;
Angle 3 and angle 7 are corresponding angles
Also, we have that
Angle 3 and angle 4 are on a straight line
equate the angles
<3 + 100 = 180
collect the like terms
<3 = 180 - 100
<3 = 80 degrees
Then, the value of <7 is 80 degrees
Learn about transversal lines at: https://brainly.com/question/24607467
#SPJ1
What is 5.8 to 1 decimal place?
Answers
At what points will the line y = x intersect the unit circle x2 y2 = 1? smaller value and larger value
Answers
\(The two equations given arey = x …. (1)x2 + y2 = 1 …. (2)Substitute equation (1) in (2)x2 + x2 = 12x2 = 1x2 = ½x = √1/2x = ±0.707As the square can be positive or negative we get x1 = 0.707 and x2 = -0.707From equation (1) we know that y = xy1= x1= 0.707y2= x2 = -0.707Therefore, the line y = x intersects the unit circle x2 + y2 = 1 at (0.707, 0.707) and (-0.707, -0.707).\)
What is intersect?A junction is a place where two lines come together or cross. In the illustration above, "point K is the intersection of line segments PQ and AB" is what we would state. The phrase "the line segment PQ crosses AB at position K" is another option.
Keep in mind that two line segments do not always need to intersect. In the illustration above, move point B higher until the intersection of the two line segments disappears. However, keep in mind that lines (as opposed to line segments) continue indefinitely in both directions, thus unless they are absolutely parallel, they will always cross someplace.
To know more about intersect, visit;
https://brainly.com/question/14217061
#SPJ4
simplify the expression
–4(5x)
Answers
Answer:
-20x
Step-by-step explanation:
the number outside of the parenthasis must be distributed to all numbers with in them.
ex:
-3(2x + 5) = -6x -15
Write an equation for a parabola that passes through the point (2,2) and has a vertex of (3,1)
Answers
The equation of the parabola will be;
y = (x - 3)² + 1
What is mean by Parabola?
A parabola is a set of points in the plane which are equidistant from the directrix and focus.
Given that;
The vertex of the parabola = (3 , 1)
A parabola passes through the point (2,2).
Now,
Since, The equation of parabola in vertex form is;
y = a (x - h)² + k
Where, (h , k) are vertex of the parabola.
So, The equation of parabola with vertex (3, 1) will be;
y = a (x - 3)² + 1
And, It passes through the point (2,2).
So we substitute the value of (2, 2) in place of (x, y) as;
2 = a (2 - 3)² + 1
2 = a + 1
a = 2 - 1
a = 1
Substitute the value of a in above equation, we get;
The equation of parabola as;
y = (x - 3)² + 1
Therefore, The equation of the parabola will be;
y = (x - 3)² + 1
Learn more about the parabola visit:
https://brainly.com/question/27703830
#SPJ1
The radius r of a sphere is increasing at the uniform rate of 0.3 inches per second. At the instant when the surface area S becomes 100pi square inches, what is the rate of increase, in cubic inches per second, in the volume V?
Answers
The rate of increase in the volume V is 30π cubic inches per second when the surface area S becomes 100π square inches.
What is volume?
Volume refers to the amount of three-dimensional space occupied by an object or a substance.
To find the rate of increase in the volume V of a sphere when the surface area S becomes 100π square inches, we need to use the formulas relating the surface area and volume of a sphere to its radius.
The surface area S of a sphere is given by the formula:
\(S = 4\pi r^2,\)
where r is the radius of the sphere.
The volume V of a sphere is given by the formula:
\(V = (4/3)\pi r^3.\)
To find the rate of increase in volume with respect to time, we need to differentiate the volume formula with respect to time.
Given that the radius r is increasing at a uniform rate of 0.3 inches per second, we can write:
dr/dt = 0.3 inches per second.
Now, let's differentiate the volume formula with respect to time:
\(dV/dt = d/dt [(4/3)\pi r^3].\)
Using the power rule of differentiation, we get:
\(dV/dt = (4/3)\pi * 3r^2 * (dr/dt).\)
Simplifying further, we have:
\(dV/dt = 4\pi r^2 * (dr/dt).\)
Since we want to find the rate of increase in cubic inches per second, we need to express the volume in cubic inches.
Substituting the value of the surface area S = 100π square inches into the surface area formula:
\(100\pi = 4\pi r^2.\)
Dividing both sides by 4π, we get:
\(r^2 = 25.\)
Taking the square root of both sides, we find:
r = 5.
Now, we can substitute the value of r into the rate of increase formula:
\(dV/dt = 4\pi(5^2) * (0.3).\)
Simplifying the expression:
dV/dt = 4π(25) * 0.3.
dV/dt = 30π cubic inches per second.
Therefore, the rate of increase in the volume V is 30π cubic inches per second when the surface area S becomes 100π square inches.
To learn more about volume visit:
https://brainly.com/question/463363
#SPJ4
Find the most general antiderivative of the function. (check your answer by differentiation. use c for the constant of the antiderivative. ) f(x) = x(18x 4)
Answers
Answer:
Below in bold.
Step-by-step explanation:
f(x) = x(18x + 4)
f(x) = 18x^2 + 4x
Antiderivative = 18 * (x^2+1)/(2 + 1) -+4x(1+1) / (1+1) + C
= 18x^3 / 3 + 4x^2 / 2 + C
= 6x^3 + 2x^2 + C.
Checking by differentiating:
f'(x) = 6*3 x^(3-1) + 2*2x^(2-1)
= 18x^2 + 4x
= x(18 -+4)
On a coordinate plane, a circle has a center at (4, 5) and a radius of 3 units.
Which equation represents a circle with the same center as the circle shown but with a radius of 2 units?
(x – 4)2 + (y – 5)2 = 2
(x – 4)2 + (y – 5)2 = 4
(x – 5)2 + (y – 4)2 = 2
(x – 5)2 + (y – 4)2 = 4
Answers
Answer:
(x - 4)² + (y - 5)² = 4
Step-by-step explanation:
The equation of a circle in standard form is
(x - h)² + (y - k)² = r²
where (h, k) are the coordinates of the centre and r is the radius
Here (h, k) = (4, 5) and r = 2, thus
(x - 4)² + (y - 5)² = 2², that is
(x - 4)² + (y - 5)² = 4 ← second option on list
The required equation represents a circle with the same center as the circle shown but with a radius of 2 units is (x-4)^2 + (y-5)^2 = 4
Equation of a circleThe standard equation of a circle is expressed as:
(x-a)^2 + (y-b)^2 = r^2
where:
(a, b) is the centre = (4, 5)
r is the radius = 3 units
Substitute to have;
(x-4)^2 + (y-5)^2 = 2^2
(x-4)^2 + (y-5)^2 = 4
Hence the required equation represents a circle with the same center as the circle shown but with a radius of 2 units is (x-4)^2 + (y-5)^2 = 4
Learn more on equation of circle here: https://brainly.com/question/14150470
Help please, I have been stuck on this answer for an hour. HELPP !

Answers
Answer:
(x+5)²=0
Step-by-step explanation:
I don't know how to explain this.. I'm sorry. It's an algebraic identity. If that helps..
Adi bought a bag for $25 and sold it at a loss of 10%. Find the selling price of the bag.
Answers
Answer:
The selling price of the bag is $22.5
Step-by-step explanation:
Buying Price = $25,
Selling Price = ?
Since they sold it at a loss of 10%,
So, they sold it for a price 10% less than the buying price,
or at 90% or 0.9 of the buying price,
so,
Selling Price = (0.9)(25) = $22.5