Parent function: y=x^(3) Shift 6.5 units to the left. Reflect across the y-axis. Shift upward 3.1 units.
Answers
The modified function, after applying the given transformations to the parent function y = x^3, is y = (-x + 6.5)^3 + 3.1.
To shift the parent function 6.5 units to the left, we replace x with (x + 6.5). This causes the function to be shifted horizontally to the left by 6.5 units. Next, to reflect the function across the y-axis, we negate the x term, resulting in (-x + 6.5). This reflection causes the function to be mirrored or flipped across the y-axis. Finally, to shift the function upward by 3.1 units, we add 3.1 to the entire function. This vertical shift moves the function vertically upward by 3.1 units. Combining all the transformations, we arrive at the modified function y = (-x + 6.5)^3 + 3.1.
In summary, the given transformations of shifting 6.5 units to the left, reflecting across the y-axis, and shifting upward by 3.1 units are applied to the parent function y = x^3. These transformations alter the shape, position, and orientation of the graph. The resulting modified function, y = (-x + 6.5)^3 + 3.1, represents the transformed graph of the original function.
Learn more about parent function here:
brainly.com/question/32030463
#SPJ11
Related Questions
Which points on the curve of x^2 - xy - y^2 = 5 have vertical tangent lines?
Answers
We need to differentiate this with respect to x to see if we can find an expression for the derivative of y at various points. That will be the slope of the tangent to the curve. Then we want to see where that derivative might be infinite -- i.e., where the tangent is vertical.
It's not written as a function, but it can still be differentiated using the chain rule:
x2 + xy + y2 = 3
(2x) + (x dy/dx + y dx/dx) + (2y dy/dx) = 0
(I used parentheses to show the differentiation of each term in the original equation.)
2x + x dy/dx + y + 2y dy/dx = 0
2x + y = -x dy/dx - 2y dy/dx
2x + y = dy/dx (-x -2y)
-(2x + y)/(x + 2y) = dy/dx
We have the derivative of y, but it's defined partly in terms of y itself. That's OK. Let's go on...
So where would the slope be infinite? That would happen when x + 2y = 0, or y = -x/2
Let's plug that in for y in the original equation to find points where that's the case.
x2 + xy + y2 = 3
x2 + x(-x/2) + (-x/2)2 = 3
x2 - x2/2 + x2/4 = 3
3x2 / 4 = 3
x2 = 4
x = ±2
So we have two x values where the tangent might be vertical. Let's plug them into the equation and see what the y values are. First x = 2...
x2 + xy + y2 = 3
4 + 2y + y2 = 3
y2 + 2y + 1 = 0
(y + 1)2 = 0
y = -1
So at the point (2, -1) the tangent is vertical.
Now try x = -2...
x2 + xy + y2 = 3
4 - 2y + y2 = 3
y2 - 2y + 1 =0
(y - 1)2 = 0
y = 1
So at the point (-2, 1) the tangent is vertical.
The measure of A is 100°. Angles A and B are supplementary. What is mB?
A. mB = 10°
B. mB = 80°
C. mB = 90°
D. mB = 180°
Answers
Answer:
The measure of angle B is 80°. B is the correct answer.
Answer:
B. mB = 80°
Step-by-step explanation:
Supplementary angles add to 180 degrees
100 +x = 180
x = 180-100
x = 80 degrees
the operation manager at a tire manufacturing company believes that the mean mileage of a tire is 20,138 miles, with a variance of 10,304,100. what is the probability that the sample mean would be less than 19,448 miles in a sample of 171 tires if the manager is correct? round your answer to four decimal places.
Answers
The probability that the sample mean would be less than 19,448 miles is 0.9972
Given,
The mean mileage of a tire, μ = 20,138
The standard deviation, σ = \(\sqrt{10,304,100}\) = 3210
Sample size, n = 171
We have to find the probability that the sample mean would be less than 19,448 miles.
That is,
P(X < 19448)
Since the sample size in this instance is greater than 30, we can utilise the central limit theorem and the z score formula provided by:
z = (X - μ) / (σ/√n)
The following would be the sample mean's distribution:
X ≈ N (μ, σ/√n)
In this situation, the z score was found to be:
z = (19448 - 20138) / (3210/√171)
z = -690 / 245.48
z = 2.81
Using the conventional table, we get the following:
P(z < 2.81) = 0.9972
That is,
The probability that the sample mean would be less than 19,448 miles is 0.9972
Learn more about probability here;
https://brainly.com/question/17011174
#SPJ4
i need help quick its due today please help show WORK and how to do it . NO links
a - 5 = -12
Answers
Answer:
a = -7
Step-by-step explanation:
a - 5 = -12
+5 +5
a = -7
Answer:
a = -7
Step-by-step explanation:
First, we have to make both sides equal. We do this by isolating the variable a. When we add 5 to -12, it becomes -7.
After heating up in a teapot, a cup of hot water is poured at a temperature of 203∘ F. The cup sits to cool in a room at a temperature of 69∘F. Newton's Law of Cooling explains that the temperature of the cup of water will decrease proportionally to the difference between the temperature of the water and the temperature of the room, as given by the formula below:
T=Ta+(T0-Ta)e^-kt
Ta = the temperature surrounding the object
T0 = the initial temperature of the object
t= the time in minutes
T= the temperature of the object after t minutes
k= decay constant
The cup of water reaches the temperature of 185∘F after 1.5 minutes. Using this information, find the value of k, to the nearest thousandth. Use the resulting equation to determine the Fahrenheit temperature of the cup of water, to the nearest degree, after 4.5 minutes.
Enter only the final temperature into the input box.
Answers
The Fahrenheit temperature of the cup of water, after 4.5 minutes, is given as follows:
155ºF.
How to obtain the temperature?The temperature function is defined as follows:
\(T(t) = T_a + (T_0 - T_a)e^{-kt}\)
Considering the surrounding and initial temperature, we have that the function is given as follows:
\(T(t) = 69 + 135e^{-kt}\)
The temperature after 1.5 minutes is of 185ºF, hence the coefficient k is obtained as follows:
\(185 = 69 + 135e^{-1.5k}\)
\(e^{-1.5k} = \frac{116}{135}\)
\(k = -\frac{\ln{\left(\frac{116}{135}\right)}}{1.5}\)
k = 0.1011.
Hence:
\(T(t) = 69 + 135e^{-0.1011t}\)
Hence the temperature after 4.5 minutes is given as follows:
\(T(4.5) = 69 + 135e^{-0.1011 \times 4.5}\)
T(4.5) = 155ºF.
More can be learned about Newton's Law of Cooling at https://brainly.com/question/10321943
#SPJ1
please help!
Q2: Solve the given Differential Equation by Undetermined Coefficient-Annihilator
Approach. y" +16y=xsin4x
Answers
The general solution is the sum of the complementary and particular solutions: y(x) = y_c(x) + y_p(x) = c1 cos(4x) + c2 sin(4x) + ((1/16)x + 1/8) sin(4x) + (Cx + D) cos(4x).
y" + 16y = x sin(4x) using the method of undetermined coefficients-annihilator approach, we follow these steps:
Step 1: Find the complementary solution:
The characteristic equation for the homogeneous equation is r^2 + 16 = 0.
Solving this quadratic equation, we get the roots as r = ±4i.
Therefore, the complementary solution is y_c(x) = c1 cos(4x) + c2 sin(4x), where c1 and c2 are arbitrary constants.
Step 2: Find the particular solution:
y_p(x) = (Ax + B) sin(4x) + (Cx + D) cos(4x),
where A, B, C, and D are constants to be determined.
Step 3: Differentiate y_p(x) twice
y_p''(x) = -32A sin(4x) + 16B sin(4x) - 32C cos(4x) - 16D cos(4x).
Substituting y_p''(x) and y_p(x) into the original equation, we get:
(-32A sin(4x) + 16B sin(4x) - 32C cos(4x) - 16D cos(4x)) + 16((Ax + B) sin(4x) + (Cx + D) cos(4x)) = x sin(4x).
Step 4: Collect like terms and equate coefficients of sin(4x) and cos(4x) separately:
For the coefficient of sin(4x), we have: -32A + 16B + 16Ax = 0.
For the coefficient of cos(4x), we have: -32C - 16D + 16Cx = x.
Equating the coefficients, we get:
-32A + 16B = 0, and
16Ax = x.
From the first equation, we find A = B/2.
Substituting this into the second equation, we get 8Bx = x, which gives B = 1/8.
A = 1/16.
Step 5: Substitute the determined values of A and B into y_p(x) to get the particular solution:
y_p(x) = ((1/16)x + 1/8) sin(4x) + (Cx + D) cos(4x).
Step 6: The general solution is the sum of the complementary and particular solutions:
y(x) = y_c(x) + y_p(x) = c1 cos(4x) + c2 sin(4x) + ((1/16)x + 1/8) sin(4x) + (Cx + D) cos(4x).
learn more about general solution
https://brainly.com/question/31491463
#SPJ11
Suppose the sample mean CO2CO2 level is 418 ppm.418 ppm. Is there any evidence to suggest that the population mean CO2CO2 level has increased
Answers
The probability that sample is greater than 418 will be is 6.533.
What is a probability?Probability is the occurence of likely events. It is the area of mathematics that deals with numerical estimates of the likelihood that an event will occur or that a statement is true.
Here we have
\(\mu=397.64,n=40,\sigma=20\)
According to central limit theorem, the sampling distribution of mean will be normal with mean
\(\mu_{\bar{x}}=\mu=397.64\)
and standard deviation
\(\sigma_{\bar{x}}=\frac{\sigma}{\sqrt{n}}=\frac{20}{\sqrt{40}}=3.1623\)
The z-score for\(\bar{x}=418\) is
\(z=\frac{\bar{x}-\mu_{\bar{x}}}{\sigma_{\bar{x}}}=\frac{418-397.34}{3.1623}=6.533\)
Therefore, the probability that sample is greater than 418 will be
\(P(\bar{x} > 418)=P(z > 6.533)\)
Learn more about probability here:
https://brainly.com/question/29557037
#SPJ4
Incomplete Question
Carbon dioxide (CO2) is one of the primary gases contributing to the greenhouse effect and global warming. The mean amount of CO2 in the atmosphere for March 2013 was 397.34 parts per million (ppm). Suppose 40 atmospheric samples are selected at random in May 2013 and the standard deviation for CO2 in the atmosphere is σ = 20 ppm. (1 pt.)
c) Suppose the sample mean CO2 level is 400. Is there any evidence to suggest that the population mean CO2 level has increased?
In Exercises 1-3, graph AABC and its image after a reflection in the given line.
1. A(0, 2), B(1, -3), C(2, 4); x-axis
1.
2. A(-2,-4), B(6,2), C(3. – 5); y-axis
3. A(4, -1), B(3, 8), C(-1, 1); y = -2
Answers
The figures after each reflection are given at the end of the answer.
Reflection over the x-axis
The rule for the reflection over the x-axis is:
(x,y) -> (x, -y)
Hence the signal of the y-coordinate is changed.
Then the coordinates of the image of triangle ABC are given as follows:
A'(0,-2), B'(1,3) and C(2,-4)
Reflection over the y-axis
The rule for the reflection over the x-axis is:
(x,y) -> (-x, y)
Hence the signal of the x-coordinate is changed.
Then the coordinates of the image of triangle ABC are given as follows:
A'(2,-4), B'(-6,2) and C'(-3,-5)
Reflection over y = -2The rule for the reflection over the line y = -2 is:
(x,y) -> (x, y +/- constant)
The constants for each point are given as follows:
A': -3, hence point (4,-3), as -1 is one unit above y = -2, hence the reflected coordinate will be one unit below.B': -12, hence point (3,-12), as 8 is 10 units above y = -2, hence the reflected coordinate will be ten units below.C': -5, hence point (-1, -5), as 1 is 3 units above y = -2, hence the reflected coordinate will be three units below at y = -5.More can be learned about reflections at https://brainly.com/question/27224272
#SPJ1



4х + 1= 3x + 2
does it have no solution one solution or infinitely many solutions
Answers
Step-by-step explanation:
4x-3x=2-1
×=1
that's fine
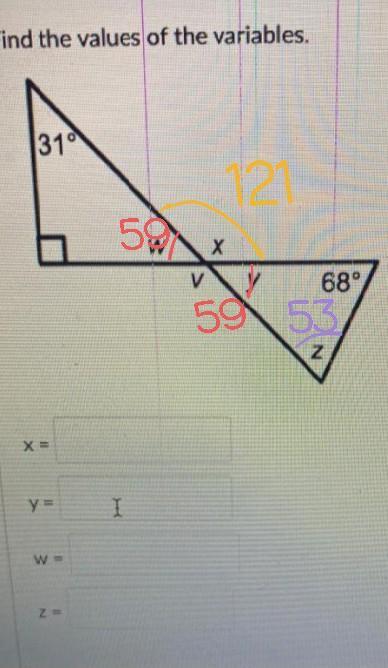
Find the values of the variables.
31
W
Х
V
у
68°
Z

Answers
Answer:
X=121, y=59, w=59, z=53
Step-by-step explanation:
To find w, we know that the interior angles of a triangle are 180°. Thus ↓
180-31-90=59
For y, we know that y and w are opposite angles. Therefore, y = w = 59.
To find x, we know that there is a one straight line, so therefore we use ↓
180-59=121
Lastly, to find z, we know that the interior angles of a triangle are 180°. Thus ↓
180-59-68=53
I've attached a photo for better understanding. Hope this helps =)
Can somebody check my work? For geometry

Answers
Answer:
Yeah I think you're correct I got the same
Step-by-step explanation:
The Key Club has a goal to raise $1,700, which they need for new equipment, by conducting various fundraisers. First, they did a baked of their goal 2/5amount. Next, they did a goods sale and earned 3/8 BINGO night and earned of their goal amount. How much more money does the Key Club still need to earn in order to reach their goal?
Answers
The amount of money more that Key Club still need to earn in order to have reached their target is $ 382. 50
How to find the money needed ?To find the amount of money needed by Kay Club to get to their target, first, find the amount of money earned from the bake sale :
= 2 / 5 x Target amount
= 2 / 5 x 1, 700
= $ 680
Then, they did a good sale and earned 3 / 8 of the amount :
= 3 / 8 x 1, 700
= $ 637. 50
The amount of money that Key Club still needs is:
= Total amount - amount raised
= 1, 700 - 680 - 637. 50
= $ 382. 50
In conclusion. Key Club would still need to engage in other activities to be able to reach their goal of $ 1, 700 as they have to raise $ 382. 50.
Find out more on fundraisers at https://brainly.com/question/11052612
#SPJ1
40 points Please help!!!
What is the volume of this regular prism?
48.55 cubic inches
55.8 cubic inches
9.7 cubic inches
24.28 cubic inches

Answers
Answer:
V = 24.28 in ^3
Step-by-step explanation:
The area of the base is
A =5/2 × s × a where s is the side length and a is the apothem
A = 5/2 ( 2.13) * .87
A = 4.63275
The volume is
V = Bh where B is the area of the base and h is the height
V = 4.63275 ( 5.24)
V =24.27561 in^3
Rounding to the hundredth
V = 24.28 in ^3
Tell Me Which property the statement represents, algebraic like commuative or distributive thanks
1.8+9=q+18
5+(6+b)=(5+6)+b
2+y +4 = y+2+4
Answers
The system of equations that has a solution of approximately (1.8, –0.9) are: x+2y=0 and 6x-5y=15
What is equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign. In its simplest form in algebra, the definition of an equation is a mathematical statement that shows that two mathematical expressions are equal. For instance, 3x + 5 = 14 is an equation, in which 3x + 5 and 14 are two expressions separated by an 'equal' sign.
Here, we have,
we are given the following equations:
i) x-2y= 4
ii) 4x+5y= 8
iii) 6x-5y=15
iv) x+2y=0
Required:
Which system of equations has a solution of approximately (1.8, –0.9).
To find the approximate equations, substitute x and y for 1.8 and -0.9 into all the equations respectively and check the resulting values
i) Substitute (1.8, -0.9) in x-2y= 4:
1.8 - 2(-0.9) = 4.
1.8 + 1.8 = 4.
3.6 ≠ 4.
ii) Substitute (1.8, -0.9) in 4x+5y= 8
4(1.8) + 5(-0.9) = 8
7.2 - 4.5 = 8.
2.7 ≠ 8.
iii) Substitute (1.8, -0.9) in 6x-5y=15
6(1.8) - 5(-0.9) = 15.
10.8 + 4.5 = 15
15.3 ≠ 15.
This equation has a solution that is close, therefore it is correct.
iv) Substitute (1.8, -0.9) in x+2y=0
1.8 + 2(-0.9) = 0.
1.8 - 1.8 = 0.
0 = 0.
x + 2 y = 0 has the exact value, therefore it is also correct.
The system of equations that has a solution of approximately (1.8, –0.9) are: x+2y=0 and 6x-5y=15
To learn more on equation click:
brainly.com/question/24169758
#SPJ1
A store manager kept track of the number of newspapers sold each week over a seven-week period. The results are shown below. \( 87,87,215,154,288,235,231 \) Find the median number of newspapers sold.
Answers
The median number of newspapers sold over seven weeks is 223.
The median is the middle score for a data set arranged in order of magnitude. The median is less affected by outliers and skewed data.
The formula for the median is as follows:
Find the median number of newspapers sold. (87, 87, 215, 154, 288, 235, 231)
We'll first arrange the data in ascending order.87, 87, 154, 215, 231, 235, 288
The median is the middle term or the average of the middle two terms. The middle two terms are 215 and 231.
Median = (215 + 231)/2
= 446/2
= 223
In statistics, the median measures the central tendency of a set of data. The median of a set of data is the middle score of that set. The value separates the upper 50% from the lower 50%.
Hence, the median number of newspapers sold over seven weeks is 223.
To know more about the median, visit:
brainly.com/question/300591
#SPJ11
Which value must be added to the expression x2 + x to make it a perfect-square trinomial? One-fourth One-half 1 4
Answers
Answer:
a. ¼
(Below is the Screenshot on EdgeCourseware)

1/4 must be added to the given expression to make it a perfect-square trinomial.
The given expression is x²+x.
What is an expression?An expression is a combination of terms that are combined by using mathematical operations such as subtraction, addition, multiplication, and division.
Add 1/4 to the given expression, we get
x²+x+1/4
= x²+x+(1/2)²
= (x+1/2)²
Verification:
x²+2.x.1/2+1/4
= x²+x+1/4
Therefore, 1/4 must be added to the given expression to make it a perfect-square trinomial.
To learn more about an expression visit:
https://brainly.com/question/14083225.
#SPJ2
the test in an if function must evaluate to either a true or a false.
Answers
Yes, the test in an "if" function must evaluate to either a True or a False value.
An "if" function, also known as a conditional statement, is used to perform specific actions based on whether a certain condition is met or not. The test or condition within the "if" function needs to be evaluated as either True or False in order for the program to decide which action to execute. If the test evaluates to True, the program will perform the action within the "if" block, and if it evaluates to False, it will either execute the action in the "else" block (if present) or simply skip the "if" block.
When using an "if" function in programming, it is essential for the test or condition within the statement to result in a boolean value, which is either True or False. This is because the program needs to determine whether the condition is met or not, so it can decide which set of actions to execute. If the condition evaluates to True, the code within the "if" block will be executed, while if it evaluates to False, the code within the "else" block (if present) will be executed, or the "if" block will be skipped altogether.
To know more about function visit:-
https://brainly.com/question/30721594
#SPJ11
When Brandon was told that he correctly answered 80% of the items on a math achievement test, he asked how his performance compared with that of the average test taker. Brandon's concern was directly related to the issue of
Answers
Brandon's concern about his performance compared to the average test taker, even after he correctly answered 80% of the items on a math achievement test.
How well an individual has performed in a certain area or task is assessed by two basic types of testing: criterion-referenced and norm-referenced tests. The primary goal of the criterion-referenced test is to identify how well the person being tested can perform certain tasks. In contrast, norm-referenced tests compare the results of a person's test to a norm or average score.
This enables the results to be compared to a large sample of test-takers and allows for comparisons between the performance of different people .The issue of norm-referenced test is related to Brandon's concern because the 80% score he achieved on the math achievement test will only tell him how well he performed on that particular test, but not how well he performed when compared to the average test-taker.
To know more about Brandon's visit:
https://brainly.com/question/2283795
#SPJ11
Let f(x) = Find: 3x - 1 8x1 1) Domain (in interval notation) 2) y-intercept(s) at the point(s) 3) x-intercept(s) at the point(s) 4) x-value of any holes 5) Equation of Vertical asymptotes 6) Equation of Horizontal asymptote Write intercepts as ordered pairs. Write asymptotes as equations. Write DNE if there is no solution.
Answers
The intercepts, asymptotes, and domain of the given function are as follows:
Domain: (-∞,-1/8) ∪ (-1/8,∞)
y-intercept: (0, -1/8)
x-intercept: (1/3, 0)
Vertical asymptote: x = -1/8
Horizontal asymptote: y = 3/8.
The given function is: f(x) = (3x - 1) / (8x + 1)
To simplify the function, we can rewrite it as:
f(x) = [3(x - 1/3)] / [8(x + 1/8)] = (3/8) * [(x - 1/3)/(x + 1/8)]
Domain:
The function is defined for all x except when the denominator is zero, i.e., (8x + 1) = 0
This occurs when x = -1/8
Therefore, the domain of the function is: D = (-∞,-1/8) U (-1/8,∞)
In interval notation: D = (-∞,-1/8) ∪ (-1/8,∞)
y-intercept(s):
When x = 0, we get: f(0) = (-1/8)
Therefore, the y-intercept is (0, -1/8)
x-intercept(s):
When y = 0, we get: 3x - 1 = 0 => x = 1/3
Therefore, the x-intercept is (1/3, 0)
x-value of any holes:
There are no common factors in the numerator and denominator; therefore, there is no hole in the graph.
Equation of Vertical asymptotes:
Since the denominator of the simplified function is zero at x = -1/8, there is a vertical asymptote at x = -1/8.
Equation of Horizontal asymptote:
When x approaches infinity (x → ∞), the terms with the highest degree become more significant. The degree of the numerator and denominator is the same, i.e., 1. Therefore, we can apply the rule for finding the horizontal asymptote:
y = [Coefficient of the highest degree term in the numerator] / [Coefficient of the highest degree term in the denominator]
y = 3/8
Therefore, the equation of the horizontal asymptote is y = 3/8.
To know more about asymptotes
https://brainly.com/question/32038756
#SPJ11
T/F. he triple exponential smoothing method uses seasonality variations in the analysis of the data.
Answers
False. The triple exponential smoothing method does consider seasonality variations in the analysis of the data, along with trend and level components, to provide accurate forecasts.
The statement is false. Triple exponential smoothing, also known as Holt-Winters method, is a time series forecasting method that incorporates trend and seasonality variations in the analysis of the data, but it does not specifically use seasonality variations.
Triple exponential smoothing extends simple exponential smoothing and double exponential smoothing by introducing an additional component for seasonality. It is commonly used to forecast data that exhibits trend and seasonality patterns. The method takes into account the level, trend, and seasonality of the time series to make predictions.
The triple exponential smoothing method utilizes three smoothing equations to update the level, trend, and seasonality components of the time series. The level component represents the overall average value of the series, the trend component captures the systematic increase or decrease over time, and the seasonality component accounts for the repetitive patterns observed within each season.
By incorporating these three components, triple exponential smoothing can capture both the trend and seasonality variations in the data, making it suitable for forecasting time series that exhibit both long-term trends and repetitive seasonal patterns.
Learn more about variations at: brainly.com/question/17287798
#SPJ11
What is the slope of the line on the graph?
Enter your answer in the box.

Answers
Answer:
m = -2
Step-by-step explanation:
because of rise/run you can simply see the slope
set y=0 and apply the zero product property\(y = x {}^{2} + 2x - 3\)
Answers
Given:
\(y=x^2+2x-3\)\(\begin{gathered} 0=x^2+2x-3 \\ 0=x^2-x+3x-3 \\ 0=x(x-1)+3(x-1) \\ 0=(x-1)(x+3) \end{gathered}\)\(x=1,-3\)Karl is making a pot of chili. The recipe calls for StartFraction 3 Over 8 EndFraction cup of chili powder, but Karl only wants to use half as much so it won’t be so spicy. How much chili powder should Karl use?
StartFraction 1 Over 16 EndFraction of a cup
StartFraction 1 Over 8 EndFraction of a cup
StartFraction 3 Over 16 EndFraction of a cup
Three-fourths of a cup
Answers
Answer:Karl is making a pot of chili. The recipe calls for StartFraction 3 Over 8 EndFraction cup of chili powder, but Karl only wants to use half as much so it won’t be so spicy. How much chili powder should Karl use?
StartFraction 1 Over 16 EndFraction of a cup
StartFraction 1 Over 8 EndFraction of a cup
StartFraction 3 Over 16 EndFraction of a cup
Three-fourths of a cup
Step-by-step explanation:
Karl is making a pot of chili. The recipe calls for StartFraction 3 Over 8 EndFraction cup of chili powder, but Karl only wants to use half as much so it won’t be so spicy. How much chili powder should Karl use?
StartFraction 1 Over 16 EndFraction of a cup
StartFraction 1 Over 8 EndFraction of a cup
StartFraction 3 Over 16 EndFraction of a cup
Three-fourths of a cup
Answer:
3/4 or D
Step-by-step explanation:
can someone please help

Answers
The coordinates of K such that JK is 2/9 of JL are given as follows:
K(3, -4).
How to obtain the coordinates of K?The coordinates of K are obtained applying the proportions in the context of the problem.
Considering that JK is 2/9 of JL, the equation is given as follows:
K - J = 2/9(L - J).
Hence the x-coordinate of K is obtained as follows:
x + 3 = 2/9(24 + 3)
x + 3 = 6
x = 3.
The y-coordinate of K is obtained as follows:
y - 4 = 2/9(-32 - 6)
y - 4 = -8
y = -4.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
a company's revenue from selling x units of an item is given as dollars. if sales are increasing at the rate of 70 per day, find how rapidly revenue is growing (in dollars per day) when 420 units have been sold.
Answers
The rate of growth of revenue when 420 units have been sold is R'(420) = R'(350)..
Revenue from selling x units = R(x). Also, sales are increasing at a rate of 70 per day. That means if x units are sold today, then tomorrow, the units sold would be (x + 70) units. Rate of increasing sales = 70 per day. Now, when 420 units have been sold:
Initial units sold = x = 420 - 70 = 350 units
Total units sold = 420 units
Number of units sold today = 420 - 350 = 70 units
Now, Revenue generated from 350 units of the item = R(350)
Revenue generated from 420 units of the item = R(420)
Rate of growth of revenue when 420 units have been sold = R'(420)\
From the definition of the derivative:
R'(x) = lim_ {h→0} {R(x+h) - R(x)}/{h}
R'(420) = lim_ {h→0} {R(420+h) - R(420)}/{h}
R(420) = R(350 + 70) = R(350) + R'(350) * (70)And, R(420 + h)
= R(350 + 70 + h) = R(350) + R'(350) * (70 + h), Using these equations,
R'(420) = lim_ {h→0} {R(350) + R'(350) * (70 + h) - R(350) - R'(350) * (70)}/{h}
= lim_ {h→0} {R'(350) * h}/{h}
= R'(350)
Thus, the rate of growth of revenue when 420 units have been sold is R'(420) = R'(350).
To learn more about rate of growth refer :
https://brainly.com/question/14263843
#SPJ11
!!!!NEED HELP ASAP!!!! NO LINKS OR REPORT

Answers
Answer:
Step-by-step explanation:
Infinitely many solutions means that one side of the equals sign is exactly the same as the other side. We can achieve that easily by multiplying through the parenthesis and then combining like terms.
2(6x + 4) - 5x is 12x + 8 - 5x which simplifies down to 7x + 8. That is what goes on the right side of your equation.
Which is reflex angle
a.180° b.280° c.270°
Answers
Answer:
b)280° and c) 270°
A reflex angle is an angle which is more than 180° but less than 360°
If my answer helped, kindly mark me as the brainliest!!
Thank You!!
Step-by-step explanation:
180 is reflex angle.
hope it's helpful
Steam and leaf plot question

Answers
Answer:
10 i think
Step-by-step explanation:
since the number on the left side of the lin represents 10s and the right side represents ones, so there are 10 units in between 15 and 30 (sorry for the bad explanation lol)
helppppppppppppppppppppppp

Answers
Answer:
100
Step-by-step explanation:
let 's' = score on 6th test
[88(5) + s] ÷ 6 = 90
\(\frac{(440+s)}{6}\) = 90
cross-multiply to get:
440 + s = 540
s = 100
12. Extend Your Thinking Would you draw
a fraction model or use a number line to
represent the number 323? Explain your
choice.
Answers
a Fraction
_________
3 2/3
Fraction number is 3 × 3 + 2 = 9+2=11