Patrickhas$600inasavingsaccountthatearns10%interestperyear.Theinterestisnotcompounded.Howmuchwillhehaveintotalin1year?
Answers
Therefore, Patrick will have a total of $660 after one year.
What is percent?Percent is a way of expressing a number as a fraction of 100. It is denoted by the symbol "%". Percentages are used to represent proportions, rates, and percentages of a total. For example, if you say "20%", it means 20 out of 100, or 20/100. So, percentages are a useful tool for expressing a fraction or a proportion in a more easily understandable format.
Here,
If the interest is not compounded, it means that Patrick will earn a simple interest of 10% of his initial amount after one year.
So the interest earned after one year is:
10% of $600 = 0.10 x $600 = $60
Therefore, Patrick will have a total of:
$600 (initial amount) + $60 (interest earned) = $660 after one year.
To know more about percent,
https://brainly.com/question/29172752
#SPJ1
Complete question:
Patrick has $600 in a savings account that earns 10% interest per year. The interest is not compounded. How much will he have in total in 1 year?
Related Questions
Look at the following numbers: -10, -5, 0, 5 Which pair of numbers has a sum of 0? (5 points) a -10, 5 b 0, 5 c 5, -5 d -5, 0
Answers
Answer:
c) 5, -5
Step-by-step explanation:
5 + (-5)
= 5 - 5
= 0
Find the area and the circumference of a circle with a radius of 2km. Write your answers in terms of pi, and be sure to include the correct units in your answers.
Answers
The area and the circumference of the circle would be 4π square kilometers and 4π kilometers respectively.
Area and circumference of a circleThe area of a circle with a radius r is given by:
A = πr^2The circumference of a circle with a radius r is given by:
C = 2πr.Given that the radius of the circle is 2km, we can substitute r = 2 into these formulas to find the area and circumference:
Area = πr^2 = π(2km)^2 = 4π km^2Circumference = 2πr = 2π(2km) = 4π kmIn other words, the area and the circumference of the circle are 4π square kilometers and 4π kilometers respectively.
More on circles can be found here: https://brainly.com/question/29142813
#SPJ1
Represent the following expressions as a power of the number a (a≠0)((a^2)^−2)^5÷(a^4a)^3
Answers
The answer will be \(a^{-20-12a}\) that can be find out using exponential function.
What are exponential function ?
Exponential functions model a relationship in which a constant change in the independent variable gives the same proportional change.
Like, f(x) = \(x^{a}\)
x is base and a is power.
Basic rules to solve this function :
1. If we take the product of two exponentials with the same base, we simply add the exponents:
x^ a * x^ b = x^ a + b.
2. If we take the quotient of two exponentials with the same base, we simply subtract the exponents:
x^ a / x^ b = x^ a-b
3. We can raise exponential to another power, or take a power of a power. The result is a single exponential where the power is the product of the original exponents:
x^ (a)^ b = x^ (ab).
In given equation, \({a^{2^{-2^5}}/{a^{4a^3}}\)
So the answer is a^(-20-12a).
Learn more about exponential function using given link :
https://brainly.com/question/2456547
#SPJ1
Whata 7,500lb= to tons what's it

Answers
Answer:
3.75 tons djdhdjrjrhejejjwjwjsjs
Answer:
3.75 US tons
Step-by-step explanation:
1 ton =2000 pounds
so 7,500÷2000 =3.75
What term has the y, in the equation 3y + 4 = x
Answers
-12 will be the term for y
Let us suppose that x= 0
then we will get
3y + 4 = x
and then it will be
3y+ 4 = 0
Now, we will move 4 to the right hand side and it being positive this side will become negative on right hand side
3y= -4
now,
3y = 1/4
y = 1/[4*3]
y=1/12
y= - 12
Hence the answer will be y= -12
To learn more about equation -
https://brainly.com/question/24262709
Erika sells bicycles at a store. She is paid a monthly salary plus a bonus on each bike she sells. Her monthly pay is modeled in the table. Choose the linear equation below that best represents this data.
Answers
Answer: Show the table
Step-by-step explanation:
SHow the table
What is 1-1/2? Savas Realize math problem
Answers
\( \frac{1 - 1}{2} = \frac{0}{2} \)
the result is 0
2x² + 10 factorización
Answers
Answer:
2(x² + 5)
Step-by-step explanation:
To factor 2x² + 10, we can first factor out the greatest common factor of the terms, which is 2:
2x² + 10 = 2(x² + 5)
We can't factor anymore, so the answer is:
2(x² + 5)
Answer:
2(x² + 5)
Step-by-step explanation:
To factorise this, do the distributive property backwards. In other words:
2x² + 10
2x² ÷ 2 + 10 ÷ 2
x² + 5
2(x² + 5)
∴ 2(x² + 5) is the answer
Morre Math HARDDDDDDDD

Answers
Answer:
the person above is right it's 4.5 units
give them the crown
Write the equation of a line with a slope of 1 and a y-intercept of 3. Do not use spaces in your response. *
Answers
Answer:
Y=X+3
Step-by-step explanation:
Please answer this It would mean alot to me.

Answers
The expression 8x + 4y is not equivalent to 4(2x + 1). Therefore, 8x + 4y = 4(2x + y)
How to find equivalent expression?Two expressions are said to be equivalent if they have the same value irrespective of the value of the variable(s) in them.
Equivalent expressions are expressions that have similar value or worth but do not look the same.
Let's determine whether the expression 8x + 4y is equivalent to 4(2x + 1).
Let's factorise to know whether the expressions are equivalent.
Therefore, using the common factors,
8x + 4y = 4(2x + y)
Hence, the expression are not equivalent .
learn more on equivalent expression here: https://brainly.com/question/28170201
#SPJ1
One positive number is 9 more than twice another. If their product is 95, find the numbers.
Answers
Answer:
The numbers are 19 and 5
Step-by-step explanation:
Given
Let the numbers be \(x\ and\ y.\)
So:
\(x = 9 + 2y\) --- First statement
\(x*y = 95\) --- second statement
Required
Find x and y
Substitute \(x = 9 + 2y\) in \(x*y = 95\)
\((9 + 2y) * y = 95\)
\(9y + 2y^2 = 95\)
Rewrite as:
\(2y^2 + 9y - 95 = 0\)
Expand
\(2y^2 -10y +19y- 95 = 0\)
Factorize
\(2y(y -5) +19(y- 5) = 0\)
\((2y +19)(y- 5) = 0\)
Solve for y
\(2y + 19 =0\) or \(y - 5 = 0\)
\(2y = -19\) or \(y = 5\)
\(y = -\frac{19}{2}\) or \(y=5\)
Since the numbers are positive, we take only:
\(y=5\)
Substitute \(y=5\) in \(x = 9 + 2y\)
\(x = 9 + 2 * 5\)
\(x = 9 + 10\)
\(x = 19\)
The numbers are 19 and 5
Fill in the missing values below one at a time to find the quotient when x^3 - x^2 - 3x + 2 is divided by x - 2.

Answers
Therefore, the quotient when x³ - x² - 3x + 2 is divided by x - 2 is x² - 2x - 5 with a remainder of -3.
To find the quotient when x³ - x² - 3x + 2 is divided by x - 2, we will use the long division method. Here is the solution:
Step 1: The first term of the quotient is x². Multiply x² by x - 2 to get x³ - 2x². Subtract this product from x³ - x² to get: x² - 3x² = -2x²
Step 2: Bring down the next term of the dividend, which is -3x. The new dividend is -2x² - 3x.
Step 3: The second term of the quotient is -2x. Multiply -2x by x - 2 to get -2x² + 4x. Subtract this product from -2x² - 3x to get -5x.
Step 4: Bring down the last term of the dividend, which is +2. The new dividend is -5x + 2. Step 5: The third term of the quotient is -5. Multiply -5 by x - 2 to get -5x + 10. Subtract this product from -5x + 2 to get -3.
For such more question on Multiply
https://brainly.com/question/29793687
#SPJ8
let's see who can solve this. pleseeee

Answers
The correlation coefficient between X and Y is Corr(X, Y) = 0.
To calculate the marginal distribution of X and Y, we need to integrate the joint probability density function (PDF) over the appropriate ranges.
a. Marginal distribution of X:
To find the marginal distribution of X, we integrate the joint PDF over the range of Y:
∫[0, 1] J(x, y) dy
Since the joint PDF is defined as J(x, y) = 1 for 0 ≤ y ≤ x ≤ 1 and J(x, y) = 0 otherwise, the integral becomes:
∫[0, x] 1 dy = x, for 0 ≤ x ≤ 1
So, the marginal distribution of X is simply X(x) = x for 0 ≤ x ≤ 1.
b. Expectation of X:
The expectation (mean) of X can be calculated as the integral of x times the marginal PDF of X:
\(E(X) = ∫[0, 1] x * X(x) dx = ∫[0, 1] x^2 dx = [x^3/3] from 0 to 1 = 1/3\)
Therefore, the expectation of X is E(X) = 1/3.
c. Variance of X:
The variance of X can be calculated using the formula:
\(Var(X) = E(X^2) - (E(X))^2E(X^2) = ∫[0, 1] x^2 * X(x) dx = ∫[0, 1] x^3 dx = [x^4/4] from 0 to 1 = 1/4Var(X) = 1/4 - (1/3)^2 = 1/4 - 1/9 = 5/36\)
Therefore, the variance of X is Var(X) = 5/36.
d. Covariance of X and Y:
The covariance of X and Y can be calculated as:
Cov(X, Y) = E(XY) - E(X)E(Y)
Since the joint PDF J(x, y) = 1 for 0 ≤ y ≤ x ≤ 1, the integral becomes:
\(E(XY) = ∫[0, 1] ∫[0, x] xy dy dx = ∫[0, 1] [(x^2)/2] dx = [(x^3)/6] from 0 to 1 = 1/6\)
\(E(X) = 1/3 (from part b)E(Y) = ∫[0, 1] ∫[0, x] y J(x, y) dy dx = ∫[0, 1] [(x^2)/2] dx = [(x^3)/6] from 0 to 1 = 1/6\)
Cov(X, Y) = 1/6 - (1/3)(1/6) = 0
Therefore, the covariance of X and Y is Cov(X, Y) = 0.
e. Correlation coefficient between X and Y:
The correlation coefficient can be calculated using the formula:
Corr(X, Y) = Cov(X, Y) / √(Var(X) * Var(Y))
Since the covariance of X and Y is 0, the correlation coefficient will also be 0.
Therefore, the correlation coefficient between X and Y is Corr(X, Y) = 0.
f. Conclusion based on the correlation coefficient:
The correlation coefficient of 0 indicates that there is no linear relationship between X and Y. In this case, the fraction of male runners (X) and the
for more such question on correlation visit
https://brainly.com/question/13879362
#SPJ8
From least to greatest, What are the x–coordinates of the three points where the graphs of the equations intersect? If approximate, enter values to the hundredths.
,
,
Answers
The x-coordinates where the graphs of the equations intersect are x = -1 and x = 3
How to determine the x-coordinates where the graphs of the equations intersect?From the question, we have the following parameters that can be used in our computation:
y = 2x
y = x² - 3
The x-coordinates where the graphs of the equations intersect is when both equations are equal
So, we have
x² - 3 = 2x
Rewrite the equation as
x² - 2x - 3 = 0
When the equation is factored, we have
(x + 1)(x - 3) = 0
So, we have
x = -1 and x = 3
Hence, the x-coordinates are x = -1 and x = 3
Read more about equations at
https://brainly.com/question/148035
#SPJ1
Question
From least to greatest, What are the x–coordinates of the three points where the graphs of the equations intersect? If approximate, enter values to the hundredths.
y = 2x
y = x² - 3
Simplify your answer as much as possible.

Answers
By using the substitution method, we will see that the value of y is 23.
How to solve the system of equations?Here we have a system of linear equations, the system is:
y - x = 11
x = 12
The second equation is trivial, it just gives the value of x. Then we can use the substitution method and replace it in the first equation, then we will get:
y - 12 = 11
Now we can solve this for y, we will get:
y = 11 + 12
y = 23
That is the value of y.
LEarn moer about systems of equations at:
https://brainly.com/question/13729904
#SPJ1
Plot the points A(9, 11) and B(–3, –5). Find midpoint M of AB. Then show that AM = MB and AM + MB =AB
Answers
Answer:
The midpoint is (3, 3).
Step-by-step explanation:
We are given the two points A(9, 11) and B(-3, -5).
The midpoint is given by:
\(\displaystyle M=\Big(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\Big)\)
So:
\(\displaystyle M = \Big( \frac{9+(-3) }{2}, \frac{ 11+(-5) }{2} \Big) = (3,3)\)
The midpoint is (3, 3).
We want to show that AM = MB.
We can use the distance formula:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2\)
The distance between A(9, 11) and M(3, 3) will then be:
\(AM=\sqrt{(9-3)^2+(11-3)^2}=\sqrt{6^2+8^2}=\sqrt{100}=10\)
And the distance between B(-3, -5) and M(3, 3) will be:
\(MB = \sqrt{ (3-(-3))^2 + (3-(-5))^2 } = \sqrt{(6)^2+(8)^2} = \sqrt{ 100 } = 10\)
So, AM = MB = 10.
Since AM = MB = 10, AM + MB = 10 + 10 = 20.
So, we want to prove that AB = 20.
By the distance formula:
\(AB=\sqrt{(9-(-3))^2+(11-(-5))^2}=\sqrt{12^2+16^2}}=\sqrt{400}=20\stackrel{\checkmark}{=}20\)
If 51x + 23y = 116 and 23x + 51y = 106, then find the value of (x – y).
Answers
Step-by-step explanation:
51x + 23y = 116 ……….. (i)
23x + 51y = 106 ………… (ii)
Subtracting (ii) from (i)
28x – 28y = 10
28(x – y) = 10
⇒ (x – y) = 10/28 = 5/14
The solution of the expression x- y is 5/14.
Given Equation:
Equation 1: 51x + 23y = 116
Equation 2: 23x + 51y = 106
Now, multiply 23 in equation 1 and 51 in equation 2 gives
Equation 3: 1173x + 529y = 2,668
Equation 4: 1173x + 2601 y = 5406
Solving the Equation 1 and (3) gives
2601y - 529y = 5406 - 2668
2072y= 2738
y = 37/28.
Substituting the value of y= 37/28 in Equation 1 gives
51x + 23(37/28)= 116
51 x= 2397/28
x= 47/28
So, the value of x-y
= 47/28 - 37/28
= 10/28
= 5/14
Learn more about Equation here:
https://brainly.com/question/29657983
#SPJ4
Three dogs eat 30 pounds of food in 10 days. If each dog eats the same amount, how much food does 1 dog eat in 1 day? 1 pound 3 pounds 9 pounds 10 pounds

Answers
Answer:
Unable to read entire question, but see explanation for answer
Step-by-step explanation:
First, you need to find the unit rate per dog. If it takes 3 dogs 10 days to finish 30 pounds of food, then it takes 1 dog 1 day to finish 1 pound of food. I cannot read the entirety of the question because of the cropping, but you can find how much food a single dog eats in that amount of days by just multiplying by the number of days (say, 1 pound in 1 day, or 3 pounds in 3 days). Hope this helps!
Answer:
1
Step-by-step explanation:
took test
Solve for y.
3(y-2) = y +4-2(-5y-2)
Simplify your answer as much as possible.
Answers
Answer:
y = -7/4
Step-by-step explanation:

The graph below is the function f(x)

Answers
The required answers are:
lim f(x) = -1
1-2-
lim f(x) = -1
1+2+
lim f(x) = -3
r2
f(2) = -3
How to solve thisGiven image has a graph of the function f(x)
To find \(\lim_{x\rightarrow 2^-}f(x), lim f(2) 12+, lim f(x) 12 and f(2)\)
We have from the image of the graph the function f(x) is a discontinuous function with x=2 is the point of discontinuity.
Now from the graph the value of f(x) at x=2 i.e. f(2) = -3 as the graph has a bold dot at y=-3.
Next \(\lim_{x\rightarrow 2^-}f(x)=\lim_{x\rightarrow 2^+}f(x)=-1\) as in the graph of f(x) it has a small circle at y = -1.
As f(2) = -3 so \(\lim_{x\rightarrow 2}f(x)=f(2)=-3\)
Thus the required answers are
lim f(x) = -1
1-2-
lim f(x) = -1
1+2+
lim f(x) = -3
r2
f(2) = -3
Read more about functions here:
https://brainly.com/question/25638609
#SPJ1
Please help what is the slope of the line?
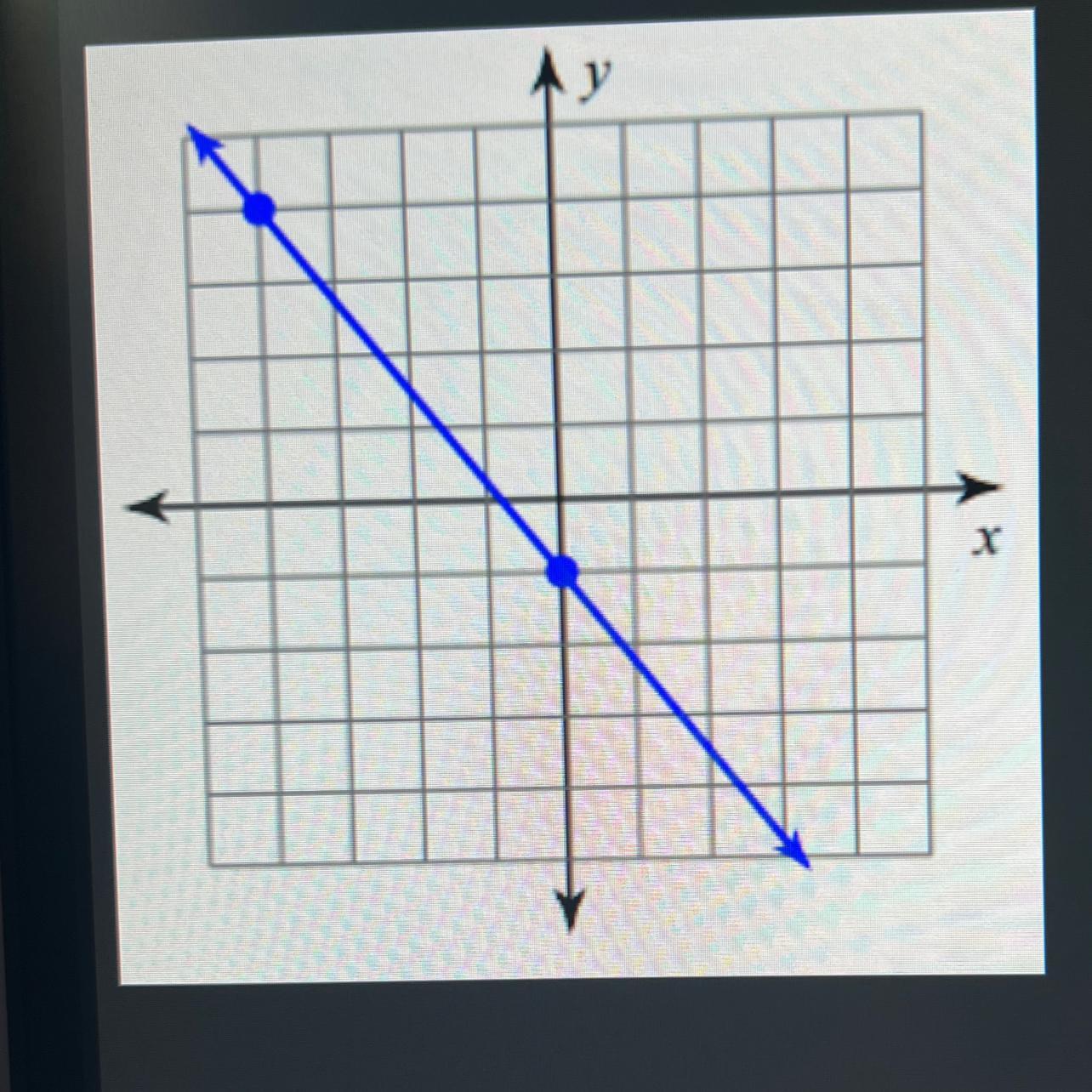
Answers
Answer:
-5/4
Step-by-step explanation:
Let \((x_1,y_1)=(-4,4)\) and \((x_2,y_2)=(0,-1)\). The slope of the line would be:
\(\displaystyle \frac{y_2-y_1}{x_2-x_1}=\frac{-1-4}{0-(-4)}=\frac{-5}{4}=-\frac{5}{4}\)
Answer: -5/4
Step-by-step explanation:
To find the slope between two points, you can use the formula:
Slope = (y2 - y1)/(x2 - x1)
Using the points (0, -1) and (-4, 4), we can substitute the coordinates into the formula:
slope = (4 - (-1))/(-4 - 0)
slope = (4 + 1)/(-4)
slope = 5/-4
Therefore, the slope between the two points is -5/4.
A process that fills plastic bottles with a beverage has a mean fill volume of 2.013 L and a standard deviation of 0.005 L. A case contains 18 bottles. Assuming that the bottles in a case are a simple random sample of bottles filled by this method, find the mean and standard deviation of the average volume per bottle in a case. studysoup
Answers
Answer:
Step-by-step explanation:
Given that
X1, X2, X3....... X18 are the volume of beverages in 18 bottles. These volumes have the same distribution and are independent of each other.
E.X(i) = 2.013L, while the Standard Deviation is given as
S D = X(i) = 0.005L
The average volume per bottle = X bar
E.X bar = E.X(i) = 2.013L
S D X bar = [S D X(i)]/√n = 0.005 /√18 = 0.005 / 4.24 = 1.18*10^-3L
Natalie can type 54 words per minute when transcribing an audio recording. Natalie needs to transcribe an audio recording with 7,938 words.
How many minutes will it take Natalie to transcribe the recording?
Enter your answer in the box.
min
Answers
Answer:
147 minutes (2 hours, 27 minutes)
Step-by-step explanation:
Help plz? I don’t know what to write

Answers
Answer:
1. C
2. B
3. A
4. D
Step-by-step explanation:
An element with a mass of 570 grams decays by 26.7% per minute. To the nearest minute, how long will it be until there are 40 grams of the element remaining?
Answers
Answer: x ≈ 9
Step-by-step explanation:
Near the end of the picture 8.553364=x
x ≈ 9

solve the following system of equations
1/2x+1/4y=-2
-2/3x+1/2y=6
x=
y=
Answers
Answer:
x = -6
y = 4
Step-by-step explanation:
Rewriting the equations :
2x + y = -84x - 3y = -36Now, solving the two equations using substitution method, we get :
x = -6
y = 4
Answer:
y = 4
x = -6
Step-by-step explanation:
1/2 x + 1/4 y= -2 first equation
-2/3 x + 1/2 y = 6 second equation
solution:
from the first equation:
8(1/2 x + 1/4 y) = -2*8
8x*1/2 + 8y*1/4 = -16
8x/2 + 8y/4 = -16
4x + 2y = -16 third equation
from the second equation
6(-2/3 x + 1/2 y) = 6*6
6x*-2/3 + 6y*1/2 = 36
-12x/3 + 6y/2 = 36
-4x + 3y = 36 fourth equation
from the third & fourth equation:
4x + 2y = -16
-4x + 3y = 36
0 + 5y = 20
5y = 20
y = 20/5
y = 4
from the fourth equation:
-4x + 3y = 36
-4x + 3*4 = 36
-4x + 12 = 36
-4x = 36 - 12
-4x = 24
x = 24/-4
x = -6
Check:
from the first equation:
1/2 x + 1/4 y = -2
1/2 *-6 + 1/4 * 4 = -2
-3 + 1 0 -2
from the second equation:
-2/3 x + 1/2 y = 6
-2/3 * -6 + 1/2 * 4 = 6
4 + 2 = 6
6x3 – 5x² + x + 1 divided by x + 2
Answers
Find the equation of a line that contains points (5,-3) and (-2,-4) in standard form
Answers
To find the equation of a line that passes through the points (5, -3) and (-2, -4) in standard form, we can use the point-slope form of a linear equation and then convert it to standard form.
Determine the slope (m) of the line using the formula:
m = (y2 - y1) / (x2 - x1)
For the given points (5, -3) and (-2, -4), we have:
m = (-4 - (-3)) / (-2 - 5) = (-4 + 3) / (-2 - 5) = -1 / (-7) = 1/7
Use the point-slope form of a linear equation:
y - y1 = m(x - x1)
Using the point (5, -3), we have:
y - (-3) = (1/7)(x - 5)
Simplifying:
y + 3 = (1/7)(x - 5)
Convert the equation to standard form:
Multiply both sides of the equation by 7 to eliminate the fraction:
7y + 21 = x - 5
Rearrange the equation to have the x and y terms on the same side:
x - 7y = 26
The equation of the line in standard form that passes through the points (5, -3) and (-2, -4) is x - 7y = 26.
For such more question on formula
https://brainly.com/question/29797709
#SPJ8
Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar.
A/60
B/45
C/105
The measurement of angle A is
The measurement of angle B is
The measurement of angle Cis
Answers
The second pair of points representing the solution set of the system of equations is (-6, 29).
To find the second pair of points representing the solution set of the system of equations, we need to substitute the x-coordinate of the second point into one of the equations and solve for y.
Given the system of equations:
y = x^2 - 2x - 19
y + 4x = 5
Substituting the x-coordinate of the second point (-6) into equation 2:
y + 4(-6) = 5
y - 24 = 5
y = 5 + 24
y = 29
Therefore, the second pair of points representing the solution set of the system of equations is (-6, 29).
for such more question on system of equations
https://brainly.com/question/4262258
#SPJ8
Question
Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar.
y = x2 − 2x − 19
y + 4x = 5
The pair of points representing the solution set of this system of equations is (-6, 29) and
_________.