peaches at the farmers market cost 2.70 per pound is it proportional
Answers
Related Questions
Interpret the results. Select the correct choice below and fill in the answer box to complete your choice. (Type an integer or a decimal. Do not round.) A. nothing% of all random samples of people from the population will have a mean driving distance to work (in miles) that is between the interval's endpoints. B. It can be said that nothing% of the population has a driving distance to work (in miles) that is between the interval's endpoints. C. With nothing% confidence, it can be said that most driving distances to work (in miles) in the population are between the interval's endpoints. D. With nothing% confidence, it can be said that the population mean driving distance to work (in miles) is between the interval's endpoints.
Answers
Answer:
With 99 % confidence, it can be said that the population mean driving distance to work (in miles) is between the interval's endpoints [19.91 miles, 31.49 miles] .
Step-by-step explanation:
The complete question is: In a random sample of six people, the mean driving distance to work was 25.7 miles and the standard deviation was 6.7 miles. Assuming the population is normally distributed and using the t-distribution, a 99% confidence interval for the population mean mu is left parenthesis 14.7 comma 36.7 right parenthesis (and the margin of error is 11.0).
Through research, it has been found that the population standard deviation of driving distances to work is 5.5 . Using the standard normal distribution with the appropriate calculations for a standard deviation that is known, find the margin of error and construct a 99 % confidence interval for the population mean mu .
Interpret the results. Select the correct choice below and fill in the answer box to complete your choice. (Type an integer or a decimal. Do not round.)
A. nothing % of all random samples of six people from the population will have a mean driving distance to work (in miles) that is between the interval's endpoints.
B. With nothing % confidence, it can be said that most driving distances to work (in miles) in the population are between the interval's endpoints.
C. It can be said that nothing % of the population has a driving distance to work (in miles) that is between the interval's endpoints.
D. With nothing % confidence, it can be said that the population mean driving distance to work (in miles) is between the interval's endpoints.
We are given that in a random sample of six people, the mean driving distance to work was 25.7 miles and the standard deviation was 6.7 miles.
Through research, it has been found that the population standard deviation of driving distances to work is 5.5 .
Firstly, the pivotal quantity for finding the confidence interval for the population mean is given by;
P.Q. = \(\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }\) ~ N(0,1)
where, \(\bar X\) = sample mean driving distance to work = 25.7 miles
\(\sigma\) = population standard deviation = 5.5 miles
n = sample of people = 6
\(\mu\) = population mean driving distance to work
Here for constructing a 99% confidence interval we have used a One-sample z-test statistics because we know about the population standard deviation.
So, 99% confidence interval for the population mean, \(\mu\) is ;
P(-2.58 < N(0,1) < 2.58) = 0.99 {As the critical value of z at 0.5% level
of significance are -2.58 & 2.58}
P(-2.58 < \(\frac{\bar X-\mu}{\frac{\sigma}{\sqrt{n} } }\) < 2.58) = 0.99
P( \(-2.58 \times {\frac{\sigma}{\sqrt{n} } }\) < \({\bar X-\mu}\) < \(2.58 \times {\frac{\sigma}{\sqrt{n} } }\) ) = 0.99
P( \(\bar X-2.58 \times {\frac{\sigma}{\sqrt{n} } }\) < \(\mu\) < \(\bar X+2.58 \times {\frac{\sigma}{\sqrt{n} } }\) ) = 0.99
99% confidence interval for \(\mu\) = [ \(\bar X-2.58 \times {\frac{\sigma}{\sqrt{n} } }\) , \(\bar X+2.58 \times {\frac{\sigma}{\sqrt{n} } }\) ]
= [ \(25.7-2.58 \times {\frac{5.5}{\sqrt{6} } }\) , \(25.7+2.58 \times {\frac{5.5}{\sqrt{6} } }\) ]
= [19.91, 31.49]
Therefore, a 99% confidence for the population mean is [19.91, 31.49] .
The margin of error here is = \(2.58 \times {\frac{\sigma}{\sqrt{n} } }\)
= \(2.58 \times {\frac{5.5}{\sqrt{6} } }\) = 5.793
With 99 % confidence, it can be said that the population mean driving distance to work (in miles) is between the interval's endpoints [19.91, 31.49] .
can someone please help

Answers
Answer:
The measure of CD is 46
Step-by-step explanation:
From the midpoint theorem, we have,
FG = (1/2)CD
so,
\(13+5x=(1/2)(-3x+52)\\So,\\2(13+5x)=-3x+52\\26+10x=-3x+52\\13x=52-26\\13x=26\\x=26/13\\x=2\)
Now,
\(CD = -3x+52\\since \ x=2\\we \ get\\CD=-3(2) +52\\CD=-6+52\\CD=46\)
Can anyone help please. Please show work too

Answers
The solutions to the system of equations are x = 2 and 4
How to determine the solution to the system of equationsFrom the question, we have the following parameters that can be used in our computation:
f(x) = x - 3
g(x) = 1/(x - 3)
The solution to the system of equations implies that
f(x) = g(x)
So, we have
x - 3 = 1/(x - 3)
Cross multiply the equation
This gives
(x - 3)² = 1
So, we have
x - 3 = ±1
Add 3 to both sides
x = 3 ± 1
So, we have
x = 2 and 4
Hence, the solutions to the system of equations are x = 2 and 4
Read more about equations at
https://brainly.com/question/148035
#SPJ1
Matrix Representation of Linear Regression Recall the linear regression problem from previous statistics class: Suppose that we observe 3 observations (Yi, x),(½, x2),(⅓,Xs) and they take values (0.3,1), (0.8,2), (-0.3,0.1).
Answers
The matrix representation of the problem can be written as: ε = [ε1 ε2 ε3]'
The matrix representation of the linear regression problem can be expressed as Y = Xβ + ε, where Y is the n x 1 vector of the dependent variable (Yi),
X is the n x k matrix of the independent variables (xi),
β is the k x 1 vector of coefficients, and
ε is the n x 1 vector of errors.
In this case, n = 3 (number of observations), k = 2 (number of independent variables) and the matrix representation of the problem can be written as:
Y = Xβ + ε
Y = [0.3 0.8 -0.3]
X = [1 1 1; 1 2 0.1]
β = [β0 β1]'
ε = [ε1 ε2 ε3]'
For more questions on Matrix representation
https://brainly.com/question/13594851
#SPJ4
help asap!! answer

Answers
Ali, Basti and Cian stand at three points A, B and C respectively. Suppose that the measure of angle ABC is 50 degrees , the measure of angle BAC is 60 degrees and Ali is exactly 150 ft away from Basti. Find the distance between Basti and Cian.
Answers
To find the distance between Basti and Cian, we can use the law of sines in triangle ABC. The law of sines states that the ratio of the length of a side to the sine of the opposite angle is constant for all sides and their corresponding angles in a triangle.
Let's label the distance between Basti and Cian as "x". We know that the measure of angle ABC is 50 degrees and the measure of angle BAC is 60 degrees. We also know that Ali is exactly 150 ft away from Basti.
Using the law of sines, we can set up the following equation:
sin(50°) / 150 = sin(60°) / x
To solve for "x", we can rearrange the equation:
x = (150 * sin(60°)) / sin(50°)
Using a calculator, we can evaluate the expression:
x ≈ (150 * 0.866) / 0.766
x ≈ 168.4 ft
Therefore, the distance between Basti and Cian is approximately 168.4 ft.
n over 4=1.2 answer me lol
Answers
Answer:
N = 5
Step-by-step explanation:
Answer:
n=5
Step-by-step explanation:
Out of 200 students in a senior class, 32 seniors are in the band and 64 seniors are in the band or on the honor roll. What is the probability that a randomly selected senior is both in the band and on the honor roll? Express your answer a fraction in simplest form.
Answers
The Probability that a randomly selected senior is both in the band and on the honor roll is 8/25.
To find the probability that a randomly selected senior is both in the band and on the honor roll, we need to divide the number of seniors who are in both categories by the total number of seniors.
Given:
Total number of seniors = 200
Number of seniors in the band = 32
Number of seniors in the band or on the honor roll = 64
Let's calculate the probability using these values:
Probability = Number of seniors in both categories / Total number of seniors
Probability = 64 / 200
To simplify this fraction, we can divide both the numerator and denominator by their greatest common divisor, which is 8:
Probability = (64 ÷ 8) / (200 ÷ 8)
Probability = 8 / 25
Therefore, the probability that a randomly selected senior is both in the band and on the honor roll is 8/25.
For more questions on Probability .
https://brainly.com/question/24756209
#SPJ8
What is the slope of this line?
4
−3
−3/4
3/4

Answers
Answer:
The answer is -3/4.
Answer: -3/4
Step-by-step explanation:
The line is pointing downwards, making it negative and having a negative slope. The line goes down 3, over 4, so its slope is -3/4.
It snowed 3 inches on Monday and 0.5 inches on Tuesday. How much did it snow on Monday and Tuesday combined?
Answers
Answer: It snowed 3.5 inches on Monday and Tuesday combined.
Step-by-step explanation: 3 + 0.5 = 3.5 inches of snow
Hope this helped!
I NEED HELP WITH STATISTICS

Answers
A. The null hypothesis H₀ and the alternative hypothesis H₁ are:
H₀: μ = 35 minutes H₁: μ > 35 minutes
B. If the consultant decides not to reject the null hypothesis, she might be making a Type II error.
C. A Type II error would be failing to reject the hypothesis that μ is = to 35 minutes when, in fact, μ is 43 minutes.
What is a Type II error?A Type II error occurs when the null hypothesis is false, but the test does not reject it.
In this case, the consultant would be concluding that the mean shopping time is 35 minutes, when in fact it is greater than 35 minutes.
Find more exercises on Type II error;
https://brainly.com/question/29689920
#SPJ1
whats the equation of a line that passes through point (-1,3) with slope of 1
Answers
The equation of the line that passes through the point (-1, 3) with a slope of 1 is y = x + 4.
To find the equation of a line that passes through the point (-1, 3) with a slope of 1, we can use the point-slope form of a linear equation.
The point-slope form of a linear equation is given by:
y - y1 = m(x - x1)
where (x1, y1) represents the coordinates of a point on the line, and m represents the slope of the line.
Using the given point (-1, 3) and slope 1, we substitute these values into the point-slope form equation:
y - 3 = 1(x - (-1))
Simplifying:
y - 3 = x + 1
Now, we can rewrite the equation in the standard form:
y = x + 4
Therefore, the equation of the line that passes through the point (-1, 3) with a slope of 1 is y = x + 4.
for such more question on line
https://brainly.com/question/1821791
#SPJ8
Jasmine has a circular swimming pool with a radius of 4.2 meters. What is the circumference of the pool?
Answers
The circumference of the pool is 26.38 meters
How to determine the circumference?The radius, r is given as:
r = 4.2
The circumference, C is calculated using:
\(C =2\pi r\)
This gives
C =2 * 3.14 * 4.2
Evaluate
C = 26.38
Hence, the circumference of the pool is 26.38 meters
Read more about circumference at:
https://brainly.com/question/14283575
#SPJ1
The function F is given in 3 equivalent forms.
Which form most quickly reveals the y intercept?
Look at image below
Part 2: what is the y intercept?

Answers
The form that most quickly reveals the y intercept is
B f(x) = 1/2 x² - 5x + 21/2The y intercept is (0, 21/2)
What is y-intercept?The y-intercept is the point where a function or a curve intersects the y-axis. In other words, it is the value of the dependent variable (y) when the independent variable (x) is equal to zero.
In the form, f(x) = 1/2 x² - 5x + 21/2 it is easier to see that eliminating x by plugging in 0 leaves 21/2 which is the y intercept
hence we can easily say that the y intercept is (0, 21/2)
Learn more about y-intercept at
https://brainly.com/question/10606087
#SPJ1
If h(x) = -2x + 6, find x if h(x) = 12.
Answers
\(-2x+6=12\\2x=-6\\x=-3\)
A total of 27 students are in your class. There are nine more males than females.
How many females are in your class?
Answers
You invested $4000 between two accounts paying 3% and 4% annual interest. If the total interest earned for the year was $130, how much was invested at each rate?
Answers
You invested $3000 at 3% annual interest rate, and the remaining amount of $4000 - $3000 = $1000 was invested at 4% annual interest rate.
Let's assume you invested an amount, x, at 3% annual interest rate. This means the amount invested at 4% annual interest rate would be $4000 - x.
To calculate the interest earned from the investment at 3%, we multiply x by 3% (0.03). Similarly, the interest earned from the investment at 4% is calculated by multiplying ($4000 - x) by 4% (0.04).
According to the given information, the total interest earned from both investments is $130. So we can set up the equation:
0.03x + 0.04($4000 - x) = $130
Simplifying the equation:
0.03x + 0.04($4000 - x) = $130
0.03x + $160 - 0.04x = $130
-0.01x = $130 - $160
-0.01x = -$30
x = -$30 / -0.01
x = $3000
Therefore, you invested $3000 at 3% annual interest rate, and the remaining amount of $4000 - $3000 = $1000 was invested at 4% annual interest rate.
for such more question on interest rate
https://brainly.com/question/29451175
#SPJ8
I do not remember how to solve this

Answers
Answer:
Your answer is correct
Step-by-step explanation:
Use the rules of exponents to simplify the expression.
(q⁶)²To raise a power to another power, multiply the exponents.
q⁶ˣ²Multiply 6 by 2.
q¹²The correct option is the third.
Skandarfind the slope of the tangent line to the curve y at x. then write the equation of this tangent line. question content area bottom part 1 the slope of the line tangent to the curve y at x is 36. part 2 the equation of the line tangent to the curve y at x is y minus y equals 36 (x minus 3 ).
Answers
the equation of the line tangent to the curve y at x = 3 is y = 36x - 102. The slope of the tangent line to the curve y at x = 3 is 36.
The equation of the line tangent to the curve y at x = 3 can be written using the point-slope form of a line, which is:
y - y1 = m(x - x1)
where m is the slope of the line, (x1, y1) is a point on the line, and m and (x1, y1) are known. In this case, m = 36 and (x1, y1) = (3, y). Substituting these values into the equation above, we get:
y - y = 36(x - 3)
y = 36x - 102
So the equation of the line tangent to the curve y at x = 3 is
y = 36x - 102.
To know more Tangent
https://brainly.com/question/4470346
#SPJ4
ab-c/d has a value of 24. write the values if :-
1- a, b, c, d are all positive.
2- a, b, c, d are all negative.
3- a, b, c, d are mixed of negative and positive.
WRITE ANSWERS FOR 1, 2 AND 3
Answers
The values of ab, b - c, and c/d are 6, -1, and 4 respectively when a = 2, b = 3, c = 4 and d = 1.Using BODMAS rule, we can simplify the given expression.ab - c/d = 24
Given ab-c/d has a value of 24.Now, we have to find the value ofab, b - c, and c/d.Multiplying d on both sides, we getd(ab - c/d) = 24dab - c = 24d...(1)Now, we can find the value of ab, b - c, and c/d by substituting different values of a, b, c and d.Value of ab when a = 2, b = 3, c = 4 and d = 1ab = a * b = 2 * 3 = 6.
Value of b - c when a = 2, b = 3, c = 4 and d = 1b - c = 3 - 4 = -1Value of c/d when a = 2, b = 3, c = 4 and d = 1c/d = 4/1 = 4Putting these values in equation (1), we get6d - 4 = 24dSimplifying, we get-18d = -4d = 2/9
For more such questions on BODMAS rule
https://brainly.com/question/28832666
#SPJ8
If a soup recipe yields 20 gallons, how many 5 fluid ounce portions will the recipe yield?
Answers
The total number of 512 portions will be made the recipe that contains 5 fluid ounces each.
The soup recipe gives 20 gallons.
As we know one gallon produces 128 fluid ounces.
There are 20 gallons produced.
So the number of fluid ounces produced will be 20*128= 2560
Given in the question each portion contains 5 fluid ounces.
Then there is a total of 2560 numbers of fluid ounces.
So the number of portions will be = number of fluid ounces/ number of fluid ounces in each portion= 2560/5= 512
Therefore the total number of 512 portions will be made the recipe that contains 5 fluid ounces each.
Learn more about gallon
here: https://brainly.com/question/19152962
#SPJ10
Find the sum or difference.
1. -80+77 =
2. 77 + 160 =
3. -64+ (-33) =
4. 104-(-92) =
5. -105-(-122) =
6. 185-(-154) =
7. -53-(-59) =
8. -6+ (-35) =
9. 15-(-26)-(-39) =
10. -93 +191+ (-179)
Find the product or quotient.
11. 60+ 12 =
12. -194+ (-2)=
13. 88 (-2) =
14. -12 10 =
15. -10 (-11) =
16. 90+ (-6)=
17. 3 (-59) =
18. -7 (-2) =
19. 100 (0) =
20.100/0=
Answers
After answering the presented question, we may conclude that the solution of the expressions are as follows.
what is expression ?In mathematics, you can multiply, divide, add, or subtract. An expression is constructed as follows: Number, expression, and mathematical operator A mathematical expression (such as addition, subtraction, multiplication, or division) is made up of numbers, variables, and functions. It is possible to contrast expressions and phrases. An expression or algebraic expression is any mathematical statement that has variables, integers, and an arithmetic operation between them. For example, the phrase 4m + 5 has the terms 4m and 5, as well as the provided expression's variable m, all separated by the arithmetic sign +.
the solution of the expressions are as follows -
-3237-97196173396-4152-8172-196-176-12011084-177140undefined (division by zero is undefined)To know more about expressions visit :-
https://brainly.com/question/14083225
#SPJ1
Two boards are placed end to end to make a walkway. One board is 6 feet 11 inches long, and the other board is 5 feet 7 inches long. How long is the walkway?
Write your answer in feet and inches. Use a number less than 12 for inches.
Answers
The walkway is 11 feet 6 inches long.
To find the length of the walkway, we need to add the lengths of the two boards.
The first board is 6 feet 11 inches long, which can be written as 6 + 11/12 feet using the fact that there are 12 inches in a foot.
The second board is 5 feet 7 inches long, which can be written as 5 + 7/12 feet.
Now we can add the lengths of the two boards:
6 + 11/12 feet + 5 + 7/12 feet
= 11 + 6/12 feet
=11 + 1/2 feet
Therefore, the walkway is 11 feet 6 inches long.
To learn more on Coordinate Geometry click:
brainly.com/question/27326241
#SPJ1
Question 4
1 pts
What is the midpoint of the segment containing the endpoints (-3.3) and
05.1:
Answers
Answer:
1, 2
Step-by-step explanation:
Given parameters;
Endpoints = (-3, 3) and (5, 1)
Unknown:
The midpoint of the segment = ?
Solution:
The midpoint between two endpoints is given as;
x\(_{m}\), y\(_{m}\) =( \(\frac{x_{1} + x_{2} }{2}\) , \(\frac{y_{1} + y_{2} }{2}\))
x and y are coordinates
x₁ = -3
x₂ = 5
y₁ = 3
y₂ = 1
x\(_{m}\), y\(_{m}\) = \(\frac{-3 + 5}{2}\), \(\frac{3+ 1}{2}\)
x\(_{m}\), y\(_{m}\) = 1, 2
the amount of paint needed to cover a wall is proportional to its area. the wall is rectangular and has an area of 6z2 6z square meters. factor this polynomial to find possible expressions for the length and width of the wall. (assume the factors are polynomials.)
Answers
On factoring the polynomial 6z² + 6z the values for length and width are obtained as 6z and z + 1.
What is a polynomial?
Polynomial is formed composed of the phrases Nominal, which means "terms," and Poly, which means "many." An expression that consists of variables, constants, and exponents that is combined using mathematical operations like addition, subtraction, multiplication, and division is referred to as a polynomial.
We can factor the polynomial 6z² + 6z by taking out the greatest common factor, which is 6z -
6z² + 6z = 6z(z + 1)
This means that the area of the wall is equal to 6z(z + 1) square meters. Since the area of a rectangle is given by the product of its length and width, we can write -
6z(z + 1) = length × width
Therefore, the possible expressions for the length and width of the wall are -
length = 6z
width = z + 1
or
length = z + 1
width = 6z
Both of these expressions give a product of 6z(z + 1), which is equal to the area of the wall.
We can switch the roles of length and width, so there are two possible expressions for the dimensions of the wall.
Therefore, the length is 6z and width is z + 1.
To learn more about polynomial from the given link
https://brainly.com/question/24662212
#SPJ1
make e the subject
e-5=2f
Answers
Answer:
e-5=2f
take '-5' to the other side where '2f' is
e=2f+5
1) Use the figure to answer the
following question.
What is the volume of the following figure?
9 cubic units
10 cubic units
20 cubic units
1 cubic unit

Answers
Answer:
10
Step-by-step explanation:
If you multiply the width with the length and height , you will get nine, then add that lonely brick on top to get ten
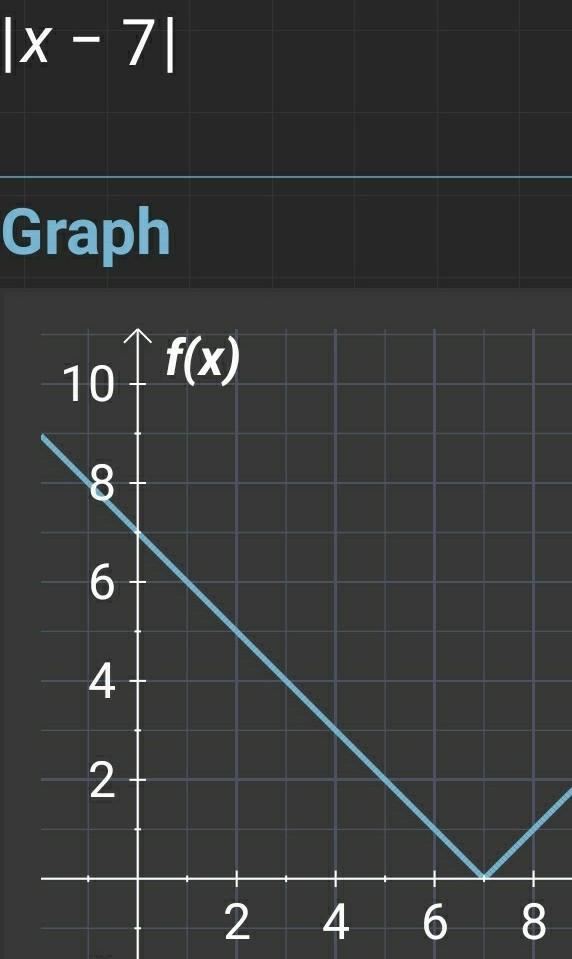
Solve:
|x-7|<-1.
zero solutions
one solution
infinite solutions
all real numbers
Answers
Step-by-step explanation:
In mathematics, the absolute value |x|, is the non-negative result of x without regard to its sign.
An absolute function, can never have a negative result.
By this alone, you can solve the question because the inequality is false, and therefore there are zero solutions.
Please see the attachment of f(x) = |x - 7|.
When you look at the graph, you can easily confirm that there is no value which can result in a negative y- coordinate like -2. In fact, that is the whole purpose of any absolute value or function. The result of an absolute function can never be negative.
Lucy spent 2 1/4 hour riding her bike. She then spent 3 3/4 hour playing video games. How much longer did she spend playing video games then riding her bike
Answers
Answer: 1 \(\frac{1}{2}\)
Step-by-step explanation: Turn the mixed fraction into improper fraction, which is 9/4 and 15/4. Subtract 15/4 and 9/4 to get 3/2. Convert 3/2 into mixed number to get 1 1/2
hope it helps!!
find the value of k if it is known that the line y=kx goes through the point B(-30,3)
Answers
Answer:
k = -0.1
Step-by-step explanation:
An ordered pair is in the form (x,y) We can use the x and y from the point (-30,3) to find k
y = kx We will replace x with -30 and y with 3
3 = (-30)k divide both sides by -30
-0.1 = k or \(\frac{-1}{10}\) in the fraction form