Perform the indicated operations. Express the result in scientific notation.
(5.7 x 105) + (4.6 x 106)-(2.9 x 105)
O 7.4 x 105
O 3.3 x 106
O 4.88 x 106
O 5.17 x 106
Answers
Answer:
The answer is C 4.88 x 106
Step-by-step explanation:
Related Questions
Note: Enter your answer and show all the steps that you use to solve this problem in the space provided.
Does the series converge or diverge? If it converges, what is the sum? Show your work.

Answers
Step-by-step explanation:
This is a geometric series where our common ratio is -1/2, and a is -4
Since r is less than -1, this series converges so
The sun is
\( \frac{ - 4}{1 + 0.5} \)
\( \frac{ - 4}{1.5} = - \frac{8}{3} \)
The sum is -8)3
estimate the sum by rounding off to nearest thousand 1784 + 4668
Answers
Answer:
6,000
Step-by-step explanation:
1784+4668=6452
6452 rounded to the nearest thousand is 6,000
which of the following is equivalent to x^2 -5x +6
Answers
Hello!
x² - 5x + 6
= (x² - 2x) + (-3x + 6)
= x(x - 2) - 3(x - 2)
= (x - 2)(x - 3)
Quadrilateral PQRS is transformed using the rule (x, y) - (x, y - 7). Which graph shows this transformation?




Answers
The transformed shape is made up of all the points from the original shape that have been shifted 7 units lower to their new places.
what is transformation ?A transformation in mathematics is the procedure of altering a geometric figure's position, size, or shape. Applying a set of rules, referred to as a transformation rule or transformation function, is how a transformation maps an initial figure to a new figure. Translation, rotation, reflection, and dilation are a few examples of transformations. Transformations are a crucial idea in geometry and are used in many areas of mathematics, such as topology, calculus, and linear algebra.
given
Every point in the initial shape will move 7 units downward according to the transformation formula (x, y) -> (x, y - 7). (in the negative y direction). As a result, the altered shape will be 7 units lower.
We can observe from the provided graphs that only the second graph exhibits the necessary transformation.
The transformed shape is made up of all the points from the original shape that have been shifted 7 units lower to their new places.
To know more about transformation visit :-
https://brainly.com/question/11709244
#SPJ1
For which pair of triangles could the Angle-Side-Angle Postulate (ASA) be used to prove that △ABC≅△XYZ ? I only have an hour pls help.

Answers
The pair that support Angle-Side-Angle Postulate (ASA) be used to prove that △ABC≅△XYZ is option B
What are congruent triangles?Triangles are said to be congruent when the sides and angles equal in accordance to to the triangle congruency rules
examples of these rules are
Angle - Side - Angle = ASASide - Side - Side = SSSSide - Angle - Side = SASAngle - Angle - Side = AASHypotenuse and one leg = HLThe problem requires the prove by Angle - Side- Angle = ASA to ensure that the the triangles are congruent
The Angle - Side - Angle = ASA have it that the two triangles being compared should have their two angles and the included side being equal
Learn more about congruent triangles here:
https://brainly.com/question/29393764
#SPJ1

the competitive advantage of some small american factories such as in tolerance contract manufacturing lies in their ability to produce parts with very narrow requirements, or tolerances, that are typical in the aerospace industry. consider a product with specifications that call for a maximum variance in the lengths of the parts of . suppose the sample variance for parts turns out to be . use , to test
Answers
The p-value is 0.1533, so p-value>0.05 fail to reject the null hypothesis. There is insufficient evidence to support the claim p-value greater than the significance level 0.05.
Consider the above given that
⇒\(& \alpha=0.05 \quad \mathrm{n}=34 \mathrm{~s}^2=0.0005 \\\)
⇒\(H_{0} : \sigma^2 \leq 0.0004 \\\)
⇒\(H_{a} : \sigma^2 > 0.0004\)
The null and alternative hypothesis test statistic:
Null and alternative hypotheses are used in statistical hypothesis testing. The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.⇒\(& \mathrm{x}^2=\left(\frac{\mathrm{n}-1}{\sigma^2}\right) \mathrm{s}^2 \\\)
\(& =\left(\frac{34-1}{0.0004}\right) 0.0005 \\\)
⇒\(& \mathrm{x}^2=\left(\frac{33}{0.004}\right) \times 0.0005 \\\)
\(& =82,500 \times 0.0005 \\\)
⇒\(& \mathrm{x}^2=41.25\)
⇒\(h_{0} : $\sigma^2$ is that or equal to $0.0004$\)
⇒\(h_{a} : $\sigma^2$ is greater that $0.0004$\)
⇒p value=p(z>41.25)
⇒p value=0.1533
By using P Value from Chi-Square Calculator
⇒p value=0.1533
⇒P value >0.05
Fail to reject the null hypothesis.
There is insufficient evidence to support the claim p value greater than the significance level 0.05.Therefore, the p-value is 0.1533, so p-value>0.05 fail to reject the null hypothesis.
For more such questions on null and alternative hypothesis
https://brainly.com/question/22334976
#SPJ4
The competitive advantage of some small Americans factories such as in tolerance contract manufacturing lies in their ability to produce parts with very narrow requirements, or tolerances, that are typical in the aerospace industry. consider a product with specifications that call for a maximum variance in the lengths of the parts of 0.0004. suppose the sample variance for 34 parts turns out to be \(s^{2}=0.0005\) . use \(\alpha=0.05\) , to test whether population variance specification is violated.
\(H_{0} \\H_{a}\)
Test statistic:
The p-value is-------.
the distance around a circle is called the
Answers
Answer:
circumference
Step-by-step explanation:
Question content area top
Part 1
Felix is slicing a tortilla Española (Spanish omelet) by cutting diameters through the center. He plans on cutting 1 to 8 diameters. The number of slices is a function of the number of diameters. Describe the domain and range of the function.
Answers
The function from which the number of slices can be found based on the number of diameters, can be obtained from the function, f(n) = 2·n, which indicates;
The domain = [1, 8]
The range = [2, 16]
What is the domain and range of a function?The domain is the set of the possible input of the function, while the range is the set of possible output of the function.
The number of diameters Felix plans to slice into the tortilla = 1 to 8
The number of arcs formed by a diameters of a circle = 2
The number of arcs formed by 8 diameters = 2 × 8
Therefore, the number of arcs formed by n diameters of a circle = 2·n
Each arc of the tortilla represents a slice, therefore:
The number of slices formed by n diameters = 2·n slices
The function of the number of slices Felix gets from cutting n number of diameters is; f(n) = 2·n
The domain is the possible number of inputs, which is the number of diameters, therefore;
The domain is; 1 ≤ n ≤ 8When n = 1, f(n) = f(1) = 2 × 1 = 2
When n = 8, f(8) = 2 × 8 = 16
The range is the possible number of slices obtained from the tortilla, therefore;
The range is; 2 ≤ f(n) ≤ 16Learn more about the domain and range of a function here:
https://brainly.com/question/1942755
#SPJ1
Not a Function
input
0
1
2
3
1
output
1
2
4
Function
Answers
Answer:
Not a Function
Step-by-step explanation:
there are 2 same inputs for different outputs
What would the height need to be for this curve to be a density curve?
1/5
1/4
1/2
1

Answers
For a curve to be a density curve, it must meet certain conditions such as it should be non-negative, and the area under the curve should equal 1. Furthermore, the curve should be continuous and smooth, and there should be no values outside the range of the data.
Let's see how the height would need to be for this curve to be a density curve.A density curve is a statistical representation of the distribution of a dataset or population. Density curves are used to describe the distribution of continuous data and provide a visual representation of the likelihood of an event occurring within a specific range of values. It helps to determine the proportion of data that falls within a given range of values. A density curve is used to provide a graphical representation of data without showing the individual data points.To be a density curve, a curve must have the following properties:The curve should be non-negative.The area under the curve should be equal to 1.The curve should be smooth and continuous.There should be no values outside the range of the data.From the above properties, we can conclude that the height required for a curve to be a density curve depends on the data that the curve represents. As long as the curve meets the above conditions, it can be considered a density curve. So, there is no specific height required for a curve to be a density curve. The height of the curve can vary depending on the range of the data and the distribution of the data.For such more question on properties
https://brainly.com/question/30339264
#SPJ8
A house has decreased in value by 38% since it was purchased. If the current value is $155,000, what was the value when it was purchased?
Answers
Is that the right question?
PLEASE LAST FEW SETS OF QUESTIONS FOR SEMESTER PLEASE HELP 2



Answers
Problem 1
Answer: C) 132.6--------------------
Explanation:
a1 = 1.7 = amount of concrete for the first step
a4 = x = amount of concrete for the fourth step
Sn = sum of the first n terms of an arithmetic sequence
Sn = (n/2)*(a1 + an)
S4 = (4/2)*(a1 + a4)
S4 = 2(1.7+x)
S4 = 2x+3.4
S4 = 17
2x+3.4 = 17
2x = 17-3.4
2x = 13.6
x = (13.6)/2
x = 6.8
We need 6.8 cubic feet of concrete for the fourth step. We'll use this value to help us find the common difference d
an = nth term of an arithmetic sequence
an = a1 + d(n-1)
a4 = a1 + d(4-1)
a4 = a1 + 3d
6.8 = 1.7 + 3d
6.8-1.7 = 3d
5.1 = 3d
(5.1)/3 = d
1.7 = d
d = 1.7
Coincidentally, the common difference is the same as the first term. This won't always happen.
Now we can compute the 12th term
an = a1 + d(n-1)
a12 = 1.7 + 1.7(12-1)
a12 = 20.4
which is then used to find the sum of the first 12 terms
Sn = (n/2)*(a1 + an)
S12 = (12/2)*(a1 + a12)
S12 = 6(1.7 + 20.4)
S12 = 132.6
=============================================================
Problem 2
Answer: C) \(x^2 + (y-10)^2 = 225\\\\\)--------------------
Explanation:
The center is (h,k) = (0,10) which is where the nozzle is located.
The distance from (0,10) to (0,25) is 15 units, so r = 15.
Also, the distance from (0,10) to (0,-5) is also 15 units.
Plug those values into the equation below.
\((x-h)^2 + (y-k)^2 = r^2\\\\(x-0)^2 + (y-10)^2 = 15^2\\\\x^2 + (y-10)^2 = 225\\\\\)
That equation represents the boundary of the circle, which is where the water can reach.
=============================================================
Problem 3
Answer: B) 2.336 ft--------------------
Explanation:
a1 = height 1st bounce = 6.7 fta2 = height 2nd bounce = 81% of a1 = 81% of 6.7 = 0.81*6.7 = 5.427a3 = height 3rd bounce = 81% of a2 = 81% of 5.427 = 0.81*5.427 = 4.39587Or note that,
a3 = 0.81*(a2) = 0.81*(0.81a1) = a1*(0.81)^2 = 6.7*(0.81)^2 = 4.39587
which must mean,
a4 = a1*(0.81)^3a5 = a1*(0.81)^4a6 = a1*(0.81)^5This is based off the idea that \(a_n = a(r)^{n-1}\)
So,
a6 = a1*(0.81)^5
a6 = 6.7*(0.81)^5
a6 = 2.33614554867
a6 = 2.336
At the beginning of a basketball season, the Panthers won 40 games out of 90 games. At this rate, how many games will they win in a normal 120-game season?
Answers
I’m actually not quite sure of this but what i did was 90-40= 50
120-50= 70
and it seems correct to me so
The following argument is an instance of one of the five inference forms MP, MT, HS, DS, Conj. Identify the form.
[(P ≡ T) • (H • N)] ⊃ (T ⊃ ~S)
(T ⊃ ~S) ⊃ [(H ∨ E) ∨ R]
[(P ≡ T) • (H • N)] ⊃ [(H ∨ E) ∨ R]
a. MP
b. DS
c. MT
d. Conj
e. HS
Answers
Answer:
e. HS
Step-by-step explanation:
The argument:
[(P ≡ T) • (H • N)] ⊃ (T ⊃ ~S)
(T ⊃ ~S) ⊃ [(H ∨ E) ∨ R]
[(P ≡ T) • (H • N)] ⊃ [(H ∨ E) ∨ R]
is an instance of one of hypothetical syllogism (HS).
Hypothetical syllogism contains conditional statements for its premises.
Let
p = [(P ≡ T) • (H • N)]
q = (T ⊃ ~S)
r = [(H ∨ E) ∨ R]
The this can be interpreted as:
p ⊃ q
q ⊃ r
p ⊃ r
This interprets that:
If p then q
but if q then r
therefore if p then r
Thus, in logic HS is a valid argument form:
p → q
q → r
∴ p → r
Note that ⊃ symbol is used to symbolize implication relationships. This is used in conditional statements which are represented in the if...then... form. For example p ⊃ q means: if p then q. So the type of Hypothetical syllogism used in this is conditional syllogism.
There are three parts of syllogism:
major premise
minor premise
conclusion
An example is:
If ABC is hardworking, then ABC will go to a good college.
Major premise: ABC is hardworking.
Minor premise: Because ABC is hardworking , ABC will score well.
Conclusion: ABC will go to a good college.
Example of Hypothetical syllogism:
If AB is a CD, then EF is a GH
if WX is a YZ, then AB is a CD
therefore if WX is a YZ, then EF is a GH
This can be understood with the help of an example:
If you study the topic, then you will understand the topic.
If you understand the topic, then you will pass the quiz.
Therefore, if you study the topic, then you will pass the quiz.
If a ring costs a jeweler $2100, at what price should it be sold to yield a profit of 50% on the selling price?
Answers
2100/2 = 1050
Meaning 50% is $1050
17. Rob purchased a boat three years ago. The boat decreased by 7% each year. Three years
later, the value of the boat was $32,174.28. Which equation initially models the value of Rob's
boat?
A. y = 40,000(0.93)*
B. y = 40,000(1.07)*
C. y = 32,174.28 (0.93)*
D. y = 32,174.28 (1.07)*
Answers
Answer:
The correct equation that initially models the value of Rob's boat is option A, y = 40,000(0.93)*.
Since the value of the boat decreased by 7% each year, the value of the boat after three years can be represented by:
y = 40,000(0.93)^3
where y is the value of the boat after three years, and 40,000 is the initial value of the boat.
Simplifying this equation, we get:
y = 40,000(0.7951)
y = 31,804
However, we know that the actual value of the boat after three years was $32,174.28. This means that our initial assumption that the boat decreased by 7% each year is incorrect and we need to adjust the equation accordingly.
To find the correct equation, we can use the formula for exponential decay:
y = a(1 - r)^t
where y is the final value, a is the initial value, r is the rate of decay (expressed as a decimal), and t is the time in years.
In this case, we know that the final value of the boat is $32,174.28, and that the boat was owned for three years. We also know that the value of the boat decreased by 7% each year.
So we can set up an equation:
32,174.28 = 40,000(0.93)^3
Simplifying this equation, we get:
32,174.28 = 31,804.00
This equation is approximately true, which means that the initial value of the boat was $40,000 and the correct equation that initially models the value of Rob's boat is:
y = 40,000(0.93)^t
where t is the time in years.
Which expressions are equivalent to 9b?
Choose all answers that apply
A. b+2(b+2b)
B. 3b+b
C. 2(2b)
Answers
Answer:
A. b+2(b+2b)
b + 2b + 4b = 7b
B. 3b + b = 4b
C. 2(2b) = 4b
None of them are equal to 9b
Answer:
\(\fbox {None}\)
Step-by-step explanation:
A
b + 2(b + 2b)b + 2(b) + 2(2b)b + 2b + 4b7bB
3b + b4bC
2(2b)4bI think I have the answer, but would like to check my work Find the area of the shape shown below
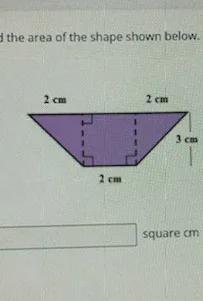
Answers
The figure contains two right angle triangles. The height is 3 cm and the base is 2 cm
The formula for determining the area of a triangle is
Area = 1/2 x base x height
Area of one triangle = 1/2 x 2 x 3 = 3 cm^2
Area of the two triangles = 3 x 2 = 6m^2
It also has a rectangle whose length is 3 cm and width is 2cm
Area of rectangle = 2 x 3 = 6 cm^2
The area of the figure = area of rectangle + area of both triangles. Thus,
Area of figure = 6 + 6 = 12 cm squared
Sophia pays a $25.00 membership fee for an online music store. If Sophia purchases n songs for
$3.00 each, and the total cost for her purchase is $60.00. Write and equation for the total cost
of songs s
Answers
Answer:
11 remainder 2 sorry if it's wrong...
Step-by-step explanation:
60.00- 25.00= 35.00 35.00 ÷ 3 = 11 r2
Help with this question!Please
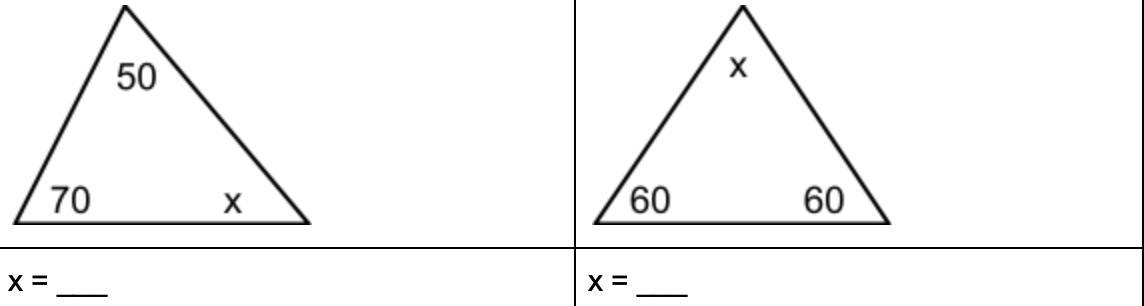
Answers
For both answers X= 60
\({\large\begin{gathered} { \underbrace{\boxed { \rm {\blue {Concept \: \: Using}}}}}\end{gathered}}\)
The angle sum property of a triangle:
Angle sum property of triangle states that the sum of interior angles of a triangle is 180°
\( \underline {\mathcal {{{\color{orange}{\bf \large \rightarrow \: \angle \: 1 \: + \: \angle \: 2 \: + \: \angle \: 3 \: = \: 180 \degree}}}}} \)
\({\large\begin{gathered} { \underbrace{\boxed { \rm {\blue {Solution}}}}}\end{gathered}}\)
In 1st Triangle ∠1 = 50°∠2 = 70°∠3 = x.
\(\bf \large\longrightarrow \: \: 50 \degree \: + \: 70 \degree \: + \: x \: = \: 180 \degree\)
\(\bf \large\longrightarrow \: \:120 \degree \: + \: x \: = \: 180 \degree\)
\(\bf \large\longrightarrow \: \: x \: = \: 180 \degree \: - \: 120 \degree\)
\(\bf \large\longrightarrow \: \: x \: = \: 60\degree\)
_______________________In 2nd Triangle∠1 = x∠2 = 60°∠3 = 60°\(\bf \large\longrightarrow \: \: x \: + \: 60 \degree \: + \: 60 \degree \: = \: 180 \degree\)
\(\bf \large\longrightarrow \: \: x \: + \: 120 \degree \: = \: 180 \degree\)
\(\bf \large\longrightarrow \: \: x \: = \: 180 \degree \: - \: 120 \degree\)
\(\bf \large\longrightarrow \: \: x \: = \: 60\degree\)
PEOPLE SHOW ANSWERS PLEASE AND WILL GIVE BRAINLIEST 8. The ratio of cats to dogs at a pet show
is 1:3.
a) What percent of the pets at the
show are cats?
Answers
Answer:
33.33%
Step-by-step explanation:
Answer:
1/4
Step-by-step explanation:
so we add 1 and 3 together becuase since there are equal parts, we need to add to get the whole. so since the ration is 1:3, there are 1/4x cats thereate the show
Which tables represents a function?
Select two answers.
Help

Answers
Answer:
I think B and C is the answer.
What is −5/6÷9/10?
−27/25
−4/3
−25/27
−3/4
Answers
Answer:
-25/27
Step-by-step explanation:
Answer:
\( - \frac{ 25}{27} \)
Step-by-step explanation:
\( - \frac{5}{6} \div \frac{9}{10} \\ - \frac{5}{6} \times \frac{10}{9} \\ \frac{ - 50}{54} \\ \frac{ - 50 \div 2}{54 \div 2} \\ \frac{ - 25}{27} \)
X S2.0.2
A rocket is fired upward with an initial velocity v of 80 meters per second. The quadratic function S(t) = -52 + 80t can be used to find
the heights of the rocket, in meters, at any time t in seconds. Find the height of the rocket 8 seconds after it takes off. During the
course of its flight, after how many seconds will the rocket be at a height of 290 meters?
Answers
9514 1404 393
Answer:
320 m after 8 seconds5.6 seconds, 10.4 seconds to height of 290 mStep-by-step explanation:
To find the height at 8 seconds, evaluate the formula for t=8.
S(t) = -5t^2 +80t
S(8) = -5(8^2) +80(8) = -320 +640 = 320
The height of the rocket is 320 meters 8 seconds after takeoff.
__
To find the time to 290 meters height, solve ...
S(t) = 290
290 = -5t^2 +80t
-58 = t^2 -16t . . . . . . . divide by -5
6 = t^2 -16t +64 . . . . . complete the square by adding 64
±√6 = t -8 . . . . . . . . . take the square root
t = 8 ±√6 ≈ {5.551, 10.449}
The rocket is at 290 meters height after 5.6 seconds and again after 10.4 seconds.

Let Xi = (i =1,2,3) be independently and normally distributed random variable with mean of 4 as variance i. state the distribution of the following random variable
i) V = X1+X2+X3
Answers
The sum of normally distributed random variables is also a normally distributed random variable.
Given \(n\) random variables with \(X_i\sim\mathrm{Normal}(\mu_i,\sigma_i^2)\), their sum is
\(\displaystyle\sum_{i=1}^n X_i \sim \mathrm{Normal}\left(\sum_{i=1}^n \mu_i, \sum_{i=1}^n \sigma_i^2\right)\)
i.e. normally distributed with mean and variance equal to the sums of the means and variances of the \(X_i\).
In this case, each of \(X_1,X_2,X_3\) are normally distributed with \(\mu=4\) and \(\sigma^2\) = ... I'm not sure what you meant for the variance, so I'll keep it symbolic. Then
\(V = X_1+X_2+X_3 \sim \mathrm{Normal}(12, 3\sigma^2)\)
Alex and Jose are working on some math problems.
Alex said 20 = 1 and 51 = 5.
Jose said 2° = 0 and 51 = 1.
-
-
Who is right and why?
Answers
Answer:
Alex is right so the problem is solved
A car’s gas tank will hold 24 gallons when full. The car’s tank is presently 1/3 full. How much more gas will it take to fill the tank?
Answers
The additional gas it will take to fill the tank is 16 gallons
How much more gas will it take to fill the tank?From the question, we have the following parameters that can be used in our computation:
Capacity = 24 gallons
Current volume = 1/3 full
This means that
Remaning volume = 1 - 1/3
Evaluate
Remaning volume = 2/3
The additional gas it will take to fill the tank is
Additional = 2/3 * 24
Evaluate
Additional = 16
Hence, the additional gas it will take to fill the tank is 16 gallons
Read more about proportion at
https://brainly.com/question/12024093
#SPJ1
What percent of 9 is 18?
Answers
Answer:
the answer is 50%
BRAINLIST
On a test, for every correct answer the student gets 2 points and for every
incorrect answer the student loses 1 point
Corinne got the first two questions correct and missed the next three.
She will receive a grade of zero if she answers
O
question(s)
correctly
incorrectly
# 1
correctly
incorrectly
Answers
Answer: she will receive a grade of zero if she gets one more question incorrect.
Step-by-step explanation: She gets 2 questions correct which equals 4 points and 3 questions wrong which is minus 3 points
4-3=1 so if she were to get one more incorrect she would receive a zero
If a person drives a car in the United States, that person must drive on the right side of the road. Kaylee drives a car in the United States.
A. Kaylee has her driver's license.
B. Kaylee must drive on the left side of the road.
C. Kaylee must drive on the right side of the road.
D. Kaylee must park her car on the right side of the road.