Answers
Answer:
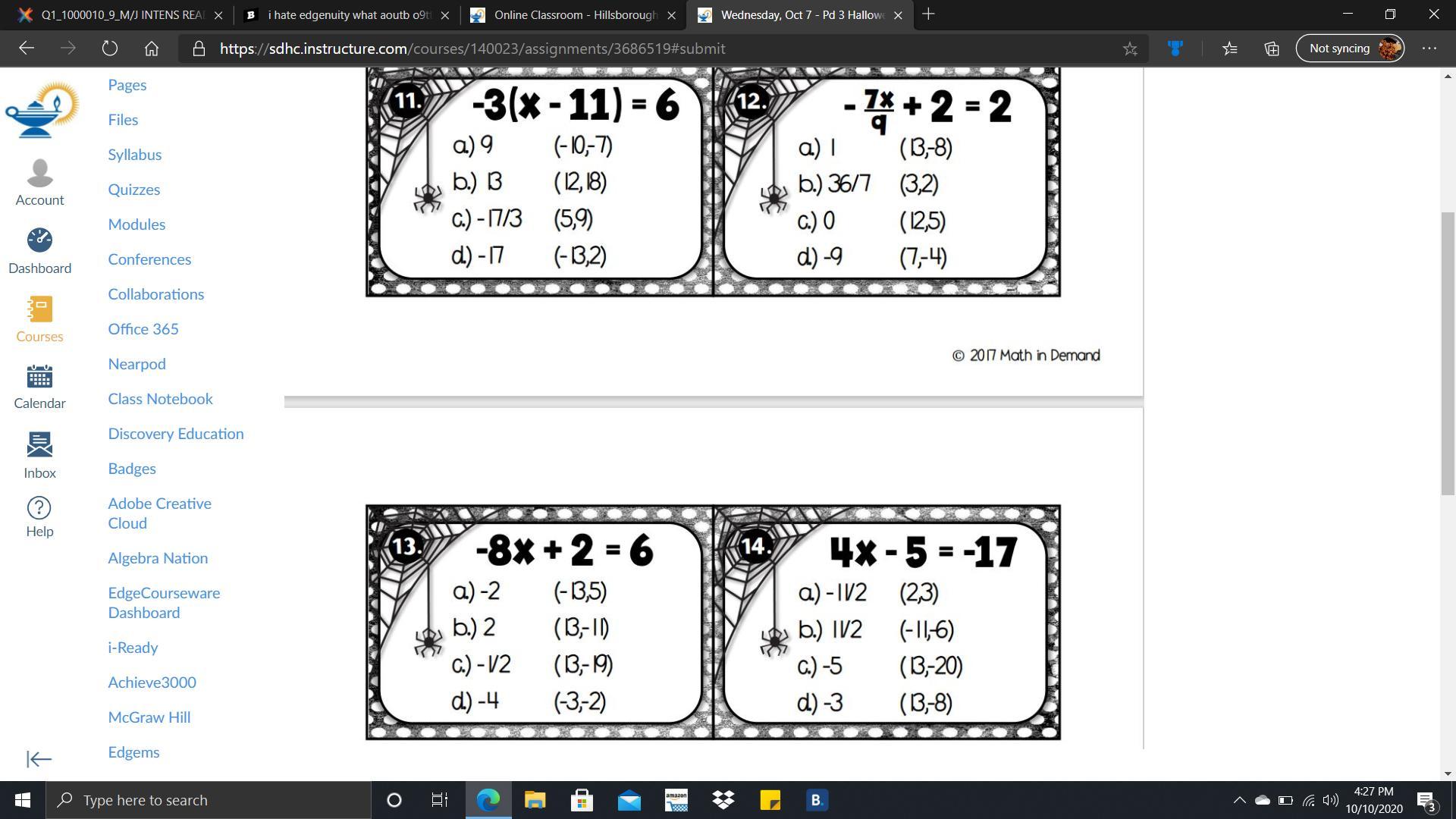
11. a) 912. c) 013. c) -1/214. d) -3Step-by-step explanation:
11.
-3(x - 11) = 6x - 11 = -2x = 11 - 2x = 912.
-7x/9 + 2 = 2-7x/9 = 0x = 013.
-8x + 2 = 6-8x = 4x = 4/(-8)x = -1/214.
4x - 5 = -174x = 5 - 174x = -12x = -12/4x = -3Related Questions
round 420000 to the nearest tenth
Answers
Answer:
It is rounded
Step-by-step explanation:
Answer:
It is already rounded up, unless you have forgotten the decimal point.
Step-by-step explanation:
given the diagram below, what is COS(45º)?

Answers
Answer:
1 / \(\sqrt{2}\)
Step-by-step explanation:
In a 45,45,90 triangle, the two legs of the triangle are equal to each other and the hypotonus being x \(\sqrt{2}\). So that make the unknown sides 6 and 6\(\sqrt{2}\). When solving for cos(45) you divide the leg adjacent to the 45 (6) by the hypotonus (6\(\sqrt{2}\)) This gives you 6/6\(\sqrt{2}\). You can simplify the 6s to get 1 / \(\sqrt{2}\)
Explanation:
This is a 45-45-90 right triangle, aka isosceles right triangle.
The two legs are 6 units each, because the legs of isosceles triangles are the same length.
The hypotenuse is 6*sqrt(2) through the use of the pythagorean theorem.
From here we can say:
\(\cos\left(\text{angle}\right) = \frac{\text{adjacent}}{\text{hypotenuse}}\\\\\cos\left(45^{\circ}\right) = \frac{6}{6\sqrt{2}}\\\\\cos\left(45^{\circ}\right) = \frac{1}{\sqrt{2}}\\\\\)
It turns out that the '6' has nothing to do with the final answer, since the '6's cancel out. So we could change that 6 to any number we want, and the answer would still be the same.
Side note: Rationalizing the denominator will have \(\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
Find the Value
A.
B.
C.
D.

Answers
Answer:
C
Step-by-step explanation:
Using the trig. identity
sin²x + cos²x = 1 ⇒ cosx = ± \(\sqrt{1-sin^2x}\)
Here sinθ = \(\frac{1}{2}\) , thus
cosθ = ± \(\sqrt{1-(\frac{1}{2})^2 }\) = ± \(\sqrt{1-\frac{1}{4} }\) = ± \(\sqrt{\frac{3}{4} }\) = ± \(\frac{\sqrt{3} }{2}\)
Since 0 ≤ θ > 90 then cosθ > 0 , thus
cosθ = \(\frac{\sqrt{3} }{2}\) → C
Select all the true statements:
A) Two squares with the same side lengths are always congruent
B) Two rectangles with the same side lengths are always congruent
C) Two rhombuses with the same side lengths are always congruent
D) Two parallelograms with the same side lengths are always congruent
E) Two quadrilaterals with the same side lengths are always congruent
Answers
Answer:
A and C
Step-by-step explanation:
A) Two squares with the same side lengths are always congruent
C) Two rhombuses with the same side lengths are always congruent.
Two geometric shapes are called congruent if they have the same size and the same shape.
A square has all four sides equal, therefore two squares with the same side lengths are always congruent in all respect (shape and area). Two rhombuses with the same side lengths are always congruent. Two rectangles are congruent if both of them have the opposite sides are equal. Two parallelograms are said to be congruent if all four corresponding sides are equal in length & one corresponding internal angle is equal.Therefore the true statements are A and C.
Learn more:https://brainly.com/question/22982385
Alice's mother wants to wallpaper two adjacent walls in Alice's bedroom. She also wants to put a border along the top of all four walls. The bedroom is 9 ft by 12 ft by 8 ft high. A) If each double roll covers approximately 60 fr and the wallpaper is sold in double rolls only, how many double rolls are needed? B) If the border is sold in rolls of 5 yd each, how many rolls of the border are needed?
Answers
Answer:
A) The number of wallpapers needed to cover the walls is 6 double roll wall papers
B) The number of wall paper border rolls needed is 3 rolls
Step-by-step explanation:
A) The given parameters are;
The dimensions of the room are 9 ft. by 12 ft. by 8 ft. high,
The area one double role wallpaper covers = 60 ft.²
Therefore, we have;
The area of the room wall = 12 × 8 × 2 + 9 × 8 × 2 = 336 ft²
The number of double rolls of wallpaper to be used = Area of wall/(area of wallpaper) = 336/60 = 5.6
Therefore, given that the wall papers are sold in single units, we round up to the next whole number of units to get;
The number of wallpapers needed to cover the walls = 6 double roll wall papers
B) The borders of a wallpaper are installed parallel (and installed along) to the ceiling line
Therefore, the amount of wallpaper border required is given as follows;
Wall paper border length required = 2 × Length of the room + 2 × Width of the room
∴ Wall paper border length required = 2 × 9 ft. + 2 × 12 ft. = 42 ft.
The size of each wall paper border sold = 5 yd. = 15 ft.
Therefore;
The number of wall paper border rolls required = 42 ft./(5 yd.) = 42 ft./(15 ft.) = 2.8 rolls
Therefore, we round up to get the number of wall paper border rolls needed as 3 rolls of wall paper borders.
Which ratio in the form A:B is equivalent to the ratios in
the table?
2
3
B
12
18
24
30
O 6:35
O 7:40
O 8:48
O 9:63

Answers
Answer:
3rd option : 8:48
Step-by-step explanation:
every number in the B row divided its A is 6
3rd option : 48 divided by 8 is 6
Find the inequality represented by the graph

Answers
Answer:
y < 1/4x + 3
Step-by-step explanation:
the line is dotted so we know the symbol will not include the "equal to" part
we can also see that the shading in below the y intercept, so we know that the symbol will also be less than
this means the symbol is <
now, create an equation for the line:
we know that the y intercept is 3, and that there is a rise of 1 and a walk of 4
so the slope is 1/4
now put this together and you get 1/4x + 3
this part will go on the right side of the < symbol in your inequality
so now you can create an inequality: y < 1/4x + 3
Answer:
y < \(\frac{1}{4}\) x + 3
Step-by-step explanation:
m = \(\frac{1}{4}\) and coordinates of y-intercept are (0, 3)
y < \(\frac{1}{4}\) x + 3
determine the interval of convergence for the taylor series off (x) = at x x = 1. write your answer in interval notation.
Answers
The interval of convergence for the given Taylor series of f(x) = aₙ(x − 1)ⁿ at x = 1 is (-∞, ∞), which can be written in interval notation as (-∞, ∞)
To determine the interval of convergence for the given Taylor series of f(x) = aₙ(x − 1)ⁿ, we can make use of the ratio test. The ratio test is a test that can be used to test whether an infinite series converges or diverges.
The formula for the nth term of the given Taylor series of f(x) is given by:
aₙ = fⁿ(1) / n! × (x − 1)ⁿ
Given that
f(x) = aₙ(x − 1)ⁿ,
we can conclude that:
fⁿ(1) = n! × aₙ
Therefore, the nth term of the Taylor series of f(x) can be written as
aₙ = aₙ / (x − 1)ⁿ
Since we need to determine the interval of convergence for the given Taylor series of f(x), we can make use of the ratio test. According to the ratio test, the series converges if:
limₙ→∞ |aₙ₊₁ / aₙ| < 1
Therefore, we can write:
|aₙ₊₁ / aₙ| = |aₙ₊₁ / aₙ| × |(x − 1) / (x − 1)|= |(n + 1) × aₙ₊₁ / aₙ| × |(x − 1)|
Since we need to find the interval of convergence for the given Taylor series of f(x), we can assume that the series converges. Therefore, we can write:
limₙ→∞ |(n + 1) × aₙ₊₁ / aₙ| × |(x − 1)| < 1
Therefore, we can write:
limₙ→∞ |aₙ₊₁ / aₙ| = |(n + 1) × aₙ₊₁ / aₙ| × |(x − 1)| < 1|x − 1| < 1 / limₙ→∞ |(n + 1) × aₙ₊₁ / aₙ|
The limit on the right-hand side of the above inequality can be evaluated by making use of the ratio test. Therefore, we can write:
limₙ→∞ |aₙ₊₁ / aₙ| = limₙ→∞ |(n + 1) × aₙ₊₁ / aₙ|= limₙ→∞ |n + 1| × |aₙ₊₁ / aₙ|= LIf L < 1, then the given Taylor series of f(x) converges. Therefore, we can write:|x − 1| < 1 / L
Also, we need to find the value of L.
Since the given Taylor series of f(x) is centered at x = 1, we can assume that a₀ = f(1) = a and that fⁿ(1) = n! × a, for all n ≥ 1.
Therefore, the nth term of the given Taylor series of f(x) can be written as:
aₙ = aₙ / (x − 1)ⁿ= a / (x − 1)ⁿ
Since we need to find the value of L, we can write:
L = limₙ→∞ |(n + 1) × aₙ₊₁ / aₙ|
= limₙ→∞ |n + 1| × |aₙ₊₁ / aₙ|
= limₙ→∞ |n + 1| × |a / (n + 1)(x − 1)|
= |a / (x − 1)| × limₙ→∞ |1 / n + 1|
Since,
limₙ→∞ |1 / n + 1| = 0,
we can write:
L = |a / (x − 1)| × 0= 0
Therefore, we can write:
|x − 1| < 1 / L= 1 / 0= ∞
Therefore, the interval of convergence for the given Taylor series of f(x) is given by:[1 - ∞, 1 + ∞] = (-∞, ∞)
To know more about Taylor series, visit:
https://brainly.com/question/31140778
#SPJ11
Wilson began watering his garden with a watering can that was completely full. The amount of water in the can as Wilson was watering can be represented by a linear function and is shown in the graph below. Which statement is correct

Answers
Answer:
B. The amount of water originally in Wilson's can was 2.5 gallons.
A family of 4 gets 505 text messages per month. Which of the following best describes the most even way these texts can be divided?
2 family members get 124 text messages each
2 family members get 125 text messages each
2 family members get 126 text messages each
2 family members get 125 text messages each
3 family members get 126 text messages each
1 family member gets 127 text messages
3 family members get 125 text messages each
1 family member gets 126 text messages
Answers
Answer:
3 family members get 126 text messages each
1 family member gets 127 text messages
Step-by-step explanation:
If you were finding the exact division of texts, 505 texts / 4 people, you would end up with 126.25 texts.
However, you can't get 0.25 of a text. If we take back each family member's 0.25 text, they will all be left with 126 texts (with an extra text leftover)
This extra text is considered the "remainder", meaning the amount left over when a number is divided [when it doesn't go into the larger number evenly]. The only importance/relevancy of a remainder is when a value cannot be split, such as a dog or a text.
So, we can give each family member 126 texts, and then we can give one family member an additional text, so that all texts are distributed.
This means that 3 family members get 126 texts, and 1 family member gets 127 texts
hope this helps!!
A mathematician is wondering what would happen to the surface area of a square if you were to repeatedly cut the square in half. She concludes that the surface area would become less and less but would never become zero units\(^2\). Which equation would help her model the surface area of a square piece of paper as it was repeatedly cut?
a) \(y=x^2+4x-16\)
b) \(y=-25x^2\)
c) \(y=9(2)^x\)
d) \(y=36(\frac{1}{2})^x\)
Answers
The equation that would help the mathematician model the surface area of a square piece of paper as it was repeatedly cut is \(y = 36 \times \frac{1}{2}^x\)
Option D is the correct answer.
We have,
In this equation, the variable x represents the number of times the square is cut in half, and y represents the surface area of the square.
As x increases, the exponent of 1/2 decreases, causing the value of y to decrease.
This exponential decay accurately represents the idea that the surface area becomes less and less but never reaches zero units²
Thus,
The equation that would help the mathematician model the surface area of a square piece of paper as it was repeatedly cut is \(y = 36 \times \frac{1}{2}^x\).
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ1
The correct equation that would help model the surface area of a square piece of paper as it is repeatedly cut in half is: \(\(y=36(\frac{1}{2})^x\)\)
As the square is cut in half, the side length of the square is divided by 2, resulting in the area being divided by \(\(2^2 = 4\)\).
Therefore, the equation \(y=36(\frac{1}{2})^x\)\)accurately represents the decreasing surface area of the square as it is repeatedly cut in half.
and, \(\(y=x^2+4x-16\)\)is a quadratic equation that does not represent the decreasing nature of the surface area.
and, \(\(y=-25x^2\)\) is a quadratic equation with a negative coefficient.
and, \(\(y=9(2)^x\)\)represents exponential growth rather than the decreasing nature of the surface area when the square is cut in half.
Learn more about Equation here:
https://brainly.com/question/29657983
#SPJ1
An amusement park has plans to install a free pop-up game booth during slower summer days. Previous experience indicates that, on average, 10 persons per hour will use the booth. Assume arrivals are Poisson distributed from an infinite population. The game takes a constant time of five minutes per player. Assume the queue length can be infinite with FCFS discipline.
What average number in line can be expected?
What average number of persons can be expected to be in the system?
What is the average amount of time that a person can expect to spend in line?
On some days, the arrival rate can be expected to increase to over 12 per hour. What effect will this have on the number in the waiting line?
Answers
The average number in line: 0.5 persons. Average number of persons in the system: 1 person. Average time spent in line: 2.5 minutes. Increased arrival rate will result in more people in the waiting line.
The average number in line can be calculated using the formula for the average number of customers in the system, Ls = λWs, where λ is the arrival rate and Ws is the average time a customer spends in the system. In this case, the arrival rate is 10 persons per hour and the time per player is 5 minutes. Converting the arrival rate to arrivals per minute, we have λ = 10/60 = 1/6 arrivals per minute. Plugging these values into the formula, we get Ls = (1/6) * 5 = 5/6 = 0.833, which can be approximated to 0.5 persons.
The average number of persons expected to be in the system includes both those in the line and those being served. Since the system follows a First-Come-First-Serve (FCFS) discipline, the number of people in line will be equal to the number of people in the system. Therefore, the average number of persons in the system is also 0.5 persons.
The average amount of time a person spends in line can be calculated using Little's Law, which states that the average number of customers in a stable system is equal to the arrival rate multiplied by the average time a customer spends in the system. In this case, the average number of customers in the system is 0.5 persons and the arrival rate is 10 persons per hour. Converting the arrival rate to arrivals per minute, we have λ = 10/60 = 1/6 arrivals per minute.
Plugging these values into the formula, we get 0.5 = (1/6) * Ws. Solving for Ws, we find Ws = 3 minutes. Since the average time spent in the system includes both waiting time and service time, and the service time is 5 minutes per player, the average time spent in line is Ws - service time = 3 - 5 = -2 minutes. However, a negative waiting time is not meaningful in this context. Therefore, we can approximate the average time spent in line to 2.5 minutes.
Learn more about average
brainly.com/question/24057012
#SPJ11
1. Consider the random variable X with two-sided exponential distribution given by fx(x)= -|x| e- (a) Show that the moment generating function of X is My(s) že-1x1 the mean and variance of X. (b) Use Chebychev inequality to estimate the tail probability, P(X> 8), for 8 >0 and compare your result with the exact tail probability. (c) Use Chernoff inequality to estimate the tail probability, P(X> 8), for 8> 0 and compare your result with the CLT estimate of the tail of the probability, P(X> 8), for 8 >0. and, hence or otherwise, find
Answers
(a) To find the moment generating function (MGF) of X, we use the definition of the MGF:
My(s) = E(e^(sX))
First, let's find the probability density function (pdf) of X. The given pdf is:
fx(x) = -|x| * e^(-|x|)
To find the MGF, we evaluate the integral:
My(s) = ∫e^(sx) * fx(x) dx
Since the pdf fx(x) is defined differently for positive and negative values of x, we split the integral into two parts:
My(s) = ∫e^(sx) * (-x) * e^(-x) dx, for x < 0
+ ∫e^(sx) * x * e^(-x) dx, for x ≥ 0
Simplifying the integrals:
My(s) = ∫-xe^(x(1-s)) dx, for x < 0
+ ∫xe^(-x(1-s)) dx, for x ≥ 0
Integrating each part:
My(s) = [-xe^(x(1-s)) / (1-s)] - ∫-e^(x(1-s)) dx, for x < 0
+ [xe^(-x(1-s)) / (1-s)] - ∫e^(-x(1-s)) dx, for x ≥ 0
Evaluating the definite integrals:
My(s) = [-xe^(x(1-s)) / (1-s)] + e^(x(1-s)) + C1, for x < 0
+ [xe^(-x(1-s)) / (1-s)] - e^(-x(1-s)) + C2, for x ≥ 0
Applying the limits and simplifying:
My(s) = [-xe^(x(1-s)) / (1-s)] + e^(x(1-s)) + C1, for x < 0
+ [xe^(-x(1-s)) / (1-s)] - e^(-x(1-s)) + C2, for x ≥ 0
To find the constants C1 and C2, we consider the continuity of the MGF at x = 0:
lim[x→0-] My(s) = lim[x→0+] My(s)
This leads to the equation:
C1 + C2 = 0
Taking the derivative of My(s) with respect to x and evaluating at x = 0, we find the mean of X:
E[X] = My'(0)
Similarly, taking the second derivative of My(s) with respect to x and evaluating at x = 0, we find the variance of X:
Var(X) = E[X^2] - (E[X])^2 = My''(0) - (My'(0))^2
(b) To estimate the tail probability P(X > 8) using Chebyshev's inequality, we use the variance calculated in part (a).
Chebyshev's inequality states that for any positive constant k:
P(|X - E[X]| ≥ kσ) ≤ 1/k^2
In our case, we want to estimate P(X > 8), so we can rewrite it as P(X - E[X] > 8 - E[X]).
Let k = (8 - E[X]) / σ, where E[X] is the mean calculated in part (a) and σ is the square root of the variance calculated in part (a).
Then, P(X > 8) = P(X - E[X] > 8 - E[X]) ≤ 1/k^2
(c) To estimate the tail probability P(X > 8) using Chernoff's inequality, we need to find the moment generating function (MGF) of X.
The Chernoff bound states that for any positive constant t:
P(X > a) ≤ e^(-at) * Mx(t)
Where Mx(t) is the MGF of X.
Using the MGF derived in part (a), substitute t = 8 and calculate Mx(t). Then use the inequality to estimate P(X > 8).
To compare the result with the Central Limit Theorem (CLT) estimate of the tail probability P(X > 8), you need to find the CLT estimate for the given distribution. The CLT approximates the distribution of a sum of independent random variables to a normal distribution when the sample size is large enough.
The CLT estimate for P(X > 8) involves standardizing the distribution and using the standard normal distribution to calculate the tail probability.
By comparing the results from Chernoff's inequality and the CLT estimate, you can observe the differences in the estimated tail probabilities for X > 8.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
the number of traffic accidents per week in a small city has a poisson distribution with mean 3. what is the probability of exactly 2 accidents over the course of 2 weeks?
Answers
The probability that there will be exactly 2 accidents during the next
two weeks is 0.9828.
A Poisson distribution in statistics is a probability distribution that is used to demonstrate how frequently an event is expected to happen over a certain period of time. It is a count distribution, to put it another way. In order to comprehend separate events that happen at a steady pace throughout the course of a certain period of time, Poisson distributions are frequently utilized.
Using the Poisson distribution:
2 weeks ⇒ λ = 6.
P( X ≥ 2 ) = 1 – [ P( X = 0 ) + P( X = 1 ) ] = \(1-[\frac{6^{0}*e^{-6} }{0!} + \frac{6^{1}*e^{-6} }{1!}]\)
= 1-[0.0024+0.0148] = 0.9828
To know more about probability visit: brainly.com/question/11234923
#SPJ4
These triangles are similar. I need to know what x is.

Answers
The value of x as per the similarity of triangles is = 7.1.
What is similarity of triangles?If two triangles' sides have the same ratio or proportion and their angles are the same (corresponding angles), then the triangles will resemble one another (corresponding sides).
Similar triangles may have varied side lengths when compared individually, but they must all have the same ratio of their side lengths and equal angles.
Now in the figure, the triangles are similar.
So, sides of the triangles will be proportional to each other.
Now, 9/15 = 4.3/x
⇒ x = (4.3 × 15)/ 9
⇒ x = 7.1
Therefore, the value of x as per the similarity of triangles is = 7.1.
To know more about similarity of triangles, visit:
https://brainly.com/question/14926756
#SPJ1
What is the linear function equation that best fits the data set? 1) y = -2x + 5. 2) y = 2x + 5. 3) y = -1/2x + 5. 4) y = 1/2x - 5.

Answers
Without specific information about the data set, it is not possible to determine which equation is the best fit.
To determine the linear function equation that best fits the data set, we need more information about the data set itself. Without the data points or any other details, we cannot accurately determine which linear function equation is the best fit.
However, I can provide a general explanation of the four options:
y = -2x + 5: This is a linear equation with a negative slope of -2. It represents a line that decreases as x increases. The y-intercept is 5.
y = 2x + 5: This is a linear equation with a positive slope of 2. It represents a line that increases as x increases. The y-intercept is 5.
y = -1/2x + 5: This is a linear equation with a negative slope of -1/2. It represents a line that decreases at a slower rate as x increases. The y-intercept is 5.
y = 1/2x - 5: This is a linear equation with a positive slope of 1/2. It represents a line that increases at a slower rate as x increases. The y-intercept is -5.
Without specific information about the data set, it is not possible to determine which equation is the best fit. The best fit would depend on how well the equation aligns with the actual data points.
for such more question on data set
https://brainly.com/question/27358262
#SPJ8
What is the greatest measure of length? A. 5,000 meters B. 6,000 centimeters C. 30,000 millimeters D. 1 kilometer
Answers
Answer: A. 5,000 meters
Step-by-step explanation:
Starting with the smallest unit which is option C. There are 10 millimeters in one centimetre. Option c in centimeters is:
= 30,000 / 10
= 3,000 meters.
Option c is smaller than B and so is incorrect.
A meter is 100 centimeters. Option b in meters is;
= 6,000 / 100
= 60 meters
This is less than option A so is incorrect.
A kilometer is 1,000 meters so option A in meters is:
= 5,000 / 1,000
= 5 kilometers
This is higher than option d so option A is correct.
solve 8x-7y=18 for y?
Answers
Answer:
y = 8/7x -18/7
Step-by-step explanation:
8x-7y=18
Subtract 8x from each side
8x-8x-7y=-8x+18
-7y = -8x+18
Divide each side by -7
-7y/-7 = ( -8x+18)/-7
y = 8/7x -18/7
You started hiking at 31.3 feet below sea level. At the end of your hike, you were at 56.2 feet above sea level. How many feet did you climb?
Answers
Answer:
24.9
Step-by-step explanation:
56.2-31.3=24.9
Can someone please help me out with this….

Answers
Answer:
Box 1 = 3 Box 2 = -1
Step-by-step explanation:
3 and 1 is the answer correct me if im wrong
HOPE IT HELPS:)
Describe the relationship between <1 and <5

Answers
Angles 1 and 5 constitutes one of the pairs
Step-by-step explanation:
Morty does not try hard at work, because he believes that promotions are completely random and that he has no control over whether he will get promoted. According to expectancy theory, Morty most likely has a(n) ________ locus of control
Answers
Morty most likely has an external locus of control according to expectancy theory, which suggests that he believes outcomes are determined by external factors and not within his control.
Expectancy theory is a psychological framework that examines individuals' motivation and decision-making processes. It posits that people's motivation to exert effort is influenced by three key factors: expectancy, instrumentality, and valence.
Locus of control is an important concept within expectancy theory and refers to individuals' beliefs about the degree to which they have control over the outcomes in their lives.
In Morty's case, his belief that promotions are completely random and beyond his control indicates an external locus of control.
He perceives promotions as being determined by external factors such as luck or favoritism, rather than his own efforts or abilities.
This belief diminishes his motivation to try hard at work because he does not see a direct link between his performance and the desired outcome of promotion.
Individuals with an external locus of control tend to attribute outcomes to external forces, such as luck or fate, rather than their own actions.
They may feel powerless and have lower motivation to actively pursue their goals or exert effort to achieve desired outcomes.
In Morty's case, his perception that promotions are random suggests that he lacks the belief that his efforts will directly influence his chances of promotion, leading to reduced motivation and a lack of effort in his work.
Learn more about Locus of control here:
https://brainly.com/question/27995502
#SPJ11
Suppose that, from measurements in a microscope, you determine that a certain bacterium covers an area of 1. 50μm2. Convert this to square meters.
Answers
Converting 1. 50μm² to square meters gives 1. 5 × 10 ^-11
What is conversion of units?Conversion of units is defined as the conversion of different units of measurement for the same quantity, mostly through multiplicative conversion factors.
From the information given, we are to convert micrometers to square meters
Note that:
1 micrometer ( μm²) = 10^-12m²
Given 1. 50μm² = xm²
cross multiply
x = 1. 50 × 10^-12
x = 1. 50 × 10^-12
x = 1. 50 × 10^-12
x = 1. 5 × 10 ^-11 square meters
Thus, converting 1. 50μm² to square meters gives 1. 5 × 10 ^-11
Learn more about conversion here:
https://brainly.com/question/16851332
#SPJ1
a bag contains 3 red balls and 2 blue balls. you draw a ball at random, then without replacing it, draw another ball. what is the probability that the first ball is red and the second ball is blue?
Answers
The probability of drawing a red ball on the first draw is 3/5. Since the ball is not replaced, there are now 4 balls left in the bag, with 2 blue balls. Thus, the probability of drawing a blue ball on the second draw is 2/4 or 1/2. Therefore, the probability of drawing a red ball on the first draw and a blue ball on the second draw is (3/5) * (1/2) = 3/10.
To calculate the probability of drawing a red ball on the first draw and a blue ball on the second draw, we use the multiplication rule of probability. According to this rule, the probability of two events A and B occurring is the product of the probabilities of each individual event.
Here, event A is drawing a red ball on the first draw, which has a probability of 3/5 since there are 3 red balls out of 5 total balls in the bag. Since the ball is not replaced after the first draw, event B is drawing a blue ball on the second draw from the remaining 4 balls. There are 2 blue balls out of 4 total balls left in the bag, so the probability of drawing a blue ball on the second draw given that a red ball was drawn on the first draw is 2/4 or 1/2.
Thus, the probability of drawing a red ball on the first draw and a blue ball on the second draw is (3/5) * (1/2) = 3/10. Therefore, the probability of drawing a red ball on the first draw and a blue ball on the second draw is 3/10.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
A person places $38100 in an investment account earning an annual rate of 4%, compounded continuously. Using the formula � = � � � � V=Pe rt , where V is the value of the account in t years, P is the principal initially invested, e is the base of a natural logarithm, and r is the rate of interest, determine the amount of money, to the nearest cent, in the account after 9 years.
Answers
The amount of money in the account after 9 years with continuous compounding is $54,652.71.
How do we determine the amount of money?The formula for calculating the future value of an investment with continuous compounding is: A = Pe^(rt) where P = $38100, r = 4% = 0.04 and t = 9 years
Substituting these values into the formula, we get:
\(A = 38100 x e^(0.04 x 9)\\A = 38100 x e^0.36\\\A = 38100 x 1.433329\\A = $54,652.71\)
Read more about continuous compounding
brainly.com/question/30751082
#SPJ1
answer choices:
(16,8)
(2,8)
(-6,8)
(-8,8)

Answers
the value of “y” varies directly with “x”. if y= 56, then x= 4
Answers
PLEASE HELP!!
Which expression is equivalent to (12x^(4))/(4x^(16))

Answers
The number of Votive candles varies directly as the price. What is the ratio of candles to dollars?

Answers
Answer: $2 per candle
Step-by-step explanation:
Dollars to candles
4 to 2
is equivalent to
2 to 1
$2 per candle
The ratio of candles to dollars is 1/2.
$2 per candle.
Option B is the correct answer.
What are coordinates in a graph?The coordinates in a graph indicate the location of a point with respect to the x-axis and y-axis.
The coordinates in a graph show the relationship between the information plotted on the given x-axis and y-axis.
We have,
The following coordinates are from the graph.
(2, 4), (4, 8), (8, 16).
The x-coordinates denote the number of candles.
The y-coordinate denotes the cost.
Now,
(2, 4) means 2 candles cost $4.
(4, 8) means 4 candles cost $8.
(8, 16) means 8 candles cost $16.
The ratio of candles to dollars.
= 2/4
= 1/2
This means,
The cost of one candle is $2.
Thus,
The cost of one candle is $2.
Learn more about coordinates here:
https://brainly.com/question/13118993
#SPJ2
A dairy farmer milks his two cows every day. He determined the chance that he gets anywhere between 12 and 14 gallons of milk in one day is around 32%. Identify the method of probability the farmer used to reach this conclusion. Select the correct answer below: theoretical relative frequency
Answers
The dairy farmer used the relative frequency method of probability to reach his conclusion.
Relative frequency is a method of calculating probability that is based on the observation of how often an event occurs in a sample. The farmer likely observed how often he gets between 12 and 14 gallons of milk in a day and used that data to calculate the probability of it happening.
In contrast, theoretical probability is based on the assumption that all possible outcomes are equally likely. It is calculated by dividing the number of desired outcomes by the total number of possible outcomes.
Therefore, the correct answer is relative frequency.
Know more about relative frequency here:
https://brainly.com/question/29739263
#SPJ11