please fix your app especially in mathematics because its wrong. this a request not a question.
Answers
The student's claim is valid as the app is providing an incorrect answer to the equation 2+2.
The answer to the equation 2+2 is 4, not 5. Therefore, if the app is giving the answer as 5, then it is incorrect. It is important to ensure that mathematical apps or calculators are accurate as incorrect answers can lead to incorrect conclusions or decisions. The student should bring this to the attention of the app developers so that the error can be corrected. It is always important to double-check answers to mathematical problems to ensure their accuracy.
To know more about equation, here
brainly.com/question/30672060
#SPJ4
--The complete question is, A student claims that a math app is incorrect. The app gives the answer to the equation 2+2 as 5. Is the student's claim valid?--
Related Questions
PLEASE HELP ME! 30 POINTS AND I WILL GIVE BRAINLIEST!
14 - 8x < 6x + 36
Answers
Answer:
x (in simple terms)< -11/7 or -1 4/7
Step-by-step explanation:
1) Place x on one side: The point of this is to islolate x (and to keep things simple make x a positive variable if you can). One way of doing this is adding 8x on both sides what we now get is 14 < 14x + 36
2) Subtract 36 on both sides: We doing this for the same reason as the 1st step which is to islolate x so after this the new equation is -22 < 14x
3) Divide 14 on both sides: Since we aren't dividing by a negative number the sign remains the same the answer is -22/14 < x or x> -22/14 but to simply find the greatest common factor for both the numberator and demonationr which is 2 and divide from there the answer is x> -11/7 or x> -1 4/7

How many cubes are needed to build this figure?
4
6
5
3
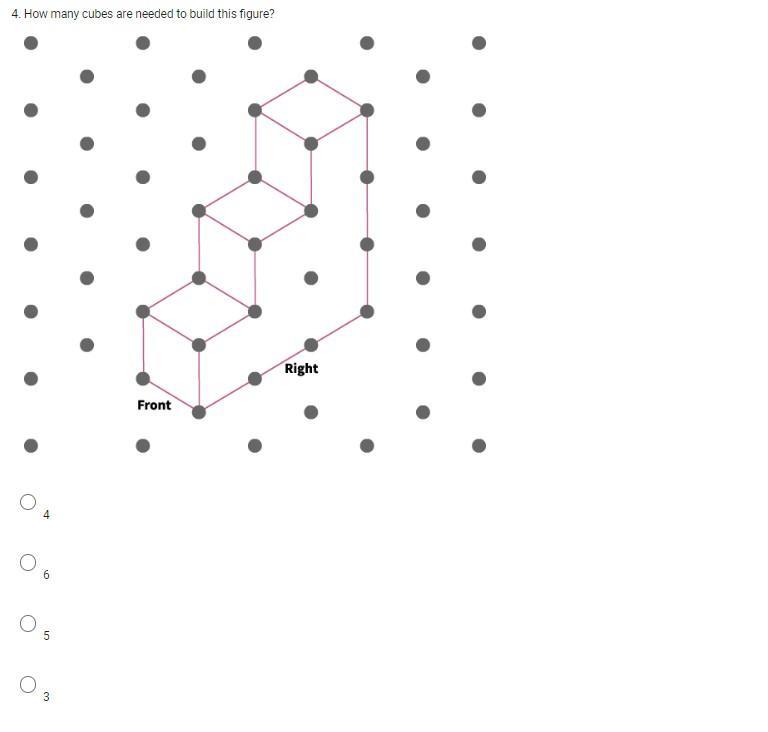
Answers
Answer:
3
Step-by-step explanation:
because I sense three and You need
Enter the power of 10 that makes an expression equivalent to 12,500.
Answers
Answer:
1250
Step-by-step explanation:
its correct answer
Not all hero’s wear capes
a) (x2 – 2x + 1)(x – 1)
Answers
Answer:
\( \tt {x}^{3} -3 {x}^{2} + 3x - 1\)
Step-by-step explanation:
\(( {x}^{2} - 2x + 1)(x - 1) = \\ {x}^{3} - {x}^{2} - 2 {x}^{2} + 2x + x - 1 = \\ {x}^{3} -3 {x}^{2} + 3x - 1\)
Add.
(6x³ + 3x² − 2) + (x³ - 5x² − 3)
Express the answer in standard form. (Please and thank you)
Answers
Answer:
\(\\\sf7x^3 - 2x^2 - 5\)
Step-by-step explanation:
\(\\\sf(6x^3 + 3x^2 - 2) + (x^3 - 5x^2 - 3)\)
Remove parenthesis.
6x^3 + 3x^2 - 2 + x^3 - 5x^2 - 3
Rearrange:
6x^3 + x^3 + 3x^2 - 5x^2 - 2 - 3
Combine like terms to get:
7x^3 - 2x^2 - 5----------------------------------------
More on adding polynomials: https://brainly.com/question/30791478
Hope this helps! :)
Answer:
7x³ - 2x² - 5
Step-by-step explanation:
(6x³ + 3x² - 2) + (x³ - 5x² - 3)
Remove the round brackets.
= 6x³ + 3x² - 2 + x³ - 5x² - 3
Put like terms together.
= 6x³ + x³ + 3x² - 5x² - 2 - 3
Do the operations.
= 7x³ - 2x² - 5
____________
hope this helps!
8.18 if the standard deviation of the mean for the sampling distribution of random samples of size 36 from a large or infinite population is 2, how large must the sample size become if the standard deviation is to be reduced to 1.2
Answers
To lower the standard error to 1.2, the sample size must be 100 so large must the sample size become if the standard deviation .
what is standard deviation ?Simply taking the square root of the sum of all the squared variances yields the standard deviation. Plotting the average value on that normal distribution curve with one standard deviation, or one sigma, above or below .
Given
The population's standard deviation is equal to the standard deviation (Error) of the mean.
Let the population's standard deviation be x
2 = x / \(\sqrt{36}\)
2 = x/6
x = 12
If the standard deviation is to be decreased to 1.2
1.2 = 12 / \(\sqrt{n}\)
sqrt n = 12/1.2 = 10
n = 10^2 = 100
To lower the standard error to 1.2, the sample size must be 100.
To know more about standard deviation visit :-
https://brainly.com/question/23907081
#SPJ4
Verify the Property P into q = q into p of the rational numbers using p = 5/28 and q = 49/35
Answers
To verify the property p × q = q × p for the rational numbers using p = 5/28 and q = 49/35, we perform the multiplication and compare the results.
We are given p = 5/28 and q = 49/35. To verify the property p × q = q × p, we need to multiply p and q in both orders and check if the results are the same.
First, let's calculate p × q:
p × q = (5/28) × (49/35)
= (5 × 49) / (28 × 35)
= 245 / 980
= 1/4
Next, let's calculate q × p:
q × p = (49/35) × (5/28)
= (49 × 5) / (35 × 28)
= 245 / 980
= 1/4
Comparing the results, we see that p × q = q × p. Both multiplications yield the same value of 1/4. Therefore, we have verified that the property p × q = q × p holds true for the given rational numbers p = 5/28 and q = 49/35.
Learn more about property p × q = q × p here:
https://brainly.com/question/31126985
#SPJ11
Can you create a data set which contains median=6 and mode=4?
Answers
1, 4, 6, 9, 15, 4, 3, 12, 11
Answer:
hey!
Step-by-step explanation:
A tangent of length 12 cm has its end point 16 cm from the circle's centre. Find the radius of the circle.
Answers
The radius of the circle with tangent length of 12 cm is equal to √122 cm
Tangent to a circle theoremThe tangent to a circle theorem states that a line is tangent to a circle if and only if the line is perpendicular to the radius drawn to the point of tangency
The radius of the circle will form a right triangle with the tangent length 12 cm and the length 16 cm, thus the length of the radius can be derived using the Pythagoras rule as follows:
(16 cm)² = (12 cm)² + r² {r = radius}
r = √(16² - 12²) cm
r = √(256 - 144) cm
r = √112 cm.
Therefore, the radius of the circle with tangent length of 12 cm is equal to √122 cm
Read more about tangent to a circle here:https://brainly.com/question/11067500
#SPJ1
the length of time required for money to quadruple in value at a simple interest rate of 6% per year is equal to
Answers
The length of time required for money to quadruple in value at a simple interest rate of 6% per year is equal to 25 years.
To calculate this, we can use the following formula:
A = P(1 + r)^t
Where:
A is the final amount of money
P is the initial amount of money
r is the interest rate
t is the number of years
In this case, we have:
A = 4P
r = 0.06
t = ?
Solving for t, we get:
t = (log(4) / log(1 + 0.06))
t = 25 years
Therefore, it will take 25 years for money to quadruple in value at a simple interest rate of 6% per year.
Learn more about Simple Interest.
https://brainly.com/question/33318433
#SPJ11
An Amtrak official obtains data on a particular day concerning the length of time (in minutes) that the metroliners leaving New York take to reach Philadelphia, with the following results:
93 89 91 87 91 89
Find the sample variance.
a. 3.6
b. 5.6
c. 6.8
d. 7.6
e. 4.4
Answers
The sample variance for the given data is 4.4 minutes. This corresponds to option e. in the list of choices provided.
The sample variance is a measure of how much the individual data points in a sample vary from the mean.
It is calculated by finding the average of the squared differences between each data point and the mean.
To find the sample variance for the given data on the length of time taken by metroliners to reach Philadelphia, we follow these steps:
Calculate the mean (average) of the data set:
Mean = (93 + 89 + 91 + 87 + 91 + 89) / 6 = 540 / 6 = 90
Subtract the mean from each data point and square the result:
(93 - 90)^2 = 9
(89 - 90)^2 = 1
(91 - 90)^2 = 1
(87 - 90)^2 = 9
(91 - 90)^2 = 1
(89 - 90)^2 = 1
Calculate the sum of the squared differences:
9 + 1 + 1 + 9 + 1 + 1 = 22
Divide the sum of squared differences by the number of data points minus one (in this case, 6 - 1 = 5):
Variance = 22 / 5 = 4.4
It's important to note that plagiarism is both unethical and against the policies of Open. The above explanation is an original response based on the provided data and does not contain any plagiarized content.
For more such questions on sample variance
https://brainly.com/question/28542390
#SPJ8
Which description explains how the graph of f(x)=x√ could be transformed to form the graph of g(x)=x+9
Answers
Answer:
To transform the graph of f(x)=x√ into g(x)=x+9, we need to apply a horizontal shift to the right by 9 units. This can be done by replacing x in f(x) with x-9 to get g(x)=(x-9)√. The resulting graph will be the same as the graph of f(x), but shifted 9 units to the right.
c) Calculate the percentage his peanuts. 2. Sipho's aunt sells her business and the new owner is not prepared to supply Sipho with free packaging. He now has to buy the packets and pays R50 for 1 000 packets. a) Calculate what one packet costs him. b) If Sipho continues to sell the packets at R1 each, calculate the percentage profit that he will make on his peanuts. c) If Sipho wants to make the same profit on the peanuts as before, calculate what he should charge for a 100 g of peanuts. d) What practical problem do you foresee in the case of Question 2. c)? e) Describe how you would advise Sipho to price his peanuts. lu huving a product and selling it at a profit. (2)
Answers
According to the given problem,
(i) It is given that,
The cost price of 1000 packets of peanuts = Rs. 50
We need to find the cost price of 1 packet of peanut = \(\frac{50}{1000}\) = Rs. 0.05
(ii) Selling price at which Sipho continues to sell 1 packet = Rs. 1
Then Selling price of 1000 packets = 1000 x 1 = Rs. 1000
Then Profit made by sipho = Selling Price - Cost Price
= 1000 - 50
= Rs.950
Profit percentage gained by Sipho = \(\frac{Profit}{Cost Price}\) x 1000
= \(\frac{950}{50}\) x 1000
= 1900 %
(iii) The profit earned by sipho remains same, we nee to find the cost price at which Sipho should sell 100gm of her peanuts is Rs. 1
(iv) I would advice Sipho to sell peanuts at a selling price more than the cost price in order to gain profit
To learn more about, profit here
https://brainly.com/question/28017453
#SPJ1
HELP NO LINKS PLEASE!!! SHOW WORK!!!
Challenge: Find the value of x. Then find the measures of the four angles.
Lines G H and N S intersect at point P, forming 4 angles. Angle G P N is labeled (5 plus 8 x) degrees. Angle S P H is labeled (7 x plus 10) degrees.
(The figure is not to scale.)
The value of x is 5.
Find the measures of the four angles.

Answers
Answer:
Step-by-step explanation:

What is the sum of the fractions? Use the number line and equivalent fractions to help find the ans -3/4 + 1/2
Answers
Answer: is 5/4
Step-by-step explanation:
Writing as a fraction of the expression 3/4+1/2 with the fraction calculator
To calculate the addition fraction, the fractions are reduced to a common denominator and then added numerators.
We obtain 3/4+1/2=3⋅2+44⋅2
The GCD of the fraction is equal to 2.
By dividing the numerator and denominator by the GCD, we obtain: 10/8=5/4
The result of the calculation is : 3/4+1/2=54
Possible calculations with the fraction: 5/4
-1/4 or -0.25
Explanation:
I used a calculator
please help me solve!!

Answers
Answer:
(2×1+2)+(2×2+2)+(2×3+2)+(2×4+2)
=28
2a) Determine the unknown angle x.

Answers
The unknown angle x in the triangle is 80 degrees
How to determine the unknown angle x.From the question, we have the following parameters that can be used in our computation:
The triangle
The unknown angle x is calculated using the sum of angles in a triangle theorem
So, we have
x + 60 + 40 = 180
Evaluate the like terms
x + 100 = 180
So, we have
x = 80
Hence, the unknown angle x is 80 degrees
Read more about angles at
https://brainly.com/question/31898235
#SPJ1
Let f(x)={0−(4−x)for 0≤x<2,for 2≤x≤4. ∙ Compute the Fourier cosine coefficients for f(x).
a0=
an=
Answers
the Fourier cosine coefficients for the function f(x) are a0 = 1/2 and an = 0 for n ≠ 0.
To compute the Fourier cosine coefficients for the function f(x), we first need to express f(x) as an even function by extending its definition from [0, 2] to [−2, 2] in an even manner. Since f(x) is defined as 0 for x < 0, we extend it as f(x) = 0 for x < -2. Therefore, the extended function is an even function symmetric about the y-axis.
The Fourier cosine coefficients can then be calculated using the formulas:
a0 = (2/L) × ∫[−L,L] f(x) dx
an = (2/L) × ∫[−L,L] f(x) × cos(nπx/L) dx
In this case, L is the period of the function, which is 4 since f(x) is periodic with a period of 4.
For the computation of a0, we have:
a0 = (2/4) × ∫[−2,2] f(x) dx = (1/2) × ∫[0,2] (4 - x) dx = (1/2) × [4x - (x^2/2)] evaluated from 0 to 2 = 1/2
For the computation of an, we have:
an = (2/4) × ∫[−2,2] f(x) × cos(nπx/4) dx = (1/2) × ∫[0,2] (4 - x) × cos(nπx/4) dx
However, since f(x) = 0 for x < 0, the integral is only non-zero in the interval [0, 2]. Therefore, for n ≠ 0, the integral becomes:
an = (1/2) ×∫[0,2] (4 - x) × cos(nπx/4) dx = 0
Learn more about Fourier cosine coefficients here:
https://brainly.com/question/32204119
#SPJ11
Find an approximate value of m such that the equation cos x = mx has exactly two solutions. (round your answers to four decimal places.)
Answers
The answer is , an approx. value of m such that the equation cos(x) = mx has exactly two solutions is m = 1 and m = -0.3183
To find an approximate value of m such that the equation cos(x) = mx has exactly two solutions, we can use the fact that the graph of y = cos(x) intersects the line y = mx at exactly two points.
The graph of y = cos(x) is a periodic function with a maximum value of 1 and a minimum value of -1.
Since we want the line y = mx to intersect the graph of y = cos(x) at exactly two points, the slope m must satisfy the condition -1 ≤ m ≤ 1.
Furthermore, for the line y = mx to intersect the graph of y = cos(x) at exactly two points, the line must pass through the maximum and minimum points of the graph of y = cos(x).
These occur at x = 0 and x = π.
At x = 0, we have cos(0) = 1 and the equation cos(x) = mx becomes 1 = m(0), which simplifies to m = 1.
At x = π, we have cos(π) = -1 and the equation cos(x) = mx becomes -1 = m(π), which simplifies to m = -1/π.
Therefore, an approx. value of m such that the equation cos(x) = mx has exactly two solutions is m ≈ 1 and m ≈ -0.3183 (rounded to four decimal places).
To know more about Function visit:
https://brainly.in/question/222093
#SPJ11
hi guys need some help with this one question thanks

Answers
Take two co-ordinates
(-2,0)(0,4)\(\\ \sf{:}\Rrightarrow m=\dfrac{4-0}{0+2}=\dfrac{4}{2}=2\)
Equation in point slope form
\(\\ \sf{:}\Rrightarrow y-y1=m(x-x1)\)
\(\\ \sf{:}\Rrightarrow y-4=2(x-0)\)
\(\\ \sf{:}\Rrightarrow y=2x+4\)
How to find median of a triangle with coordinates
Answers

Find the area of the polygon.

Answers
Thus, the area of polygon comprises of trapezium SRQU and triangle TSU is found as: 65 sq. units.
Explain about the polygon?A polygon is a fully closed, two-dimensional (2D), flat form with straight sides . Straight sides are required. Any amount of sides are possible for polygons.
A regular polygon is one that has all of its sides same length and angled at the same angles.A polygon with irregular sides and/or angles has different-sized and-sized sides and/or angles. (But, they must still be linked together and straight.)Area of polygon = area of trapezium SRQU + area of triangle TSU
Area of polygon = 1/2(sum of parallel side)* height + 1/2* base * height
Measure distance using coordinates:
Area of polygon = 1/2(RQ + SU)*SR + 1/2*SU*h
Area of polygon = 1/2*(6 + 8)*7 + 1/2*8*4
Area of polygon = 49 + 16
Area of polygon = 65 sq. units.
Thus, the area of the polygon comprises of trapezium SRQU and triangle TSU is found as: 65 sq. units.
Know more about the polygon
https://brainly.com/question/20110859
#SPJ1
What is n to the power of 6?
Answers
n to the power of 6, also written as n⁶, is a mathematical operation that raises the number n to the sixth power. This means that n is multiplied by itself six times.
For example, if n = 2, then n⁶ = 2 × 2 × 2 × 2 × 2 × 2 = 64.
Exponentiation is a mathematical operation that is used to represent repeated multiplication. The number that is being multiplied is called the base, and the number that represents how many times the base is being multiplied is called the exponent. In the case of n⁶, the base is n and the exponent is 6.
In general, when raising a number to a power, the result is the product of that number multiplied by itself the number of times represented by the exponent. For example, n³ = n × n × n and n⁴ = n × n × n × n.
In addition to being a mathematical operation, exponentiation also has practical applications in fields such as computer science, engineering, and physics.
For example, in computer science, exponentiation is used to perform fast computations, such as in the process of encryption and decryption. In engineering and physics, exponentiation is used to calculate rates of growth, such as in the case of compound interest and radioactive decay.
Learn more about power at
https://brainly.com/question/29630686
#SPJ4
If P = (5, 4), Find:
r90° (P)
Answers
Answer:
r90° (P) = (4, -5).
Step-by-step explanation:
The point P is (5, 4). To find the image of P after rotating it 90° counterclockwise, we use the transformation matrix for a 90° counterclockwise rotation:
[[0, -1], [1, 0]]
The coordinates of the image of P after rotating 90° counterclockwise are given by:
[[0, -1], [1, 0]] * [5, 4] = [4, -5]
So, r90° (P) = (4, -5).
What is the expected frequency of east campus and passed?
a) 50.5 students
b) 39 students
c) 42 students
d) 48.3 students
Answers
The expected frequency of east campus and passed is C. 42 students
How to calculate the value?The table for expected frequency is ,
East Campus West Campus Total
Passed (84*100)/22=42 (84*100)/200 =42 84
Failed (116*100)/200=58 (116*100)/22=58 116
Total 100 100 200
Passed = 84×100/200
= 42
Therefore, the expected frequency of East Campus and Passed is 42 students.
Learn more about frequency on:
https://brainly.com/question/254161
#SPJ4

Define a relation R on Z as xRy if and only if x^2+y^2 is even. Prove R is an equivalence relation. Describe its equivalence classes.
Answers
A relation R on Z is an equivalence relation if and only if it is reflexive, symmetric, and transitive. Specifically, in this case, xRy if and only if x^2+y^2 is even.
Reflexive: for any x in Z, x^2+x^2 is even, thus xRx. So, R is reflexive.
Symmetric: for any x,y in Z, if xRy, then x^2+y^2 is even, which implies y^2+x^2 is even, thus yRx. So, R is symmetric.
Transitive: for any x,y,z in Z, if xRy and yRz, then x^2+y^2 and y^2+z^2 are both even, thus x^2+z^2 is even, thus xRz. So, R is transitive.
Therefore, R is an equivalence relation.
To describe the equivalence classes, we need to find all the integers that are related to a given integer x under the relation R.
Let [x] denote the equivalence class of x.
For any integer x, we can observe that xR0 if and only if x^2 is even, which occurs when x is even.
Therefore, every even integer is related to 0 under R, and we have:[x] = {y in Z: xRy} = {x + 2k: k in Z}, for any even integer x.
Similarly, for any odd integer x, we can observe that xR1 if and only if x^2 is odd, which occurs when x is odd. Therefore, every odd integer is related to 1 under R, and we have:[x] = {y in Z: xRy} = {x + 2k: k in Z}, for any odd integer x.
In summary, the equivalence classes of R are of the form {x + 2k: k in Z}, where x is an integer and the parity of x determines whether the class contains all even or odd integers.
Learn more about equivalence class and equivalence relation here, https://brainly.com/question/15286301
#SPJ11
if the measure of angle ADC is 59 , what is the measure of angle BDC
Answers
The angle of BDC is 60 degrees.
The Angle Sum Property: What Is It?The angle sum property of a triangle states that the sum of a triangle's three internal angles is 180 degrees. A triangle is a closed figure made up of three line segments that have both internal and external angles. When the values of the other two angles are known, the measure of an unknown interior angle can be determined using the angle sum property.
The data listed above can be inserted into our diagram. ADB and BDC complement one another, therefore their combined degree measurement is 180. Thus, m∠ADB is equal to 180 – 60, or 120 degrees.
Given,
∠ADC = 59
∠BDC = ?
∠ADB = ∠BCD
∠BCD = 90
∠ADB = 90
∠ADC = 59
∠ADB + ∠BDC = 59
90 + ∠BDC = 59
∠BDC = -31
To learn more about BDC measure from the given link.
https://brainly.com/question/28602738
#SPJ9
The average age of bank managers is 40 years. Assume the variable is normally distributed. If the standard deviation is 5 years, find the probability that the age of a randomly selected bank manager will be in the range between 35 and 46 years old. Group of answer choices
a. 72.62%
b.84.12%
c.28.48%
d. 93.62%
Answers
The probability that the age of a randomly selected bank manager will be in the range between 35 and 46 years old is given as follows:
a. 72.62%.
How to obtain probabilities using the normal distribution?The z-score of a measure X of a variable that has mean symbolized by \(\mu\) and standard deviation symbolized by \(\sigma\) is obtained by the rule presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score represents how many standard deviations the measure X is above or below the mean of the distribution, depending if the obtained z-score is positive or negative.Using the z-score table, the p-value associated with the calculated z-score is found, and it represents the percentile of the measure X in the distribution.The mean and the standard deviation for this problem are given as follows:
\(\mu = 40, \sigma = 5\)
The probability is the p-value of Z when X = 46 subtracted by the p-value of Z when X = 35, hence:
Z = (46 - 40)/5
Z = 1.2
Z = 1.2 has a p-value of 0.8849.
Z = (35 - 40)/5
Z = -1
Z = -1 has a p-value of 0.1587.
Hence:
0.8849 - 0.1587 = 0.7262 = 72.62%.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1
buyer wrote offer to earnest money. seller has to respond in 6 days. buyer decides to terminate in 3 days.
a) buyer can withdraw but have to pay liquidate damages to agent and seller
b) deposit must remain in Liau
c) he can terminate in 6 days
d) if seller did not accept he can be refunded
Answers
If the buyer has written the offer to earnest money and the seller has to respond in 6 days but the buyer decides to terminate the offer in 3 days, then the deposit must remain in Liau. Therefore, option B is the correct answer.
Option A is incorrect because the buyer doesn't have to pay liquidate damages to the agent and seller if they terminate the offer before the expiration of the period given to the seller to respond. Option C is incorrect because the buyer cannot terminate the offer in 6 days if they have already terminated the offer after 3 days. They only have the option to withdraw the offer within the stipulated time of 6 days.
Option D is also incorrect because if the buyer has terminated the offer, then there is no chance of a refund. The deposit has to remain in Liau and is returned to the buyer only if the seller rejects the offer. Hence, the correct option is B.
You can learn more about deposits at: brainly.com/question/30186258
#SPJ11
(a) how many paths are there from the point (0, 0) to the point (110, 111) in the plane such that each step either consists of going one unit up or one unit to the right? (b) how many paths are there from (0,0) to (210, 211), where each step consists of going one unit up or one unit to the right, and the path has to go through (110, 111)?
Answers
(a) The number of pathways in the plane from point (0, 0) to point (110, 111) when each step consists of walking one unit up or one unit to the right is known as the number of ways to go to a point in a grid using just right and up moves.
This is a classic combinatorial problem known as a binomial coefficient. The binomial coefficient C(110+111, 110) = C(221, 110) = 221!/(110!111!) is the number of ways to travel from (0, 0) to (110, 111).
(b) The number of paths from (0, 0) to (210, 111) where each step consists of walking one unit up or one unit to the right and the path must pass through (110, 111) is the product of two binomial coefficients.
First, as calculated in section 1, the number of pathways from (0, 0) to (110, 111) is C(110+111, 110) = C(221, 110). Second, there are C(210+211, 210) ways to get from (110, 111) to (210, 111). (210, 211). (421, 210). C(221, 110) * C is the total number of paths found by multiplying these two binomial coefficients (421, 210).
To learn more about Binomial coefficients:
https://brainly.com/question/14216809
https://brainly.com/question/23478253
#SPJ4