please help and explain with words please
find the roots of the polynomial
8t^2-2t-3
Answers
Answer:
For a polynomial of the form ax²+bx+c, rewrite the middle term as a sum of two terms whose product is a⋅c = 8⋅ −3=−24 and whose sum is b=−2.
8t²+4t−6t−3
Factor out the greatest common factor from each group.
4t(2t+1)−3(2t+1)
Factor the polynomial by factoring out the greatest common factor, 2t+1.
(2t+1)(4t−3)
Step-by-step explanation:
Related Questions
How much tax will be applied to an order for cupcakes that costs $12.75 if the tax rate is 4%?
Answers
Answer:
$13.26
Step-by-step explanation:
12.75 × 0.04 = 0.51
0.51 + 12.75 = 13.26
Answer:
$12.75 cupcakes
Multiply the $12.75 x .04 = .51
$12.75 + .51 = $13.26 total
Step-by-step explanation:
5. A bottle contains 2 liters of juice. How many milliliters of juice is that?
Answers
Answer:
The answer would be 2000
Step-by-step explanation:
Knowing that there are 1000 milliliters in 1 liter, you can multiply that by 2 to get 2000. I hope this helps! :)
Object A has a mass of 12 g and a volume of 8 cm3. Object B has a mass of 20 g and a volume of 8 cm3. Which object has a greater density and by how much?
Object A, by 1 gram per cubic centimeter
Object A, by 8 grams per cubic centimeter
Object B, by 1 gram per cubic centimeter
Object B, by 8 grams per cubic centimeter
Answers
Answer:
Obj B, by 1 g/cm^3
Step-by-step explanation:
Obj A = 12g / 8cm^3 = 3g / 2cm^3 = 1.5 g/cm^3
Obj B = 20g / 8cm^3 = 5g / 2cm^3 = 2.5 g/cm^3
2.5 - 1.5 = 1 g/cm^3
Answer:
C. Object B, by 1 gram per cubic centimeter.
Step-by-step explanation:
Density = \(\frac{Mass}{Volume}\)
Volume x Density = \(\frac{Mass}{Volume}\) x Volume (cross both of volumes out)
Volume x Density = Mass
So, what you would do is divide the Mass and Volume, and the density would be the outcome.
Since we see it has a mass of 12g and a volume of \(8 cm^{3}\)
We would then do \(\frac{12 g}{8cm^{3}}\), this gives us 1.5, and \(\frac{20g}{8cm^{3}}\) gives us 2.5, so that would give us the answer C.
Sound travels approximately 335 meters per second. The speed of sound through steel is about 5030 meters per second. When Jackson presses his ear against a steel beam, he hears a high-pitched ring six seconds before hearing the same ring through the air. How far away is the source of that ringing?
Answers
Answer:
2153 meters
Step-by-step explanation:
You want to know the distance to a source of sound if it is heard through a medium with a speed of sound of 5030 m/s 6 seconds before it is heard through a medium with a speed of sound of 335 m/s.
TimeThe relation between time, speed, and distance is ...
time = distance/speed
For some distance d in meters, the two times are d/335 seconds and d/5030 seconds. The time difference is 6 seconds, so we have ...
d/335 -d/5030 = 6
Multiplying by 337010, we have ...
1006d -67d = 2022060
939d = 2022060 . . . . . simplify
d ≈ 2153.42 . . . . . meters
The source of sound is about 2153 meters away.
__
Additional comment
The distance might rightly be rounded to 2150 meters, since the given numbers are 3 significant figures each.
(a) From the 12 albums released by a musician, the recording company wishes to release9 in a boxed set. How many different boxed sets are possible?
(b) There14 are European cities that Rashid would eventually like to visit3. On his next vacation, though, he only has time to visit of the cities: one on Monday, one on Tuesday, and one on Wednesday. He is now trying to make a schedule of which city he'll visit on which day. How many different schedules are possible? (Assume that he will not visit a city more than once.)
Answers
Answer:
ejekkeifjejejrjjdjejejeiriririrj
If Paula divides her pencils among three friends and herself, everyone gets the same number of pencils. If Paula divides her pencils among
five friends and herself, everyone will get the same number of pencils.
How many pencils could Paula have?
A 28
B. 30
C. 42
D. 48
Answers
Simplify square root of 144x^12y^20
Answers
\(~~~\sqrt{144 x^{12} y^{20}}\\\\=\left(144 x^{12} y^{20} \right)^{\tfrac 12}~~~~~~~~~~~~~~~~~~~~~~~;\left[\sqrt a = a^{\tfrac 12 } \right]\\\\=\left(144 \right)^{\tfrac 12} \cdot \left(x^{12 \right)^{\tfrac 12} \cdot \left(y^{20} \right)^{\tfrac 12}\\\\=\left(12^2 \right)^{\tfrac 12} \cdot x^{\tfrac{12}2} \cdot y^{\tfrac{20}2}\\\\=12 x^6y^{10}\)
Answer:
12x⁶y¹⁰
Step-by-step explanation:
√144x¹²y²⁰
--------------------
12 × 12 = 144
-----------------------------------------
12√x¹²y²⁰
-----------------
xx
xx
xx
xx
xx
xx
six sets of two equals x⁶
-----------------------------------
12x⁶√y²⁰
yy
yy
yy
yy
yy
yy
yy
yy
yy
yy
ten sets of two equals y¹⁰
12x⁶y¹⁰
I hope this helps!
Please help ASAP
Thanks

Answers
Answer:
5.3
Step-by-step explanation:
a^2+b^2=c^2
a^2+36=48
subtract 36 from each side
a^2=28
square root; a=5.5~
what is the least common factor for 1,000 and 150
Answers
Answer:
least common multiple: 1000
greatest common factor is 50
least common factor would be 1, but that isn't really a common thing to calculate
Step-by-step explanation:
A school club visits a science museum. Student tickets cost $10 each.
Non-student tickets cost $15 each. The club paid $300 for the tickets.
Which equation below could model this situation? *
A. Y=300(15+10)
B. 300=10x + 15y
C. 25x=300
D. Y=300+10x
Answers
Which equation is equivalent to -y + 2y - 9 = 1 ? y=8
Answers
An ABS (Australian Bureau of Statistics) employee wishes to test the speed (in minutes) with which different online survey designs can be completed. Three different online survey designs have been proposed. One complication in assessing the surveys is the notion that individual differences might influence the speed with which the online forms are completed. To account for individual differences an experiment is arranged so that a survey from each design is completed by each individual. The following results are extracted from a randomised block experiment with three treatment levels (i.e. three types of online survey designs) and five blocks (i.e. 5 individuals). SSBL (sum of squares between blocks) = 3738, SSB (sum of squares between groups) = 1048.93 and SST (sum of squares total) = 5391.33. Based on this information, what is the critical value used to test if there is evidence of an effect due to blocks at the 5% level of significance? Use our textbook statistical table to answer the question.
Answers
The critical value used to test if there is evidence of an effect due to blocks at the 5% level of significance is 10.76.
The critical value can be determined using a statistical table.
The degrees of freedom for the blocks is 4 (df_b = 5 - 1 = 4) and for the treatments is 2 (df_t = 3 - 1 = 2).
The critical value for a 5% level of significance is 10.76.
This value can be found in the statistical table given in the textbook.
The critical value used to test if there is evidence of an effect due to blocks at the 5% level of significance can be calculated by using the F-test statistic.
The F-test is used to compare the variance between the blocks (SSBL) and the variance between the groups (SSB).
The F statistic is calculated by dividing the variance between the blocks (SSBL) by the variance between the groups (SSB).
In this case,
The F statistic is 3738/1048.93 = 3.56.
The critical value for a 5% level of significance can be found using a statistical table.
According to the table,
The critical value for an F statistic of 3.56 with four degrees of freedom in the numerator and four degrees of freedom in the denominator is 10.76
For similar question on critical value:
https://brainly.com/question/30168469
#SPJ11
what is coefficient?
Answers
Answer:
a numerical or constant quantity placed before and multiplying the variable in an algebraic expression (e.g. 4 in 4x y).
Answer:
A coefficient is a numerical or constant quantity placed before and multiplying variable.
Step-by-step explanation:
For example, 4x+8=12. 4 is the coefficient.
Simplify -2 over 3 as a fraction -7 over 4 as a fraction
Answers
Answer:
-2/3 stays the same and -7/4 goes to -1 3/4
Step-by-step explanation:
Answer: -29/12
= -2.41667
12
Step-by-step explanation:
solve the equation
pic:

Answers
The solution to the equation \((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2\) is 10.3891
How to solve the equationFrom the question, we have the following parameters that can be used in our computation:
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2\)
Using the following trigonometry ratio
sin²(x) + cos²(x) = 1
We have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = (\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + 1 + e^2\)
The sum to infinity of a geometric series is
S = a/(1 - r)
So, we have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = \frac{1/2}{1 - 1/2} + \frac{9/10}{1 - 1/10} + 1 + e^2\)
So, we have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 1 + 1 + 1 + e^2\)
Evaluate the sum
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 3 + e^2\)
This gives
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 10.3891\)
Hence, the solution to the equation is 10.3891
Read more about summation notation at
brainly.com/question/15973233
#SPJ1
In the figure, m_2 = 75. Find the measures of the
remaining angles.
PA
Х
1/2
4/3
-m
5/6
8/7
-N
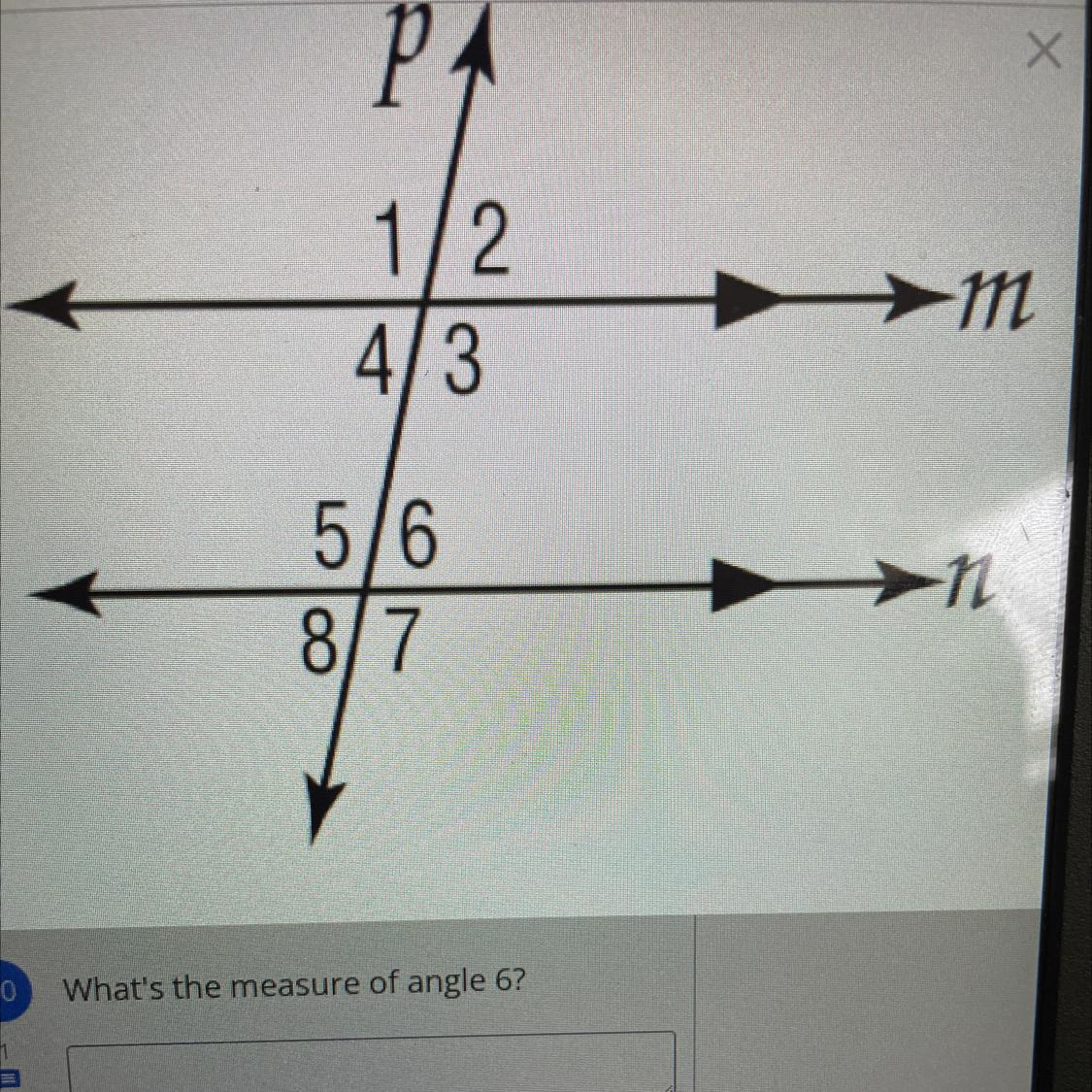
Answers
Answer:
Step-by-step explanation:
If angle 2 is 75, the other angles that are also 75 are angles 4 (it's vertical to angle 2), angle 6 (it's corresponding to angle 2), angle 8 (it's alternate exterior to angle 2). All the other angles measure 180 - 75 which is 105.
Assume that the function f is a one-to-one function. (a) If f(9) = 5, find f-'(5). Your answer is (b)lf f '(- 6) = – 3, find f( – 3).
Answers
The function f is a one-to-one function,
a. \(f^{-1}\)(5) = 9.
b. f(–3) = -18.
(a) Since f(9) = 5, we know that \(f^{-1}\)(5) = 9. Therefore, \(f^{-1}\)(5) = 9.
(b) Since f '(-6) = -3, we can use the definition of the derivative to write:
f '(x) = lim h->0 [f(x + h) - f(x)]/h
Plugging in x = -6 and f '(-6) = -3, we get:
-3 = lim h->0 [f(-6 + h) - f(-6)]/h
Multiplying both sides by h and rearranging, we get:
f(-6 + h) - f(-6) = -3h
Adding f(-6) to both sides, we get:
f(-6 + h) = f(-6) - 3h
Now, we can plug in h = 9 to find:
f(-6 + 9) = f(3) = f(-6) - 3(9) = f(-6) - 27
We don't have enough information to find f(-6) directly, but we do know that f is one-to-one, which means that it has an inverse function. So we can find \(f^{-1}\)(-6) and use it to find f(-6). To do this, we use the fact that:
f(\(f^{-1}\)(x)) = x
Plugging in x = -6, we get:
f(\(f^{-1}\)(-6)) = -6
Since \(f^{-1}\) undoes the action of f, we can also write this as:
\(f^{-1}\)(f(\(f^{-1}\)(-6))) = \(f^{-1}\)(-6)
Using the fact that f(\(f^{-1}\)(x)) = x again, we get:
\(f^{-1}\)(-6) = \(f^{-1}\)(f(\(f^{-1}\)(-6)))
Since f is one-to-one, its inverse function \(f^{-1}\) is also one-to-one, which means that \(f^{-1}\)(f(x)) = x. Therefore, we can simplify the expression above to get:
\(f^{-1}\)(-6) = \(f^{-1}\)(f(\(f^{-1}\)(-6))) = \(f^{-1}\)(-6)
This tells us that \(f^{-1}\)(-6) is equal to itself, which means that \(f^{-1}\)(-6) is -6.
Finally, we can use \(f^{-1}\)(-6) = -6 to find f(-6) using the fact that f(\(f^{-1}\)(x)) = x:
f(-6) = f(\(f^{-1}\)(-6)) = f(-6) = -6 - 3 = -9
Therefore, f(-3) = f(-6 + 3) = f(-6) + 3(-3) = -9 - 9 = -18.
Learn more about the one-to-one function at
https://brainly.com/question/29256659
#SPJ4
The question is -
Assume that the function f is a one-to-one function. (a) If f(9) = 5, find f-'(5). Your answer is (b), lf f '(- 6) = – 3, find f( – 3).
Micro economics, I will give brainliest if you get this correct
Answers
Microeconomics is a branch of economics that focuses on the behavior of individuals and firms in making decisions regarding the allocation of limited resources
Microeconomics is a branch of economics that studies the behavior of individuals and firms in making decisions about the allocation of limited resources, specifically focusing on the interaction of supply and demand in specific markets and how different factors influence the behavior of individuals and firms. It is concerned with the study of how people and firms make decisions about production, consumption, and distribution of goods and services.
Microeconomics analyzes how supply and demand in specific markets interact to determine the prices of goods and services. It also examines how different factors, such as taxes, government regulations, and technological changes, affect the behavior of individuals and firms.
Learn more about Microeconomics here
brainly.com/question/1689139
#SPJ4
Prove Theorem 5.25, Part (5): A x (B-C) = (A × B)-(A × C).
Answers
(A x B) - (A x C) is perpendicular to A and lies in the same plane as A, B, and C., Hence we prove the theorem.
How we can prove the Theorem?We start by expanding the left-hand side of the equation, using the distributive property of multiplication over subtraction:
A x (B-C) = A x B - A x CThis equation is now in the form we want to prove, so we just need to show that it is true. To do this, we can use the distributive property of cross product over subtraction. Recall that the cross product of two vectors A and B is given by:
A x B = |A||B|sinθnwhere |A| and |B| are the magnitudes of the vectors, θ is the angle between them, and n is a unit vector perpendicular to both A and B (according to the right-hand rule).
Using this formula, we can write:
(A x B) - (A x C) = |A||B|sinθn - |A||C|sinϕnwhere ϕ is the angle between A and C. We can factor out |A| and n from this expression:
|A|( |B|sinθn - |C|sinϕn )Now, we need to show that this expression is equal to A x (B-C), which we can do by showing that the magnitudes and directions are the same. Let's start with the magnitudes:
|A x (B-C)| = |A||B-C|sinαwhere α is the angle between A and B-C. Using the distributive property of vector subtraction, we can write:
B - C = B + (-C)and since the magnitude of the negative of a vector is the same as the magnitude of the original vector, we have:
|B - C| = |B + (-C)| = |B| + |-C| = |B| + |C|Substituting this into the previous equation, we get:
|A x (B-C)| = |A||B + (-C)|sinα = |A||B|sinα + |A||C|sinαNow, let's look at the directions. Recall that the direction of the cross product is perpendicular to both vectors being crossed, according to the right-hand rule. The direction of A x B is perpendicular to both A and B, and the direction of A x C is perpendicular to both A and C.
Since B-C is a linear combination of B and C, its direction is somewhere in between the directions of B and C. Specifically, it is perpendicular to A and lies in the plane defined by A, B, and C. Therefore, the direction of A x (B-C) is also perpendicular to A and lies in the same plane as A, B, and C.
Putting it all together, we have shown that:
|A x (B-C)| = |A||B|sinα + |A||C|sinαA x (B-C) is perpendicular to A and lies in the same plane as A, B, and C.This is exactly what we need to show in order to prove the theorem, since the right-hand side of the equation we are trying to prove also has the same magnitude and direction:
|(A x B) - (A x C)| = |A||B|sinθn - |A||C|sinϕnLearn more about Theorem
brainly.com/question/30066983
#SPJ11
On a number line, graph all the temperature that are warmer than -2 degrees Celsius
Answers
(a) A temperature of -2 °C is warmer than a temperature of -5 °C as the temperature on the graph decreases.
(b)The inequality -2>-5 will be used to illustrate the connection between -2 and -5.
What is a graph?A diagram depicting the relationship between two or more variables, each measured along with one of a pair of axes at right angles.
On a number line, graph all the temperature that are warmer than -2°C.
(a)-2 °C temperature is warmer,As the temperature in the graph is decreasing,-2 °C temperature is warmer than -5 °C.
The inequality to express the relationship between -2 and -5 will be -2>-5.
Hence,temperature of -2 °C is warmer than a temperature of -5 °C as the temperature on the graph decreases.
To learn more about the graph, refer to the link;
https://brainly.com/question/14375099
#SPJ2
What are the coefficient terms and Constants of 10x + 5 + 3x + 1
Answers
Answer:
The Coefficients in this expression are 10 and 3, while the constants are 5 and 1.
Step-by-step explanation:
Coefficients = The number that is in front of the variable.
Constant = Any number without a variable.
(Variables are the letters that you may find in an equation or function.)
Hope this helps you :)
Answer:
The coefficient are 10 and 3
The constants are 5 and 1
Step-by-step explanation:
A coefficient is the number in front of any known term.
A constant is a number by itself.
So the coefficient are 10 and 3
The constants are 5 and 1
Which expression is equal to
-18b^-4
Answers
Answer:
\( - \frac{18}{ {b}^{4} } \)
Step-by-step explanation:
\( - 18b {}^{ - 4} \)
express b^-4 with a positive exponent using:
\(a {}^{ - n} = \frac{1}{ {a}^{n} } \)
\( - 18 \frac{1}{ {b}^{4} } \)
\( - \frac{18}{ {b}^{4} } \)
Tell whether the two quantities vary directly. Explain your reasoning.
the number of correct answers on a test and the score on the test
Choose the correct answer below.
OA. No, they do not vary directly. When one quantity increases, the other quantity does not increase.
OB. No, they do not vary directly. When one quantity increases, the other quantity also increases.
C. Yes, they vary directly. When one quantity increases, the other quantity also increases.
OD. Yes, they vary directly. When one quantity increases, the other quantity does not increase.
Answers
The correct statement regarding the variation of the two measures is given as follows:
C. Yes, they vary directly. When one quantity increases, the other quantity also increases.
What are positive and negative association?Two variables have a positive association when the values of one variable increase as the values of the other variable increase, that is, the quantities vary directly.Two variables have a negative association when the values of one variable decrease as the values of the other variable increase, that is, the quantities vary inversely.For this problem, we have that when the number of correct answers on the test increases, the score also does, hence the two quantities vary directly, and option c is the correct option for this problem.
More can be learned about negative and positive association at brainly.com/question/23489661
#SPJ1
The table shows some information about the lifetimes, t, in hours, of some lightbulbs.
Frequency
Lifetime
25
47
50 < t ≤ 100
86
100
45
150 < t ≤ 200
36
200
0
250
37
300 < t ≤ 350
50
Estimate the mean lifetime of a bulb.
Give your answer rounded to 2 DP.
hours
Answers
The estimated mean lifetime of a bulb of 154.69
How to estimate the mean lifetime of a bulb?The table is given as:
Lifetime Frequency
25 < t ≤ 50 47
50 < t ≤ 100 86
100 < t ≤ 150 45
150 < t ≤ 200 36
200 < t ≤ 250 0
250 < t ≤ 300 37
300 < t ≤ 350 50
Calculate the midpoint using:
x = (Lower +Upper)/2
So, we have:
Lifetime Frequency
37.5 47
75 86
125 45
175 36
225 0
275 37
325 50
The mean value is calculated as:
\(\bar x = \frac{\sum fx}{\sum f}\)
So, we have:
\(\bar x = \frac{37.5 * 47 + 75 * 86 + 125 * 45 + 175 * 36 + 225 * 0 + 275 * 37 + 325 * 50}{47 + 86 + 45 + 36 + 0 + 37 + 50}\)
Evaluate
\(\bar x = \frac{46562.5}{301}\)
Divide
\(\bar x = 154.69\)
Hence, the estimated mean lifetime of a bulb of 154.69
Read more about mean at:
https://brainly.com/question/14532771
#SPJ1
What is perimeter of a figure class 6?
Answers
The length of the boundary of any closed figure is called its perimeter.
Perimeter is calculated only of 2-dimensional shape, or a 1-dimensional length. This means that shapes like cubes, cones, and cylinders don't have a perimeter.
The perimeter of any shape is calculated by adding up the length of all its sides. A side is referred to as any continuous uninterrupted length of the shape between two points.
A point to be noted is that the perimeter of a circle is calculated by its radius and a mathematical number called pi. This is denoted by π. All other curved sides are calculated in a similar manner as well.
To know more about perimeter visit
https://brainly.com/question/10153419
#SPJ4
Question 4(Multiple Choice Worth 1 points)
(02.01 LC)
Which of the following does not represent a function?
A
B
C
D
Please help I need this answer right to bring up my grade

Answers
Answer:
c i think
Step-by-step explanation:
A polynomial function has a root of -5 with multiplicity 3, a root of 1 with multiplicity 2, and a root of 3 with multiplicity 7. If the function has a negative leading coefficient and is of even degree, which statement about the graph is true?
A. The graph of the function is positive on (-infinity, -5)
B. The graph of the function is negative on (-5, 3)
C. The graph of the function is positive on (-infinity, 1)
D. The graph of the function is negative on (3, infinity).
Answers
Answer:
D
Step-by-step explanation:
Let's first write the possible function described.
The roots are:
-5 with a multiplicity of 3.
1 with a multiplicity of 2.
And 3 with a multiplicity of 7.
And the leading coefficient is negative.
Therefore:
\(f(x)=-a(x+5)^3(x-1)^2(x-3)^7\)
Where a is a positive value.
We want to know which statement is true about the graph.
First, since the second root is squared, it will always be positive. And since the leading coefficient is negative, our function is now negative.
So, we will only need to test the first and third root, as only they can alter the sign of our function.
Choice A)
(-∞, -5).
Pick any point within this interval. We can use -6 for simplicity. As stated previously, we only need to test the first and third root. We can ignore the exponents as well, since they do not alter signs. Therefore:
\((-6+5)(-6-3)=(-1)(-9)=9>0\)
Since the result is positive, and our function is already negative, our function is negative for (-∞, -5).
A is not correct.
Choice B)
(-5, 3)
Choosing 0:
\((0+5)(0-3)=-15<0\)
Negative times negative is positive. So, f(x) will be positive for (-5, 3).
B is not correct.
Choice C)
(-∞, 1).
Choosing 0, we can see that:
\((0+5)(0-3)=-3<0\)
Negative times a negative is positive. So, it seems that C is correct.
However, notice that the domain (-∞, 1) contains two roots: x = -5 and x = 1.
In reality, we only tested (-5, 1). We have yet to test (-∞, -5). So, by using -6 again:
\((-6+5)(-6-3)=(-1)(-9)=9\)
Positive times negative is negative.
So, f(x) is both positive and negative for (-∞, 1).
C is not correct.
Note: We did not need to double-check for B since it was already false.
Choice D)
(3, ∞)
This only has one root.
And using 4, we see that:
\((4+5)(4-3)=1>0\)
Positive times a negative will be negative.
Hence, f(x) will be negative for (3, ∞).
Choice D is the correct answer.
how to find the turning point of a polynomial function?
Answers
the turning point(s) of a polynomial function by using below steps
To find the turning point of a polynomial function, follow these steps:
1. Determine the degree of the polynomial. The turning point will occur in a polynomial of odd degree (1, 3, 5, etc.) or at most one turning point in a polynomial of even degree (2, 4, 6, etc.).
2. Write the polynomial function in the form f(x) = axⁿ + bxⁿ⁻¹ + ... + cx + d, where n represents the degree of the polynomial and a, b, c, d, etc., are coefficients.
3. Find the derivative of the polynomial function, f'(x), by differentiating each term of the function with respect to x. This will give you a new function that represents the slope of the original polynomial function at any given point.
4. Set f'(x) equal to zero and solve for x to find the x-coordinate(s) of the turning point(s). These are the values where the slope of the polynomial function is zero, indicating a potential turning point.
5. Substitute the x-coordinate(s) obtained in step 4 into the original polynomial function, f(x), to find the corresponding y-coordinate(s) of the turning point(s).
6. The turning point(s) of the polynomial function is given by the coordinates (x, y), where x is the x-coordinate(s) found in step 4 and y is the y-coordinate(s) found in step 5.
By following these steps, you can find the turning point(s) of a polynomial function.
Learn more about polynomial function here
https://brainly.com/question/11298461
#SPJ4
The blood test for determining coagulation activity defects is called the Prothrombin Time (PT) test.
The blood test for determining coagulation activity defects is called the Prothrombin Time (PT) test. This test measures the time it takes for blood to clot and is used to assess the functioning of the clotting factors in the blood. It is commonly used to evaluate the extrinsic pathway of the coagulation cascade, which involves factors outside of the blood vessels.
The PT test is an important diagnostic tool in hematology and is used to diagnose or monitor conditions that affect blood clotting, such as bleeding disorders or the effectiveness of anticoagulant medications. By measuring the PT, healthcare professionals can determine if there are any abnormalities in the coagulation process and make appropriate treatment decisions.
Learn more:About blood test here:
https://brainly.com/question/31576763
#SPJ11
g What day of the week was there the most crime? Does the day of the week effect the crime rate?
Answers
The day of the week with the most crime is [insert the day with the highest crime rate]. The day of the week does have an effect on the crime rate, as certain days may exhibit higher crime rates compared to others.
The analysis of crime data reveals patterns and trends that can help identify the day of the week when crime incidents are most prevalent. Law enforcement agencies and researchers often analyze crime statistics to understand the dynamics of criminal activity. By examining crime rates across different days of the week, they can identify any correlations or trends.
Factors such as social behaviors, economic conditions, and routine activities can influence crime rates on specific days. For example, weekends might see higher crime rates due to increased social gatherings and leisure activities, while weekdays may experience different patterns driven by work schedules and routines.
Additionally, factors like alcohol consumption, events, or cultural practices can also contribute to variations in crime rates on specific days.
Understanding the relationship between the day of the week and crime rate can inform law enforcement strategies, resource allocation, and community safety initiatives. By focusing resources and efforts during periods of heightened crime rates, authorities can work towards crime prevention and reduction.
Learn more about Crime rates
brainly.com/question/31810991
#SPJ11
Rotate the following point (- 5, 7) with a 90 degree CCW rotation
Answers
Given:
The point is (-5,7).
To find:
The image of the given point after 90 degrees counter clockwise rotation.
Solution:
If a point rotated 90 degrees counter clockwise, then
\((x,y)\to (-y,x)\)
Let the given point is P(-5,7). Using the above rule, we get
\(P(-5,7)\to P'(-7,-5)\)
Therefore, the image of the given point after 90 degrees counter clockwise rotation is (-7,-5).