Answers
Answer:
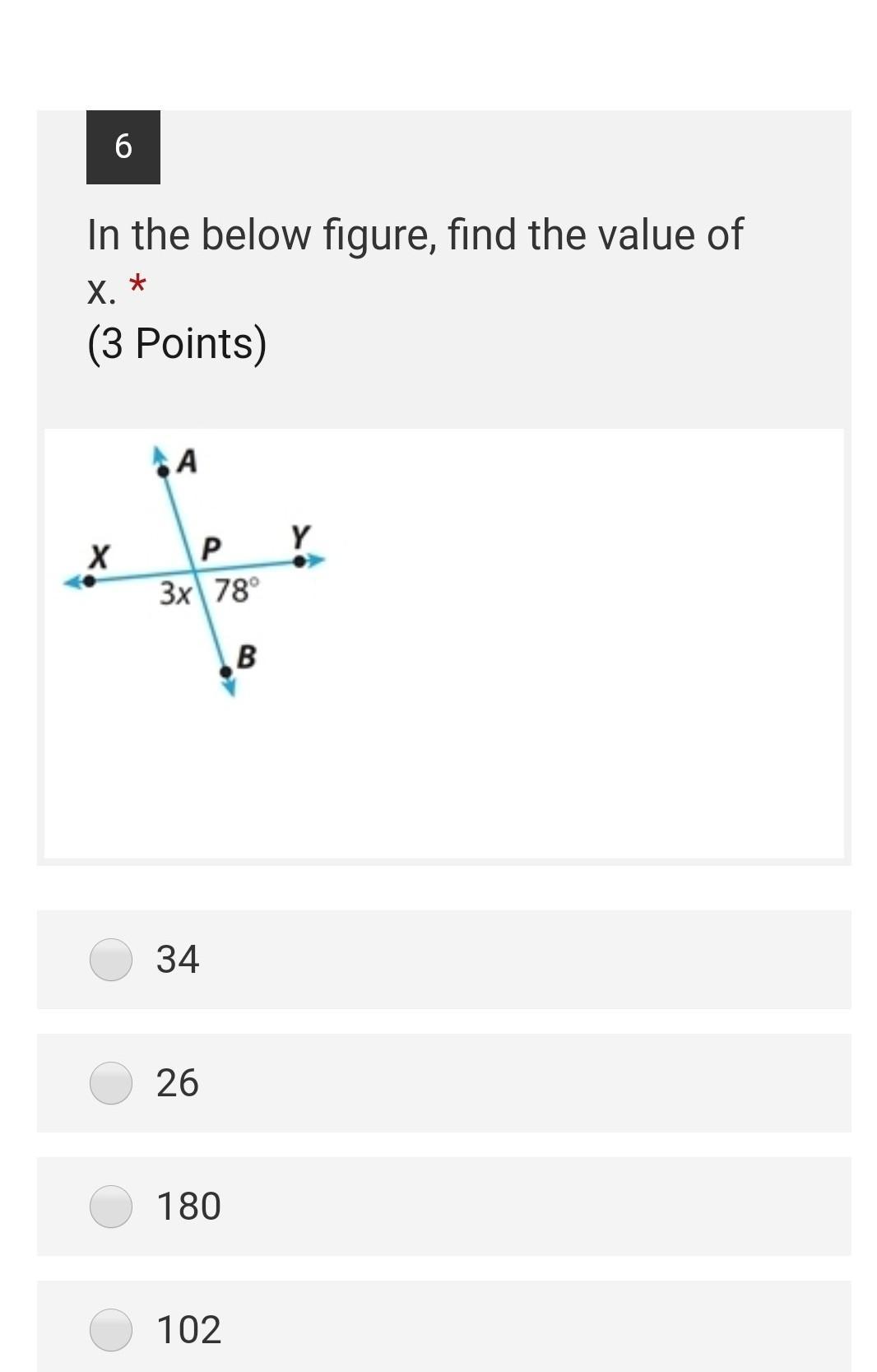
34
Step-by-step explanation:
angles YPB and BPX together form 180 degrees
180 - 78 = 3x
102/3 = x
x = 34
This is because if you take 180-78 you would get 102. And because you are trying to solve for x you would have to take 102 and divide it by 3 which gives you 34
Related Questions
2d²y/dx² + yd²y/dx² = 0, dy/dx at x = 0 = 0, dy/dx at x = infinite = 1, dy/dx at x = 5 = 0.99 d²z/dx² + k/2y dz/dx = 0 z(0) = 0 and z(infinite) = 1 k is just a constant. Solve the differential equations with boundary conditions. By using Runge kutta4 method with MATLAB
Answers
Adjust the parameters as needed, such as the step size (h) and the final x-value (xn), and run the code to obtain the solution for y(x).
The resulting plot will show the solution curve.
To solve the given set of differential equations using the Runge-Kutta method in MATLAB, we need to convert the second-order differential equations into a system of first-order differential equations.
Let's define new variables:
y = y(x)
z = dz/dx
Now, we have the following system of first-order differential equations:
dy/dx = z (1)
dz/dx = -k/(2y) (2)
To apply the Runge-Kutta method, we need to discretize the domain of x. Let's assume a step size h for the discretization. We'll start at x = 0 and proceed until x = infinite.
The general formula for the fourth-order Runge-Kutta method is as follows:
k₁ = h f(xn, yn, zn)
k₂ = h f(xn + h/2, yn + k₁/2, zn + l₁/2)
k₃ = h f(xn + h/2, yn + k₂/2, zn + l₂/2)
k₄ = h f(xn + h, yn + k₃, zn + l₃)
yn+1 = yn + (k₁ + 2k₂ + 2k₃ + k₄)/6
zn+1 = zn + (l₁ + 2l₂ + 2l₃ + l₄)/6
where f(x, y, z) represents the right-hand side of equations (1) and (2).
We can now write the MATLAB code to solve the differential equations using the Runge-Kutta method:
function [x, y, z] = rungeKuttaMethod()
% Parameters
k = 1; % Constant k
h = 0.01; % Step size
x0 = 0; % Initial x
xn = 10; % Final x (adjust as needed)
n = (xn - x0) / h; % Number of steps
% Initialize arrays
x = zeros(1, n+1);
y = zeros(1, n+1);
z = zeros(1, n+1);
% Initial conditions
x(1) = x0;
y(1) = 0;
z(1) = 0;
% Runge-Kutta method
for i = 1:n
k1 = h * f(x(i), y(i), z(i));
l1 = h * g(x(i), y(i));
k2 = h * f(x(i) + h/2, y(i) + k1/2, z(i) + l1/2);
l2 = h * g(x(i) + h/2, y(i) + k1/2);
k3 = h * f(x(i) + h/2, y(i) + k2/2, z(i) + l2/2);
l3 = h * g(x(i) + h/2, y(i) + k2/2);
k4 = h * f(x(i) + h, y(i) + k3, z(i) + l3);
l4 = h * g(x(i) + h, y(i) + k3);
y(i+1) = y(i) + (k1 + 2*k2 + 2*k3 + k4) / 6;
z(i+1) = z(i) + (l1 + 2*l2 + 2*l3 + l4) / 6;
x(i+1) = x(i) + h;
end
% Plotting
plot(x, y);
xlabel('x');
ylabel('y');
title('Solution y(x)');
end
function dydx = f(x, y, z)
dydx = z;
end
function dzdx = g(x, y)
dzdx = -k / (2*y);
end
% Call the function to solve the differential equations
[x, y, z] = rungeKuttaMethod();
Learn more about differential equations click;
https://brainly.com/question/32645495
#SPJ4
what is a congruent polygon
Answers
A congruent polygon refers to two or more polygons that have the same shape and size. There must be an equal number of sides between two polygons for them to be congruent.
Congruent polygons have parallel sides of equal length and parallel angles of similar magnitude. When two polygons are congruent, they can be superimposed on one another using translations, rotations, and reflections without affecting their appearance or dimensions. Concluding about the matching sides, shapes, angles, and other geometric properties of congruent polygons allows us to draw conclusions about them.
Learn more about Congruent polygons here:
https://brainly.com/question/2096633
#SPJ1
The model is shaded to represent the remaining one-half of a cake. Three friends will
each receive an equal amount of the remaining cake until it is all gone.
Cake
Which equation can be used to determine the fraction of the whole cake each friend
will receive?
Answers
Answer:
jsjshshshhsgdhshdhdhddhshggzggzgzhshsggggghzhgzgzgdgxgshdhdhgd
Step-by-step explanation:
h
Answer:
h
Step-by-step explanation:
Solve for x. Show your work with proper statements and notation.
a
Point O ∈
AB

Answers
Answer:
x=27
Step-by-step explanation:
m<AOB = 180
36+90+2x=180
x=27 degrees
Exercise Price Call Price Put Price
120 15.40 9.25
125 13.50 11.50
130 11.35 14.25
The underlying stock is currently price at $125.94
For each option strategy make sure to graph the position and label breakeven stock prices, maximum profit, and minimum profit.
Construct a butterfly spread using the three calls available.
Answers
The butterfly spread is constructed using the following three calls: - Buy 1 call with an exercise price of 120 at a price of $15.40.- Sell 2 calls with an exercise price of 125 at a price of $13.50 each.- Buy 1 call with an exercise price of 130 at a price of $11.35.
A butterfly spread involves buying one option with a lower exercise price, selling two options with a middle exercise price, and buying one option with a higher exercise price. In this case, we buy the call with an exercise price of 120, sell two calls with an exercise price of 125, and buy the call with an exercise price of 130.
To analyze the strategy, we need to consider the stock price at expiration. The breakeven stock prices are calculated by adding and subtracting the net debit or credit from the middle exercise price. In this case, the net debit is $1.60 ($15.40 – 2*$13.50 + $11.35), so the breakeven prices are $121.40 ($125 - $1.60) and $128.60 ($125 + $1.60).
The maximum profit of $1.60 occurs when the stock price is exactly at the middle exercise price of 125 at expiration. In this case, the two sold calls expire worthless, and the two bought calls have intrinsic value of $5 each. The minimum profit of -$1.40 occurs when the stock price is below $121.40 or above $128.60 at expiration. In this situation, all the options expire worthless, resulting in a loss of the net debit.
Learn more about Butterfly spread here: brainly.com/question/32201277
#SPJ11
Select all the statements that are true about rectangles
Answers
The statements that are true about rectangles are mentioned in options
A,B,C,E.
Rectangles -A shape with four sides and internal angles is a rectangle. The lengths of the other two sides are offset by two. The rectangle's diagonal sides are of identical length.
The opposite sides of a rectangle are equal and parallel to one another.
The diagonals cut each other in half, but not exactly.
All diagonals are the same length.
The rectangle's diagonals line up.
The total internal angles add up to the same value
Every internal angle has the same value.
A rectangle has congruent angles on all sides.
A rectangle's opposing angles are congruent.
We may thus infer that the statements about rectangles in the options are accurate based on the aforementioned features.
Q. Select all the statements that are true about rectangles.
A Diagonals are congruent.
B Diagonals bisect angles.
C Opposite angles are congruent.
D Diagonals are perpendicular.
E Diagonals bisect each other.
To know more about rectangle click here
https://brainly.com/question/22466576
#SPJ4
Graph four points that satisfy the equation y=-x-2
Answers
Step-by-step explanation:
plug in variables for x
x= 1:
-(1)-2
y= -3
x=2
-(2)-2
y= -4
x=3
-(3)-2
y= -5
x=4
-(4)-2
y= -6
What is the products? (2t+1)(t-4)
Answers
Step-by-step explanation:
hsusbdjdhssjzssisbzjshzbzbaizussbissbisbsisbsssj
if you traveled in space at a speed of 1000 miles per house, how far would you travel in 7.5*10^5 houes
Answers
Traveling at a speed of 1000 miles per hour for 7.5 * 10⁵ hours would result in traveling a distance of 7.5 * 10⁸ miles.
To calculate the distance traveled, we can multiply the speed by the time traveled.
Speed = 1000 miles per hour
Time = 7.5 * 10⁵ hours
Distance = Speed * Time
Distance = 1000 miles/hour * 7.5 * 10⁵ hours
To perform this calculation, we can multiply the numerical values and keep the scientific notation for the result:
Distance = 1000 * 7.5 * 10⁵ miles
Distance = 7.5 * 10⁸ miles
Therefore, traveling at a speed of 1000 miles per hour for 7.5 * 10⁵ hours would result in traveling a distance of 7.5 * 10⁸ miles.
Learn more about Distance here
https://brainly.com/question/18815731
#SPJ4
onsider the following two probability distributions: Distribution A Distribution
B x P(x) x P(x)
0 0.20 0 0.01
1 0.20 1 0.02
2 0.20 2 0.94
3 0.20 3 0.02
4 0.20 4 0.01
Which of the following is an accurate statement regarding these two distributions?
Distribution A has a higher variance.
Distribution B has a higher variance.
Both distributions are positively skewed.
Both distributions are uniform.
Answers
The accurate statement regarding these two distributions is that Distribution A has a higher variance, and both distributions are positively skewed.
To determine which distribution has a higher variance, we need to calculate the variance of each distribution. Recall that the variance is given by the formula:
Var(X) = E[(X - μ)²],
where E is the expected value operator and μ is the mean of the distribution.
For Distribution A, we have:
μ = 0(0.20) + 1(0.20) + 2(0.20) + 3(0.20) + 4(0.20) = 2
E[(X - μ)²] = (0 - 2)²(0.20) + (1 - 2)²(0.20) + (2 - 2)²(0.20) + (3 - 2)²(0.20) + (4 - 2)²(0.20) = 2
For Distribution B, we have:
μ = 0(0.01) + 1(0.02) + 2(0.94) + 3(0.02) + 4(0.01) = 2
E[(X - μ)²] = (0 - 2)²(0.01) + (1 - 2)²(0.02) + (2 - 2)²(0.94) + (3 - 2)²(0.02) + (4 - 2)²(0.01) = 1.24
Therefore, Distribution A has a higher variance than Distribution B.
Regarding the skewness, we can observe that Distribution A and Distribution B are not symmetric, but have a mode at 2, and the probabilities decrease as we move away from the mode. Therefore, both distributions are positively skewed.
For more similar questions on probability:
brainly.com/question/13604758
#SPJ11
Find the area of the roof of the gazebo in problem 25, if each roof ridge is 10ft long, as shown

Answers
Check the picture below.
first off let's check what "h" is in the triangular face.
\(\textit{using the pythagorean theorem} \\\\ c^2=a^2+b^2 \qquad \begin{cases} c=\stackrel{hypotenuse}{10}\\ a=\stackrel{adjacent}{6}\\ b=\stackrel{opposite}{h}\\ \end{cases}\implies 10^2=6^2+h^2 \\\\\\ 10^2-6^2=h^2\implies \sqrt{10^2-6^2}=h\implies 8=h\)
so, the gazebo has 4 squarish faces, each 12x12, recall 48 ÷ 4 = 12, and it has 4 triangular faces, each with a height of 8 and a base of 12.
notice we're skipping the top and bottom of the cube and the bottom of the pyramid because they're not part of the "surface area".
\(\stackrel{\textit{\large Areas}}{\stackrel{\textit{4 triangular faces}}{4\left[\cfrac{1}{2}(12)(8) \right]}~~~~+~~~~\stackrel{\textit{4 squarish faces}}{4[12\cdot 12]}}\implies 192+576\implies 768\)

A Company Is Afraid They Are Spending Too Much On The Production Of Some Small Cans They Use. The Current Cans Hold 80 Ml. If The Bottom Of The Can Costs $0.02 Per Cm², The Top Costs $0.01 Per Cm² And The Side Of The Can Costs $0.009 Per Cm², How Much Is The Cheapest Can That Holds The Required Amount? (1 Ml = 1 Cm³ )[3]
Answers
To determine the cheapest can that holds the required amount, we need to calculate the total cost of the can based on the costs of the different components (bottom, top, and side) and their respective surface areas.
The surface area of the bottom is given by the formula for the area of a circle, which is A_bottom = πr². The surface area of the top is also A_top = πr². The surface area of the side is given by the formula for the lateral surface area of a cylinder, which is A_side = 2πrh. To hold the required volume, we have the equation V = πr²h. We need to minimize the cost function C = 0.02A_bottom + 0.01A_top + 0.009A_side. Substituting the expressions for the surface areas and simplifying, we get C = 0.03πr² + 0.018πrh.
Using the equation for the required volume, we can express the height in terms of the radius as h = V / (πr²).
Substituting this expression for h into the cost function, we have C = 0.03πr² + 0.018πr(V / (πr²)) = 0.03πr² + 0.018V / r.
To find the minimum cost, we take the derivative of C with respect to r, set it equal to zero, and solve for r:
dC/dr = 0.06πr - 0.018V / r² = 0.
Simplifying the equation, we get 0.06πr³ - 0.018V = 0.
Solving for r, we find r³ = V / (0.06π).
Taking the cube root of both sides, we have r = (V / (0.06π))^(1/3).
Learn more about the lateral surface area here: brainly.com/question/2285144
#SPJ11
Jim is swimming part of a lap around his 100-foot diameter pool. If he swims around the outside edge, how far does he swim if he travels a 60° arc, rounded to the nearest foot? Use 3.14 for pi.
Answers
answer:
have any notes for reference?
Step-by-step explanation:
A car drives 120 miles in 3 hours.
Calculate the average speed, in mph, of the car.
Answers
Answer:
40 mph per hour
Step-by-step explanation:
120/3=40
ILL MARK U BRAINLIEST!

Answers
Answer:
D
Step-by-step explanation:
please brainliest me
The diagram shows an open rectangular box ABCDEFGH.
A straight stick AGM rests against A and G and extends outside the box to M.
a. Calculate the angle between the stick and the base of the box.
b. AM= 30 cm.
Show that GM= 4.8 cm, correct
to 1 decimal place.

Answers
The angle between the stick and the base of the box is 77. 9 degrees
How to determine the angleTo determine the angle between the stick and the base, we have to know the trigonometric identities.
These identities are;
sinecosinecotangenttangentsecantcosecantFrom the information given, we have;
sin A = FB/AB
Given that;
GB = 14.5cm
AB = 18. 6cm
substitute for the length of the sides, we have;
sin A = 14.5/18. 6
Divide the values, we have;
sin A = 0. 7796
Find the inverse sine
A = 77. 9 degrees
Learn more about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
12. In a laboratory experiment, Amoeba A lives 5 hours longer than Amoeba B, and Amoeba B lives twice as long as Amoeba C. If n is the lifespan of Amoeba C in hours, what is the lifespan of Amoeba A, in terms of?
Answers
The lifespan of Amoeba A, in terms of amoeba C is 5 + 2n
AlgebraAmoeba A life span = 5 + amoeba BAmoeba B life span = 2(amoeba C life span)Amoeba C life span = nSo,
Amoeba B life span = 2(amoeba C life span)
= 2(n)
= 2n
Amoeba A life span = 5 + amoeba B
= 5 + 2n
Therefore, the lifespan of Amoeba A, in terms of amoeba C is 5 + 2n
Learn more about algebra:
https://brainly.com/question/6143254
#SPJ1
It’s sad when I help people because they don’t do the same thing to so please please please... answer me once :((((((((((((((((((((((((((((((((((((((((((((((
Answers
Answer:
Where is the question????????
Friend
What's your question, my friend?
What are the two ratios that are equivalent to 2:9

Answers
Answer:
bc
Step-by-step explanation:
2:9 is equivalent to
18: 81 because is 2*9 : 9*9
12:54 because is 2*6 : 9* 6
How can you determine whether the data in a table represents a proportional relationship? *
Answers
Answer:
\(this \: can \: be \: done \: by \: appling \: the \to \\ rate \: of \: change \: law : \\ r.o.c \: (m) = \frac{y_{2} -y_{1} }{x_{2} -x_{1} } \)
a plane flies 360 miles against the wind in 2 hours 15 minutes, while on its return trip it takes 1 hour 30 minutes with the same wind. determine the air speed of the plane.
Answers
The air speed of the plane to cover 360 miles against the wind and with the wind in the given time is equal to 200 miles per hour.
Let 'x' be the speed of the plane fly in still air.
And 'y' be the speed of the wind.
Speed against the wind = x - y
Speed with the wind = x + y
Total distance covered by plane = 360 miles
Time taken against the wind = 2 hours 15 minutes
= 2 ( 1/4 ) hours
= 9 / 4 hours
Time taken with the wind = 1 hour 30 minutes
= 1 ( 1/2 ) hours
= 3 /2 hours
Speed = distance / time
Against the wind :
x - y = 360 / (9 /4 )
⇒x - y = 160___(1)
With the wind:
x + y = 360 / (3 /2)
⇒x + y = 240 ___(2)
Add (1) and (2) we get,
2x = 400
⇒ x= 200miles per hour
⇒y = 40 miles per hour
Therefore, the air speed of the plane as per given condition is equal to 200miles per hour.
Learn more about speed here
brainly.com/question/7359669
#SPJ4
Factor the following expression completely: 3x}(3x - 4)2 + x^(8)(3x - 4)(3). O 8x?(3x - 4)(6x - 12) O 24x}(3 x - 4)(11x - 12) O 3x3(3x - 4)(11x - 4) Ox}(3x – 4)(11x - 4) O 3x3 (3x - 4)(3x + 4)
Answers
Option D, 3x^3(3x - 4)(11x - 4), is not a correct factorization of the given expression.
We are given the expression:
3x(3x - 4)^2 + x^8(3x - 4)(3)
We can first factor out the common factor of (3x - 4) from both terms, giving us:
(3x - 4)[3x(3x - 4) + x^8(3)]
Simplifying the expression inside the square brackets, we get:
(3x - 4)[9x^2 - 12x + 3x^8]
Now, we can factor out 3x^2 from the expression inside the square brackets, giving us:
(3x - 4)[3x^2(3x^6 - 4) + 3]
We can simplify further by factoring out 3 from the expression inside the square brackets, giving us:
(3x - 4)[3(x^2)(3x^6 - 4) + 1]
Therefore, the fully factored expression is:
3x(3x - 4)^2 + x^8(3x - 4)(3) = (3x - 4)[3(x^2)(3x^6 - 4) + 1]
Learn more about factorization here
https://brainly.com/question/18187355
#SPJ11
Calculate each Poisson probability: a. P(X = 7), λ = 6 (Round your answer to 4 decimal places.) b. P(X = 11), λ = 12 (Round your answer to 4 decimal places.) c. P(X = 6), λ = 8 (Round your answer to 4 decimal places.)
Answers
P(X = 7), λ = 6: The Poisson probability of X = 7, with a parameter (λ) value of 6, is 0.1446. P(X = 11), λ = 12: The Poisson probability of X = 11, with a parameter (λ) value of 12, is 0.0946. P(X = 6), λ = 8: The Poisson probability of X = 6, with a parameter (λ) value of 8, is 0.1206.
The Poisson probability is used to calculate the probability of a certain number of events occurring in a fixed interval of time or space, given the average rate of occurrence (parameter λ). The formula for Poisson probability is P(X = k) = (e^-λ * λ^k) / k!, where X is the random variable representing the number of events and k is the desired number of events.
To calculate the Poisson probabilities in this case, we substitute the given values of λ and k into the formula. For example, for the first case (a), we have λ = 6 and k = 7: P(X = 7) = (e^-6 * 6^7) / 7!
Using a calculator, we can evaluate this expression to find that the probability is approximately 0.1446. Similarly, for case (b) with λ = 12 and k = 11, and for case (c) with λ = 8 and k = 6, we can apply the same formula to find the respective Poisson probabilities.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
which function is increasing on the interval (-∞, ∞)

Answers
Differentiating each function, we have for all x, unless otherwise indicated,
\(h(x) = 2^x - 1 \implies h'(x) = \ln(2) \, 2^x > 0\)
\(g(x) = -4 (2^x) \implies g'(x) = -4 \ln(2) \, 2^x < 0\)
\(f(x) = -3x+7 \implies f'(x) = -3 < 0\)
\(j(x) = x^2 + 8x + 1 \implies j'(x) = 2x + 8 > 0 \text{ only when } x > -4\)
and only h(x) has a strictly positive derivative. (A)
Using the standard normal table, the probability that Seth’s light bulb will last no more than 14,500 (P(z ≤ 1.25)) hours is about
Answers
Answer:
How many standard deviations above the mean is 14,500 hours? 1.25 1.5 2.5 Using the standard normal table, the probability that Seth's light bulb will last no more than 14,500 (P(z ≤ 1.25)) hours is about ✔ 89% .
Answer:
89%
Step-by-step explanation:
brainliest please
Micah wants to insert a photo on his website. The current size of the photo is 1,800 pixels by 1,200 pixels. He wants to reduce the
photo to 450 pixels by 300 pixels. What is the scale factor of the reduction?
Answers
Write an equation in slope-intercept form of the line that passes through the given point and is parallel to the graph of the given equation
(-7,-6); y = - 4x + 4
Answers
Answer:
y = -4x-34
Step-by-step explanation:
From the line to which the line is parallel, we can get the slope
The general form of a linear model is;
y = mx + b
where m
is the slope and b is the y-intercept
From the question, using the given line,
we have the slope of that line as -4
Now, we want to write the equation of a line that passes through (-7,-6) and has a slope of -4
we can use the point-slope form
for this
That would be;
y-y1 = m(x-x1)
y + 6 = -4(x+ 7)
y + 6 = -4x -28
y = -4x -28-6
y = -4x - 34
HELP PLS
What is the next term of the following sequence? 20, 10, 5, 2, 1/2 ...
A:3/4
B:1 1/2
C:1 1/4
Answers
Answer:
I'm thinking it's A...
==================================================
Explanation:
I'm assuming you meant to say 2 & 1/2 instead of 2,1/2
If so, then we cut that last term 2 & 1/2 in half
The whole part 2 cuts in half to 1
The fractional part 1/2 cuts in half to 1/4
2 & 1/2 cuts in half to 1 & 1/4 which leads to choice C
The reason why we cut in half is because the jump from 20 to 10 is "divide by 2", and the same applies from 10 to 5, and from 5 to 2 & 1/2.
every answer I have typed in is wrong but what is.
2/12 simplified
Answers
Answer:
1/6
Step-by-step explanation:
hope this helps :)
1/6
divide both by 2 and you get 1/6
Type the correct answer in each box. Use numerals instead of words.
Harry buys a boat in 2010. He plans on selling it in 2020. In 2010, the boat costs $20,000. The value of the boat depreciates over time
as is shown in the graph below, where the y-axis represents the value of the boat, in dollars, and the x-axis represents the number of
years since 2010.

Answers
Answer:
The initial value of the boat was $20,000
The percent decrease per year of the value of the boat is 10%.
The interval on which the value of the boat is decreasing while Harry has it is (0,10)
Step-by-step explanation:
It is given that the boat costs $20,000 in 2010 when x = 0. So, the initial value of the boat was $20,000.
Next, find the percent decrease per year of the value of the boat. Consider the general form of an exponential equation, y = a(b)x, where a is the initial value of the boat, b is the base of the exponent, x is the number of years after 2010, and y is the value of the boat, in dollars.
Consider the point (1 , 18,000) which lies on the graph of this situation. Substitute x = 1, y = 18,000, and a = 20,000 into the exponential equation and isolate b.
Recall that for exponential decay, b = 1 - r where r represents the decay rate. Substitute b = 0.9 into this equation and solve for r.
So, the decay rate is 0.1, and the percent decrease per year of the value of the boat is 10%.
Harry bought the boat in 2010, and plans on selling it after 10 years in 2020. Therefore, the interval on which the value of the boat is decreasing while Harry has it is [0, 10].