Answers
Answer:
b is the correct answer
hope it helps please fo llow me
Related Questions
Assume your favorite football team has 2 games left to finish the season. The outcome of each game can be win, lose or tie. The number of possible outcomes is
a. 2
b. 4
c. 6
d. None of the other answers is correct.
Answers
The number of possible outcomes for each game is 3 (win, lose, or tie). Since there are 2 games left, the total number of possible outcomes is 3 x 3 = 9. Therefore, none of the given answers (a, b, or c) is correct. The correct answer is d.
To determine the number of possible outcomes for your favorite football team's remaining 2 games, we'll consider each game independently. Each game can have 3 possible outcomes: win, lose, or tie. For 2 games, you can use the multiplication principle:
Number of possible outcomes = Outcomes for Game 1 × Outcomes for Game 2
So, the number of possible outcomes is:
3 (win, lose, or tie in Game 1) × 3 (win, lose, or tie in Game 2) = 9
Since 9 is not among the given options, the correct answer is:
d. None of the other answers is correct.
To learn more about possible outcomes, click here:
brainly.com/question/27292589
#SPJ11
Please please help me with this. i beg uuuuu!!!

Answers
Answer:
a) 63
Step-by-step explanation:
Help me I need this quick

Answers
Answer:
I think 3,9, and 15
Step-by-step explanation:
Use the subtraction property of equality to write 3 equations that have the same solution of x=12
Answers
The equations are x - 5 = 7, x - 7 = 5 and x - 4 = 8
How to determine the equationsThe solution to the equation is given as
x = 12
The subtraction property of equality states that if we subtract the same number from both sides of an equation, the equation remains true.
Using the above as a guide, we have the following:
x - 4 = 12 - 4 (subtract 4 from both sides)x - 5 = 12 - 5 (subtract 5 from both sides)x - 7 = 12 - 7 (subtract 7 from both sides)Each of these equations is equivalent to x = 12, since we have simply subtracted the same value from both sides of the equation.
Hence, the solution to each of these equations is x = 12.
Read more about equations at
https://brainly.com/question/2972832
#SPJ1
a. Find the derivative function f′ for the function f. b. Determine an equation of the line tangent to the graph of f at (a,f(a)) for the given value of a. f(x)=√5x+1,a=7 a. f′(x)=
Answers
The derivative function f'(x) for the function f(x) = √(5x + 1) is (5/2)√(5x + 1).
The derivative function f'(x) of the given function f(x) = √(5x + 1), we can apply the power rule and chain rule of differentiation.
Using the power rule, we differentiate the square root term as (1/2) * (5x + 1)^(-1/2), and then apply the chain rule by multiplying it with the derivative of the inner function 5x + 1, which is 5.
So, f'(x) = (1/2) * (5x + 1)^(-1/2) * 5.
Simplifying further, we get:
f'(x) = (5/2) * (5x + 1)^(-1/2).
Therefore, the derivative function f'(x) for the given function f(x) = √(5x + 1) is (5/2)√(5x + 1).
For part b, to determine the equation of the tangent line to the graph of f at the point (a, f(a)), we substitute the value of a into the derivative function f'(x) and evaluate it at that point.
Learn more about multiply : brainly.com/question/620034
#SPJ11
Which pair of data sets shows no overlap?
A. A1: 23, 27, 23, 28, 24, 25, 23, 22,
29, 20
A2: 28, 26, 30, 32, 35, 25, 28, 33,
39, 31
B. B1: 7.5, 10, 12, 8.5, 9.2, 14.9, 6.8,
11, 13.5, 7.5
B2:15, 13.4, 14, 12.9, 9.5, 14.5, 7.1,
11.2, 10, 13.5
C. C1: 12.0, 24.1, 36.0, 18.2, 35.1, 15.9,
11.9, 16.2, 14.4, 28.7
C2: 7.5, 4.8, 8.9, 11.5, 11.8, 10.8,
4.9, 6.0, 10.4, 11.8, 8.4
D. D1: 3.2, 5.5, 3.9, 2.1, 4.3, 2.8, 3.8,
4.5, 4.9, 3.2
D2: 5:8, 7.4, 5.2, 6.5, 4.3, 8.7, 3.5,
9.4, 7.2, 4.6
Answers
Answer: D
Step-by-step explanation:
The first data set, D1, has values ranging from 2.1 to 5.5, while the second data set, D2, has values ranging from 3.5 to 9.4. Since there is no overlap between the ranges of values in D1 and D2, these data sets show no overlap. In contrast, data sets A, B, and C all have overlapping ranges of values.
The ratio of the interior angle measures of a triangle is 2:3:5. What are the angle measures? In order from least to greatest, the angle measures are
Answers
Answer:
36, 54, 90
Step-by-step explanation:
angle ratio = total internal angles
2x + 3x +5x = 180
10x = 180
x = 18
2×18:3×18:5×18
36, 54, 90
A Choose any two functions. Explain how to find the domain and range of: • the composition of the functions, • sum and difference of the functions, and product and quotient of the functions.
Answers
Two functions are,
⇒ f(x) = 3x and g(x) = x
Now, Let's take f(x) = 3x and g(x) = x as two functions.
1) To determine the domain and range of the composition of functions, f(g(x)), we must first evaluate g(x), after which we must insert the result into f(x).
Consequently, f(g(x)) = f(x) = 3x
and g(x) = x.
The collection of all x values found in the domain of g(x) is the domain of f(g(x)).
The domain of g(x) is all real numbers in this situation.
Hence, As a result, all real numbers are included in f(g(x))'s domain.
The set of all possible values for f(g(x)) is referred to as the function's range. Since the square of any real number is never negative, the range of f(g(x)) is also the range of non-negative real numbers.
2) The domain and range of the sum and difference of functions, f(x) + g(x) and f(x) - g(x), may be determined by examining the domain and range of each function independently.
The domains of f(x) and g(x) come together to form the domain of f(x) + g(x) and f(x) - g(x).
Both functions in this situation have as their domain all real numbers. Therefore, all real numbers are included in the domain of both f(x) + g(x) and f(x) - g(x).
f(x) and g(x) values determine the range of f(x) + g(x) and f(x) - g(x). All real numbers fall within f(x)'s range, and all non-negative real numbers fall within g(x)'s range. Consequently, all real numbers fall inside the range of f(x) + g(x).
3) Since division by zero is undefined, we must take into account g(x)'s zeros in order to determine the domain and range of the product and quotient of functions, f(x)*g(x) and f(x)/g(x).
The point where the domains of f(x) and g(x) cross is called the domain of f(x) g(x). The domain of f(x) g(x) is therefore limited to real integers alone.
All x values, except the zeros of g(x), are included in the domain of f(x)/g(x). G(x) has zeros when x = 0 since it equals x. All real values, excepting x = 0, are therefore included in the domain of f(x)/g(x).
Based on the values of f(x) and g(x), the range of f(x) g(x) and f(x) / g(x) is determined. F(x) has a real-only domain.
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ1
If the simple interest on $3000 for 7 years is 840$, then what is the interest rate?
Answers
Answer:
Step-by-step explanation:
4%
What is 16/64 simplified?
Answers
Answer:
1/2
Step-by-step explanation:
16/64 (divide the numerator and denominator by 4)
-> 4/8 (divide the numerator and denominator by 4)
-> 1/2
if
f(x)=4x2−3x+7 , what is f(−2) ?
Answers
Answer:
D. 29 I just know the awnser sorry
To find the value of f(−2), we substitute −2 for x in the function f(x):
f(−2) = 4(-2)^2 − 3(-2) + 7
= 4(4) − 3(2) + 7
= 16 − 6 + 7
= 11
Therefore, f(−2) = 11.
. The length of a square board is (5x+3). Find the area of the board. Hint: Formula A=l*w
Answers
Answer:
64
Step-by-step explanation:
Answer:
A = 25x^2 + 30x + 9
Step-by-step explanation:
A = (5x+3) * (5x+3) or A = (5x+3)^2
A = 5x*5x + 5x*3 + 5x*3 + 3*3
A = 25x^2 + 15x + 15x + 9
A = 25x^2 + 30x + 9
If m < 0 and b > 0, the graph of y = mx + b does not pass through which quadrant?
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
Answers
Answer: Quadrant III
Step-by-step explanation:
The slope is negative and the y-intercept is positive.
This means that it is impossible for both x and y to be negative, and thus it does not pass through Quadrant III
Four friends all five each other presents
The total cost of presents is £80.52
Work out the mean cost of presents in pounds
Answers
Step-by-step explanation:
Four friends all give each other presents. The total cost of the presents is £80.52. We need to find the mean cost of a present in pounds. So, the mean cost of a present is equal to 20.13 .
find the equations of the normal line to the surface z = 2 x 4 y 7 z=2x4y7 at the point ( − 1 , 1 , 2 )
Answers
Answer:
Step-by-step explanation:
To find the equation of the normal line to the surface z = 2x^4y^7 at the point (-1,1,2), we need to find the gradient of the surface at that point.
The gradient of a surface is a vector that points in the direction of the steepest increase in the surface, and its magnitude is the rate of change of the surface in that direction. To find the gradient, we take the partial derivatives of the surface with respect to each variable and form a vector:
∇f = ( ∂f/∂x, ∂f/∂y, ∂f/∂z )
For z = 2x^4y^7, we have:
∂f/∂x = 8x^3y^7
∂f/∂y = 28x^4y^6
∂f/∂z = 0
So, at the point (-1,1,2), the gradient is:
∇f = ( ∂f/∂x, ∂f/∂y, ∂f/∂z ) = ( 8(-1)^3(1)^7, 28(-1)^4(1)^6, 0 ) = (-8,28,0)
This means that the normal to the surface at the point (-1,1,2) is the vector (-8,28,0). To find the equation of the normal line, we can use the point-normal form of the equation of a line:
(x - x0)/a = (y - y0)/b = (z - z0)/c
where (x0, y0, z0) is the point on the line, and (a, b, c) is the direction vector of the line.
In this case, we have:
(x + 1)/(-8) = (y - 1)/28 = (z - 2)/0
Since the z-component of the direction vector is 0, we can drop the last term in the equation. Solving for x and y, we get:
x = -1 - (1/4)y
y = 1 + 28/8t
where t is a parameter that can take any value. So the equation of the normal line is:
x = -1 - (1/4)y
y = 1 + 28/8t
z = 2
or in parametric form:
r(t) = (-1 - (1/4)(1 + 28/8t))i + (1 + 28/8t)j + 2k
What is the expected value of M?
A)
It is the sample mean.
B)
It is the sample standard deviation.
C)
It is the mean of the distribution of sample means.
D)
It is the standard deviation of the distribution of sample means.
Answers
The expected value of M is described as C: "it is the mean of the distribution of sample means.
In probability theory, the expected value of M is a generalization of the weighted average. In informal words, the expected value refers to the arithmetic mean of a large sample of independently chosen outcomes of a random variable.
Thus, the mean of the distribution of sample means is referred to as the 'expected value' of M. And it is always equal to the mean μ of the population. So the correct answer pertaining to this question is held in option 'C'.
You can learn more about expected value at
https://brainly.com/question/14723169
#SPJ4
write an equation in slope intercept form for the line that passes through (5,-1) (6,-1)
Answers
Slope intercept form:
(y2-y1)/(x2-x1)
(-1-(-1)/(6-5)=
0/1=
0
Slope is zero
So, since y is always -1 and the slope is zero, the equation will e
y= -1
What is the difference between -12 and -8
Answers
Answer:
-4
Step-by-step explanation:
Annie's squirt gun holds two tanks one tank holds 968 ML and the other tank holds 784 ML how many liters does the squirt gun hold in total
Answers
ayo
968ml + 784ml = 1752ml or 1.752Liter
what two number multiply to -8 but add up to -7
Answers
Answer:
-8 and 1
Step-by-step explanation:
\(-8*1=-8\\\\-8+1=-7\)
the apothem is the perpendicular distance from the _____ of a regular polygon to any one of its sides.
Answers
The apothem is the perpendicular distance from the center of a regular polygon to any one of its sides.
A closed, two-dimensional, flat or planar structure with straight sides is referred to as a polygon. Its sides do not bend in any way. A polygon's sides are also referred to as its edges. A polygon's vertices (or corners) are the places where two sides converge. Polygons and polyhedrons are two names for geometric shapes having three or more sides. The names of a few polygons are listed below. In order to link and develop projects and blockchains that are compatible with Ethereum, Polygon (MATIC), a cryptocurrency and technological platform, was introduced. A fully closed polygon is a flat, two-dimensional form with straight sides. They must have straight sides. Any number of sides can be found in polygons.
To know more about polygon here
https://brainly.com/question/1592456
#SPJ4
HELP!!!!! I DONT KNOW THIS

Answers
Answer:
neither
Step-by-step explanation:
exponential grows larger with each step and liner is constant
Answer:
Exponential because you don't start at 0
Step-by-step explanation:
Find (dy)/(dt) for each pair of function: y=x^(2)-6x,x=t^(2)+4 (dy)/(dt)
Answers
The derivative (dy)/(dt) for the given pair of functions is (dy)/(dt) = 2t - 6. To find (dy)/(dt), we need to differentiate the function y with respect to t.
Let's start with the given functions:
1. y = x^2 - 6x
2. x = t^2 + 4
First, let's find dx/dt by differentiating the second function with respect to t:
dx/dt = d/dt(t^2 + 4)
= 2t
Now, we can find (dy)/(dt) by substituting the value of dx/dt into the derivative of y:
(dy)/(dt) = d/dt(x^2 - 6x)
= d/dt((t^2 + 4)^2 - 6(t^2 + 4)) [Substituting x = t^2 + 4]
= d/dt(t^4 + 8t^2 + 16 - 6t^2 - 24)
= d/dt(t^4 + 2t^2 - 8)
= 4t^3 + 4t
Therefore, the derivative (dy)/(dt) for the given pair of functions is (dy)/(dt) = 2t - 6.
To find the derivative (dy)/(dt), we first differentiate the function y = x^2 - 6x with respect to x, using the power rule of differentiation. The derivative of x^2 is 2x, and the derivative of -6x is -6.
Next, we need to find dx/dt by differentiating the function x = t^2 + 4 with respect to t. The derivative of t^2 is 2t, and the derivative of 4 is 0 (since it is a constant).
To find (dy)/(dt), we substitute the values of dx/dt and dy/dx into the chain rule of differentiation, which states that (dy)/(dt) = (dy)/(dx) * (dx)/(dt).
In this case, (dy)/(dx) is 2x - 6 and (dx)/(dt) is 2t. Therefore, we have (dy)/(dt) = (2x - 6) * (2t) = 4xt - 12t.
Since x = t^2 + 4, we substitute this value into the expression to get (dy)/(dt) = 4(t^2 + 4)t - 12t = 4t^3 + 16t - 12t = 4t^3 + 4t.
Hence, (dy)/(dt) for the given pair of functions is (dy)/(dt) = 2t - 6.
To learn more about function, click here: brainly.com/question/11624077
#SPJ11
What is the solution to this system of equations?
4x + 5y = 7
3x - 2y = -12
Multiply each equation by a number that produces opposite
coefficients for x ory:
45
The solution is
BN
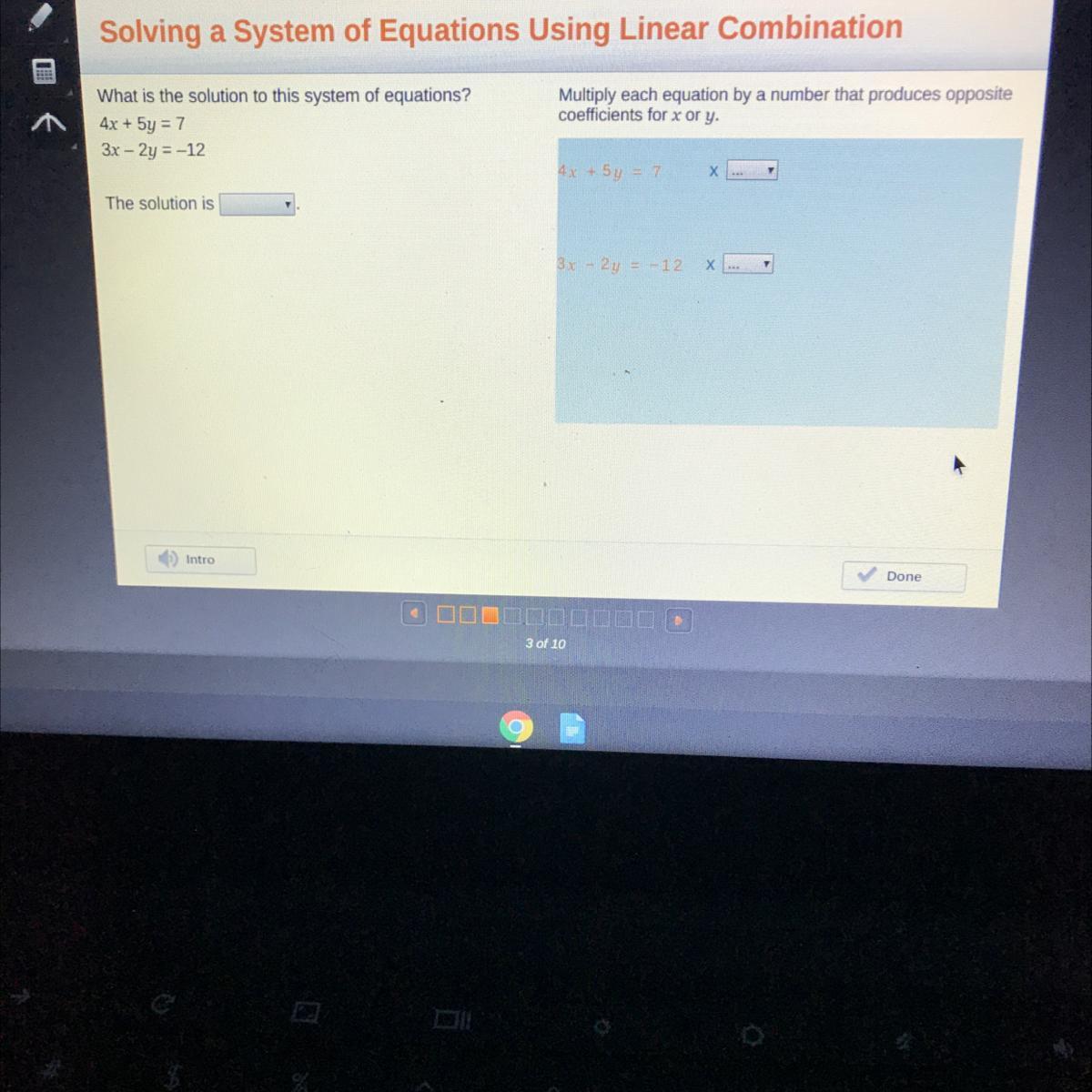
Answers
Answer:
x = -2, y = 3
Step-by-step explanation:
Given equations are,
4x + 5y = 7 ---------(1)
3x - 2y = -12 ----------(2)
Multiply equation (1) by 3
12x + 15y = 21 ------(3)
Multiply equation (2) by (-4)
-12x + 8y = 48 --------(4)
Now add equations (3) and (4),
(12x + 15y) + (-12x + 8y) = 21 + 48
(12x - 12x) + (15y + 8y) = 69
23y = 69
y = 3
From equation (2),
3x - 2(3) = -12
3x - 6 = -12
3x = 6 - 12
x = -2
Therefore, x = -2 and y = 3 will be the answer.
Answer:
What is the solution to this system of equations?
\(4x +5y = 7\)
\(3x-2y=-12\)
The solution is ✔ \((-2,3)\) .
It is a straight path that goes on without end in two directions. What is it?
A. line
B. plane
C.ray
D. triangle
Answers
The correct answer is A. line. A line is a straight path that extends infinitely in both directions. It has no endpoints and continues indefinitely.
A line is a basic geometric object that is defined by two points or can be represented by a single equation. It is characterized by its straightness and infinite length, extending in both directions without any boundaries or endpoints. A line can be represented by a straight line segment with two distinct points or by an equation such as y = mx + b in a coordinate system.
On the other hand, a plane refers to a two-dimensional flat surface that extends infinitely in all directions. It is not a straight path but rather a flat, continuous surface. A ray, is a part of a line that has one endpoint and extends infinitely in one direction. It is not a straight path that continues indefinitely in both directions like a line.
A triangle is a closed geometric shape with three sides and three angles. It is not a straight path but rather a closed figure formed by connecting three non-collinear points.Therefore ,the correct answer is A.
learn more about straight line :
https://brainly.com/question/31693341
#SPJ4
Please help me find X and Y.
2x - 4y = 36
4x + 3y = -5
A: (-7, 4)
B: (7, -4)
C: (-4, 7)
D: (4, -7)
Answers
Answer: B: (7, -4)
Step-by-step explanation:
To solve for x and y, we can use either substitution or elimination method. Here, we'll use the elimination method to solve for x and y:
2x - 4y = 36 (Equation 1)
4x + 3y = -5 (Equation 2)
To eliminate y, we can multiply Equation 1 by 3 and Equation 2 by 2, and then add the two resulting equations:
6(2x - 4y) = 6(36) (Multiplying Equation 1 by 3)
2(4x + 3y) = 2(-5) (Multiplying Equation 2 by 2)
Simplifying, we get:
12x - 24y = 216
8x + 6y = -10
Adding the two equations, we get:
20x = 206
Dividing both sides by 20, we get:
x = 10.3
Now, substituting x = 10.3 into Equation 1 or Equation 2, we can solve for y. Let's use Equation 1:
2x - 4y = 36
2(10.3) - 4y = 36
20.6 - 4y = 36
-4y = 15.4
y = -3.85
Therefore, the solution to the system of equations is (x,y) = (10.3,-3.85).
Rounded to the nearest integer, the solution is approximately (x,y) = (10,-4).
So, the answer is option B: (7, -4).
Answer:
D. (4, 7)
Step-by-step explanation:
2x - 4y = 36
4x + 3y = -5
2(4) - 4(-7) = 36
4(4) + 3(-7) = -5
the solid with a semicircular base of radius whose cross sections perpendicular to the base and parallel to the diameter are squares
Answers
The solid with a semicircular base of radius "r" and cross sections perpendicular to the base and parallel to the diameter are squares is called a "right circular cylinder with a half-circle base".
The height of the cylinder is equal to the side length of the square cross sections, and the radius of the semicircular base is equal to "r". The volume of this solid can be calculated as follows:
V = (Pi * r^2 * h) / 2
where Pi is the mathematical constant pi (approx. equal to 3.14), r is the radius of the semicircular base, h is the height of the cylinder, and "/ 2" represents that the volume is half of a full cylinder with a complete circular base.
To know more about Square:
https://brainly.com/question/28776767
#SPJ4
Three cars are shown below, along with
their original prices.
The price of each car is then rounded to
the nearest £100.
a) Work out which car's price changes the
most.
b) By how much does this car's price
change?
Car X
£18,920
MATHS X
Car Y
£12,490
MATHS Y
Car Z
£16,340
MATHS Z

Answers
Step-by-step explanation:
a.) First, we need to take each car's price and round it.
Car X: £18,920
Rounded to the nearest £100: £18,900
Car Y: £12,490
Rounded to the nearest £100: £12,500
Car Z: £16,340
Rounded to the nearest £100: £16,300
Now, we need to figure out how much each car's price changes. To do this, we will take the car's original price and subtract the rounded price.
Car X:
£18,920 - £18,900 = £20
The car's price changed by £20.
Car Y:
£12,490 - £12,500 = -£10
The car's price changed by £10.
Car Z:
£16,340 - £16,300 = £40
The car's price changed by £40.
So, car Z had the largest price change of £40.
b.) Use the information already gathered from above
Car X: The car's price changed by £20.
Car Y: The car's price changed by £10.
Car Z: The car's price changed by £40.
If this helped you, please leave a thanks or a Brainliest!!!
Hope you have a GREAT day!!!
Suppose the function f(x) = x2 − 6x + 12 describes a physical situation that makes sense only for whole numbers between 0 and 20 (such as family expense as a function of the number of children). For what value of x does f reach a minimum, and what is the minimum value? (Suggestion: We suggest a table starting at 0 with a table increment of 1. )
x-value
Answers
The function f(x) = x^2 − 6x + 12 can be written in the form f(x) = (x - 3)² + 3. This means that the function has a minimum value of 3 when x = 3.
To find the minimum value of the function, we can take the derivative of the function and set it equal to 0.
f'(x) = 2x - 6 = 0
Solving for x, we get x = 3.
Substituting this value back into the original function, we get:
f(3) = (3)² - 6(3) + 12 = 3
So the minimum value of the function is 3 when x = 3.
In conclusion, the function f(x) = x² − 6x + 12 reaches a minimum value of 3 when x = 3.
Learn more about optimum value here:
https://brainly.com/question/16573288
#SPJ11
Points D and E are midpoints of the sides of triangle ABC. The perimeter or the triangle is 48 units. What is the value of t?
Answers
Answer:
2 units
Step-by-step explanation:
A triangle is a polygon with three sides and three angles. Types of triangle are acute, obtuse, scalene, isosceles, equilateral and right angled triangle.
Since point D and E are midpoints of the sides of triangle ABC, hence:
AD = BD = 3t, BE = CE = 4t, AC = 7t + 6
The perimeter of triangle ABC = AC + BC + AB = AC + AD + BD + BE + CE;
Substituting:
48 = 7t + 6 + 3t + 3t + 4t + 4t = 21t + 6
48 = 21t + 6
21t = 42
t = 2 units
