Answers
Answer:
i think it is the 4th one
Step-by-step explanation:
yo it would be cool if you would give me brainliest
Related Questions
Please help I have 11 more to solve.

Answers
Which statement is true?

Answers
Answer:
(b) Both vertical and horizontal reflection
Step-by-step explanation:
The figure will be a horizontal reflection of itself about any vertical line through two of the smaller 6-pointed stars.
The figure will be a vertical reflection of itself about any horizontal line through two of the smaller 6-pointed stars.
the pattern has both vertical and horizontal reflection
__
Additional comment
A pattern will have horizontal reflection if there exists a vertical line about which the pattern can be reflected to itself. That is, there exists one (or more) vertical lines of symmetry.
Similarly, the pattern will have vertical reflection if there is a horizontal line about which the pattern can be reflected to itself. Such a line is a horizontal line of symmetry.
If you had money in a savings account earning 9% interest per year, how much would you make in interest on a deposit of $60.00 over two years?
Answers
The amount of interest earned on a deposit of $60.00 at a rate of 9% per annum for 2 years is $108.
As per the given problem:
Amount deposited = $60.00
Interest rate per year = 9%
The formula for calculating the interest is given by:
Interest = (Principal × Rate × Time)/100
Where Principal is the initial amount invested or deposited
Rate is the percentage of interest that you earn per annum
Time is the duration for which you want to calculate the interest
Putting the values in the above formula, we get:
Interest = (60 × 9 × 2)/100= (108 × 1)/1= $108
So, the amount of interest earned on a deposit of $60.00 at a rate of 9% per annum for 2 years is $108.
for such more question on interest
https://brainly.com/question/25845758
#SPJ11
Given parallelogram L M N O below, LP = 81 If PN = -7x-3 solve for x

Answers
-7x=81+3
-7x/7=84/-7
Solution
X=-12
Answer:-12x
Step-by-step explanation:
just trust me on this
Find the area brainliest if correct no links
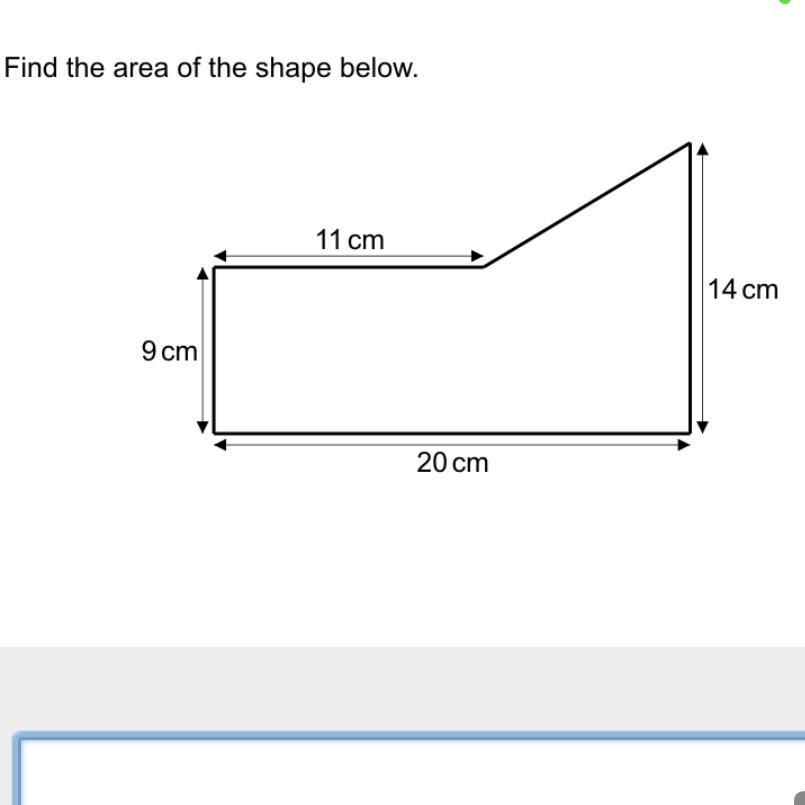
Answers
Answer:
27720
Hope its right :)
Step-by-step explanation:
Answer:
202.5
Step-by-step explanation:
Start by finding the area of the triangle part using the lengths of 9 , 9 , and 5
That gives you 22.5
Then find the area of the rectangle part using the sides of 20 and 9
This gives you 180
When you add them you get 202.5
I hope that this helps!!
A ball is thrown downward from the top of a 140 -foot building with an initial velocity of 24 feet per second. The height of the ball h in feet after t seconds is given by the equation h=-16t^(2)-24t+140.
Answers
In a case whereby a ball is thrown downward from the top of a 140-foot building with an initial velocity of 16 feet per second. the time the ball is thrown will it strike the ground at t = 2.5 or -3.5.
How can the time be calculated?Height of building = 140 ft
Initial velocity, u = 16 ft/sec
the equation given is
h = -16t² -16t +140
h(t) = -16t² -16t +140
AT h(t) = 0 , We can divide by -2 and have
(8t² + 8t - 70) = 0
8t² + 8t - 70 = 0
Then if we solve with quadratic equation formula where a=8, b=8, c=- 70 then the root will be -7/2 and 5/2 then t = 2.5 or -3.5
Learn more about height at:
https://brainly.com/question/10460287
#SPJ1
complete question;
A ball is thrown downward from the top of a 140-foot building with an initial velocity of 16 feet per second. the height of the ball h in feet after t seconds is given by the equation h equals negative 16 t squared minus 16 t plus 140. how long after the ball is thrown will it strike the ground?
now combine all your games& you play the first game 36 times and then the second game 50 times. what is the probability of losing less than $72 in total?
Answers
The probability of losing less than $72 in total is 0.68.
To find the probability of losing less than $72 in total, we need to first calculate the expected loss for each game and then use the law of total probability to find the overall probability.
First, let's calculate the expected loss for each game. The expected loss for the first game is 36 * -2 = -72, and the expected loss for the second game is 50 * -1.5 = -75.
Now, we need to use the law of total probability to find the overall probability of losing less than $72 in total. The law of total probability states that the probability of an event occurring is the sum of the probabilities of the event occurring under each possible condition. In this case, the possible conditions are losing less than $72 in the first game and losing less than $72 in the second game.
So the overall probability of losing less than $72 in total is:
P(losing less than $72) = P(losing less than $72 in first game) + P(losing less than $72 in second game) - P(losing less than $72 in both games)
= (36/100) + (50/100) - (36/100) * (50/100)
= 0.36 + 0.5 - 0.18
= 0.68
Know more about probability here:
https://brainly.com/question/13604758
#SPJ11
let ()=31/4(3−7). f(x)=3x1/4(x3−7). evaluate the following specific values of ′f′: (a) ′(1)f′(1) = (b) ′(4)f′(4) =
Answers
To evaluate the specific values of the derivative of the function f(x) = 3x^(1/4)(x^3 - 7), we need to calculate f'(x) and substitute the given values.
To find the derivative of f(x), we apply the product rule and the power rule of differentiation. The derivative of f(x) is given by:
f'(x) = 3x^(1/4) * d/dx(x^3 - 7) + (x^3 - 7) * d/dx(3x^(1/4))
Using the power rule and the derivative of a constant, we can simplify the expression to:
f'(x) = 3x^(1/4) * (3x^2) + (x^3 - 7) * (3/4)x^(-3/4)
Simplifying further, we have:
f'(x) = 9x^(9/4) + (3/4)(x^3 - 7)x^(-3/4)
Now, we can evaluate the specific values of the derivative:
(a) For x = 1, we substitute x = 1 into f'(x):
f'(1) = 9(1)^(9/4) + (3/4)((1)^3 - 7)(1)^(-3/4)
= 9 + (3/4)(-6)
= 9 - 9/2
= 9/2
Therefore, f'(1) = 9/2.
(b) For x = 4, we substitute x = 4 into f'(x):
f'(4) = 9(4)^(9/4) + (3/4)((4)^3 - 7)(4)^(-3/4)
To evaluate this value, you can plug in the given values and perform the calculations.
Learn more about power rule here:
https://brainly.com/question/30226066
#SPJ11
Use the matrix of transition probabilities P and initial state matrix X_0 to find the state matrices X_1, X_2, and X_3. P = [0.6 0.2 0.1 0.3 0.7 0.1 0.1 0.1 0.8], X_0 = [0.1 0.2 0.7] X_1 = [] X_2 = [] X_1 = []
Answers
To find the state matrices X_1, X_2, and X_3, we can use the transition probability matrix P and the initial state matrix X_0.
P = [0.6 0.2 0.1
0.3 0.7 0.1
0.1 0.1 0.8]
X_0 = [0.1 0.2 0.7]
To calculate X_1, we multiply the transition probability matrix P with the initial state matrix X_0:
X_1 = P * X_0
To calculate X_2, we multiply P with X_1:
X_2 = P * X_1
Similarly, to calculate X_3, we multiply P with X_2:
X_3 = P * X_2
Performing these matrix multiplications will give us the state matrices X_1, X_2, and X_3.
Note: Since the provided matrix P has a dimension of 3x3 and the initial state matrix X_0 has a dimension of 1x3, the resulting state matrices X_1, X_2, and X_3 will also have a dimension of 1x3.
To know more about probabilities click here: brainly.com/question/31828911
#SPJ11
To find the state matrices X₁, X₂, and X₃ given the transition probabilities matrix P and the initial state matrix X₀, we can apply matrix multiplication repeatedly.
P = [0.6 0.2 0.1
0.3 0.7 0.1
0.1 0.1 0.8]
X₀ = [0.1
0.2
0.7]
To find X₁, we multiply P with X₀:
X₁ = P * X₀
To find X₂, we multiply P with X₁:
X₂ = P * X₁ = P * (P * X₀)
To find X₃, we multiply P with X₂:
X₃ = P * X₂ = P * (P * (P * X₀))
Performing the matrix multiplications, we get:
X₁ = [0.6 0.2 0.1] * [0.1
0.2
0.7] = [0.06 + 0.04 + 0.07
0.03 + 0.14 + 0.07
0.01 + 0.02 + 0.56]
X₁ = [0.17
0.24
0.59]
X₂ = [0.6 0.2 0.1] * [0.17
0.24
0.59] = [0.048 + 0.048 + 0.059
0.023 + 0.168 + 0.059
0.007 + 0.048 + 0.472]
X₂ = [0.155
0.25
0.527]
X₃ = [0.6 0.2 0.1] * [0.155
0.25
0.527] = [0.042 + 0.031 + 0.053
0.021 + 0.175 + 0.053
0.006 + 0.05 + 0.422]
X₃ = [0.126
0.249
0.478]
Therefore, the state matrices are:
X₁ = [0.17
0.24
0.59]
X₂ = [0.155
0.25
0.527]
X₃ = [0.126
0.249
0.478]
To know more about state matrix click here: brainly.com/question/30112898
#SPJ11
A simple random sample with n = 56 provided a sample mean of 22.5 and a sample standard deviation of 4.4. (Round your answers to one decimal place.)
a) Develop a 90% confidence interval for the population mean.
b) Develop a 95% confidence interval for the population mean.
c) Develop a 99% confidence interval for the population mean.
Answers
a) The 90% confidence interval for the population mean is approximately (21.52, 23.48).
b) The 95% confidence interval for the population mean is approximately (21.322, 23.678).
c) The 99% confidence interval for the population mean is approximately (20.926, 24.074).
To develop confidence intervals for the population mean, we can use the formula:
Confidence Interval = sample mean ± (critical value * standard error)
where the standard error is equal to the sample standard deviation divided by the square root of the sample size.
a) For a 90% confidence interval, we need to find the critical value corresponding to a confidence level of 90%. The critical value can be obtained from the t-distribution table with (n-1) degrees of freedom. Since the sample size is 56, the degrees of freedom is 56-1 = 55.
From the t-distribution table, the critical value for a 90% confidence interval with 55 degrees of freedom is approximately 1.671.
The standard error can be calculated as:
Standard Error = sample standard deviation / sqrt(sample size)
Standard Error = 4.4 / sqrt(56)
Standard Error ≈ 0.5882
Now we can calculate the confidence interval:
Confidence Interval = 22.5 ± (1.671 * 0.5882)
Confidence Interval = 22.5 ± 0.9816
Confidence Interval ≈ (21.52, 23.48)
b) For a 95% confidence interval, the critical value for 55 degrees of freedom is approximately 2.004 (obtained from the t-distribution table).
Standard Error = 4.4 / sqrt(56) ≈ 0.5882
Confidence Interval = 22.5 ± (2.004 * 0.5882)
Confidence Interval = 22.5 ± 1.178
Confidence Interval ≈ (21.322, 23.678)
c) For a 99% confidence interval, the critical value for 55 degrees of freedom is approximately 2.678 (obtained from the t-distribution table).
Standard Error = 4.4 / sqrt(56) ≈ 0.5882
Confidence Interval = 22.5 ± (2.678 * 0.5882)
Confidence Interval = 22.5 ± 1.574
Confidence Interval ≈ (20.926, 24.074)
For more such question on mean visit:
https://brainly.com/question/1136789
#SPJ8
I need help y’all pls I will give brainliest

Answers
Answer: (-2,-2)
Step-by-step explanation:
Start at finding the y-intercept(-3) then do rise over run with -2x
Rise over run is count up/down then left/right
polynomial F(x) is divided by x and (x+1), we get remainder 0 and 1 respectively. Find the value of R(2) if R(x) is the remainder when F(x) is divided by x(x +1).
Answers
Answer:
Hello,
R(2)=-2
Step-by-step explanation:
\(F(x)=q_1(x)*x+0 \ , \ F(0)=0 \\F(x)=q_2(x)*(x+1)+1\ , \ F(-1)=1\\\\F(x)=q_3*x*(x+1)+(a*x+b)\\\\if\ x=0\ then\ F(0)=0=a*0+b \Longrightarrow\ b=0\\\\if\ x=-1\ then\ F(-1)=1=a*(-1)+b \Longrightarrow\ a=-1\\\\\\R(x)=ax+b=-x\\R(2)=-2\\\)
The perimeter of the figure below is 40 cm. what is the length of the side labelled ‘x’?

Answers
Answer:
13.72 cm
Step-by-step explanation:
Perimeter of the given figure = sum of all sides
40 = x + 9.7 + 16.58
40 = x + 26.28
x = 40 - 26.28
x = 13.72 cm
In triangle rst, m∠r > m∠s m∠t. which must be true of triangle rst? check all that apply. m∠r > 90° m∠s m∠t < 90° m∠s = m∠t m∠r > m∠t m∠r > m∠s m∠s > m∠t
Answers
Only two options are necessarily true for the triangle,
m∠r > 90°
m∠s + m∠t < 90°
In any triangle, the sum of the three angles is 180 degrees. If m∠r > m∠s + m∠t, then angle r must be the largest angle in the triangle. Additionally, the sum of the other two angles (s and t) must be less than 90 degrees.
Option m∠s = m∠t is not necessarily true because the two angles could be different and still add up to be less than m∠r. Options m∠r > m∠t, m∠r > m∠s, and m∠s > m∠t are not necessarily true and depend on the specific values of the angles in triangle RST.
To know more triangle, here
brainly.com/question/31315456
#SPJ4
A school gymnasium can hold 256 people for an awards banquet. There will be 10 staff members in attendance.
The principal is trying to determine how many guests each award recipient can invite if each invites the same?
number of people (p). There are 41 award recipients. The principal's calculations are shown.
41p + 10 < 256
41p 246
p 26
Are the principal's calculations correct, and why?
Answers
A school gymnasium can hold 256 people for an awards banquet. There will be 10 staff members in attendance. The principal is trying to determine how many guests each award recipient can invite if each invites the same number of people (p).
There are 41 award recipients. The principal's calculations are shown as follows:41p + 10 < 256 41p < 256 - 10 = 246 p < 246/41 p < 6, so p = 5Award recipients are able to invite more than 100 guests if the number of award recipients is less than or equal to 20. Since there are 41 award recipients, each can invite no more than 5 guests. The total number of guests that can be accommodated is:41(5) + 10 = 205 + 10 = 215Therefore, the calculations made by the principal are correct.
To know more about award visit:
https://brainly.com/question/31928643
#SPJ11
Please Help me - You will get 60 points for the rapid reply- Use isosceles trapezoid ABCD to determine the following measurements-

Answers
Answer:
1) AD = 9 in
2) DE = 9.25 in
3) ∠EDC = 36°
4) ∠AEB = 108°
5) 11.5 in
Step-by-step explanation:
1) AD = BC = 9in
2) AC = BD (diagonals are equal)
⇒ BD = 14.25
⇒ BE + DE = 14.25
⇒ 5 + DE = 14.25
DE = 9.25
3) Since AB ║CD,
∠ABE = ∠EDC = 36°
4) ∠ABE = ∠BAE = 36°
Also ∠ABE + ∠BAE + ∠AEB = 180 (traingle ABE)
⇒ 36 + 36 + ∠AEB = 180
∠AEB = 108
5) midsegment = (AB + CD)/2
= (8 + 15)/2
11.5
the Bears won 40 games and lost 24 while the Bulls won 32 games and lost eighteen which team has the higher wins?
Answers
Answer:
It looks like the Bears have the higher wins, as they won 40 games while the Bulls won only 32 games.
use a distribute propety for the equiotion 25- (3x+5 ) =2(x +8)+x
Answers
Answer:
x=2/3
Step-by-step explanation:
25-(3x+5)=2(x+8)+x
25-3x-5=2x+16+x
20-3x=3x+16
20-3x-3x=16
20-6x=16
6x=20-16
6x=4x=4/6
simplify
x=2/3
Answer:
x=2/3
Step-by-step explanation:
The sampling distribution of a statistic is
A. the distribution of values taken by a statistic in all possible samples of the same size from the same population.
B. the probability that we obtain the statistic in repeated random samples.
C. the distribution of a particular sample of a certain size.
D. the extent to which the sample results differ systematically from the truth.
E. the mechanism that determines whether randomization was effective.
Answers
Answer:
A
Step-by-step explanation:
the volume of a rectangular pyramid is 512 units 3 3 . if the length of the rectangular base measures 8 units and the width of the rectangular base measures 12 units, find the height of the pyramid.
Answers
The height of the rectangular pyramid is 16 units.
To find the height of the rectangular pyramid, we can use the formula for the volume of a pyramid:
Volume = (1/3) * base area * height
Given that the volume of the rectangular pyramid is 512 units^3, and the length of the rectangular base is 8 units and the width is 12 units, we can find the base area:
Base Area = length * width = 8 * 12 = 96 units^2
Now we can substitute the values into the volume formula:
512 = (1/3) * 96 * height
To solve for the height, we can isolate it by multiplying both sides of the equation by 3/96:
512 * 3/96 = height
Simplifying the right side of the equation:
16 = height
The rectangular pyramid is 16 units tall as a result.
for such more question on height
https://brainly.com/question/16269079
#SPJ8
PLEASE HELP ASAP ITS URGENT

Answers
Step-by-step explanation:
the answer is in the image above

jax bought exactly enough trees to plant eight equal rows. then one tree died and couldn't be planted, but he still had enough trees left to plant exactly nine equal rows. after that, a tree was stolen, but he still had enough trees left to plant exactly ten equal rows. if he bought the least number of trees satisfying these three conditions, how many trees did he buy?
Answers
Jax bought 92 trees to satisfy these three conditions.
To find the number of trees Jax bought, we can start by setting up a system of equations based on the given conditions:
Let's say the number of trees Jax bought is 'x'.
Condition 1: Jax had enough trees to plant 8 equal rows and one tree died.
So, the number of trees after one tree died is (x - 1).
Condition 2: Jax had enough trees to plant 9 equal rows after one tree died.
Therefore, (x - 1) should be divisible by 9.
Condition 3: Jax had enough trees to plant 10 equal rows after one tree died and another tree was stolen.
So, the number of trees after two trees were lost is (x - 2).
Therefore, (x - 2) should be divisible by 10.
By solving these equations simultaneously, we can find the value of 'x'.
(x - 1) should be divisible by 9, and (x - 2) should be divisible by 10. The least common multiple of 9 and 10 is 90.
So, (x - 2) should be equal to 90.
Therefore, x - 2 = 90
Simplifying the equation, we get:
x = 92
Hence, Jax bought 92 trees to satisfy these three conditions.
By finding the least common multiple of 9 and 10, which is 90, we can set up the equation (x - 2) = 90.
Solving for x, we get x = 92. Therefore, Jax bought 92 trees to satisfy all three conditions.
To know more about least common multiple visit:
https://brainly.com/question/379419
#SPJ11
Which of the following shapes is
considered to be a 2 dimensional
figure?
A. A cylinder
B. A cube
C. A pyramid
D. A circle

Answers
Answer:
D, Circle
Step-by-step explanation:
All the other shapes are 3D and have a volume.
6+a/2 = 28
solve for a please help :)
Answers
Answer:
The correct answer is a = 44.
Step-by-step explanation:
To solve this problem, we need to isolate the variable (a) on one side of the equation. Our first step should be to subtract 6 from both sides, which gives us:
6 + a/2 - 6 = 28 - 6
a/2 = 22
Next, we should multiply both sides by 2 to cancel out the fraction on the left side of the equation and get the variable a alone.
a/2 * 2 = 22 * 2
a = 44
Therefore, the answer to your question is a = 44.
For more information about solving equations, check out the following questions:
https://brainly.com/question/13482978
https://brainly.com/question/28224805
Evaluate the line integral, where C is the given space curve. C xeyz ds, C is the line segment from (0, 0, 0) to (4, 3, 2)
Answers
We integrate each component separately over the given limits of t. Evaluating the integral for each component will yield the final result of the line integral of F along the line segment C from (0, 0, 0) to (4, 3, 2).
A line integral is a way to calculate the work done by a force along a curve. In this case, we have the vector field F = xeyz and the curve C, which is the line segment from (0, 0, 0) to (4, 3, 2). The line integral of F along C can be written as ∫CF · dr, where dr is the differential vector along the curve.
To evaluate this line integral, we parameterize the curve C. Since C is a line segment, we can use a linear parameterization. Let's denote the parameter as t, ranging from 0 to 1. We can express the coordinates of C as x = 4t, y = 3t, and z = 2t.
Next, we need to find the differential vector dr along curve C. Taking the derivatives of the parameterized equations with respect to t, we obtain dx = 4dt, dy = 3dt, and dz = 2dt. Hence, dr = (dx, dy, dz) = (4dt, 3dt, 2dt).
Substituting these values into the line integral, we have ∫CF · dr = ∫CF(x, y, z) · (4dt, 3dt, 2dt). Simplifying the expression, we get ∫C(4xeyz dt, 3xeyz dt, 2xeyz dt).
Learn more about limits here:
https://brainly.com/question/12207539
#SPJ11
What would be the solution to the system of equations: y= -x + 4 y= 3x
Answers
Answer:
Step-by-step explanation:
The value of y is given in equation 2
Putting value of y = 3x in equation 1
Y = - x + 4
3x = - x + 4
Bringing like terms on one side
3x + x = 4
4x = 4
x = 4/4 = 1
Now putting value of x = 1 in equation 2
Y = 3x
Y = 3(1) = 3
A paddleboat can move at a speed of 14 kilometers per hour in still water. The boat is paddled 10 kilometers downstream in a river in the same time it takes to go 5 kilometers upstream. What is the speed of the river? Round your answer to the nearest tenth.
Answers
The speed of the river is 7.5 kilometers per hour.
Let the speed of boat in still water = u = 14 km/h
Let the speed of river = v = x km/h
Upstream speed = u - v = 14 - x
Downstream speed = u + v = 14 +x
Distance paddled upstream = \(D_{1}\) = 5 km
Distance paddled downstream = \(D_{2}\) = 10 km
Time taken (upstream) = \(T_{1}\) = \(\frac{D_{1} }{u-v}\)
Time taken (downstream) = \(T_{2}\) = \(\frac{D_{2} }{u+v}\)
According to question,
\(T_{1}\) = \(T_{2}\)
\(\frac{D_{1} }{u-v}\) = \(\frac{D_{2} }{u+v}\)
\(\frac{5}{14-x}\) = \(\frac{10}{14+x}\)
5(14 + x) = 10(14 - x)
14 + x = 2(14 - x)
14 + x = 28 - 2x
x + 2x = 28 - 14
3x = 14
x = \(\frac{14}{3}\)
x = 7.5
Hence, Speed of river is 7.5 km/h.
Learn more about speed on:
https://brainly.com/question/7359669
#SPJ1
Can anyone help me with this?

Answers
\(Draw\ \overline {AB}\perp\overline {CD}\ at\ point \ A.\)

Consider the following table summarizing the speed limit of a certain road and the number of accidents occurring on that road in January.
Posted Speed Limit
51
47
41
38
21
20
Reported Number of Accidents
27
26
21
16
17
11
1) Find the slope of the regression line predicting the number of accidents from the posted speed limit. Round to 3 decimal places.
2) Find the intercept of the regression line predicting the number of accidents from the posted speed limit. Round to 3 decimal places.
3) Predict the number of reported accidents for a posted speed limit of 10mph. Round to the nearest whole number.
Answers
The answers are as follows 1. The slope of the regression line predicting the number of accidents from the posted speed limit is -0.510 (approx). 2. The y-intercept of the regression line predicting the number of accidents from the posted speed limit is 150.43 (approx). 3. The predicted number of reported accidents for a posted speed limit of 10 mph is 145.
1. The slope of the regression line predicting the number of accidents from the posted speed limit: Given, Posted Speed Limit: 51, 47, 41, 38, 21, 20Reported Number of Accidents: 27, 26, 21, 16, 17, 11
The scatter plot for the given data is: The equation of the regression line is y = ax + b, where y is the dependent variable, x is the independent variable, a is the slope of the line, and b is the y-intercept of the line.
Therefore, Slope (a) of the regression line can be found by: Slope (a) = [n(∑xy) - (∑x)(∑y)] / [n(∑x²) - (∑x)²]Here, n is the number of data points∑x = 218, ∑y = 118∑xy = 4448, ∑x² = 9950n = 6. Therefore, slope of the regression line is: Slope (a) = [6(4448) - (218)(118)] / [6(9950) - (218)²] = -0.510 (approx)
Hence, the slope of the regression line predicting the number of accidents from the posted speed limit is -0.510 (approx).
2. The intercept of the regression line predicting the number of accidents from the posted speed limit: The slope of the regression line has already been found in the above question.
Now, we can find the y-intercept of the regression line by using the slope (a) and the following formula: y-intercept (b) = (∑y - a(∑x)) / n. Here, n is the number of data points∑x = 218, ∑y = 118a = -0.510
Therefore, the y-intercept of the regression line predicting the number of accidents from the posted speed limit is: y-intercept (b) = (118 - (-0.510)(218)) / 6= 150.43 (approx)
Hence, the y-intercept of the regression line predicting the number of accidents from the posted speed limit is 150.43 (approx).
3. Predict the number of reported accidents for a posted speed limit of 10mph: Using the equation of the regression line:y = ax + by = -0.510x + 150.43Putting x = 10, we get:y = -0.510(10) + 150.43= 145.4 (approx)
Rounding to the nearest whole number, the predicted number of reported accidents for a posted speed limit of 10 mph is 145.
For more questions on: slope of the regression
https://brainly.com/question/32610808
#SPJ8
(a^2 + b^2)^2 + (a^8 + b^8)^2
Answers
Answer:
a^4+2ab^2+b^4+a^16+2ab^8+b^16
Step-by-step explanation:
(a^2+b^2)^2+(a^8+b^8)^2
(a^2+b^2)^2=(a^2+b^2)(a^2+b^2)
=a^2(a^2+b^2)+b^2(a^2+b^2)
=a^4+(ab)^2+(ba)^2+b^4
=a^4+2ab^2+b^4
(a^8+b^8)^2=(a^8+b^8)(a^8+b^8)
=a^8(a^8+b^8)+b^8(a^8+b^8)
=a^16+(ab)^8+(ba)^8+b^16
=a^16+2ab^8+b^16
(a^2+b^2)^2+(a^8+b^8)^2=(a^4+2ab^2+b^4)+(a^16+2ab^8+b^16)
the answer is a^4+2ab^2+b^4+a^16+2ab^8+b^16
i think it is simplified answer
