please help step by step -8n +3 +n + 11
Answers
Answer: −8n+3+n+11
Add the terms
−7n+3+11
Solution
−7n+14
Step-by-step explanation: hope this helps
Add the terms
-7n+3+11
-7n+14
Related Questions
Which expression gives the distance between the points (5, 1) and (9,-6)? O A. (5-9)2 + (1+6)2 O B. 15 - 9)2 + (1 - 6)? O C. /15 - 9)2 + (1 +6) OD. (5-9)2 + (1 - 6)?

Answers
Answer:
C.
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
BracketsParenthesisExponentsMultiplicationDivisionAdditionSubtractionLeft to RightAlgebra II
Distance Formula: \(\displaystyle d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)Step-by-step explanation:
Step 1: Define
Point (5, 1)
Point (9, -6)
Step 2: Identify
x₁ = 5, x₂ = 9
y₁ = 1, y₂ = -6
Step 3: Find distance d
Simply plug in the 2 coordinates into the distance formula to find distance d
Substitute in points [DF]: \(\displaystyle d = \sqrt{(5-9)^2+(1+6)^2}\)Here,
two points are (5,1) and (9,-6)
So,
x1=5
x2=9
y1=1
y2= -6
we know that,
Distance formula:- \(\bold{D=\sqrt{(x_2 - x_1 )^2+(y_2 - y_1)^2} }\)
According to the question,
Distance between (5,1) and (9,-6)
\(\bold{D=\sqrt{(5-9)^2+(1-\{-6\})^2} }\)
\(\bold{D=\sqrt{(5-9 )^2+(1+6)^2} }\)
so,
option C is correct..
Find the probability of getting a black card and 3?

Answers
SOLUTION:
Case: Probability (Deck of cards)
A standard 52-card deck comprises 13 ranks in each of the four French suits: clubs (♣), diamonds (♦), hearts (♥) and spades (♠). Each suit includes three court cards (face cards), King, Queen and Jack, with reversible (double-headed) images. Each suit also includes ten numeral cards or pip cards, from one to ten. The card with one pip is known as an Ace. Each pip card displays the number of pips (symbols of the suit) corresponding to its number, as well as the appropriate numeral (but "A" for the Ace) in at least two corners.
Given:
A deck of cards
Required: To find the probability of obtaining a card that is has the number 3 and is black
Method:
Step 1: First, the total number of cards in a deck is 52
Step 2: The total obtainable black number 3 cards are:
3 clubs and 3 spades. This is a total of 2 outcomes
Step 3: The probability of getting a the number 3 and is black is:
\(\begin{gathered} Pr(3B)\text{ =}\frac{2}{52} \\ Pr(3B)=\text{ }\frac{1}{26} \end{gathered}\)Final answer:
The probability is 1/26
Find a polynomial function of degree 3 such that f(0)=17 and the square root of f(x) are 0,5 and 8
Answers
Answer:
f(x)=x^3 - 13x^2 + 40x + 17
Step-by-step explanation:
x-0=0 x-5=0 x-8=0
x=0 x=5 x=8
y=x(x-5)(x-8)+b ==> b is what's going to be used to find the equation so that
y=17 when x=0
17=0(0-5)(0-8)+b ==> plugin 0 for x and 17 for y
17=0*(-5)*(-8)+b ==> simplify
17=0+b ==> anything multiplied by 0 is 0.
b=17
Hence, the equation is:
y=x(x-5)(x-8)+17 ==> expand this equation
y=x*(x-5)(x-8) + 17
y=x*(x(x - 8) - 5(x - 8)) + 17 ==> distribute x-8 to x and -5
y=x*(x*x - 8x - 5x - (8)(-5)) + 17 ==> distribution property
y=x*(x^2 - 13x - (-40)) + 17 ==> simplify
y=x*(x^2 - 13x + 40) + 17 ==> subtracting a negative number is equivalent to
adding a positive number
y=x^3 - 13x^2 + 40x + 17 ==> multiply x with x^2, 13x, and 40 using the
distribution property.
Answer: f(x)=x^3 - 13x^2 + 40x + 17
Answer: Okay, lets explain.
Step-by-step explanation:Since 0, 5 & 8 are given as the zeros of the required 3rd degree polynomial f(x), therefore, one may take it as ; f(x) =k (x-0)(x-5)(x-8)
= k(x³−13x²+40) …. .. .(1) . Since f(10) = 17 (given), it implies 17 = k(1000 -1300 + 400) = 100 ==> k = 17/100 = 0.17 . Put this value of k in eq(1) and get the required polynomial.
50 in.
14 in.
Find the length of the missing side.
52 in.
24 in.
48 in.
16 in.
Answers
Answer:
48
Step-by-step explanation:
Find the y-intercept and the slope of the line.
5x+4y=-3
Write your answers in simplest form.
y-intercept:
Slope:
No choices solve on own
Answers
Answer:
y - intercept: 3/4
slope: -5/4
Step-by-step explanation:
put into slope-intercept form first, y = -5/4x + 3/4
then you can see that the slope and y - intercept are -5/4 and 3/4
Answer:
The answer for the y-intercept is (0, -3/4). The answer for the slope is -5/4.
Step-by-step explanation:
You know this because you must pull the 4 out of the equation, along with the y, so it is -4y=5x+3. You would put both of these numbers over 4: (5 and 3). A positive number which is 5, divided by a negative gives you negative so you can just say -5/4. Same with +3/-4. You can change it to -3/4, because positive over negative equals negative answer.
(co 6) a data set whose original x values ranged from 28 through 49 was used to generate a regression equation of ŷ = 2.9x – 34.7. use the regression equation to predict the value of y when x=44.
Answers
The coefficient of determination or R² is a statistic that measures the correlation between a regression line and a set of points. It represents how much of the variation in the dependent variable is explained by the independent variable in a linear regression model.
It's a number between 0 and 1, and the closer it is to 1, the better the model fits the data. To calculate R², the formula is:
R² = 1 - (SSres/SStot),
where SSres is the sum of squared residuals (the difference between the predicted and actual values) and SStot is the total sum of squares (the difference between each value and the mean).
In the given problem, we have a regression equation of ŷ = 2.9x – 34.7, which means that the predicted value of y (or ŷ) is equal to 2.9 times x minus 34.7.
To predict the value of y when x = 44, we can substitute the value of x into the equation and solve for ŷ:
ŷ = 2.9(44) - 34.7ŷ = 127.3
Therefore, when x = 44, the predicted value of y is 127.3.
To calculate the coefficient of determination, we need to know the sum of squared residuals and the total sum of squares, which we can find using the original data set.
To know more about the Coefficient Of Determination visit:
https://brainly.com/question/31891074
#SPJ11
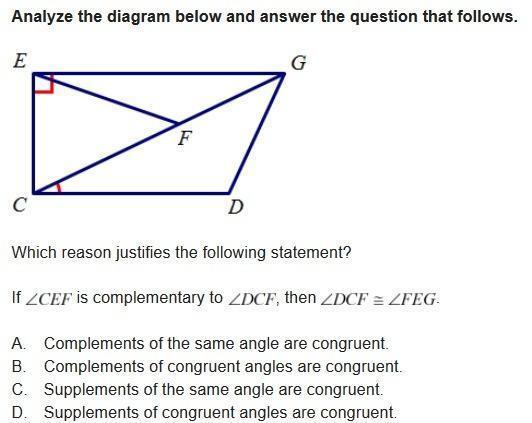
Based on the diagram, which reason justifies this statement?
If ∠CEF is complementary to ∠DCF, then
∠DCF ≅ ∠FEG.
Complements of the same angle are congruent.
Complements of congruent angles are congruent.
Supplements of the same angle are congruent.
Supplements of congruent angles are congruent.
Answers
Answer:
complements of the same angle are congruent
Step-by-step explanation:
edge bro
The correct justification is complements of the same angle are congruent.
What are complementary angles?The angles whose sum is 90° are called complementary angles.
Given that, ∠CEF is complementary to ∠DCF, then ∠DCF ≅ ∠FEG, we need to justify this,
Angles are congruent if they have the same angle measure.
Angles are complementary if their sum = 90°
∠CEF is complementary to ∠DCF
∠CEF + ∠DCF = 90°
While ∠CEF & ∠FEG are also complementary
as ∠CEF + ∠FEG = 90°
∠CEF + ∠DCF = ∠CEF + ∠FEG
∠DCF = ∠FEG
∠DCF ≅ ∠FEG
∠DCF & ∠FEG both are Complements of the ∠CEF
∵ Complements of the same angle are congruent.
Hence, correct justification is complements of the same angle are congruent.
Learn more about complimentary angles, click;
https://brainly.com/question/20693383
#SPJ5
Write the equation of the line (in slope-intercept form) that has an x-intercept at -6 and a y-intercept at 2. Provide a rough sketch of the line indicating the given points. [1 mark]. Exercise 2. For the polynomial f(x) = −3x² + 6x, determine the following: (A) State the degree and leading coefficient and use it to determine the graph's end behavior. [2 marks]. (B) State the zeros. [2 marks]. (C) State the x- and y-intercepts as points [3 marks]. (C) Determine algebraically whether the polynomial is even, odd, or neither.
Answers
To determine if the polynomial is even, odd, or neither, we substitute -x for x in the polynomial and simplify. -3(-x)² + 6(-x) = -3x² - 6x. Since the polynomial is not equal to its negation, it is neither even nor odd.
To write the equation of the line with an x-intercept at -6 and a y-intercept at 2, we can use the slope-intercept form of a line, y = mx + b, where m is the slope and b is the y-intercept.
In this case, the y-intercept is given as 2, so the equation becomes y = mx + 2. To find the slope, we can use the formula (y2 - y1) / (x2 - x1) with the given points (-6, 0) and (0, 2). We find that the slope is 1/3. Thus, the equation of the line is y = (1/3)x + 2.
For the polynomial f(x) = -3x² + 6x, the degree is 2 and the leading coefficient is -3. The end behavior of the graph is determined by the degree and leading coefficient. Since the leading coefficient is negative, the graph will be "downward" or "concave down" as x approaches positive or negative infinity.
To find the zeros, we set the polynomial equal to zero and solve for x. -3x² + 6x = 0. Factoring out x, we get x(-3x + 6) = 0. This gives us two solutions: x = 0 and x = 2.
The x-intercept is the point where the graph intersects the x-axis, and since it occurs when y = 0, we substitute y = 0 into the polynomial and solve for x. -3x² + 6x = 0. Factoring out x, we get x(-3x + 6) = 0. This gives us two x-intercepts: (0, 0) and (2, 0).
To determine if the polynomial is even, odd, or neither, we substitute -x for x in the polynomial and simplify. -3(-x)² + 6(-x) = -3x² - 6x. Since the polynomial is not equal to its negation, it is neither even nor odd.
Learn more about Polynomial here:
brainly.com/question/28973842
#SPJ11
The path of a particular fireworks rocket is modeled by the Find the maximum height of the fireworks rocket. O A. 3 meters O
B. 4.9 meters O
c. 47 meters O
D. 56 meter
Answers
The maximum height of the rocket is 50 meters.
The path of a particular fireworks rocket is modeled by the given equation:
\($$h(t) = -5t^2 + 30t + 5$$\)
where h is the height of the rocket in meters and t is the time in seconds. To find the maximum height of the rocket, we need to find the vertex of the parabola. We can do this by using the formula:-
b/2a for the t-coordinate and then substitute the value of t in the equation to find the corresponding height. The general form of a quadratic function is given as
\($$f(x)=ax^2+bx+c$$\)
where a, b, and c are constants; a ≠ 0.
The vertex of the quadratic function is given as
\($$( -\frac{b}{2a},f(-\frac{b}{2a}))$$\)
Therefore, the formula for the t-coordinate of the vertex of the parabola is:
\($$t = -\frac{b}{2a}$$\)
Here, a = -5 and b = 30. Substituting these values in the above formula, we get:
\($$t = -\frac{30}{2(-5)} = 3$$\)
The corresponding height can be found by substituting t = 3 in the equation for h(t):
\($$h(3) = -5(3)^2 + 30(3) + 5 = 50$$.\)
To learn more about height, visit:
https://brainly.com/question/15047456
#SPJ11
Can a 4 year old count to 100?
Answers
Yes, a 4 year old can typically count to 100.
What is counting?Counting is the process of determining the number of elements in a given set or group of objects. Counting is a basic numerical skill that is used in mathematics and other fields. It involves recognizing patterns and comparing numbers to identify how many items are in a given set. Counting is an important part of early childhood education, as it introduces children to the concepts of number and quantity.
Depending on the child's exposure to numbers, they may be able to count even higher. Counting to 100 is a fundamental skill that can be developed through practice and repetition. Teaching a 5 year old to count to 100 can be done through activities such as counting objects, counting steps, and playing counting games.
To know more about counting click-
https://brainly.com/question/10275154
#SPJ4
I give Brainliest for freeeee and then copy this question and pass the good feeling on
Answers
Answer:
now we made each other happy
Step-by-step explanation:
Answer:
Thanks for freeeeee points
first come first served brainiest

Answers
Answer:
Step-by-step explanation:
2+7+2 seems to be right which is 11
2+7+2 = 11 ft
πd
7π = 21.98
21.98/2 = 10.99
10.99+11 = 21.99 ft
The mistake was that however they may have solved what 7π was, it is a semi-circle so they have forgotten to half 7π
URGENT! WILL MARK BRIANLIEST!!!!

Answers
The caterpillar touches 15 points with two integer coordinates, including the start point (-3, -4) and the end point (25, 38).
What is co-ordinate geometry ?
Coordinate geometry is a branch of mathematics that deals with the study of geometry using the principles of algebra. In coordinate geometry, geometric figures are represented using algebraic equations and analyzed using techniques from algebra and calculus.
The caterpillar moves from (-3, -4) to (25, 38) in a straight line. We can find the equation of the line passing through these two points using the slope-intercept form of the equation of a line:
y - (-4) = (38 - (-4))/(25 - (-3)) * (x - (-3))
y + 4 = 42/28 * (x + 3)
y = 3/2 * x + 19
The caterpillar touches a point with two integer coordinates whenever x and y are both integers. To find these points, we can substitute integer values for x and solve for y. Since the slope of the line is 3/2, every time x increases by 2, y increases by 3.
Starting from x = -3, we can list the integer values of x that the caterpillar touches:
-3, -1, 1, 3, 5, ..., 25
For each value of x, we can compute the corresponding value of y using the equation of the line:
y = 3/2 * x + 1
For example, when x = -3, y = 3/2 * (-3) + 19 = 14.5, which is not an integer. When x = -1, y = 3/2 * (-1) + 19 = 17.5, which is also not an integer. However, when x = 1, y = 3/2 * 1 + 19 = 20, which is an integer. Similarly, we can find the integer values of y for all the other values of x.
Therefore, the caterpillar touches 15 points with two integer coordinates, including the start point (-3, -4) and the end point (25, 38).
To know more about co-ordinate geometry visit:
https://brainly.com/question/18269861
#SPJ1
PLEASE HELP!!!! GIVING BRAINLIEST!!!
Identify the missing input value.

Answers
Answer:
The answers are 34 on the in side and 57 on the out side
Step-by-step explanation:
This is because if you subtract 4 from 9, you will get 5. when you subtract 4 from 19, you will get 15.
I hope this helps
Answer:
In: 33 Out: 29
In: 62 Out: 58
Step-by-step explanation:
Lets find the rate of change first;
\(\frac{y^{2}-y^{1} }{x^{2}-x^{1} }=\frac{15-5}{19-9}=\frac{10}{10}=1\)
for some particular value of , when is expanded and like terms are combined, the resulting expression contains exactly terms that include the four variables , , , and each to some positive power. what is ?
Answers
Using polynomial expansion, the resulting expression contains exactly 1001 terms that include all four variables a, b, c, and d, each to some positive power is 14.
According to the question,
For some particular value of N, when (a + b + c+ d+ 1)² is expanded and like terms are combined, the resulting expression contains exactly 1001 terms that include all four variables a, b, c, and d, each to some positive power.
Polynomial expansion :
(a + b)ⁿ = Cₙ⁰ aⁿ + Cₙⁿ⁻¹ aⁿ⁻¹ b + ....+ Cₙⁿbⁿ
\(x_{a} + x_{b} + x_{c} + x_{d} + x_{1}\) =N
\(x_{a} > 1 x_{b} > 1x_{c} > 1x_{d} > 1x_{1}\) >0
Positive integer solution:
\(x_{a} + x_{b} + x_{c} + x_{d} + x_{1}\) = N+1
Non - Negative integer solution:
\(x_{a} + x_{b} + x_{c} + x_{d} + x_{1}\) =N -4
C⁴ₙ = 1001
1001 = 7.11.13 after some trial and error we find that is N is equal to 14.
Hence, using polynomial expansion, the resulting expression contains exactly 1001 terms that include all four variables a, b, c, and d, each to some positive power is 14.
Learn more about Positive Power:
https://brainly.com/question/14786498
#SPJ4
I will mark you brainiest!!!
A passenger train left the station and traveled toward Las Vegas at an average speed of 55mph. A cattle train left at the same time and traveled in the opposite direction with an average speed of 65mph. Which equation best represents this situation when the trains are 960 mi apart?
A - 65x - 55(2) = 960
B - 65x - 55x = 960
C - 65x + 55(2) = 960
D - 65x + 55x = 960
E - 65(2) + 55x = 960
Answers
Answer:
The answer is b
Step-by-step explanation:
The distance traveled by the passenger train and the cattle train is equal to the total distance between them, which is 960 miles. Let x be the time (in hours) traveled by the passenger train and cattle train. Then, the equation that represents this situation is:
55x + 65x = 960
Simplifying the left-hand side of the equation, we get:
120x = 960
Dividing both sides by 120, we get:
x = 8
Therefore, the correct equation is:
B - 65x - 55x = 960
Jerome is making beef stew for his family. The recipe calls for 3.5 pounds (lbs.) of stew meat. He notices that he has 1.25 pounds (lbs.) in his refrigerator. How much stew meat should buy when he goes to the grocery in order to have enough? a) What operation (add, subtract, multiply or divide) would you use to solve this? b) How did you know?
Answers
EXPLANATION
Let's see the facts:
Call for---> 3.5 lbs of stew meat
Refrigerator -------> 1.25 lbs stew meat
He would buy:
Required - Available ----> 3.5 - 1.25 = 2.25 lbs of stew meat
The operation that we apply is subtraction because 3.5lbs (required) is greater than 1.25lbs (available).
how to change
a fraction into a percent
Answers
Answer:
[see below]
Step-by-step explanation:
If you are given a fraction, convert it into a decimal by diving the numerator by the denominator.
After converting it into a decimal, you multiply it by 100 to get the percent value. After that, you add the percent sign.
Example:
\(\text{Convert \frac{5}{10} into a percent.}\)\(\text{Convert } \frac{5}{10} \text{ into a percent.}\\\\\\\rightarrow \text{Step One: Convert into decimal.}\\\\\frac{5}{10}=0.5\\\\\rightarrow \text{Step Two: Multiply by 100 and then add percent sign.}\\\\0.5 * 100 = 50\\\\\)
50%
\(\frac{5}{10}=50\)%
Hope this helps.
Answer:
Divide the numerator into the denominator, then move the decimal 2 places to the right.
Step-by-step explanation:
Let's use 3/4 as an example.
Divide 3 into 4 and you get 0.75
Move the decimal 2 places to the right and you get 75
Then just add a percent sign (75%)
I hope this helps, and have a great day! :)
What would the green shapes be if the dimesions of the rectangular prism are 4 in by 4 in by 5 in? circle
Answers
The green shapes in the rectangular prism with dimensions 4 in by 4 in by 5 in would be circles.
In a rectangular prism, all faces are rectangles except for the two bases, which are squares when the prism is a right rectangular prism. Since the given dimensions of the rectangular prism are 4 in by 4 in by 5 in, the bases would be squares with sides measuring 4 in.
The question mentions green shapes, and based on the information provided, it can be inferred that the faces of the bases would be colored green. Since the bases are squares, the green shapes would be squares as well.
It's important to note that without further information or context, it is not possible to determine if any other faces or shapes within the rectangular prism are green. The given dimensions only indicate the shape of the bases, which are squares, and suggest that these squares could be colored green.
Learn more about rectangular prism visit:
brainly.com/question/21308574
#SPJ11
A. Use the AA Similarity Theorem in writing an if-then statement to describe the illustration
or in completing the figure based on the if-then statement.
R
Н.
If:
P
Then:
AHEY
Answers
The AA Similarity Theorem states that if two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. We can complete the figure by drawing a line segment of length 10.5 from point A to point H.
Using this theorem, we can write the following if-then statement to describe the given illustration:
If angle RH is congruent to angle A and angle NH is congruent to angle E, then triangle PHN is similar to triangle AHE.
This means that the corresponding sides of these triangles are proportional to each other. We can use this information to complete the figure by finding the length of side AH.
Since triangle PHN is similar to triangle AHE, we can set up the following proportion:
PH/AH = HN/HE
We know that PH = 6 and HN = 8, and we want to find AH. Let x represent the length of AH.
6/x = 8/14
Cross-multiplying gives us:
6 * 14 = 8 * x
Simplifying:
84 = 8x
Dividing both sides by 8:
x = 10.5
Therefore, we can complete the figure by drawing a line segment of length 10.5 from point A to point H.
To know more about Similarity Theorem, refer to the link below:
https://brainly.com/question/24167205#
#SPJ11
What is the volume of the figure?

Answers
volume= length x width x height
58:49 A pound of raisins costs $2.00, and a pound of almonds costs $5.00. Six pounds of a trail mix contains 2 more pounds of raisins than almonds. What is the cost of the 6 pounds of trail mix
Answers
Answer:
$18
Step-by-step explanation:
1 pound of raisins = $2
1 pound of almonds = $5
Let the number of raisins be represented by a
Let the number of almonds be represented by b
We are told in the question that:
Six pounds of a trail mix contains 2 more pounds of raisins than almonds.
a + b = 6 pounds
Hence, Almonds = 2 pounds
Raisins = 4 pounds
The cost of the 6 pounds of trail mix
= 4 × $2 + 2 × $5
=$8 + $10
= $18
Igor, whose eye height is 4. 5 ft. , wishes to find the height of an oak tree out in front of his castle. He places a mirror on the ground between himself and the tree. He is now 5. 5 feet away from the center of the mirror and the mirrors is 70 feet from the tree. What is the height of the oak tree in front of Igor´s castle?
Answers
The height of the oak tree in front of Igor's castle is approximately 57.27 ft. To find the height of the oak tree, we can use the principle of similar triangles.
The height of the tree can be determined by comparing the ratio of the height of Igor to the distance between Igor and the mirror with the ratio of the height of the tree to the distance between the mirror and the tree.
Let's represent the height of the oak tree as 'h'. According to the problem, Igor's eye height is 4.5 ft, and he is 5.5 ft away from the center of the mirror. The mirror is placed 70 ft from the tree.
Using the similar triangles concept, we can set up the following proportion:
(height of Igor) / (distance between Igor and mirror) = (height of tree) / (distance between mirror and tree)
Plugging in the given values, we have:
4.5 ft / 5.5 ft = h / 70 ft
Solving this proportion, we find:
(4.5 ft * 70 ft) / 5.5 ft = h.
For more such questions on Triangles:
https://brainly.com/question/2217700
#SPJ8
Answer the following questions below using the image

Answers
Answer:
A. 25:30
Sorry I'd help with the rest but my brain kinda died
A man traveled 1/3 of the distance between
two cities in 3/4 of an hour. At this rate, how
many hours will it take him to travel the
entire distance between the two cities?
Answers
Answer: 2 hours 15 minutes
Step-by-step explanation:
3/4 of an hour times 3 will be 9/4; each fourth is 15 minutes. 9 times 15 is 135 minutes, which is 2 hours and 15 minutes
Answer:
2.25 hours
Step-by-step explanation:
The man traveled 1/3 of the distance in 3/4 of an hour.
This means that he needs to travel for 3 times as long to travel the entire distance.
3 * 3/4 = 9/4 = 2.25
2.25 hours.
Or, 2 hours and 15 minutes (as 0.25 = 1/4).
The FDA regulates that fresh Albacore tuna fish contains at most 0.82 ppm of mercury. A scientist at the FDA believes the mean amount of mercury in tuna fish for a new company exceeds the ppm of mercury. The hypotheses are: H0:µ = 0.82 H1:µ > 0.82 What is a type II error in the context of this problem? A. The fish is accepted by the FDA when in fact it had more than 0.82 ppm of mercury. B. The fish is accepted by the FDA when in fact it had less than 0.82 ppm of mercury. C. The fish is rejected by the FDA when in fact it had less than 0.82 ppm of mercury. D. The fish is rejected by the FDA when in fact it had more than 0.82 ppm of mercury.
Answers
Answer:
Option A
Step-by-step explanation:
A type II error occurs when the researcher fails to reject the bull hypothesis when it is false.
In this study, the
null hypothesis is H0:µ = 0.82 while the alternative hypothesis is H1:µ > 0.82
Thus, the type II error will be that the fish is accepted by the FDA when in fact it had more than 0.82 ppm of mercury.
A smaller number is 3 less than half a larger number. The larger number is 10 times 1 less than the smaller number. Let x represent the smaller number, and let y represent the larger number. Which equations can be used to model the situation? Check all that apply. x = one-half y minus 3 2 x minus y = negative 6 2 x minus y = negative 3 x = one-half (y minus 3) y = 10 (x minus 1)
Answers
Answer:
Step-by-step explanation:
Represent the larger and the smaller numbers by y and x. Then:
y = 10(x - 1) and x = (y/2) - 3
Smaller number is 3 less than half a larger number is x=y/2-3 and larger number is 10 times 1 less than the smaller number is y=10(x-1)
What is Equation?Two or more expressions with an Equal sign is called as Equation.
Given that x represent the smaller number
Let y represent the larger number.
A smaller number is 3 less than half a larger number.
Half a larger number means 1/2 of y which is y/2.
3 less than half a larger number means y/2-3.
So smaller number is 3 less than half a larger number is x=y/2-3.
The larger number is 10 times 1 less than the smaller number.
The times in the sentence means product or multiplication.
So it can be represented by the equation as shown
y=10(x-1)
Hence, smaller number is 3 less than half a larger number is x=y/2-3 and larger number is 10 times 1 less than the smaller number is y=10(x-1).
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ5
Traingle A(1,8), M(6,8). P(2,3), is reflected over the x axis and then rotated 90degrees clockwise. What are the coordinates of its image A'M'P'?

Answers
Reflection over the x-axis transforms the point (x,y) into (x, -y), then
A(1,8) → A''(1, -8)
M(6,8) → M''(6, -8)
P(2,3) → P''(2, -3)
Rotation 90° clockwise transform the point (x, y) into (y, -x), then
A''(1, -8) → A'(-8, -1)
M''(6, -8) → M'(-8, -6)
P''(2, -3) → P'(-3, -2)
Assume that we have two events, A and B, that are mutually exclusive. Assume further that we know P(A) = 0.30 and P(B) =0.40. What is P(A | B)?
Answers
Answer:
0
Step-by-step explanation:
You want the probability P(A|B) when events A and B are mutually exclusive.
Conditional probabilityThe formula for conditional probability is ...
P(A|B) = P(A&B)/P(B)
When events are mutually exclusive, they occur together with probability 0 (never). Hence, ...
P(A|B) = 0/P(B)
P(A|B) = 0
determine the point estimate of the population proportion, the margin of error for each confidence interval, and the number of individuals in the sample with the specified characteristic, x, for the sample size provided. 11. Lower bound: 0.201, upper bound: 0.249, n = 1200 12. Lower bound: 0.051, upper bound: 0.074, n 1120
Answers
To determine the point estimate of the population proportion, we can take the midpoint of the confidence interval, which is (0.201 + 0.249) / 2 = 0.225.
To find the margin of error, we can use the formula:
margin of error = (upper bound - point estimate) / z*,
where z* is the z-score corresponding to the desired level of confidence. Let's assume a 95% confidence level, which corresponds to a z-score of 1.96.
margin of error = (0.249 - 0.225) / 1.96 = 0.0122
Therefore, the margin of error is approximately 0.0122.
Finally, we don't know the number of individuals in the sample with the specified characteristic, x, so we cannot determine this value.
Again, to determine the point estimate of the population proportion, we can take the midpoint of the confidence interval, which is (0.051 + 0.074) / 2 = 0.0625.
To find the margin of error, we can use the same formula as above:
margin of error = (upper bound - point estimate) / z*
Assuming a 95% confidence level:
margin of error = (0.074 - 0.0625) / 1.96 = 0.0059
Therefore, the margin of error is approximately 0.0059.
Finally, we don't know the number of individuals in the sample with the specified characteristic, x, so we cannot determine this value.
Visit here to learn more about population proportion brainly.com/question/15087042
#SPJ11