Answers
Answer:
\( log_{2}(9x) - log_{2}(3) = 3 \\ 3 = log_{2}(8) or log_{2}( {2}^{3} ) \\ log_{2}( \frac{9x}{3} ) = log_{2}(8) \\ \frac{9x}{3} = 8 \\ 9x = 8 \times 3 \\ 9x = 24 \\ x = \frac{24}{9} \\ x = \frac{8}{3} \\ x = 2 \times \frac{2}{3} \)
Answer:
\(\log _2\left(9x\right)-\log _2\left(3\right)=3 : x = \frac{8}{3}\)
Decimal:
\(x = 2.66666...\)
Step-by-step explanation:
\(\log _2\left(9x\right)-\log _2\left(3\right)=3\)
Add \(log _2\left(3)\) to both sides:
\(\log _2\left(9x\right)-\log _2\left(3\right)+\log _2\left(3\right)=3+\log _2\left(3\right)\)
Simplify:
\(\log _2\left(9x\right)=3+\log _2\left(3\right)\)
Use the logarithmic definition: If \(\log _a\left(b\right)=c\:\mathrm{then}\:b=a^c\)
\(\log _2\left(9x\right)=3+\log _2\left(3\right)\quad \Rightarrow \quad \:9x=2^{3+\log _2\left(3\right)}\)
\(9x=2^{3+\log _2\left(3\right)}\)
Expand \(2^{3+\log _2\left(3\right)} : 24\)
\(9x=24\)
Solve: \(9x=24 : x = \frac{8}{3}\)
\(x = \frac{8}{3}\)
Verify solutions: \(x = \frac{8}{3}\) : True
The solution is:
\(x=\frac{8}{3}\)
Hope I helped. If so, may I get brainliest and a thanks?
Thank you, have a good day! =)
Related Questions
please i need ASAPPPPP ILL GIVE BRAINLIEST!!!!
Hans baked 51 cookles. His family ate m of them. Using m, write an expression for the number of cookles that remained. + ローロ ロメロ
Answers
Answer:
\(51-m=n\)
Step-by-step explanation:
M - Number of cookies his family ate
N - The remaining number of cookies left
EASY POINTS!!
Find two numbers if....
Their sum is -7 and their difference is 14
Answers
Let
a------------> first number
b------------> second number
we know that
a+b=-7--------> a=-7-b----------> equation 1
a-b=14--------> equation 2
I substitute 1 in 2
(-7-b)-b=14-------------> -7-b-b=14----------> -7-2b=14-------> 2b=-7-14
2b=-21---------> b=-10.5
a=-7-b-------> a=-7-(-10.5)-----> a=-7+10.5------> a=3.5
the answer is
the two numbers are
a=3.5
and
b=-10.5
now gimme brainliest
Arrange the following fraction from least to greatest 2/3, 5/6, 3/5
What did you do to arrange the fraction from least to greatest?
Answers
Answer:
2/3 and 3/5 is same, then 5/6
Step-by-step explanation:
you can convert the fractions to decimals to find their value and then arrange them from least to the greatest.
Answer:
3/5, 2/3, 5/6 [From Least to Greatest]
Step-by-step explanation:
First you're going to want to know which one is "the bigger piece of pie".
I made a few drawing and look at the pictures (Just in case you have a different opinion from my answer)

Pls help asap
ivan made strawberry jam and raspberry jam. he made enough strawberry jam to fill 2/3 of a jar. if he made 4/5 as much raspberry jam as strawberry jam, how many jars will the raspberry jam fill?
write your answer as a fraction or as a whole or mixed number.
Answers
4/5 × 2/3
= (4×2)/(5×3)
=8/15
-6m+5p+7+8m-10
Help me
Answers
Answer:
add like terms the simplified answer is 2m+5p-3
Step-by-step explanation:
lmk if it is not supposed to be simplified
Julia surveyed twenty households on her street to determine the average number of children living in each household. the tables below represent the collected data and a randomly selected sample from the population. compare the mean of the population with the mean of the sample. population data 0 3 3 1 3 2 2 2 5 4 3 3 3 0 1 2 0 2 3 3 sample data 5 3 0 2 4 what is the difference between the mean of the sample and the mean of the population? 0.55 1.25 2.25 2.80
Answers
The difference between the mean of the sample and the mean of the population is A. 0.55
Calculations and Parameters:Given the population data is:
0 3 3 1 3 2 2 2 5 4 3 3 3 0 1 2 0 2 3 3
The sample data is:
5 3 0 2 4
The mean of the population data is:
45/20= 2.25
The mean of the sample data is:
14/5= 2.8
Therefore, the difference between the mean of the sample and the population is:
2.8-2.25= 0.55
Read more about mean here:
https://brainly.com/question/20118982
#SPJ4
30 POINTS BRAINLIEST HELPWhich number is rational? A-2.1010010001... b.-0.8974512... c.1.2547569... d. 5.3333333...
Answers
Answer:
Step-by-step explanation:
A rational number is a number that can be expressed as a ratio of two integers, or as a fraction. A rational number is any number that can be written in the form a/b, where a and b are integers and b is not equal to zero.
In this case, the correct answer is d. 5.3333333.... This number can be written as a fraction in the form 5 3/9, which is a ratio of two integers and thus a rational number.
The other three choices are not rational numbers because they are repeating decimals, or irrational numbers. An irrational number is a number that cannot be written as a ratio of two integers. Irrational numbers are numbers that are not rational.
For all numbers p and q, q = 5/3p + 46 . What is the value of pwhen the value of q is 21 ?
Answers
given that for all numbers of p and q,
q = 5/3p + 46
lets find p when q is 21
so lets substitute the value of q into the given equation
q = 5/3p + 46
21 = 5/3p + 46
lets collect like terms
21 - 46 = 5/3p
-25 = 5/3p
lets cross multiply
3 X -25 = 5p
-75 = 5p
5p = -75
divide both sides by 5
5p/5 = -75/5
p = -15
therefore for all values of p and q, q = 5/3p + 46,
the value of p is -15 when q is 21
If Michelle can ride her bike 5 miles in 20 minutes, how far can she ride her bike in 50 minutes?
Answers
Answer:
12.5 miles
Step-by-step explanation:
1 mile= 4 min.
x miles= 50 min.
1/4 = x/50
*cross multiply
4x= 50
divide by 4
x= 12.5 miles
Use the simplex algorithm to find the optimal solution to the following LP (solve manually): maxz= 36x1+30x2−3x3−4x4
s.t. x1+x2−x3≤5
6x1+5x2−x4≤10
∀xi≥0
Answers
The maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.
maximize: z = c1x1 + c2x2 + ... + cnxn
subject to
a11x1 + a12x2 + ... + a1nxn ≤ b1
a21x1 + a22x2 + ... + a2nxn ≤ b2
am1x1 + am2x2 + ... + amnxn ≤ bmxi ≥ 0 for all i
In our case,
the given LP is:maximize: z = 36x1 + 30x2 - 3x3 - 4x
subject to:
x1 + x2 - x3 ≤ 5
6x1 + 5x2 - x4 ≤ 10
xi ≥ 0 for all i
We can rewrite the constraints as follows:
x1 + x2 - x3 + x5 = 5 (adding slack variable x5)
6x1 + 5x2 - x4 + x6 = 10 (adding slack variable x6)
Now, we introduce the non-negative variables x7, x8, x9, and x10 for the four decision variables:
x1 = x7
x2 = x8
x3 = x9
x4 = x10
The objective function becomes:
z = 36x7 + 30x8 - 3x9 - 4x10
Now we have the problem in standard form as:
maximize: z = 36x7 + 30x8 - 3x9 - 4x10
subject to:
x7 + x8 - x9 + x5 = 5
6x7 + 5x8 - x10 + x6 = 10
xi ≥ 0 for all i
To apply the simplex algorithm, we initialize the simplex tableau as follows:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0 | 36 | 30 | -3 | -4 | 0 |
---------------------------------------------------------------------------
x5| 0 | 1 | 0 | 1 | 1 | -1 | 0 | 5 |
---------------------------------------------------------------------------
x6| 0 | 0 | 1 | 6 | 5 | 0 | -1 | 10 |
---------------------------------------------------------------------------
Now, we can proceed with the simplex algorithm to find the optimal solution. I'll perform the iterations step by step:
Iteration 1:
1. Choose the most negative coefficient in the 'z' row, which is -4.
2. Choose the pivot column as 'x10' (corresponding to the most negative coefficient).
3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.
Ratios: 5/0 = undefined, 10/(-4) = -2.5
4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.
5. Perform row operations to
make all other elements in the pivot column zero.
After performing these steps, we get the updated simplex tableau:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0.4 | 36 | 30 | -3 | 0 | 12 |
---------------------------------------------------------------------------
x5| 0 | 1 | -0.2 | 1 | 1 | -1 | 0 | 5 |
---------------------------------------------------------------------------
x10| 0 | 0 | 0.2 | 1.2 | 1 | 0 | 1 | 2.5 |
---------------------------------------------------------------------------
Iteration 2:
1. Choose the most negative coefficient in the 'z' row, which is -3.
2. Choose the pivot column as 'x9' (corresponding to the most negative coefficient).
3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.
Ratios: 12/(-3) = -4, 5/(-0.2) = -25, 2.5/0.2 = 12.5
4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.
5. Perform row operations to make all other elements in the pivot column zero.
After performing these steps, we get the updated simplex tableau:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0.8 | 34 | 30 | 0 | 4 | 0 |
---------------------------------------------------------------------------
x5| 0 | 1 | -0.4 | 0.6 | 1 | 5 | -2 | 10 |
---------------------------------------------------------------------------
x9| 0 | 0 | 1 | 6 | 5 | 0 | -5 | 12.5 |
---------------------------------------------------------------------------
Iteration 3:
No negative coefficients in the 'z' row, so the optimal solution has been reached.The optimal solution is:
z = 0
x1 = x7 = 0
x2 = x8 = 10
x3 = x9 = 0
x4 = x10 = 0
x5 = 10
x6 = 0
Therefore, the maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.
Learn more about Simplex Algorithm here:
https://brainly.in/question/46895640
#SPJ11
Can someone check this for me! I am not sure if I did this right


Answers
9514 1404 393
Answer:
8 seconds
Step-by-step explanation:
Your answer is the time interval at which the projectile is at or above ground level.
The way I read the question, it is asking for the value of t when the projectile hits the ground. It is 8 (seconds). My answer to this question would be 8, or 8 seconds.
__
Comment
We cannot tell whether the answer is intended to include units, or not. The usual clues are missing here.
In a contingency table, we describe the relationship between?
a. two variables measured at the ordinal or nominal level
b. two variables, one measured as an ordinal variable and the other as a ratio variable
c. two variables measured at the interval or ratio level
d. a variable measure on the interval or ratio level and time
Answers
In a contingency table, we describe the relationship between two variables measured at the ordinal or nominal level (option a).
A contingency table is a statistical table that displays the frequency distribution of two categorical variables and helps identify any associations or dependencies between them. The table organizes the data into rows and columns, with each cell representing the frequency count or proportion of observations falling into a particular combination of categories.
By examining the distribution of frequencies across the table, patterns and relationships between the variables can be discerned. This information can be useful in various fields, such as social sciences, market research, and epidemiology, for analyzing survey responses, understanding consumer preferences, or investigating the relationship between risk factors and diseases, among other applications.
To know more about contingency table, refer here:
https://brainly.com/question/30920745#
#SPJ11
refer to exhibit 9-6. at a .05 level of significance, it can be concluded that the proportion of the population in favor of candidate a is . a. not significantly greater than 80% b. significantly greater than 80% c. not significantly greater than 75% d. significantly greater than 75%
Answers
Based on this exhibit, a high school student is required to determine whether the proportion of the population in favor of candidate A is significantly option (b) or (c) greater than 80% or 75% at a 0.05 level of significance.
In statistical analysis, determining the proportion of a population in favor of a candidate or an idea is crucial in predicting election outcomes or measuring public opinion. Exhibit 9-6 presents statistical data on the proportion of the population in favor of candidate A
To answer this question, we need to conduct a hypothesis test and calculate the p-value. The null hypothesis (H0) states that the proportion of the population in favor of candidate A is equal to or less than the given proportion, while the alternative hypothesis (Ha) states that the proportion is greater than the given proportion. Therefore, the hypotheses can be stated as follows:
H0 => p ≤ 0.80 or p ≤ 0.75
H1 => p > 0.80 or p > 0.75
We then calculate the test statistic, which is the z-score. This can be done using the formula:
z = (p - p₀) / √(p₀(1-p₀)/n)
where p is the sample proportion, p₀ is the given proportion, and n is the sample size.
Next, we calculate the p-value, which is the probability of obtaining a test statistic as extreme as the observed one, assuming the null hypothesis is true. Since this is a one-tailed test, we use the standard normal distribution table and look up the area to the right of the calculated z-score. The p-value is the probability of getting a z-score as extreme or more extreme than the calculated one. If the p-value is less than the level of significance, we reject the null hypothesis and conclude that the alternative hypothesis is true.
To know more about proportion here.
https://brainly.com/question/30657439
#SPJ4
Suppose we had the following summary statistics from two different, independent populations, both with variances equal to σ.Population 1: ¯x1= 126, s1= 8.062, n1= 5Population 2: ¯x2= 162.75, s2 = 3.5, n2 = 4We want to find a 99% confidence interval for μ2−μ1. To do this, answer the below questions.
Answers
The confidence interval of 99% for μ₂ - μ₁ for the given mean and standard deviation is equal to (23.7377, 49.7713).
Confidence interval = 99%
Confidence interval for μ₂ - μ₁, we need to follow these steps,
Calculate the sample mean difference and the standard error of the mean difference.
Sample mean difference
= ¯x₂ - ¯x₁
= 162.75 - 126
= 36.75
Standard error of the mean difference
= √[(s₁^2/n₁) + (s₂^2/n₂)]
= √[(8.062^2/5) + (3.5^2/4)]
= 4.0065 (rounded to four decimal places)
The t-value for a 99% confidence level with degrees of freedom
= n₁ + n₂ - 2
= 5 + 4 - 2
= 7.
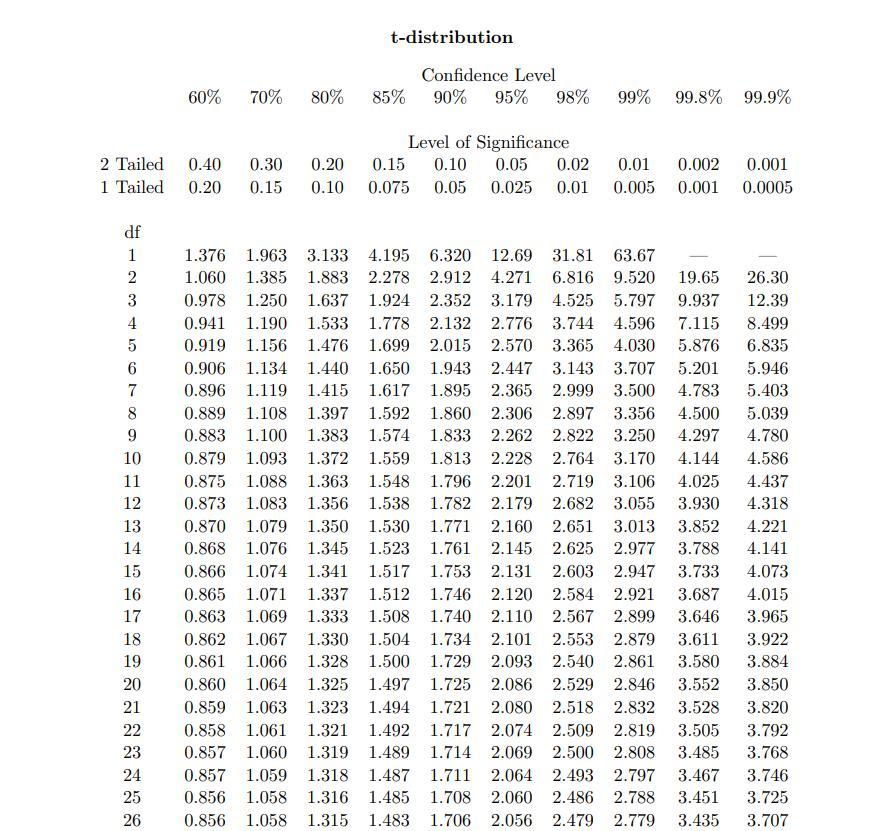
Using a t-distribution table attached ,
The t-value for a 99% confidence level with 7 degrees of freedom is 3.250.
Margin of error
= t-value x standard error of the mean difference
= 3.250 x 4.0065
= 13.0213 (rounded to four decimal places)
Confidence interval
= Sample mean difference ± Margin of error
= 36.75 ± 13.0213
= (23.7377, 49.7713)
Therefore, the 99% confidence interval for μ₂ - μ₁ is (23.7377, 49.7713).
learn more about confidence interval here
brainly.com/question/12977720
#SPJ4
The triangle circumscribes the circle. What is the perimeter of the triangle?

Answers
Answer:
P = 72 ft
Step-by-step explanation:
the perimeter P is the sum of the 3 sides.
Tangents to a circle from an external point are congruent , then
side 24 = 15 + 9
side 21 = 9 + 12
Third side = 12 + 15 = 27 ft
P = 24 + 21 + 27 = 72 ft
Help Me write the inequality that represents the number line! Sorry the picture is bad quality!

Answers
Answer:
x ≤ -6
Step-by-step explanation:
The line is moving towards the left, which means that the numbers are getting smaller. X is going to be less than something.
The dot on -6 is colored in. This means that -6 is included in our inequality. [X could equal -6]
So, we could write the equation x ≤ -6
Write the linear equation that gives the rule for this table.
x y
1 10
2 5
3 0
4 –5
Write your answer as an equation with y first, followed by an equal's sign.
Answers
The linear equation that gives the rule for this table is y = -5x + 15
How to determine the linear equation?The table of values is given as:
x y
1 10
2 5
3 0
4 –5
On the above table, we can see that:
As x increases by 1, the value of y decreases by 5
This means that the slope is
Slope = -5
Also, the above table can be modified as follows (using the slope of -5)
x y
0 15
1 10
2 5
3 0
4 –5
This means that the y-intercept is
y-intercept = 15
A linear equation is represented as
y = slope * x + y-intercept
So, we have
y = -5x + 15
So, the equarion is y = -5x + 15
Read more about linear equation at
https://brainly.com/question/13738662
#SPJ1
To save money at tennis pro company has manufactured a cylindrical tube that exactly fits three tennis balls if the diameter of the tube is 6.5 cm what is the volume of the air in the tube 
Answers
As the balls fit exactly into the tube we have:
Diameter of the tube = 6.5 cm so the radius = 3.25 cm. This is also the radius of the balls.
The height of the cylinder 3*6.5 = 19.5 cm.
So, volume of air
= pi*3.25^2*19.5 - 3*pi*3.25^2
= 99.55 cm^2 to nearest hundredth.
Find all solutions of the equation in the interval [0, 2π).
sinx = √1 - cosx
Write your answer(s) in radians in terms of π.
If there is more than one solution, separate them with commas.
Answers
The solutions for the equation sinx = √1 - cosx in the interval [0, 2π) are x = 0, π/2, and 3π/2.
To solve this equation, we first need to square both sides:
sin^2x = 1 - cosx
Next, we can use the identity sin^2x + cos^2x = 1 to substitute sin^2x with 1 - cos^2x:
1 - cos^2x = 1 - cosx
Now we can simplify by moving all the terms to one side:
cos^2x - cosx = 0
Factorizing, we get:
cosx(cosx - 1) = 0
So the solutions are when cosx = 0 or cosx = 1. In the interval [0, 2π), the solutions for cosx = 0 are x = π/2 and 3π/2. The solution for cosx = 1 is x = 0. Therefore, the solutions for the equation sinx = √1 - cosx in the interval [0, 2π) are x = 0, π/2, and 3π/2. We express these solutions in radians in terms of π.
To know more about equation visit:
https://brainly.com/question/29657983
#SPJ11
In the circle below, if < B = 46°, what is the measure of arc AB?
Select one:
a. 23°
b. 46°
c. 92°
d. 112

Answers
angle B = ( arc ADB ) ÷ 2
46 = ( arc ADB ) / 2
Multiply both sides by 2
46 × 2 = 2 × ( arc ADB ) / 2
92 = arc ADB
arc AB = arc ADB
arc AB = 92
The measure of arc AB is 92°. Therefore, option B is the correct answer.
Given that, ∠B = 46°.
We need to find the measure of arc AB.
What is an arc of a circle?The arc of a circle is defined as the part or segment of the circumference of a circle. A straight line that could be drawn by connecting the two ends of the arc is known as a chord of a circle. If the length of an arc is exactly half of the circle, it is known as a semicircular arc.
Now, ∠B = ( arc ADB ) ÷ 2
46° = ( arc ADB ) / 2
Multiply both sides by 2
46° × 2 = 2 × ( arc ADB ) / 2
92° = arc ADB
arc AB = arc ADB
arc AB = 92°
The measure of arc AB is 92°. Therefore, option B is the correct answer.
To learn more about the arc visit:
https://brainly.com/question/23117081.
#SPJ5
A store is offering a 20% discount on all items. Write an equation for the relationship between the discount price of an item, d , and it's original price, p.
Answers
Answer:
80%p=d
Step-by-step explanation:
20% discount is 80% of original.
An equation for the relationship between the discount price of an item, d, and it's original price, p is p = 0.8d.
What is a percentage?A ratio or value that may be stated as a fraction of 100 is called a percentage. And it is represented by the symbol '%'.
Given:
A store is offering a 20% discount on all items.
Let the discount price of an item, d, and it's original price, p.
The original price = (100 - 20%)discount price
p = 80%d
p = 0.8d
Therefore, p = 0.8d is the required equation.
To learn more about the percentage;
brainly.com/question/24159063
#SPJ5
Can someone please help me find the length and width please? 10 POINTS

Answers
Answer:
4.4 m
Step-by-step explanation:
The scale shows you the width of the bedroom is ...
1.2 + 2.1 + 1.1 = 4.4 . . . meters
helppp please this is homework you will be marked as brainlest

Answers
Answer:
Step-by-step explanation:

PLSSS HELP MEE
Equation: c² = n²
1. Take the square root of both sides of the equation and write the resulting equation.
2. Is there any way for this equation to be true? How?
Answers
1.
c² = n²
√c² = √n²
c = n
2.
if
c = 3 + 6 = 9
and
n = 5 + 4 = 9
Answer:
c = ±n
Step-by-step explanation:
Taking the square root of both sides yields
√c² = √n² or c = ±n
c² = n² is a quadratic equation, so we expect that there will be two roots: one positive and one negative.
Which of the following is equivalent to the expression? 22 - 2x - 3 Select one: 1) (x - 1)(x + 3) 2) (x - 2)(x - 1)3) (x + 1)(x - 3) 4) (2-2)(x + 1)

Answers
Explanation
\(x^2-2x-3\)Step 1
we have a expression in the form.
\(x^2-2x-3\Rightarrow wx^2+yx+z\)we need two a and b numbers such as
\(\begin{gathered} a+b=-2 \\ a\cdot b=-3 \\ \text{then a}\Rightarrow1,\text{ b}\Rightarrow-3 \\ 1-3=-2 \\ 1\cdot-3=-3 \end{gathered}\)now, we can factorize
\(\begin{gathered} x^2-2x-3=\mleft(x+a\mright)\mleft(x+b\mright) \\ x^2-2x-3=\mleft(x+1\mright)\mleft(x-3\mright) \end{gathered}\)I hope this helps you
At what annual interest rate, compounded annually, would $500
have to be invested for it to grow to $1,934.77 in 15 years?
Answers
The annual interest rate that $500 would have to be invested at to grow to $1,934.77 in 15 years is 6.6%.
The formula for compound interest is:
\(\begin{equation}A = P(1 + r)^t\end{equation}\)
Where:
A is the future value
P is the present value
r is the interest rate
t is the number of years
In this case, the future value is $1,934.77, the present value is $500, and the number of years is 15. Plugging these values into the formula, we get:
1934.77 = 500(1 + r)¹⁵
(1 + r)¹⁵ = 3.86954
1 + r = 1.066
r = 0.066
Therefore, the annual interest rate is 6.6%.
It is important to note that this is just an estimate. The actual interest rate that $500 would earn would depend on a number of factors, including the type of investment and the market conditions.
To know more about the annual interest rate refer here :
https://brainly.com/question/17403689#
#SPJ11
question is attached

Answers
f ( x ) = x² + 144
=> x² + 144 = 0
=> ( x + 12 ) ( x - 12 ) = 0
=> x + 12 = 0 and x - 12 = 0
=> x = -12 and x = 12
So,the zeroes of f are -12 and 12 .
It's vacation time. You drive 90 miles along a scenic highway and then take a 5-mile run along a hiking trail. Your driving rate is nine times that of your running rate. The graph shows the total time you spend driving and running, f(x), as a function of your running rate, x.
If the total time for driving and running is 3 hours, what is your running rate?
Answers
The running rate is 5 miles per hour.Let's denote the running rate as "r" and the driving rate as "9r" (since the driving rate is nine times the running rate).
To find the running rate, we need to determine the time spent driving and running separately and then add them together to equal 3 hours.
The time spent running can be calculated as the distance divided by the running rate:
Time running = Distance / Running rate = 5 / r
The time spent driving can be calculated similarly:
Time driving = Distance / Driving rate = 90 / (9r) = 10 / r
The total time spent driving and running is given as 3 hours:
Time running + Time driving = 3
5 / r + 10 / r = 3
To solve this equation, we can combine the fractions on the left side:
(5 + 10) / r = 3
15 / r = 3
Next, we can cross-multiply to isolate the variable:
15 = 3r
Dividing both sides by 3, we find:
r = 5
Therefore, the running rate is 5 miles per hour.
learn more about fractions here: brainly.com/question/10354322
#SPJ11
(a) Consider three sequences (an), (bn) and (sn) such that an ≤ sn ≤ bn for all n and lim an = lim b = s.Prove lim sn = s. This is called the "squeeze lemma." (b) Suppose (sn) and (tn) are sequences such that |sn| ≤ tn for all n and lim tn = 0. Prove lim sn = 0.
Answers
a. We have shown that lim sn = s when an ≤ sn ≤ bn for all n and lim an = lim bn = s, using the squeeze lemma.
b. We have shown that lim sn = 0 when sn ≤ tn for all n and lim tn = 0, using the squeeze lemma.
What is squeeze lemma?In mathematical analysis, the squeeze theorem—also referred to as the sandwich theorem, sandwich rule, police theorem, pinching theorem, and occasionally the squeeze lemma—is used to determine a function's limit when two other functions with known limits are also present.
(a) To prove that lim sn = s when an ≤ sn ≤ bn for all n and lim an = lim bn = s, we can use the squeeze lemma.
Since an ≤ sn ≤ bn for all n, we have 0 ≤ |sn - s| ≤ max{|an - s|, |bn - s|} for all n. Then, for any ε > 0, we can choose N such that |an - s| < ε and |bn - s| < ε for all n ≥ N. This implies that |sn - s| < ε for all n ≥ N, since |sn - s| ≤ max{|an - s|, |bn - s|} < ε. Therefore, by the definition of the limit, we have lim sn = s.
Thus, we have shown that lim sn = s when an ≤ sn ≤ bn for all n and lim an = lim bn = s, using the squeeze lemma.
(b) We have already proved in part (a) that lim sn = 0 when |sn| ≤ tn for all n and lim tn = 0, using the squeeze lemma. Therefore, to prove that lim sn = 0 when sn ≤ tn for all n and lim tn = 0, we can use the same argument.
Since sn ≤ tn for all n, we have -tn ≤ sn ≤ tn for all n. Then, taking the limit as n approaches infinity, we have:
lim (-tn) ≤ lim sn ≤ lim tn
Since lim tn = 0, we have lim (-tn) = -lim tn = 0. Therefore:
0 ≤ lim sn ≤ 0
By the squeeze lemma, we conclude that lim sn = 0.
Thus, we have shown that lim sn = 0 when sn ≤ tn for all n and lim tn = 0, using the squeeze lemma.
Learn more about squeeze lemma on:
https://brainly.com/question/18446513
#SPJ4
Triangle BCD, with vertices B(4,-7), C(6,-8), and D(7,-2), is drawn on the coordinate
grid below.
S
Answer: A =
6
7
D
9
What is the area, in square units, of triangle BCD?
units
Submit Answer
K

Answers
Answer: The area is 6.5
