Answers
The results for the variable t in each linear equation are listed below:
t = - 1t = - 24t = - 3t = - 2t = - 10How to solve linear equations by algebra properties
In this question we have linear equations with a single variable that must be cleared by using algebra properties. Now we proceed to solve each equation for the variable t:
Equation 1
16 · t + 4 · (5 - t) = 8
16 · t + 20 - 4 · t = 8
12 · t = - 12
t = - 1
Equation 2
18 = 2 · t - 3 · (t + 2)
18 = 2 · t - 3 · t - 6
24 = - t
t = - 24
Equation 3
- 10 · t - (t + 5) = 28
- 10 · t - t - 5 = 28
- 11 · t = 33
t = - 3
Equation 4
- 6 · (3 · t + 5) = 6
- 18 · t - 30 = 6
- 18 · t = 36
t = - 2
Equation 5
12 = 3 · (t + 14)
12 = 3 · t + 42
3 · t = - 30
t = - 10
To learn more on linear equations: https://brainly.com/question/13738061
#SPJ1
Related Questions
Expand and simplify 2(x+3y)+5(2x+y)
Answers
Answer:
Step-by-step explanation:
2(x+3y)+5(2x+y)
2x + 6y + 10x + 5y
Solving like terms
12x + 11y
array indices must be positive integers or logical values matlabtruefalse
Answers
True; In MATLAB, array indices must be positive integers or logical values.
In MATLAB, array indices must indeed be positive integers or logical values. This means that when accessing elements within an array, the index values should be integers greater than zero or logical values (true or false). It is not permissible to use negative integers or non-integer values as array indices in MATLAB.
For example, consider an array called "myArray" with five elements. To access the first element of the array, you would use the index 1. Similarly, to access the fifth element, you would use the index 5. Attempting to use a negative index or a non-integer index will result in an error.
Using valid indices is crucial for proper array manipulation and accessing the correct elements. MATLAB arrays are 1-based, meaning the index counting starts from 1, unlike some programming languages that use 0-based indexing.
In MATLAB, array indices must be positive integers or logical values. This ensures proper referencing and manipulation of array elements. By adhering to this rule, you can effectively work with arrays in MATLAB and avoid errors related to invalid indices.
To know more about
In MATLAB, array indices start from 1. They are used to access specific elements within an array.
In MATLAB, array indices are used to access or refer to specific elements within an array. The index of an element represents its position within the array. It is important to note that array indices in MATLAB start from 1, unlike some other programming languages that start indexing from 0.
For example, consider an array A with 5 elements: A = [10, 20, 30, 40, 50]. To access the first element of the array, we use the index 1: A(1). This will return the value 10.
Similarly, to access the third element of the array, we use the index 3: A(3). This will return the value 30.
Array indices can also be logical values, which are either true or false. Logical indices are used to select specific elements from an array based on certain conditions. For example, if we have an array B = [1, 2, 3, 4, 5], we can use logical indexing to select all the elements greater than 3: B(B > 3). This will return the values 4 and 5.
Learn more:About MATLAB here:
https://brainly.com/question/30763780
#SPJ11
What is the distance between points A and B?
A. -6 units
B. -1 units
C. 5 units
D 6 units

Answers
Answer:
6 units bro
Step-by-step explanation:
hoped this helped have a good day bay
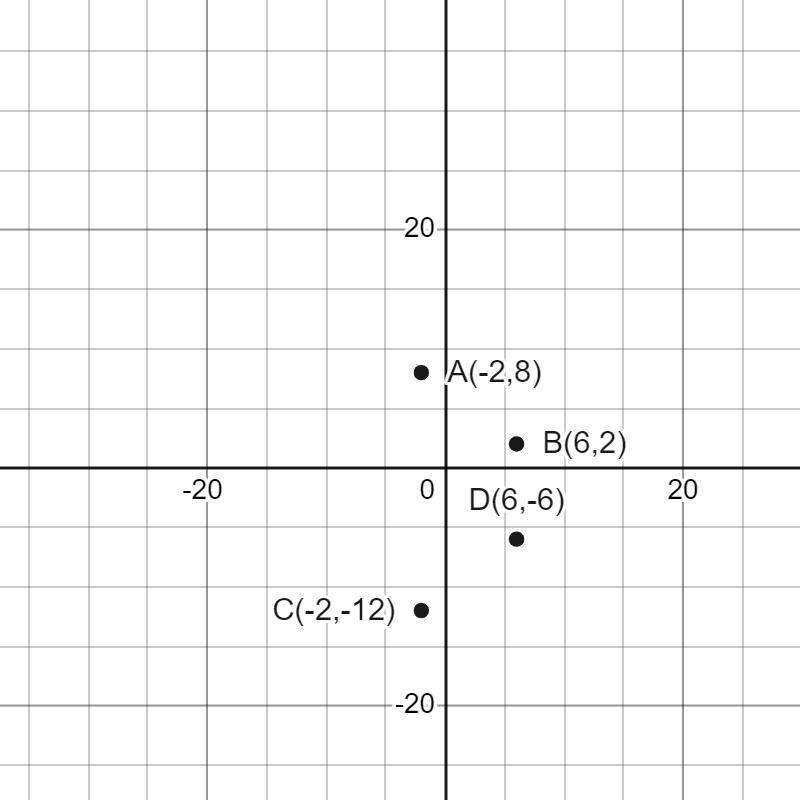
After a composition of transformations, the line segment from A(-2, 8) to B(6, 2) maps to the line segment C( -2, -12) to D(6, -6). Which of the following describes the composition that is applied to ⎯⎯⎯⎯⎯⎯⎯⎯AB¯ to obtain ⎯⎯⎯⎯⎯⎯⎯⎯⎯CD¯?

Answers
Given,
The coordinates of the point (-2, 8), (6,2), (-2, -12) and (6, -6).
Required
The composition required that is applied to to obtain .
The graph of the points are,
From the graph it is clear seen that
Reflect across the x axis and translate 4 units down.
Hence, Reflect across the x axis and translate 4 units down.
4. Brian is buying some tickets for his family
to go to a concert. The normal ticket
price for one person is £120. There are
discounts for booking early.
Adult tickets have 30% off the normal
price.
A child's ticket has 60% off the normal
price.
Brian buys two adult tickets
and three child's tickets with
the discount.
Work out how much he pays.
Answers
Answer:
312
Step-by-step explanation:
120x0.4=48
48x3=144
120x0.7=84
84x2=168
168+144=312
Spread of the student performance on assignment1 is higher for class A than class B. If we choose a student randomly from each class, then which student has a higher probability of taking values that are far away from the mean or expected value?
I have trouble understanding this question. What the correct answer is class A or class B?
Answers
Based on the given information that the spread of student performance on assignment1 is higher for class A than class B, the student from class A has a higher probability of taking values that are far away from the mean or expected value.
The spread of data refers to how much the individual values deviate from the mean or expected value. When the spread is higher, it means that the data points are more widely dispersed or varied. Therefore, in the context of student performance on assignment1, if the spread is higher in class A compared to class B, it implies that the individual student scores in class A are more likely to be farther away from the mean or expected value compared to class B.
In other words, class A may have a wider range of performance levels, including both higher and lower scores, compared to class B. This suggests that if a student is randomly chosen from each class, the student from class A is more likely to have a score that is far from the average or expected score of the class.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
On the previous screen, Irene matched these two cards.
What would you tell Irene to convince her that these cards don’t match?

Answers
The thing to tell Irene to convince her that these cards don’t match is that the addition of the variables will not give 4x + 2.
What is an expression?An expression can be used to illustrate the relationship between the variables that are given in the data.
The addition of the variables will be illustrated thus:
x + 2 + x + 2 + x + 2 + x + 2 = 28
4x + 8 = 28
In the question, it was written as 4x + 2 = 28. This shows that it won't match.
Learn more about expressions on:
brainly.com/question/723406
#SPJ1
Which system(s) of linear equations has (have) (2,−1) as its (their) unique solution? Select the THREE (3) systems that apply. Responses
Answers
The system of linear equations that has an unique solution has this feature:
Different slopes.
Then we must replace into the equations the variables x = 2 and y = -1, and verify if the equations are satisfied.
How to obtain the number of solutions of a system of equations?The slope-intercept definition of a linear function is given as follows:
y = mx + b.
In which:
The slope m represents the rate of change of the linear function.The intercept b represents the initial amount.The number of solutions for a system of two linear functions is defined as follows:
Zero solutions: same slope and different intercept.One solution: different slopes.Infinite solutions: same slope and same intercept.More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
a grocery store buys boxes of cereal for $ 2.00 each and sells them for 50% more. what does the grocery store charge its customers for each box of cereal?
Answers
Answer:
$3.00
Step-by-step explanation:
First find the markup
2.00 * 50%
2 * .5
1
Add this to the original price
2+1 =3
The store sells the cereal for $3.00
Answer:
$3
Step-by-step explanation:
The grocery store pays $2.00 for each box of cereal bought.
First, find 50% of the cost of each box:
2.00 x 0.50 = 1.00
Next, add the additional amount to the starting price:
2.00 + 1.00 = $3.00
$3.00 is your answer.
~
how do I find the inverse function of
Answers
To find the inverse function of F(x) = 2x - 3, we replace F(x) with y, swap the positions of x and y, and solve for y. The inverse function is f⁻¹(x) = (x+3)/2.
To find the inverse function of F(x) = 2x - 3, follow these steps
Replace F(x) with y. The equation now becomes y = 2x - 3.
Switch the positions of x and y, so the equation becomes x = 2y - 3.
Solve for y in terms of x. Add 3 to both sides: x + 3 = 2y.
Divide both sides by 2 (x + 3)/2 = y.
Replace y with the notation for the inverse function, f⁻¹(x): f⁻¹(x) = (x + 3)/2.
So, the inverse function of F(x) = 2x - 3 is f⁻¹(x) = (x + 3)/2.
To know more about inverse function:
https://brainly.com/question/17872426
#SPJ1
--The given question is incomplete, the complete question is given
" How do I find the inverse function of F(x) = 2x - 3"--
6sin^2 (x) + 6sin (x) + 1 = 0
solve and show steps for the graph ( i already have the graph )
Answers
To solve the equation \(6sin^2(x)\) + 6sin(x) + 1 = 0, we can use algebraic methods and the unit circle to determine the values of x that satisfy the equation.
1. Start by rearranging the equation to a quadratic form: \(6sin^2(x)\) + 6sin(x) + 1 = 0.
2. Notice that the equation resembles a quadratic equation in terms of sin(x). Let's substitute sin(x) with a variable, such as u: \(6u^2\) + 6u + 1 = 0.
3. Solve this quadratic equation for u. You can use the quadratic formula or factorization methods to find the values of u. The solutions are u = (-3 ± √3) / 6.
4. Since sin(x) = u, substitute back the values of u into sin(x) to obtain the values for sin(x): sin(x) = (-3 ± √3) / 6.
5. To find the values of x, we can use the inverse sine function. Take the inverse sine of both sides: x = arcsin[(-3 ± √3) / 6].
6. The arcsin function has a range of [-π/2, π/2], so the values of x lie within that range. Use a calculator to find the approximate values of x based on the values obtained in step 5.
7. Plot the obtained x-values on the graph to show the solutions of the equation \(6sin^2(x)\) + 6sin(x) + 1 = 0. The graph will illustrate the points where the curve intersects the x-axis.
For more such questions on algebraic, click on:
https://brainly.com/question/4344214
#SPJ8
Use the definition of Taylor series to find the Taylor series (centered at c ) for the function. f(x)=e 4x
,c=0 f(x)=∑ n=0
[infinity]
Answers
The answer is , the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
The Taylor series expansion is a way to represent a function as an infinite sum of terms that depend on the function's derivatives.
The Taylor series of a function f(x) centered at c is given by the formula:
\(\large f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(c)}{n!}(x-c)^n\)
Using the definition of Taylor series to find the Taylor series (centered at c=0) for the function f(x) = e^(4x), we have:
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{e^{4(0)}}{n!}(x-0)^n\)
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n\)
Therefore, the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
To know more about Function visit:
https://brainly.in/question/222093
#SPJ11
The Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To find the Taylor series for the function f(x) = e^(4x) centered at c = 0, we can use the definition of the Taylor series. The general formula for the Taylor series expansion of a function f(x) centered at c is given by:
f(x) = f(c) + f'(c)(x - c) + f''(c)(x - c)^2/2! + f'''(c)(x - c)^3/3! + ...
First, let's find the derivatives of f(x) = e^(4x):
f'(x) = d/dx(e^(4x)) = 4e^(4x)
f''(x) = d^2/dx^2(e^(4x)) = 16e^(4x)
f'''(x) = d^3/dx^3(e^(4x)) = 64e^(4x)
Now, let's evaluate these derivatives at x = c = 0:
f(0) = e^(4*0) = e^0 = 1
f'(0) = 4e^(4*0) = 4e^0 = 4
f''(0) = 16e^(4*0) = 16e^0 = 16
f'''(0) = 64e^(4*0) = 64e^0 = 64
Now we can write the Taylor series expansion:
f(x) = f(0) + f'(0)(x - 0) + f''(0)(x - 0)^2/2! + f'''(0)(x - 0)^3/3! + ...
Substituting the values we found:
f(x) = 1 + 4x + 16x^2/2! + 64x^3/3! + ...
Simplifying the terms:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
Therefore, the Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To know more about Taylor series, visit:
https://brainly.com/question/32235538
#SPJ11
the weights of oranges growing in an orchard are normally distributed with a mean weight of 8 oz. and a standard deviation of 2 oz. from a batch of 1400 oranges, how many would be expected to weigh more than 4 oz. to the nearest whole number? 1) 970 2) 32 3) 1368 4) 1295
Answers
The number of oranges that are expected to weigh more than 4 oz is:
1400 - (1400 × 0.0228)≈ 1368.
The mean weight of the oranges growing in an orchard is 8 oz and standard deviation is 2 oz, the distribution of the weight of oranges can be represented as normal distribution.
From the batch of 1400 oranges, the number of oranges is expected to weigh more than 4 oz can be found using the formula for the Z-score of a given data point.
\(z = (x - μ) / σ\)
Wherez is the Z-score of the given data point x is the data point
μ is the mean weight of the oranges
σ is the standard deviation
Now, let's plug in the given values.
\(z = (4 - 8) / 2= -2\)
The area under the standard normal distribution curve to the left of a Z-score of -2 can be found using the standard normal distribution table. It is 0.0228. This means that 0.0228 of the oranges in the batch are expected to weigh less than 4 oz.
To know more about normal distribution visit :
https://brainly.com/question/23418254
#SPJ11
Find the interquartile range of the following data set.
Number of Points Scored at Ten Basketball Games
48, 26, 31, 50, 38, 40, 42, 34, 44, 36
Im being timed
Answers
The Interquartile Range of the data set is 10
What is Interquartile Range?Interquartile Range is the difference in value between the upper quartile and lower quartile.
It is calculated using the formula: Interquartile Range = Q3 - Q1
How to determin the interquartile rangeFrom the question, we have:
48, 26, 31, 50, 38, 40, 42, 34, 44, 36
By arranging scores in ascending order, we get
26, 31, 34, 36, 38, 40, 42, 44, 48, 50
Q3 is the upper quartile i.e 75th percentile
75% of 10 = 7.5
This is approximately the 8th position i.e. Q3 = 44
Q1 is the lower quartile i.e 25th percentile
25% of 10 = 2.5
This is approximately the 3rd position i.e. Q1 = 34
Recall that
Interquartile Range = Q3 - Q1
So, we have
Interquartile range = 44 - 34
Evaluate
Interquartile range = 10
Hence, the value of the interquartile range is 10
Read more about quartiles at
https://brainly.com/question/30287732
#SPJ1
solve for x
explain how to do it pls

Answers
(15x+3)=108
x=7
if you plug 7 in for x
(15(7)+3) it equals 108
Brandon take a rectangular piece of fabric and make a diagonal cut from one corner to the oppoite corner. The cut he make i 13 inche long and the width of the fabric i 5 inche. What i the fabric' length?
Answers
The length of the fabric which Brandon formed a rectangle, is 11 inches.
To find the length of the fabric, we can use the Pythagorean theorem. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides.
In this case, the length of the fabric is one of the other two sides, and the diagonal cut is the hypotenuse. So, we can write the equation:
\(L^2 + 5^2 = 13^2\)
where L is the length of the fabric.
Solving for L, we get:
\(L^2 = 144 - 25 = 119, and L =\sqrt{119} = 11.\)
Learn more about the Pythagorean theorem here:
https://brainly.com/question/231802
#SPJ4
Question 2 For the following matrix Then [340]
A= [-127]
[-2-44]
(Please use a comma between two numbers.)
(a) The minors M13, M23, M33= 8,-4,10
(b)The cofactors C13, C23,C33= 8,4,10 (c) The determinant det(A) = 68
Answers
For the given matrix A, the minors M13, M23, M33 are 8, -4, and 10 respectively. The cofactors C13, C23, C33 are 8, 4, and 10 respectively. The determinant det(A) is 68.
To find the minors of a matrix, we need to find the determinants of the submatrices obtained by removing the row and column corresponding to the element of interest. In this case, the minors M13, M23, and M33 correspond to the determinants of the 2x2 submatrices obtained by removing the first row and the third column, second row and third column, and third row and third column, respectively.
To find the cofactors, we multiply each minor by a positive or negative sign based on its position in the matrix. The signs alternate starting with a positive sign for the top left element. In this case, the cofactors C13, C23, and C33 correspond to the minors M13, M23, and M33 respectively.
Finally, the determinant of a 3x3 matrix can be found by using the formula det(A) = a11C11 + a12C12 + a13C13, where a11, a12, and a13 are the elements of the first row of the matrix and C11, C12, and C13 are their corresponding cofactors. In this case, the determinant det(A) is 68.
Therefore, the minors M13, M23, M33 are 8, -4, and 10 respectively. The cofactors C13, C23, C33 are 8, 4, and 10 respectively. And the determinant det(A) is 68.
Learn more about submatrices here:
https://brainly.com/question/31669133
#SPJ11
Tele-Mart instituted a 5-for-1 split in April. After the split, Ashlee owned 1,860 shares. How many shares had she owned before the split?
Answers
Answer:
372 shares
Step-by-step explanation:
Let
x = shares owned before the split
Share after split : share before split = 5 : 1
Share after split : share before split = 1,860 : x
Equate both ratios
5 : 1 = 1,860 : x
5/1 = 1,860/x
Cross product
5 * x = 1 * 1,860
5x = 1,860
x = 1,860/5
x = 372
x = shares owned before the split = 372 shares
Complete the equation to make a true statement.
Enter your answer in the box.

Answers
Applying the power of power rule, the completed equation is given as follows:
\(x^{10} = (x^5)^2\)
How to use the power of power rule?The power of a power rule is used when a single base is elevated to multiple exponents, and states that simplified expression is obtained keeping the base, while the exponents are multiplied.
Hence the missing exponent for this problem is obtained as follows:
2x = 10
x = 10/2
x = 5.
More can be learned about the power of a power property at brainly.com/question/11975096
#SPJ1
-5 + 6 answer this question for 30 points
Answers
Answer:
-5/6 ___ -0.1
Step-by-step explanation:
Write an explicit formula for the sequence 1,4,7,10... Then find a14.
Answers
Answer:
The formula is \(a_n = 3n-2\)
The 14th term is 40, in other words, \(a_{14} = 40\)
========================================================
Explanation:
The given sequence is 1, 4, 7, 10, ...
Subtract each adjacent term:
4-1 = 37-4 = 310-7 = 3This shows that each term is increasing by 3. This is the common difference, so d = 3.
The first term is \(a_1 = 1\)
The nth term of the arithmetic sequence is...
\(a_n = a_1 + d(n-1)\\\\a_n = 1 + 3(n-1)\\\\a_n = 1 + 3n-3\\\\a_n = 3n-2\\\\\)
As a check, let's plug in say n = 3 to find that:
\(a_n = 3n-2\\\\a_3 = 3(3)-2\\\\a_3 = 9-2\\\\a_3 = 7\\\\\)
The third term is 7, which matches with the sequence given to us. I'll let you confirm the other values.
-----------
We'll repeat this idea but now for n = 14 to find the 14th term of the sequence.
\(a_n = 3n-2\\\\a_{14} = 3(14)-2\\\\a_{14} = 42-2\\\\a_{14} = 40\\\\\)
The 14th term is 40.
You can make a table of values to help confirm the answer. In the first column you'll have the values of n (1,2,3,...) all the way up to 14. The second column will consist of the sequence 1, 4, 7, 10, ... each time going up by 3 until you reach the 14th term of 40.
when preparing to go shopping after the christmas holidays, conley actively scans the ads in the local newspaper for coupons and contests. while in the store, conley also looks for free samples of new products and products she hasn't purchased previously. the coupons, contests, and free samples are all examples of
Answers
promotional strategies used by companies to draw clients and boost sales. For example, product promotions include free samples, whereas sales promotions include coupons and competitions.
Sales promotions are short-term incentives provided by businesses to entice clients to make a purchase or carry out a specific action, such redeeming a coupon or participating in a competition. On the other hand, product promotions use free samples to spread the word about and encourage people to try a new or existing product.
The coupons, contests, and free samples that Conley is looking for while preparing to go shopping after the Christmas holidays are all examples of promotional tools or marketing strategies used by companies to attract customers and boost sales. Samples are a particularly effective marketing tool as they allow customers to try products before purchasing them, increasing the likelihood of a sale. Conley's proactive approach to finding these promotional tools and taking advantage of them demonstrates her savvy consumer skills.
To know more about sales promotions Visit:
https://brainly.com/question/13975307
#SPJ11
what is the best big-o function for the worst case scenario analysis of a linar search of a list of size n (counting the number of comparisons)?
Answers
Big O notation focuses on the worst-case scenario analysis, which is 0(n) for a simple search. It’s a reassurance that a simple search will never be slower than O(n) time.
Imagine that you're a teacher with a student named Ram. You want to find his records, so you use a simple search algorithm to go through your school district's database.
You know that a simple search takes O(n) times to run. This means in the worst case, you'll have to search through every single record to find Ram
After a simple search, you find that Ram records are the very first entry in the database. You don't have to look at every entry.
Did this algorithm take O(n) time Or did it take O(1) time because you found Ram records on the first try?
In this case, 0(1) is the best-case scenario – you were lucky that Ram records were at the top. But Big O notation focuses on the worst-case scenario, which is 0(n) for a simple search. It’s a reassurance that a simple search will never be slower than O(n) time.
Learn more about Big-o from
https://brainly.com/question/13257594
#SPJ4
how to know if a function has a vertical asymptote
Answers
To determine if a function has a vertical asymptote, you need to consider its behavior as the input approaches certain values.
A vertical asymptote occurs when the function approaches positive or negative infinity as the input approaches a specific value. Here's how you can determine if a function has a vertical asymptote:
Check for restrictions in the domain: Look for values of the input variable where the function is undefined or has a division by zero. These can indicate potential vertical asymptotes.
Evaluate the limit as the input approaches the suspected values: Calculate the limit of the function as the input approaches the suspected values from both sides (approaching from the left and right). If the limit approaches positive or negative infinity, a vertical asymptote exists at that value.
For example, if a rational function has a denominator that becomes zero at a certain value, such as x = 2, evaluate the limits of the function as x approaches 2 from the left and right. If the limits are positive or negative infinity, then there is a vertical asymptote at x = 2.
In summary, to determine if a function has a vertical asymptote, check for restrictions in the domain and evaluate the limits as the input approaches suspected values. If the limits approach positive or negative infinity, there is a vertical asymptote at that value.
know more about vertical asymptote.
https://brainly.com/question/29260395
#SPJ11
Evaluate the line integral, where C is the given curve.
∫C xy dx +(x - y)dy
C consists of line segments from (0, 0) to (4, 0) and from (4, 0) to(5, 2).
I've looked at the example problem from the book but somehow Icannot get it using the numbers given. I think I may besetting it up incorrectly. Help is appreciated!
Answers
To evaluate the line integral, we need to parametrize the given curve C and then substitute the parametric equations into the integrand. We can parameterize C using two line segments as follows:
For the first line segment from (0, 0) to (4, 0), we can let x = t and y = 0, where 0 ≤ t ≤ 4.
For the second line segment from (4, 0) to (5, 2), we can let x = 4 + t/√5 and y = 2t/√5, where 0 ≤ t ≤ √5.
Then the line integral becomes:
∫C xy dx +(x - y)dy = ∫0^4 t(0) dt + ∫0^√5 [(4 + t/√5)(2t/√5) dt + (4 + t/√5 - 2t/√5)(2/√5) dt]
Simplifying the integrand, we get:
∫C xy dx +(x - y)dy = ∫0^4 0 dt + ∫0^√5 [(8/5)t^2/5 + (8/5)t - (2/5)t^2/5 + (8/5)] dt
Evaluating the definite integral, we get:
∫C xy dx +(x - y)dy = [(8/25)t^5/5 + (4/5)t^2/2 + (8/5)t]0^√5 + [(2/25)t^5/5 + (4/5)t^2/2 + (8/5)t]0^√5
Simplifying, we get:
∫C xy dx +(x - y)dy = (16/5)(√5 - 1)
Therefore, the value of the line integral is (16/5)(√5 - 1).
To know more about line integral , refer here :
https://brainly.com/question/30763905#
#SPJ11
I need to solve for h. V=1/3 s square h
Answers
Since the given equation is
\(V=\frac{1}{3}sh^2\)We need to solve for each, then
We have to isolate h on one side and the other terms on the other side
Then multiply both sides by 3
\(\begin{gathered} (3)\times V=\frac{1}{3}\times(3)sh^2 \\ 3V=sh^2 \end{gathered}\)Now, divide both sides by s
\(\begin{gathered} \frac{3V}{s}=\frac{sh^2}{s} \\ \frac{3V}{s}=h^2 \\ h^2=\frac{3V}{s} \end{gathered}\)Take a square root for both sides
\(\begin{gathered} \sqrt[]{h^2}=\pm\sqrt[]{\frac{3V}{s}} \\ h=\pm\sqrt[]{\frac{3V}{s}} \end{gathered}\)(I'll give brainliest!!) Which equation applies the associative property of multiplication?

Answers
The equation that applies the associative property of multiplication is given as follows:
(-9/4 x 3/2) x (6/3 x 5/7) = -9/4 x (3/2 x 6/3) x 5/7.
Associative property of multiplicationThe associative property of multiplication expresses that if three numbers are multiplied, the order of the parenthesis is not relevant to the product, that is, it does not change the result of the multiplication.
The associative property of multiplication can be symbolized as follows:
(a x b) x c = a x (b x c)
With three terms.
In this problem, the associative property of multiplication is represented with four terms in the second expression, as follows:
(-9/4 x 3/2) x (6/3 x 5/7) = -9/4 x (3/2 x 6/3) x 5/7.
More can be learned about the associative property of multiplication at https://brainly.com/question/17176614
#SPJ1
Write each polynomial in standard form. Then classify it by degree and by number of terms. x² - x⁴+2x² .
Answers
The polynomial x² - x⁴ + 2x² in standard form is x⁴ + 3x² and it is a fourth-degree polynomial and it consists of two terms.
To write the polynomial x² - x⁴ + 2x² in standard form, we arrange the terms in descending order of degree:
x⁴ + 2x² + x²
Simplifying the terms:
x⁴ + 3x²
Now, let's classify the polynomial by degree and number of terms:
The highest power of x in the polynomial is x⁴, so the degree of the polynomial is 4.
The polynomial has two terms, namely -x⁴ and 3x².
Therefore, we can classify the polynomial x² - x⁴ + 2x² as a fourth-degree polynomial and it consists of two terms.
To learn more on Polynomials click:
https://brainly.com/question/11536910
#SPJ4
A manufacturing company buys a new stamping machine for $28,000. The maker of the machine informs the company’s CEO that on average, it depreciates in value according to the schedule shown in the table. Answer the questions that follow.
Months
Value
0
$28,000
6
$24,500
12
$21,000
18
$17,500
24
$14,000
Answer the following questions
1) If the depreciation continues at the same rate, how long will it take until the machine has no value?
2) Based on the pattern you see in the table, how do you know that the graph will be a straight line?
3) Enter the values in the table above in an Excel spreadsheet and use Excel to create a line graph. Label the axes and title the graph. Then copy the graph from your Excel spreadsheet and paste it below.
4) Find the slope of the graph and explain what it means.
5) Find the intercepts of the graph, and describe what each intercept means.
6) If we use the letter x to represent the variable number of months, write an expression that represents the value of the machine.
7) Use your expression from Question 6 to find when the machine has no value, and compare it to the answer you have in Question 1. Do you get the same/different answers? Explain.
Answers
1.The machine will have no value after 48 months. 2.The graph of the machine's value over time will be a straight line. 3.The slope of the graph represents the rate of depreciation per month. 4.The intercepts of the graph indicate the initial value and zero value. 5.The expression V = -750x + 28,000 represents the value of the machine. 6.The machine has no value when x = 37 according to the expression. 7.The answer obtained using the expression differs from the answer in 8.question 1 due to possible rounding errors or calculation variations.
To determine when the machine has no value, we observe the pattern of depreciation. Based on the given data, the machine depreciates by $3,500 every 6 months. Therefore, it will take 48 months (8 cycles of 6 months) for the machine to have no value.
The table shows a consistent decrease in value over time with equal intervals of 6 months. This indicates a linear relationship between the number of months and the value. A linear relationship is represented by a straight line on a graph.
The slope of the graph can be determined by calculating the change in value divided by the change in time. In this case, the slope is (-750), meaning the value decreases by $750 per month. It represents the rate of depreciation per month.
The intercepts of the graph are obtained by determining the value of the machine at the start (initial value intercept) and when it reaches zero (zero value intercept). The initial value intercept is $28,000, which represents the starting value of the machine. The zero value intercept occurs when the machine has no value.
The expression V = -750x + 28,000 represents the value of the machine. The coefficient of x (-750) represents the rate of depreciation per month, while the constant term (28,000) represents the initial value.
Using the expression, when x = 37, the machine has no value. This differs from the answer in question 1 (48 months). The discrepancy could be due to rounding errors or variations in the method used to calculate the exact point at which the value reaches zero.
learn more about initial value intercept here:
https://brainly.com/question/20726576
#SPJ11
What is the product?
(5r − 4)(r2 − 6r + 4)
Answers
Answer:
1r
Step-by-step explanation:
(5r-4)(2r-6r+4)
1(5r-4)+1(2r-6r+4)
5r-4+2r-6r+4
5r+2r-6=1r
1r-4+4
-4+4=0
1r
