Answers
Answer:
A) Second step
would be the answer
Related Questions
haswell enterprises' bonds have a 10-year maturity, a 6.25% semiannual coupon, and a par value of $1,000. the going interest rade is 4.75%
Answers
The price of the Haswell Enterprises' bond is $1,124.61.
Step 1: To calculate the bond price we need to use the present value formula, which takes into account the future cash flows discounted by the market interest rate.
Step 2: First, we need to calculate the number of periods, since the bond pays a semiannual coupon and has a 10-year maturity. There are 20 semiannual periods (10 years \(\times\) 2 semiannual periods per year).
Step 3: Next, we need to calculate the semiannual coupon payment. The coupon rate is 6.25%, which means the bond pays a semiannual coupon of:
Coupon payment = Coupon rate \(\times\) Par value / 2
Coupon payment = 6.25% \(\times\)$1,000 / 2
Coupon payment = $31.25
Using the present value formula, the bond price can be calculated as:
Price of bond = (Coupon payment / (1 + Market interest rate/2\()^1\)) + (Coupon payment / (1 + Market interest rate/2\()^2\)) + ... + (Coupon payment + Par value / (1 + Market interest rate/2\()^{20}\))
where:
Market interest rate is 4.75% (semiannual)
Coupon payment is $31.25
Par value is $1,000
Plugging in the values, we get:
Bond price = ($31.25 / (1 + 4.75%/2\()^1\)) + ($31.25 / (1 + 4.75%/2\()^2\)) + ... + ($31.25 + $1,000 / (1 + 4.75%/2\()^{20}\))
Price of bond = $1,124.61
Therefore, the price of the Haswell Enterprises' bond is $1,124.61.
To know more about Bond price visit:
https://brainly.com/question/15518377
#SPJ11
If 4 g
of salt dissolved in 200 g of water, what would be the final mass of
this mixture?
A. 50 g
B. 196 g
C. 204 g
D. 800 g
Answers
Answer:
C
Step-by-step explanation:
200g + 4g = C. 204 g
Mass is the quantity of matter present in a substance. Density is the ratio of mass to volume. It is given by:
Density = mass/ volume
Given that a 4g salt is dissolved in 200 g of water. Hence:
Final mass of mixture = mass of salt + mass of water
Final mass of mixture = 4g + 200g = 204g
The final mass of this mixture is 204g
Find out more on mass at: https://brainly.com/question/15526412
A triangular prism. The triangular base has a base of 11 inches and height of 7 inches. The height is 9 inches. The formula for volume of a prism is V = Bh. The variable B stands for the . In this prism, B equals in.2. The variable h stands for . In this prism, h is in. The volume of the prism is in.3. This question is from e2020
Answers
Answer:
Variable B is the area of triangular base.
B = 38.5 \(in^{2}\).
Variable h is the height of pyramid.
In the given prism, h is 9 inches.
The volume of prism is 346.5 \(in^{3}\).
Step-by-step explanation:
Please refer to the attached image for the detailed labeling of all the sides.
\(\triangle ABC\) is the triangular base of the prism.
BC is the base of triangular base of the prism.
AP is the height of triangular base.
Area of triangular base is represented by B and is calculated by following formula of area of a triangle.
\(Area = \dfrac{1}{2} \times \text{Base}\times \text{Height}\)
\(\Rightarrow \dfrac{1}{2} \times 11 \times 7\\\Rightarrow 38.5\ in^{2}\)
Hence, B = 38.5 \(in^{2}\).
Height of prism, h = 9 in
h is represented as side BE in the attached image.
It is know that volume of prism is given as :
V = Bh
Putting values of B and h:
\(V = 38.5 \times 9\\\Rightarrow V = 346.5\ in^{3}\)

Answer:
The formula for volume of a prism is V = Bh.
The variable B stands for the ✔ area of the base.
In this prism, B equals ✔ 38.5 in.².
The variable h stands for ✔ height.
In this prism, h is ✔ 9 in.
The volume of the prism is ✔ 346.5 in.³.
Explanation:
The answer above mine is correct. I hope this helps!
Alice, Bob, Carol, and Dave are playing a game. Each player has the cards {1,2, ...,n} where n ≥ 4 in their hands. The players play cards in order of Alice, Bob, Carol, then Dave, such that each player must play a card that none of the others have played. For example, suppose they have cards {1, 2, ...,5}, and suppose Alice plays 2, then Bob can play 1, 3, 4, or 5. If Bob then plays 5, then Carol can play 1, 3,
or 4. If Carol then plays 4 then Dave can play 1 or 3.
(a) Draw the game tree for n = 4 cards. (b) Consider the complete bipartite graph K4n. Prove a bijection between the set of valid games for n
cards and a particular subset of subgraphs of K4.n.
Answers
(a) The game tree for n = 4 cards can be represented as follows:
markdown
Alice
/ | | \
1 3 4 5
/ | \
Bob | Dave
/ \ | / \
3 4 5 1 3
b here is a bijection between the set of valid games for n cards and a particular subset of subgraphs of K4.n.
In this game tree, each level represents a player's turn, starting with Alice at the top. The numbers on the edges represent the cards played by each player. At each level, the player has multiple choices depending on the available cards. The game tree branches out as each player makes their move, and the game continues until all cards have been played or no valid moves are left.
(b) To prove the bijection between the set of valid games for n cards and a subset of subgraphs of K4.n, we can associate each player's move in the game with an edge in the bipartite graph. Let's consider a specific example with n = 4.
In the game, each player chooses a card from their hand that hasn't been played before. We can represent this choice by connecting the corresponding vertices of the bipartite graph. For example, if Alice plays card 2, we draw an edge between the vertex representing Alice and the vertex representing card 2. Similarly, Bob's move connects his vertex to the chosen card, and so on.
By following this process for each player's move, we create a subgraph of K4.n that represents a valid game. The set of all possible valid games for n cards corresponds to a subset of subgraphs of K4.n.
Therefore, there is a bijection between the set of valid games for n cards and a particular subset of subgraphs of K4.n.
Learn more about subgraphs here:
brainly.com/question/32421913
#SPJ11
Help please giving out Brianlest thank you very much

Answers
Answer:
5/6
Step-by-step explanation:
See attached Venn diagram
Given they passed the test is 12
then 10 of these completed the assignment 10 /12 = 5/6

find this using the box method

Answers
Upper right -12
Lower left 2x^2
Bottom right 8x
Product 2x^2-3x+8x-12
Sum 2x^2+5x-12
Solve for x in the equation x2-10x+25= 35-
X=5+2√ √5
O x=5± √√35
x=10+2√√/5
x = 10+ √√√35
0 0 0 0
Answers
The solution of the quadratic equation is x=5±√35 .
A quadratic equation is given by the equation which can be written in the form ax²+bx +c.
There are two solution of x for a quadratic equation. the graph of a quadratic equation is in the shape of a parabola in the cartesian plane.To solve a quadratic equation various methods are used:Completing of squaresMiddle term factorizationusing the quadratic formulathe given quadratic equation is :
x²-10x+25=35
Simplifying the equation we get:
or, x²-10x+25-35=0
or, x²-10x-10=0
Now we will solve the equation by completion squares method:
x²-10x-10=0
or, x²-2×x×5+5²-5²-10=0
or, (x-5)²=35
or, x-5=±√35
or, x= 5±√35
Therefore the solution of the quadratic equation is 5+√35 and 5-√35 .
To learn more about quadratic equations visit:
https://brainly.com/question/17177510
#SPJ9
PLEASEEEEEE HELPPPPPPPP I’ll MAKE YOU BRAINLY
When viewed from the side, the frame of a ball-return net
angles with the ground.
forms a pair of supplementary
Find m/BCE and mZECD.

Answers
Answer:
BCE= 115 ECD=65
Step-by-step explanation:
(5x+10)+(3x+2)=180
8x+12=180
8x=168
x=21
5(21)+10=115
3(21)+2=65
Answer:
<BCE=115°
<ECD=65°
And their sum is 180°
Step-by-step explanation:
< BCE + <ECD =180° ( Being sum of supplementary angle which is formed in the given diagram is 180°)
(5x + 10)° + (3x + 2)°= 180°
5x + 10 + 3x + 2 = 180°
5x + 3x + 10 +2 = 180°
8x + 12= 180°
8x = 180°-12°
8x = 168
x= 168/8
x=21°
Now,
<BCE = 5x+10
= 5*21+10
=105+10
=115
<ECD
= 3x+2
= 3*21+2
=65
Find x:
M
Х
60° 60°
L
N
16

Answers
its 7.5 im pretty sure
Please Help! You Dont Have To do the Bottom Questions Just The Top!
Answers
a. 0.5 + 0.3 = 0.8
b. 2.7 + 28.8 = 30.9
c. 3.1 + 2.4 + 9.9 = 15.4
d. 15.2 + 1.4 + 0.8 = 17.8
e. 39.2 + 2.5 + 0.8 = 42.3
Step-by-step explanation:
a. 0.54 rounded to the nearest 10th will be 0.5 because 4 doesn't round up numbers. 0.278 rounded to the nearest tenth will be 0.3 because any number equal to or greater than 5 rounds up the number in front of itself. When you add 0.5 and 0.3, you get 0.7.
b. 2.65 rounded to the nearest 10th will be 2.7 because any number equal to or greater than 5 rounds up the number in front of itself. 28.17 rounded to the nearest 10th will be 28.2 because any number equal to or greater than 5 rounds up the number in front of itself. When you add 2.7 and 28.2 you get 30.9.
c. 3.09 rounded to the nearest 10th will be 3.1 because any number equal to or greater than 5 rounds up the number in front of itself. 2.41 rounded to the nearest 10th will be 2.4 because 4 doesn't round up the number. 9.86 rounded to the nearest 10th will be 9.9 because any number equal to or greater than 5 rounds up the number in front of itself. When you add 3.1 + 2.4 + 9.9, you get 15.4.
d. 15.234 rounded to the nearest 10th will be 15.2 because 3 doesn't round up the number. 1.37 rounded to the nearest 10th will be 1.4 because any number equal to or greater than 5 rounds up the number in front of itself.
0.76 rounded to the nearest 10th will be 0.8 because any number equal to or greater than 5 rounds up the number in front of itself. When you add 15.2 + 1.8 + 0.8, you get 17.8.
e. 39.18 rounded to the nearest 10th will be 39.2 because any number equal to or greater than 5 rounds up the number in front of itself. 2.48 rounded to the nearest 10th will be 2.5 because any number equal to or greater than 5 rounds up the number in front of itself. 0.84 rounded to the nearest 10th will be 0.8 because 4 doesn't round up the number. 39.2 + 2.3 + 0.8 = 42.3
Select the correct answer from each drop-down menu.The figure shown consists of a square pyramid on top of a square prism. The surface area of the figure is 432 cm? The height of the prism isthree times the height of the pyramid.3h8 cmFind the heights of the pyramid and the prism.The height of the pyramid is vcmThe height of the prism is V cm

Answers
Answer:
Explanation:
Given;
Surface area of the figure = 432 cm^2
Length of the square base(l) = 8cm
Height of the prism = 3 times height of the pyramid
We'll use the below formula for the surface area(SA) of the figure to determine the height of the pyramid;
\(undefined\)In the accompanying diagram, tangent PA and secant PBC are drawn to circle O from point P. If mAC=80 and mAB=60, what is the measure of

Answers
The measure of angle APB in the intersecting chords is 10⁰.
What is the measure of angle APB?
The measure of angle APB is calculated by applying intersecting chord theorem which that the angle at tangent is half of the arc angle of the two intersecting chords.
The value of m∠APB is calculated as follows;
m∠APB = ¹/₂ (arc AC - arc AB ) ( exterior intersecting secants)
The value of arc angle AC = 80⁰
The value of arc angle AB = 60⁰
Now substitute and solve for the value of angle APB as follows;
m∠APB = ¹/₂ (80 - 60 )
m∠APB = ¹/₂ ( 20 )
m∠APB = 10⁰
Learn more about chord angles here: brainly.com/question/23732231
#SPJ1
The complete question is below:
In the accompanying diagram, tangent PA and secant PBC are drawn to circle O from point P. If mAC=80 and mAB=60, what is the measure of angle APB.
Which equation can be used to find the nth term of the sequence, an? 5, 20, 80, 320, 1280, ...
an=4⋅5n−1
an=1.25⋅4n−1
an=5⋅4n−1
an=4⋅1.25n−1
Answers
Answer:
C.) 5 * 4^n-1
Step-by-step explanation:
Use the given method you use for finding the sequence with the terms.
Also K12 moment.
If it's wrong, please forgive me, I'm in the middle of the test as well.
I checked and I'm 99% sure this is the answer
Hope this helped despite being a little late!
A certain plane is described by 2x+3y+4z=16. Find the unit vector normal to the surface in the direction away from the origin.
Answers
A certain plane is described by 2x+3y+4z=16. Find the unit vector normal to the surface in the direction away from the origin.Firstly, we will obtain the coefficients of the x, y and z variables from the equation of the plane:2x + 3y + 4z = 16The coefficients are 2, 3, and 4 respectively.
Now, we will calculate the magnitude of the normal vector, ||N||, using the formula:||N|| = √(a² + b² + c²)where a, b, and c are the coefficients of the x, y, and z variables respectively.||N|| = √(2² + 3² + 4²)= √(4 + 9 + 16)= √29Therefore, the unit normal vector in the direction away from the origin is given by:N = (2/√29) i + (3/√29) j + (4/√29) k. Given the equation of a plane as 2x + 3y + 4z = 16, we have to find the unit vector normal to the surface in the direction away from the origin. Here's how we can do it:To find the unit vector normal to the surface, we first need to find the coefficients of the x, y, and z variables from the equation of the plane. In this case, the coefficients are 2, 3, and 4 respectively.Next, we can use the formula ||N|| = √(a² + b² + c²) to calculate the magnitude of the normal vector, where a, b, and c are the coefficients of the x, y, and z variables respectively. In this case, ||N|| = √(2² + 3² + 4²) = √29.Finally, we can find the unit normal vector in the direction away from the origin by dividing each coefficient by the magnitude of the normal vector, ||N||. Thus, the unit normal vector is:N = (2/√29) i + (3/√29) j + (4/√29) k
Therefore, the unit vector normal to the surface in the direction away from the origin is (2/√29) i + (3/√29) j + (4/√29) k.
To learn more about unit vector normal visit:
brainly.com/question/30895179
#SPJ11
For a result to be considered _____, the chances of its occurring as a result of random error are often less than 5 percent.
Answers
For a result to be considered significant, the chances of its occurring as a result of random error are often less than 5 percent.
What is Random error?A coincidental discrepancy between the observed and true values of anything is known as a random error (e.g., a researcher misreading a weighing scale records an incorrect measurement).
It's not always a mistake when there is random error; rather, it happens when measurements are made. Even when you measure the same item repeatedly, there will always be some variation in your results because to changes in the environment, the instrument, or your own perceptions.
Your measurements are equally likely to be greater or lower than the genuine values due to random error, which has unexpected effects.
According to the given data,
For a result to be considered significant, the chances of its occurring as a result of random error are often less than 5 percent.
To know more about Random error,visit;
https://brainly.com/question/14149934
#SPJ1
What is equidistant from a fixed point?
Answers
A set of points equidistant from a fixed point in a plane figure is called a circle where the distance between each of the set of the points and the fixed point forms the radius of the circle.
A point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal.
In two-dimensional Euclidean geometry, the locus of points equidistant from two given (different) points is their perpendicular bisector. In three dimensions, the locus of points equidistant from two given points is a plane, and generalising further, in n-dimensional space the locus of points equidistant from two points in n-space is an (n−1)-space.
Learn more about equidistant to visit this https://brainly.com/question/29634493
#SPJ4
help me out man i’ll give a crown to the smart one

Answers
Answer:
angle 4
its on the outside and it is alternate
Answer:
d
Step-by-step explanation:
Work out the area of this semicircle take pie to be 3.142 and write down all the digits given by your calculator 18cm
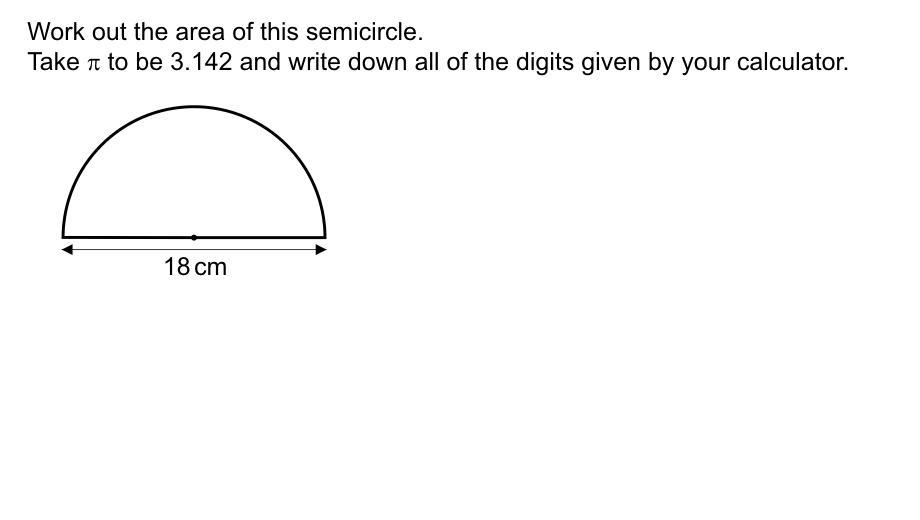
Answers
The area of the semi-circle with a diameter of 18 cm will be 127.17 square cm.
What is the area of the circle?It is the close curve of an equidistant point drawn from the center. The radius of a circle is the distance between the center and the circumference.
Let 'd' be the diameter of the circle. Then the area of the circle will be
A = (π/4)d² square units
The diameter is 18 cm. Then the area of the circle is given as,
A = (π/4) x 18²
A = (3.14 / 4) x 324
A = 254.34 square cm
Then the area of the semicircle is the area of the half of the circle, then we have
Semicircle area = 254.34 / 2
Semicircle area = 127.17 square cm
The area of the semi-circle with a diameter of 18 cm will be 127.17 square cm.
More about the area of a circle link is given below.
https://brainly.com/question/11952845
#SPJ1
I really need urgent help.
Y is between X and Z, XY = 6.9, and YZ = 14.8. Find XZ.
XZ = 7.9
XZ = 29.6
XZ = 20.7
XZ = 21.7
Answers
Answer:
21.7
Step-by-step explanation:
XZ=XY+YZ=6.9+14.8=21.7
Hope, this helps you.
What is the square root of 3 to the square root of 2 power times the square root of 3 to the negative square root of 2 power
Answers
Answer:
3
Step-by-step explanation:
multiplication rule of exponents is to multiply the bases (sq rt 3) and add the exponents
(sq rt 3)^2 = 3
add exponents and power of 1
If a line passes through (6,4) and (12,7), what is the slope? I really need help and if you can please explain how you got the asnwer
Answers
Answer:
0.5 OR 1/2
Step-by-step explanation:
Since the two points are (6,4) and (12,7) you would find the distance in x and y.
Slope = change in y/ change in x
Change in y: the y coordinates are 4 and 7, so 4 + 3 = 7. +3 is the change.
Change in x: the x coordinates are 6 and 12, so 6 + 6 = 12. +6 is the change.
Slope = 3/6 = 1/2 = 0.5 = 50%
Hope this helps :D
How to convert 1 million seconds to hours
Answers
Solution
Step 1
To convert seconds to hours, divide the seconds by 3600.
Step 2
1 million seconds = 1000000 seconds
\(\begin{gathered} To\text{ hours} \\ \\ \text{= }\frac{1000000}{3600} \\ \\ =\text{ }277\frac{7}{9}\text{ hours} \end{gathered}\)PLEASE HELP ME OUT. THANKS!
A circular pool has a diameter of 30 feet. A section of the top railing with a central angle of 27° is broken and needs to be replaced. What approximate length of railing needs to be replaced? Round your answer to one decimal place.
About ____ feet of railing needs to be replaced.
Answers
Using the circumference of the circle, it is found that:
About 7.1 feet of railing needs to be replaced.
What is the circumference of a circle?The circumference of a circle of radius r is given by:
\(C = 2\pi r\)
It is equivalent to 360º.
In this problem, the diameter is of 30 feet, hence the radius is 15 feet, so:
\(C = 2\pi (15) = 30\pi\)
Then, considering that the circumference is equivalent to 360º, the length to be replaced is given by:
\(L = \frac{27}{360} \times 30\pi = 7.1\)
About 7.1 feet of railing needs to be replaced.
More can be learned about the circumference of a circle at https://brainly.com/question/25846963
Answer: 7.1
Step-by-step explanation: ANSWER ON EDMENTUM/PLUTO

Identify the segments that are parallel, if any, if ∠EDA≅∠HCB.
Answers
In the above question, (image attached) The option that shows the segments that are parallel, if any, if ∠EDA≅∠HCB is option A: None of these.
What is the line segment about?Note that by examining the the image if ∠EDA≅∠HCB, the two lines can never intersect even if they go a longer distance.
The reason why is that there are no parallel lines on it and as such, they cannot intercept.
Hence, In the above question, (image attached) The option that shows the segments that are parallel, if any, if ∠EDA≅∠HCB is option A: None of these.
Learn more about Line segments from
https://brainly.com/question/2437195
#SPJ1

The graph of y=2x^2-4x+2 has an y-intercept of (0,2).
True or false?
Answers
Answer:
True, there is a y-intercept at (0,2)

Tell whether the figure has line symmetry. If so how many lines of symmetry are there?

Answers
**NEED THIS WITHIN 5 MINS** Stan’s employer pays for 45% of his annual health insurance premium of $4,567.00. Stan pays the remaining balance by having it deducted in equal amounts from his 26 paychecks throughout the calendar year. How much will Stan have deducted from each paycheck?
Answers
Answer:
$88.3
Step-by-step explanation:
Here 42% of annual health premium($5450)=*5450
=$2289
This amount is being paid by the company means it is deducted amount in one year.
One year has 26 paychecks so above amount divided by 26 is rebate amount in each paycheck.
Deducted amount=
=$88.30
Find the orthogonal decomposition of v with respect to w. v = 1-1 , w = span| | 2 | , 2 projw(v)- | | | perpw(v) = Read It TII ( Talk to a Tutor l
Answers
The orthogonal decomposition of v with respect to w is [1, -1].
How to find the orthogonal decomposition of v with respect to w?To find the orthogonal decomposition of v with respect to w, we need to find the orthogonal projection of v onto w, and the projection of v onto the orthogonal complement of w.
First, let's find the orthogonal projection of v onto w. The formula for the orthogonal projection of v onto w is:
\(\proj w(v) = ((v \cdot w)/||w||^2) * w\)
where · represents the dot product and ||w|| represents the magnitude of w.
We have:
v = [1, -1]
w = [2, 2]
The dot product of v and w is:
v · w = 1*2 + (-1)*2 = 0
The magnitude of w is:
\(||w|| = \sqrt(2^2 + 2^2) = 2\sqrt(2)\)
Therefore, the orthogonal projection of v onto w is:
\(\proj w(v) = ((v \cdot w)/||w||^2) * w = (0/(2\sqrt(2))^2) * [2, 2] = [0, 0]\)
Next, let's find the projection of v onto the orthogonal complement of w. The orthogonal complement of w is the set of all vectors that are orthogonal to w.
We can find a basis for the orthogonal complement of w by solving the equation:
w · x = 0
where x is a vector in the orthogonal complement. This equation represents the condition that x is orthogonal to w.
We have:
w · x = [2, 2] · [x1, x2] = 2x1 + 2x2 = 0
Solving this equation for x2, we get:
x2 = -x1
So any vector of the form [x1, -x1] is in the orthogonal complement of w. Let's choose [1, -1] as a basis vector for the orthogonal complement.
To find the projection of v onto [1, -1], we can use the formula:
\(\proj u(v) = ((v \cdot u)/||u||^2) * u\)
where u is a unit vector in the direction of [1, -1]. We can normalize [1, -1] to obtain:
\(u = [1, -1]/||[1, -1]|| = [1/\sqrt(2), -1/\sqrt(2)]\)
The dot product of v and u is:
\(v \cdot u = 1*(1/\sqrt(2)) - 1*(-1/\sqrt(2)) = \sqrt(2)\)
The magnitude of u is:
\(||u|| = \sqrt((1/\sqrt(2))^2 + (-1/\sqrt(2))^2) = 1\)
Therefore, the projection of v onto [1, -1] is:
\(\proj u(v) = ((v \cdot u)/||u||^2) * u = (\sqrt(2)/1^2) * [1/\sqrt(2), -1/\sqrt(2)] = [1, -1]\)
Finally, the orthogonal decomposition of v with respect to w is:
v =\(\proj w(v) + \proj u(v)\) = [0, 0] + [1, -1] = [1, -1]
Therefore, the orthogonal decomposition of v with respect to w is [1, -1].
Learn more about orthogonal decomposition
brainly.com/question/30453255
#SPJ11
How much storage is needed to represent a simple graph with n vertices and m edges using
a) adjacency lists?
b) an adjacency matrix?
c) an incidence matrix?
Answers
The amount of storage required to represent a simple graph with n vertices and m edges can vary depending on the chosen representation. Here's the storage requirement for each representation:
a) Adjacency lists:
In an adjacency list representation, we typically use an array of size n to store the vertices, and for each vertex, we maintain a linked list or an array to store its adjacent vertices. The space complexity of this representation is O(n + m), where n is the number of vertices and m is the number of edges.
Each vertex requires constant space, and each edge is represented by a link or entry in the adjacency list.
b) Adjacency matrix:
In an adjacency matrix representation, we use a 2D matrix of size n x n to represent the graph. Each entry (i, j) in the matrix represents whether there is an edge between vertices i and j. The space complexity of this representation is O(n^2), as we need to store n^2 entries for the complete matrix. However, if the graph is sparse (few edges compared to vertices), the space complexity can be reduced to O(n + m) by only storing the entries corresponding to the existing edges.
c) Incidence matrix:
In an incidence matrix representation, we use a 2D matrix of size n x m, where n is the number of vertices and m is the number of edges. Each entry (i, j) in the matrix represents whether vertex i is incident to edge j. The space complexity of this representation is O(n * m), as we need to store n * m entries for the matrix.
Similar to the adjacency matrix, if the graph is sparse, the space complexity can be reduced to O(n + m) by storing only the entries corresponding to the existing edges.
In summary:
a) Adjacency lists: O(n + m)
b) Adjacency matrix: O(n^2) or O(n + m) for sparse graphs
c) Incidence matrix: O(n * m) or O(n + m) for sparse graphs
To know more about matrix refer here:
https://brainly.com/question/28180105?#
#SPJ11
Jackie runs and dances for 75 minutes every day.
She dances 25 minutes more than she runs.
Part A: Write a pair of linear equations to show the relationship between the number of minutes
runs (x) and the number of minutes she dances (y) every day.
Part B: How much time does Jackie spend running every day? Show your work.
Part C: What is the greatest amount of time she could spend dancing every day, given she will take a
run.
Explain your reasoning.
PLEASE HELP DUE SOON!
Answers
Answer:
A. y = x + 25
x + y = 75
B. 25 minutes
C. 50 minutes
Step-by-step explanation:
Define the variables:
Let x = the number of minutes Jackie runs every day.Let y = the number of minutes Jackie dances every day.Part AIf Jackie dances 25 minutes more than she runs:
\(\implies y=x+25\)
If Jackie runs and dances for 75 minutes:
\(\implies x+y=75\)
Part BSubstitute the first equation into the second equation and solve for x:
\(\implies x+(x+25)=75\)
\(\implies 2x+25=75\)
\(\implies 2x+25-25=75-25\)
\(\implies 2x=50\)
\(\implies 2x\div 2=50 \div 2\)
\(\implies x=25\)
Therefore, Jackie spends 25 minutes running everyday.
Part CSubstitute the found value of x into the first equation and solve for y:
\(\implies y=25+25\)
\(\implies y=50\)
Therefore, the greatest amount of time Jackie could spend dancing every day, given she will take a run, is 50 minutes.
