Answers
Answer:
i think it is c or d
Step-by-step explanation:
Related Questions
Liz flips a coin 80 times. The coin lands heads up 32 times and tails up 48 times. Complete each statement. The theoretical probability of the coin landing heads up is 50%. (Type an integer or a decimal.) Based on Liz's results, the experimental probability of the coin landing heads up is
Answers
Answer:
40%
Step-by-step explanation:
Answer: 50, 60, Less.
Step-by-step explanation: The theoretical probability of the coin landing heads up is 50%
Based on Liz's results, the experimental probability of the coin landing heads up is 60
The theoretical probability is less than the experimental probability in this experiment.
Hope this helped have a nice day!
A nutrition researcher wants to determine the mean fat content of hen's eggs. She collects a sample of 40 eggs. She calculates a mean fat content of 23 grams with a sample standard deviation of 8 grams. From these statistics, she calculates a 90% confidence interval of 20.9 grams to 25.1 grams. What can the researcher do to decrease the width of the confidence interval?
a. increase the confidence level
b. decrease the confidence level
c. decrease the sample size
d. none of the above
Answers
To decrease the width of the confidence interval, the researcher can take the following steps:
1. Decrease the confidence level: The confidence interval width is inversely proportional to the confidence level. By decreasing the confidence level, the researcher can have a narrower interval. However, it is important to note that decreasing the confidence level also increases the chance of the interval not capturing the true population mean.
2. Increase the sample size: The sample size affects the precision of the estimate. Increasing the sample size reduces the standard error, which leads to a narrower confidence interval. This is because a larger sample provides more information about the population.
Therefore, the researcher can decrease the width of the confidence interval by either decreasing the confidence level or increasing the sample size. Both approaches will result in a narrower interval, providing a more precise estimate of the mean fat content of hen's eggs.
The researcher can decrease the width of the confidence interval by either decreasing the confidence level or increasing the sample size. Both approaches will result in a more precise estimate of the mean fat content of hen's eggs.
To know more about proportional , visit ;
https://brainly.com/question/33460130
#SPJ11
Georgia bought a pair of flip-flops that cost $3.46 and a pair of slip-on shoes that cost $9.87.
She paid a total of $ for the two pairs of shoes.
Answers
Answer: The cost for the two pairs of shoes is $13.33
Step-by-step explanation:
Since we have given that
Cost of pair of flip flops = $3.46
Cost of pair of slip on shoes = $9.87
We need to find the cost of two pairs of shoes.
Cost of two pairs of shoes = Cost of pair of flip flops + Cost of pair of slip on shoes
\(cost=3.46+9.87=13.33\)
the cost for the two pairs of shoes is $13.33.
What is it? Could someone draw these coordinates

Answers
The coordinates are simple. Hope you understand this and you can draw it out.

19 + 1.5(10m – 8) = 127
Answers
\(19+1,5(10m-8)=127\\\\19+15m-12=127\\\\15m+7=127 \ \ /-7\\\\15m=120 \ \ /:15\\\\\huge\boxed{m=8}\)
Answer:
\(m=8\)
Step-by-step explanation:
\(19 + 1.5(10m-8) = 127\)
Multiply both sides by 10
\(190+15(10m-8)=1270\)
Subtract 190 from both sides
\(15(10m-8)=1080\)
Divide both sides by 15
\(10m-8=72\)
Add 8 to both sides
\(10m=80\)
Simplify
\(m=8\)
Exercise 6.3.9: Write down the solution to x'' - 2x = e^(-t^2) , x(0) = 0, x'(0) = 0 as a definite integral.
Hint: Do not try to compute the Laplace transform of e??t2 .
Answers
The solution of the original equation with the given initial conditions is:
x(t) = ∫-e^(-t^2 - √2t)/2 dt * e^(√2t) + ∫e^(-t^2 + √2t)/2 dt * e^(-√2t)
The solution to the differential equation x'' - 2x = e^(-t^2) with the initial conditions x(0) = 0 and x'(0) = 0 can be found by using the method of variation of parameters. First, we need to find the general solution of the homogeneous equation x'' - 2x = 0. The characteristic equation is r^2 - 2 = 0, which has two real and distinct roots r1 = √2 and r2 = -√2. Therefore, the general solution of the homogeneous equation is xh(t) = c1e^(√2t) + c2e^(-√2t).
Now, we need to find a particular solution xp(t) of the non-homogeneous equation. We can use the method of variation of parameters and assume that xp(t) = u1(t)e^(√2t) + u2(t)e^(-√2t). Taking the first and second derivatives of xp(t) and substituting them into the original equation, we get:
u1'(t)e^(√2t) + u2'(t)e^(-√2t) = 0
u1''(t)e^(√2t) - 2u1'(t)e^(√2t) + u2''(t)e^(-√2t) + 2u2'(t)e^(-√2t) = e^(-t^2)
Solving this system of equations for u1'(t) and u2'(t), we get:
u1'(t) = -e^(-t^2 - √2t)/2
u2'(t) = e^(-t^2 + √2t)/2
Integrating both sides of these equations, we get:
u1(t) = ∫-e^(-t^2 - √2t)/2 dt
u2(t) = ∫e^(-t^2 + √2t)/2 dt
Substituting these expressions back into the formula for xp(t), we get:
xp(t) = ∫-e^(-t^2 - √2t)/2 dt * e^(√2t) + ∫e^(-t^2 + √2t)/2 dt * e^(-√2t)
Finally, the general solution of the original equation is x(t) = xh(t) + xp(t) = c1e^(√2t) + c2e^(-√2t) + ∫-e^(-t^2 - √2t)/2 dt * e^(√2t) + ∫e^(-t^2 + √2t)/2 dt * e^(-√2t).
Using the initial conditions x(0) = 0 and x'(0) = 0, we can find the values of c1 and c2:
0 = c1 + c2
0 = √2c1 - √2c2
Solving this system of equations, we get c1 = c2 = 0. Therefore, the solution of the original equation with the given initial conditions is:
x(t) = ∫-e^(-t^2 - √2t)/2 dt * e^(√2t) + ∫e^(-t^2 + √2t)/2 dt * e^(-√2t)
This is the solution to the differential equation x'' - 2x = e^(-t^2) with the initial conditions x(0) = 0 and x'(0) = 0 as a definite integral.
For more similar questions on Laplace:
brainly.com/question/28167783
#SPJ11
The Land of Nod lies in the monsoon zone, and has just two seasons, Wet and Dry. The Wet season lasts for 1/3 of the year, and the Dry season for 2/3 of the year. During the Wet season, the probability that it is raining is 3/4; during the Dry season, the probability that it is raining is 1/6. (a) I visit the capital city, Oneirabad, on a random day of the year. What is the probability that it is raining when I arrive? (b) I visit Oneirabad on a random day, and it is raining when I arrive. Given this information, what is the probability that my visit is during the Wet season? (c) I visit Oneirabad on a random day, and it is raining when I arrive. Given this information, what is the probability that it will be raining when I return to Oneirabad in a year's time? (You may assume that in a year's time the season will be the same as today but, given the season, whether or not it is raining is independent of today's weather.)
Answers
Answer:
Step-by-step explanation:
(a) To find the probability that it is raining when you arrive in Oneirabad on a random day, we need to use the law of total probability.
Let A be the event that it is raining, and B be the event that it is the Wet season.
P(A) = P(A|B)P(B) + P(A|B')P(B')
Given that the Wet season lasts for 1/3 of the year, we have P(B) = 1/3. The probability that it is raining during the Wet season is 3/4, so P(A|B) = 3/4.
The Dry season lasts for 2/3 of the year, so P(B') = 2/3. The probability that it is raining during the Dry season is 1/6, so P(A|B') = 1/6.
Now we can calculate the probability that it is raining when you arrive:
P(A) = (3/4)(1/3) + (1/6)(2/3)
= 1/4 + 1/9
= 9/36 + 4/36
= 13/36
Therefore, the probability that it is raining when you arrive in Oneirabad on a random day is 13/36.
(b) Given that it is raining when you arrive, we can use Bayes' theorem to calculate the probability that your visit is during the Wet season.
Let C be the event that your visit is during the Wet season.
P(C|A) = (P(A|C)P(C)) / P(A)
We already know that P(A) = 13/36. The probability that it is raining during the Wet season is 3/4, so P(A|C) = 3/4. The Wet season lasts for 1/3 of the year, so P(C) = 1/3.
Now we can calculate the probability that your visit is during the Wet season:
P(C|A) = (3/4)(1/3) / (13/36)
= 1/4 / (13/36)
= 9/52
Therefore, given that it is raining when you arrive, the probability that your visit is during the Wet season is 9/52.
(c) Given that it is raining when you arrive, the probability that it will be raining when you return to Oneirabad in a year's time depends on the season. If you arrived during the Wet season, the probability of rain will be different from if you arrived during the Dry season.
Let D be the event that it is raining when you return.
If you arrived during the Wet season, the probability of rain when you return is the same as the probability of rain during the Wet season, which is 3/4.
If you arrived during the Dry season, the probability of rain when you return is the same as the probability of rain during the Dry season, which is 1/6.
Since the season you arrived in is independent of the weather when you return, we need to consider the probabilities based on the season you arrived.
Let C' be the event that your visit is during the Dry season.
P(D) = P(D|C)P(C) + P(D|C')P(C')
Since P(C) = 1/3 and P(C') = 2/3, we can calculate:
P(D) = (3/4)(1/3) + (1/6)(2/3)
= 1/4 + 1/9
= 9/36 + 4/36
= 13/36
Therefore, the probability that it will be raining when you return to Oneirabad in a year's time, given that it is raining when you arrive, is 13/36.
To know more about probability refer here:
https://brainly.com/question/32117953
#SPJ11
two containers are used to hold liquid. these containers have exactly the same shape. the first container has a height of 12 m, and it can hold 48 m^3 of liquid. if the second container has a height of 30 m, how much liquid can it hold?
Answers
If the second container has a height of 30 m, the second container can hold 300 m³ of liquid.
Since the two containers have exactly the same shape, their volumes are proportional to the cubes of their corresponding dimensions. Let's denote the volume of the second container as V₂ and its height as h₂. Then we have:
(V₂ / V₁) = (h₂ / h₁)³
where V₁ and h₁ are the volume and height of the first container, respectively. Substituting the given values, we get:
(V₂ / 48) = (30 / 12)³
(V₂ / 48) = 2.5³
V₂ = 48 × 2.5³
V₂ = 300 m³
Therefore, the second container can hold 300 m³ of liquid.
For more details regarding volume, visit:
https://brainly.com/question/1578538
#SPJ1
Write a whole number and a fraction greater than 1 to name the part filled. Think 1 container = 1.
Answers
\(\huge \boxed{Answer}\)
there are two containers in four parts has to be filled in each, therefore, the fraction greater than one will be =
total number of part stobe filler in container
_________________________________________
number of parts in each container
= 8/4
the whole number greater than one will be = 2
hence, the whole number and a fraction greater than one to name the part filled is 2 and 8/4
plzzzzz help need to turn this in by tonight

Answers
Answer:
A=17
Step-by-step explanation:
Find 20 rational numbers between -3/7 and 2/3
Answers
The 20 rational numbers between -3/7 and 2/3 are: -0.42857, -0.14286, 0.14286, 0.42857, 0.71429, -0.28571, -0.07143, 0.07143, 0.28571, 0.57143, -0.61538, -0.38462, -0.15385, 0.15385, 0.38462, 0.61538, -0.5, -0.25, 0.25, 0.5.
Rational numbers are numbers that can be expressed as a ratio of two integers, where the denominator is not equal to zero. In other words, any number that can be written in the form of a fraction a/b, where a and b are integers and b is not equal to zero, is a rational number.
To find 20 rational numbers between -3/7 and 2/3, we need to find the difference between 2/3 and -3/7, which is 65/21. Then we divide 65/21 by 21 to get the increment value of 3/7. Starting with -3/7, we add 3/7 to it 20 times to get the 20 rational numbers between -3/7 and 2/3.
To know more about rational numbers, here
brainly.com/question/29365428
#SPJ4
\((\frac{8a^{-5}b^{4} }{12a^{-6}b^{-2} })\)
Answers
Answer:
\(→ \frac{8 {a}^{( - 5) } {b}^{(4)} }{12 {a}^{( - 6)} {b}^{( - 2)} } = \frac{2 {a}^{(6 - 5)}{b}^{(4 + 2)} }{3} = \boxed{ \frac{2}{3}a {b}^{6} }✓ \\ \)
(2/3)ab⁶ is the right answer.Solve the equation.
1. For parentheses:
Distribute
6.8x+9.3 = -9.4+3.4(2-5x)
2. If necessary:
Combine Terms
3. Apply properties:
Add
Subtract
Multiply
Divide
4. To start over:
Reset
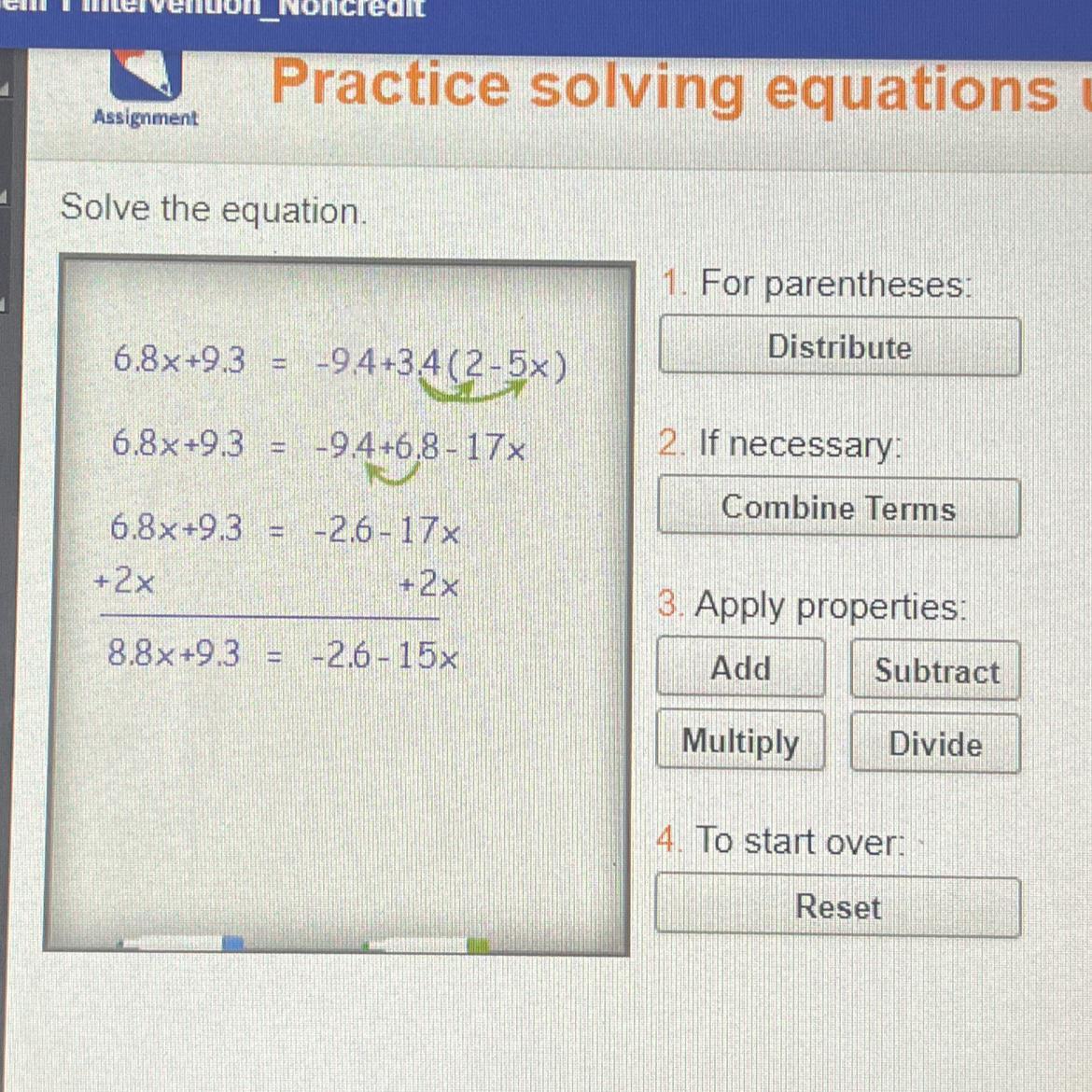
Answers
Equations can have zero, one or more solutions
The solution to the equation is x = -0.5
The equation is given as:
\(6.8x+9.3 = -9.4+3.4(2-5x)\)
Distribute the expression
\(6.8x+9.3 = -9.4+3.4\times 2-3.4\times 5x\)
\(6.8x+9.3 = -9.4+6.8-17x\)
Apply addition properties
\(6.8x+9.3 = -2.6-17x\)
Combine terms
\(6.8x+17x =-9.3 -2.6\)
Apply addition properties
\(23.8x =-11.9\)
Apply division properties
\(x =-0.5\)
Hence, the solution to the equation is -0.5
Read more about equations at:
https://brainly.com/question/13136492
PLEASE HELP ME WITH THIS ASAP, I’m really confused.

Answers
Answer:
scalene triangle for the first
equilateral triangle for the second
isosceles triangle for the 3rd
Answer:
The first is a scalene triangle. No two sides on a scalene trinagle will have the same length.
The second is an equilateral triangle. Equilateral literally means "equal sides".
The third is an isosceles triangle. These triangle will have perfect symmetry.
140 is what percent
less than 160 ? PLSASE HELP
Answers
Answer:
The answer should be 12.5%
i need to find the product

Answers
Answer:
c ik this because I took the same question as you
The product of the given algebraic expression is \(\frac{4}{(x-1)}\).
The given expression is \(\frac{8x+8}{x^2-2x+1} .\frac{x-1}{2x+2}\).
Multiplication is an operation that represents the basic idea of repeated addition of the same number. The numbers that are multiplied are called the factors and the result that is obtained after the multiplication of two or more numbers is known as the product of those numbers.
Here, \(\frac{4(2x+2)}{x^2-1x-1x+1} \times \frac{x-1}{2x+2}\)
= \(\frac{4(2x+2)}{x(x-1)-1(x-1)} \times \frac{x-1}{2x+2}\)
= \(\frac{4(2x+2)}{(x-1)(x-1)} \times \frac{x-1}{2x+2}\)
Cancel the same factors, that is
= \(\frac{4}{(x-1)} \times \frac{1}{1}\)
= \(\frac{4}{(x-1)}\)
Therefore, the product of the given algebraic expression is \(\frac{4}{(x-1)}\).
Learn more about the multiplication here:
https://brainly.com/question/1562995.
#SPJ6
a spinner with 8 numbers is spun. the numbers on the spinner are: 7, 4, 8, 7, 8, 8, 2, and 8. what is the expected value of a single spin?
Answers
The expected value of a single spin would be number 8 because it the the most occuring number of the spinner.
How to determine the expected value from a data set?To determine the expected value, the most occuring value should be identified which is equally the mode of the data set.
Of all the numbers in the spinner, the most occuring data is number 8 which appeared 4 times.
Therefore, the expected value as a spin should be number 8.
Learn more about probability here:
https://brainly.com/question/31123570
#SPJ4
What is the difference between a factor of a number and a multiple of a number? use the number 25 has an example
Answers
Answer:
factor: a submultiple; an integer value that gives an integer quotient when the number is divided by it.multiple: the product of the number and another integerStep-by-step explanation:
FactorsA set of factors of a number (N) is a set of integers {f1, f2, f3, ...} whose product is the number:
f1 × f2 × f3 × ... = N
Often the term "factors" is used to mean "prime factors," the set of prime numbers whose product is N.
When N = 25, the prime factors are {5, 5}. That is ...
5×5 = 25
__
DivisorsA "divisor" of a number is a sub-multiple of N. That is, the quotient N/k is an integer for some divisor k of N. Usually, we're interested in integer divisors. All prime factors will be integer divisors of N. The term "factor" is often used when the term "divisor" is meant.
Divisors of N = 25 include 1, 5, and 25. There will be an odd number of integer divisors (as here) if the number N is a perfect square.
__
MultiplesFor an integer k, the value k×N is called a multiple of N, often, the k-th multiple of N.
Multiples of 25 include 25, 50, 75, 100, 125, and any other decimal number ending in 25, 50, 75, or 00.
__
Another example
When N=30, the prime factors are {2, 3, 5}. The divisors are {1, 2, 3, 5, 6, 10, 15, 30}. (Note there are an even number of divisors.) Multiples of 30 include 30, 60, 90, 120, ....
Write the equation of the line in Point-Slope form
that has a slope of 1/3 and passes through the point (6,1)
Answers
Answer: \(y-1=\frac{1}{3} (x-6)\)
Point slope form is: \(y-y_{1} = m (x-x_{1} )\), where m=slope and y1 & x1 is the point given. So plug the slope 1/3 and point (6,1) into the spots to make it into point slope form.
a bus drives for 3 and a half hours at an average speed of 56mph how far does the bus drive?
Answers
Answer:
196 miles
Step-by-step explanation:
distance (D) is calculated as
D = S × T ( S is average speed and T is time in hours )
here T = 3 and a half hours = 3.5 hours and S = 56 , then
D = 56 × 3.5 = 196 miles
Domain and rang of these

Answers
Answer:
Domain: {-3, -1, 1}
Range: {-1, 2, 4, 5}
Step-by-step explanation:
The domain is all the x-values, and the range is all the y-values. When listing values, repeated values are only written down once.
A vector has a magnitude of 15
and a direction of 210°. What
are its horizontal and vertical
components?
([?], [
Round to the nearest hundredth.
![A vector has a magnitude of 15and a direction of 210. Whatare its horizontal and verticalcomponents?([?],](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/e5yNhc4Zqb40kYHNGlFQ3Z999bKpAP4m.png)
Answers
The magnitude of the vector of 15 units and the vector direction of 210° indicates that the horizontal and vertical components of the vector are;
(-12.99, -7.5)
What are the formula for finding the components of a vector?The horizontal and vertical component of the vector can be found from the following formula;
Horizontal component = Magnitude × cos(direction angle)
Vertical component = Magnitude × sin(direction angle)
The magnitude of the vector = 15
The direction (angle) of the vector = 210°
Therefore; Horizontal component = 15 × cos(210°) ≈ -12.99Vertical component = 15 × sin(210°) = -7.5Learn more on the components of a vector here: https://brainly.com/question/24855749
#SPJ1
how many 8-place license plates with 5 letters and 3 digits are possible if the only restriction is that all letters and numbers are unique? what if the 3 digits must be consecutive in the string?
Answers
For the first part, the number of license plates is: 65,780,800 and for the second part, the number of license plates with 3 consecutive digits is: 16,524,288.
How did we get these values?If there are no restrictions on where the digits and letters are placed, the number of 8-place license plates consisting of 5 letters and 3 digits with no repetitions allowed can be found using the permutation formula:
nPr = n! / (n-r)!
where n is the number of available characters (26 letters and 10 digits) and r is the number of characters needed for the license plate (8).
Therefore, the number of license plates is:
(26 P 5) x (10 P 3) = (26!/21!) x (10!/7!) = 65,780,800
If the 3 digits must be consecutive, there are 8 possible positions for the block of digits (either the first 3, second 3, or last 3). Once the position of the block is chosen, the number of license plates can be found by counting the number of ways to arrange the letters and the block of digits. The number of ways to arrange the letters is 26 P 5, and the number of ways to arrange the block of digits is 10 (since there are only 10 possible sets of consecutive digits).
Therefore, the number of license plates with 3 consecutive digits is:
8 x (26 P 5) x 10 = 16,524,288
learn more about permutation formula: https://brainly.com/question/1216161
#SPJ1
The complete question goes thus:
If there are no restrictions on where the digits and letters are placed, how many 8
-place license plates consisting of 5
letters and 3
digits are possible if no repetitions of letters or digits are allowed? What if the 3
digits must be consecutive?
Shelby made equal deposits at the beginning of every 3 months into an RRSP. At the end of 9 years, the fund had an accumulated value of $55,000. If the RRSP was earning 3.50\% compounded monthly, what was the size of the quarterly deposits? Round to the nearest cent
Answers
The size of the quarterly deposits in Shelby's RRSP account was approximately $147.40.
Let's denote the size of the quarterly deposits as \(D\). The total number of deposits made over 9 years is \(9 \times 4 = 36\) since there are 4 quarters in a year. The interest rate per period is \(r = \frac{3.50}{100 \times 12} = 0.0029167\) (3.50% annual rate compounded monthly).
Using the formula for the future value of an ordinary annuity, we can calculate the accumulated value of the RRSP fund:
\[55,000 = D \times \left(\frac{{(1 + r)^{36} - 1}}{r}\right)\]
Simplifying the equation and solving for \(D\), we find:
\[D = \frac{55,000 \times r}{(1 + r)^{36} - 1}\]
Substituting the values into the formula, we get:
\[D = \frac{55,000 \times 0.0029167}{(1 + 0.0029167)^{36} - 1} \approx 147.40\]
Therefore, the size of the quarterly deposits, rounded to the nearest cent, is approximately $147.40.
To learn more about interest Click Here: brainly.com/question/30393144
#SPJ11
Which statement is true about the angle bisector AD of △ABC?
Answers
Theorems are statements or propositions in mathematics that have been proven to be true based on logical reasoning or mathematical proof.
There are some general properties and theorems related to angle bisectors that can be considered:
Angle Bisector Theorem: The angle bisector of an angle in a triangle divides the opposite side into segments that are proportional to the adjacent sides. In other words, if AD is the angle bisector of ∠BAC, then BD/DC = AB/AC.
Concurrency of Angle Bisectors: In any triangle, the angle bisectors of the three angles are concurrent, meaning they intersect at a single point called the incenter. This point is equidistant from the sides of the triangle.
Equal Angles: The angle bisector divides an angle into two equal angles. In other words, if AD is the angle bisector of ∠BAC, then ∠BAD = ∠DAC.
Internal and External Angle Bisectors: An angle bisector can be internal or external to the triangle, depending on its position. Internal angle bisectors intersect within the triangle, while external angle bisectors extend outside the triangle.
These are some general statements and properties associated with angle bisectors.
To learn more about Bisectors visit;
https://brainly.com/question/19023272
#SPJ11
In 1895, the first U.S. Open Goif Championship was held. The winner's prize money was $150, In 2016 , the winner's check was $2.3 million. What was the percentage increase per year in the winner's check over this period? foo not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e,9. 32.16.)
Answers
Rounded to two decimal places, the percentage increase per year in the winner's check over this period is approximately 15,332.33%.
To calculate the percentage increase per year in the winner's check over the period from 1895 to 2016, we can use the following formula:
Percentage increase = [(Final value - Initial value) / Initial value] * 100
Initial value: $150
Final value: $2,300,000
Number of years: 2016 - 1895 = 121 years
Percentage increase = [(2,300,000 - 150) / 150] * 100
= (2,299,850 / 150) * 100
= 15,332.33%
Rounded to two decimal places, the percentage increase per year in the winner's check over this period is approximately 15,332.33%.
Learn more about percentage here:
https://brainly.com/question/24877689
#SPJ11
The volume of a sphere whose diameter is 18 centimeters is _π cubic centimeters
Answers
Answer:
12 pi cubic cm
Step-by-step explanation:
The range for the Kentucky temperatures is . The range for the Illinois temperatures is . The IQR for the Kentucky temperatures is . The IQR for the Illinois temperatures is . The box plots show
Answers
The boxplot required to answer the questions is attached below :
Answer:
The range for the Kentucky temperature :
(58.3 - 52.2) = 6.1
The range for the Illinois temperature :
(55 - 49.9) = 5.1
The IQR for the Kentucky temperature :
(57.3 - 54.5) = 2.8
The IQR for the Illinois temperature :
(53.3 - 50.9) = 2.4
Step-by-step explanation:
Range = maximum - minimum
Maximum and minimum values are given by the values at the end and start of the whisker.
The range for the Kentucky temperature :
(58.3 - 52.2) = 6.1
The range for the Illinois temperature :
(55 - 49.9) = 5.1
IQR = Q3 - Q1
Q3 = Value at the end of the box
Q1 = value of start of box
The IQR for the Kentucky temperature :
(57.3 - 54.5) = 2.8
The IQR for the Illinois temperature :
(53.3 - 50.9) = 2.4

Answer:
The range for the Kentucky temperatures is ✔ 6.1
The range for the Illinois temperatures is ✔ 5.1
The IQR for the Kentucky temperatures is ✔ 2.8
The IQR for the Illinois temperatures is ✔ 2.4
The box plots show ✔ more variation for Kentucky
Step-by-step explanation:
I just did it and got it correct.

100 PTS!!!! The perimeter of a rectangle is 4(4x - 5) inches. the length of the sides of the rectangle are 2 x + 3 inches and 3x + 2 inches. WRITE AND SOLVE an EQUATION to find the length of each side of the rectangle. ( you have to show all work for branliest!!!!! :D)
Answers
Answer:
2 sides are \(\frac{33}{13}\) or 2.5
2 sides are \(\frac{47}{13}\) or 3.6
Step-by-step explanation:
There must be 2 2x+3s and 2 3x+2s
The perimeter is the sum of the sides (it has 4 sides)
2(2x+3) + 2(3x+2) = 4(4x-5)
distributive property
2*2x + 2*3
4x+6
other one
2*3x + 2*2
6x+4
perimeter
4*4x + 4*-5
16x-20
together...
(4x+6) + (6x+4) = 16x-20
add like terms
10x+10 = 16x-20
add 20 to both sides
10x+30 = 16x
subtract 10x from both sides
30 = 26x
divide by 26 on both sides
\(\frac{30}{26} = x\)
simplify
\(\frac{15}{13}\)
Substitute the x value
2 of the sides are 2x+3
so
\(2(\frac{15}{13} ) + 3\)
\(\frac{30}{13} + \frac{3}{1}\)
\(\frac{33}{13}\)
or 2.5
other sides
\(3(\frac{15}{13} ) + 2\)
\(\frac{45}{13} + \frac{2}{1}\)
\(\frac{47}{13}\) or 3.6
That's all I can say for now! Hope this helps and a thank won't hurt! :)
help me plz ok thank you

Answers
Answer:
If there is no 48 divided by 8 then it is 8 x _ = 48.
Step-by-step explanation:
Think about it. There are 6 times more children than adults *6 x 8 = 48.
Answer:
8 x______=48
Step-by-step explanation:
In the problem, they are telling you there are 48 children and 8 adults at the library. Then, they tell you how many times more adults than children are at the library. You aren't adding, and since they are saying times more, that is a sign of multiplication. Hope this helps!
