Answers
Answer:
Step-by-step explanation:
a) See attached picture
b) d=0.5(6)
= 3 - (6,3) --> Time is independent variable so it is the x value
c) 4=0.5t
x=8 --> (8,4)

Related Questions
How far is the train from its destination?
How long does the train travel when it finally reaches its destination? (Hint: when you reach your destination, that equals 0 miles? I need help

Answers
Your experiment is using a one-tailed test with an alpha level of .05. Your alternative hypothesis predicts an increase in test scores. The correct value of z crit for this test is ____________.
Answers
Answer:
The correct value of z crit for this test is +1.645
Step-by-step explanation:
Ski Lift A takes skiers 1,200 feet up the mountain in 2 minutes, Ski Lift B takes skiers 1,500 feet up the mountain in 3 minutes, and Ski Lift C takes skiers 1,800 feet up the mountain in 2 1⁄2 minutes. Which ski lift has the fastest rate?
Answers
Answer:
iek
Step-by-step explanation:3283349
In triangle ABC, ∠A is a right angle and m∠B = 45°. Find BC. If your answer is not an integer, leave it in the simplest radical form. The question is multiple choice and the choices are below. A. 20\(\sqrt{2}\) ft B. 10 ft C. 20 ft D. 10 \(\sqrt{2}\) ft

Answers
Answer: D \(10\sqrt{2}\)
Step-by-step explanation:
It says that the measure of angle B is 45 degrees. So if we were to put in 45 degrees we could see that is is opposite AC and BC which we needs to find is the hypotenuse. So since we know the opposite of angle B is 10 ft we can using that to find the length of BC. Opposite hypotenuse is the sine function so we will use it to calculate the length of BC.
sin(45) = \(\frac{10}{BC}\) multiply both sides by BC
BC sin(45) = 10 divide both sides by sin(45)
BC = \(\frac{10}{sin(45)}\)
BC = \(10\sqrt{2}\)
Answer:
\(\huge\boxed{Option\ D : \ BC = 10\sqrt{2}\ ft }\)
Step-by-step explanation:
Since it's a right angled triangle, We'll use trigonometric rations.
Given that m∠B = 45°
So,
Sin B = opposite / hypotenuse
Where m∠B = 45°, opposite = 10 ft and hypotenuse = BC
Sin 45 = 10 / BC
\(\sf \frac{\sqrt{2} }{2} = \frac{10}{BC}\)
BC = 20 / √2
Multiplying and Dividing by √2
BC = 20√2 / √(2)²
BC = 20 √2 / 2
BC = 10√2 ft
The ages of the people at two tables in a restaurant are shown in the chart. Which statement about the ranges of the data sets is true?
Answers
Answer:
Where is the data ?
Step-by-step explanation:
Need the data set
Determine the value of the 10% trimmed mean. (Round your answer to four decimal places.)
0.2, 0.21, 0.26, 0.3, 0.33, 0.41, 0.54, 0.57, 1.41, 1.7, 1.84, 2.2, 2.26, 3.06, 3.24
Answers
The value of the 10% trimmed mean is approximately 1.3027. To calculate the 10% trimmed mean, we need to trim off the lowest and highest 10% of the data and then find the mean of the remaining values.
First, let's sort the data in ascending order:
0.2, 0.21, 0.26, 0.3, 0.33, 0.41, 0.54, 0.57, 1.41, 1.7, 1.84, 2.2, 2.26, 3.06, 3.24
Next, we calculate the number of values to trim from each end:
10% of 15 (total number of values) = 0.1 * 15 = 1.5
Since we can't remove half a value, we round up to the nearest whole number, which is 2.
Now, we remove the two lowest and two highest values:
0.26, 0.3, 0.33, 0.41, 0.54, 0.57, 1.41, 1.7, 1.84, 2.2, 2.26
Finally, we calculate the mean of the remaining values:
(0.26 + 0.3 + 0.33 + 0.41 + 0.54 + 0.57 + 1.41 + 1.7 + 1.84 + 2.2 + 2.26) / 11 = 14.33 / 11 ≈ 1.3027
Rounding to four decimal places, the value of the 10% trimmed mean is approximately 1.3027.
To know more about statistics refer here;
https://brainly.com/question/32201536?#
#SPJ11
age frequency 21-30 1 31-40 8 41-50 27 51-60 29 61-70 24 71-up 11 total 100 If a CEO is selected at random, find the probability that his or her age is among the following. Part 1 of 4 (a) Over 20 and under 41 P( over 20 and under 41)= Part 2 of 4 (b) Between 31 and 40 P( between 31 and 40)= Part 3 of 4 (c) Under 41 or over 50 P( under 41 or over 50)= Part 4 of 4 (d) Under 41 P( under 41)=
Answers
To answer this question, we need to use the age frequency table given.
Part 1 of 4 (a) Over 20 and under 41:
To find the probability of selecting a CEO whose age is over 20 and under 41, we need to add the frequency of ages 21-30 and 31-40.
P(over 20 and under 41) = frequency of ages 21-30 + frequency of ages 31-40
= 1 + 8
= 9
Therefore, the probability of selecting a CEO whose age is over 20 and under 41 is 9/100 or 0.09.
Part 2 of 4 (b) Between 31 and 40:
To find the probability of selecting a CEO whose age is between 31 and 40, we just need to use the frequency of ages 31-40.
P(between 31 and 40) = frequency of ages 31-40
= 8
Therefore, the probability of selecting a CEO whose age is between 31 and 40 is 8/100 or 0.08.
Part 3 of 4 (c) Under 41 or over 50:
To find the probability of selecting a CEO whose age is under 41 or over 50, we need to add the frequency of ages 21-30, 31-40, and 51-60, 61-70, 71-up.
P(under 41 or over 50) = frequency of ages 21-30 + frequency of ages 31-40 + frequency of ages 51-60 + frequency of ages 61-70 + frequency of ages 71-up
= 1 + 8 + 29 + 24 + 11
= 73
Therefore, the probability of selecting a CEO whose age is under 41 or over 50 is 73/100 or 0.73.
Part 4 of 4 (d) Under 41:
To find the probability of selecting a CEO whose age is under 41, we need to add the frequency of ages 21-30 and 31-40. This is the same as part (a).
P(under 41) = frequency of ages 21-30 + frequency of ages 31-40
= 1 + 8
= 9
Therefore, the probability of selecting a CEO whose age is under 41 is 9/100 or 0.09.
Part 1 of 4 (a) Over 20 and under 41
P(over 20 and under 41) = P(21-30) + P(31-40) = (1 + 8) / 100 = 9/100 = 0.09
Part 2 of 4 (b) Between 31 and 40
P(between 31 and 40) = P(31-40) = 8/100 = 0.08
Part 3 of 4 (c) Under 41 or over 50
P(under 41 or over 50) = P(under 41) + P(over 50) = (P(21-30) + P(31-40)) + (P(51-60) + P(61-70) + P(71-up)) = (1+8+29+24+11)/100 = 73/100 = 0.73
Part 4 of 4 (d) Under 41
P(under 41) = P(21-30) + P(31-40) = (1 + 8) / 100 = 9/100 = 0.09
Learn more about probability here: brainly.com/question/30034780
#SPJ11
lydia graphed δstu at the coordinates s (-3,0), t (0, −3), and u (3, −3). she thinks δstu is a right triangle. is lydia's assertion correct?
Answers
No, Lydia's assertion that δSTU is a right triangle is not correct.
A right triangle is a triangle in which one of the angles measures 90 degrees (a right angle). To determine if δSTU is a right triangle, we need to examine the angles formed by the given coordinates.
Using the coordinates:
s (-3, 0)
t (0, -3)
u (3, -3)
We can calculate the slopes of the lines formed by connecting these points to see if any of them are perpendicular (indicating a right angle).
The slope of the line connecting points s and t is:
m(st) = (y₂ - y₁) / (x₂ - x₁) = (-3 - 0) / (0 - (-3)) = -3/3 = -1
The slope of the line connecting points s and u is:
m(su) = (y₂ - y₁) / (x₂ - x₁) = (-3 - 0) / (3 - (-3)) = -3/6 = -1/2
The slope of the line connecting points t and u is:
m(tu) = (y₂ - y₁) / (x₂ - x₁) = (-3 - (-3)) / (3 - 0) = 0/3 = 0
None of the slopes calculated are perpendicular to each other, meaning none of the angles formed by the given coordinates are 90 degrees. Therefore, δSTU is not a right triangle.
In summary, Lydia's assertion that δSTU is a right triangle is incorrect because the angles formed by the given coordinates do not include a 90-degree angle.
Learn more about triangle here : brainly.com/question/29083884
#SPJ11
Help please i will dm you my sidechick named tyrone

Answers
Answer:
5
Step-by-step explanation:
w = c + ___
means that you add a number to the value of c to get the value of w.
Look at the first line: c = 5; w = 10
What do you add to 5 to get 10?
Answer: 5
5 also works for all the other lines.
6 + 5 = 11
7 + 5 = 12
8 + 5 = 13
The number added to c to get w is always 5.
w = c + 5
Answer: 5
Here are the city gas mileages for 13
different midsized cars in 2008.
16, 15, 22, 21, 24, 19, 20, 20, 21, 27,
18, 21, 48
What is the maximum?
Answers
Answer: 48
Step-by-step explanation: 48 is the highest mileages
Calculate a Confidence Interval for a Population Mean (Standard Deviation Unknown) Question The commute times for the workers in a city are normally distributed with an unknown population mean and standard deviation. If a random sample of 27 workers is taken and results in a sample mean of 22 minutes and sample deviation of 3 minutes, find a 95% confidence interval estimate for the population mean using the Student's t-distribution. df to.10 to.05 to.025 to.01 to.o05 111 25 1.316 1.708 2.060 2.485 2.787 2.779 26 1.315 1.706 2.056 2.479 27 1.314 1.703 2.052 2.473 2.771 28 1.313 1.701 2.048 2.467 2.763 Select the correct answer below: (21.00, 23.00), with ME (1.706) (21.02, 22.98), with ME (1.706) (20.79, 23.21), with ME (2.052) (20.82, 23.18), with ME- (2.052) (21.77, 22.23), with ME (2.056) () (20.81, 23.19), with ME (2.056)
Answers
The 95% confidence interval for population mean is (19.8, 22.2).
The confidence interval for population mean using the Student's t-distribution is:
CI = x ± \(t_{\frac{\alpha }{2}, (n -1) }\) \(\frac{s}{\sqrt{n} }\)
Given:
x = 22
s = 3
n = 27
α = n - 1 = 26
The critical value of t for α = 0.05 and degrees of freedom, (n - 1) = 19 is:
\(t_{\frac{\alpha }{2} , (n -1)}\) = \(t_{\frac{0.05}{2,19} }\)
= 2.093
Compute the 95% confidence interval for population mean as follows:
CI = X + \(t_{\frac{\alpha }{2}, (n -1) }\frac{s}{\sqrt{n} }\)
⇒ CI = 21± 2.093 × 3/√27
= 21 ± 1.20
= (22.2, 19.8)
Thus, the 95% confidence interval for population mean is (19.8, 22.2).
Learn more about Population Mean:
https://brainly.com/question/19538277
#SPJ4
Find The Slope of Each Line

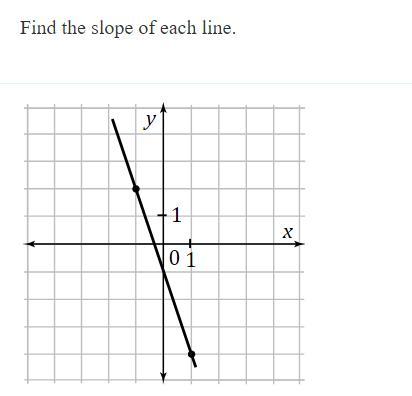

Answers
Answer: 2/8 first answer, 6/2 second answer, 3/2 last answer
Step-by-step explanation: The slope should be the rise over the run, so the answer to the first question would be 2/8 which is rise/run which equals the slope the second answer would be 6/2=slope and the the answer to the last question is 3/2 you start from one point, rise until you get next to the other point on the graph, then you run until you get on that point, the you count your rise which will be the top number of your fraction and then you count your run which will be the bottom number of your fraction. I hope this helped if you could even make sense of all of this.
— 8х + 3y = 17
8x — 9y = — 19
Answers
Answer:
x= 83y−17 and y= 83x+17
hope it helps
math question 1 :) thanks if you help

Answers
Shajdidjsjsjdndndjdudjdjd
Answer:
-9
Step-by-step explanation:
Plug 5 into the equation in place of the x:
- x - 4 becomes -(5) - 4.
-5 - 4 = -9
:)
Kudos if you can answer this.
|2x-7|=7-2x
Find the inequality/solution for x
If bots like link senders answer the question and you cant answer, please answer in the comments. Because i cant give you brainliest like this, i will go to the last 5 questions you have answered and give them all a thanks and a 5 stars.
Your help is appreciated.
Answers
Answer:
X < 7/2
Step-by-step explanation:
Move the variable to the left, separate into possible cases , solve, find the intersections, find the union, and then you get your solution.
Step-by-step explanation:
Given that:
|2x-7| = 7-2x
⇛2x-7 = 7-2x or -(7-2x)
since |x| = a ⇛ x = a or x = -a
⇛2x-7 = 7-2x or 2x-7 = 2x-7
Shift all variables on LHS and constant on RHS, changing it's sign.
⇛2x+2x = 7+7
Add the values on LHS and RHS.
⇛4x = 14
Shift the number 4 from LHS to RHS.
⇛x = 14/4
Write the fraction in lowest form by cancelling method.
⇛ x = {(14÷2)/(4÷2)}
⇛x = 7/2
There is no solution for negative value
x = 7/2
Please let me know if you have any other questions.
Calculate the BMI of an 118-lb adult who is 5 feet 4 inches tall.
Answer:
Logic - BMI formula
703*(lbs/inches^2)
703(118/64^2)=703(118/4096)
703*0.0288=20.2464
Answers
The BMI of an 118-lb adult who is 5 feet 4 inches tall is approximately 20.25.
BMI stands for Body Mass Index.
It's a measure of body fat based on height and weight that applies to both adult men and women.
BMI is an easy-to-perform screening tool for body fat levels that can help identify individuals who have health risks linked with excess body fatness.
It's important to keep in mind that the BMI measurement should not be used as a diagnostic tool for health conditions and is only one component in an overall evaluation of a person's health status.
Using the formula below, we can calculate the BMI of an 118-lb adult who is 5 feet 4 inches tall: BMI = (weight in pounds / (height in inches x height in inches)) x 703
First, we need to convert the height into inches:5 feet 4 inches = 64 inches
Next, we plug the values into the formula and solve for the BMI:
BMI = (118 / (64 x 64)) x 703BMI = (118 / 4,096) x 703BMI = 0.0288 x 703BMI = 20.2464
Therefore, the BMI of an 118-lb adult who is 5 feet 4 inches tall is approximately 20.25.
For more questions on Body Mass Index
https://brainly.com/question/15468401
#SPJ8
The dot plot shows the number of text messages sent by 10 students in one day.
Determine the range of the set:
(1 ) (3) (3) (1) (0) (2)
10. 11. 12. 13. 14. 15.
The number of text messages sent:
Answers
The range of the dataset obtained from the difference between the maximum and minimum value is 5.
Range of a distributionThe range of a distribution or dataset is obtained by subtracting the maximum and minimum values in the distribution.
Range = Maximum - Minimum
From the dataset :
Maximum number of messages sent = 15
Minimum number of messages sent = 10
Range = 15 - 10 = 5
The value of the range in the dataset is 5
Learn more on range ;https://brainly.com/question/10753609
#SPJ1
The range of the set {10, 11, 11, 11, 13, 15, 15} is R = 5.
How to determine the range of a set?For a set of numbers {x₁, x₂, ..., xₙ}
The range is defined as the difference between the largest value and the smallest value.
In this case, we have the set:
{10, 11, 11, 11, 13, 15, 15}
The largest value is 15, and the smallest value is 10, then the range of this set will be:
Range = 15 - 10
Range = 5
The range of the set is 5 units.
Learn more about range at:
https://brainly.com/question/10197594
#SPJ1
Which recursive formula can be used to determine the total amount of time spent making hats based on the total amount of time spent previously?
f(n + 1) = f(n) + 1.5
f(n + 1) = f(n) + 0.75
f(n + 1) = one-halff(n)
f(n + 1) = three-halvesf(n)
Answers
Answer:
B
Step-by-step explanation:

Answer:
b
Step-by-step explanation:
because i just know
When a fixed bridge is created, there must be at least_______of the bridge
Answers
Answer: One abutment
Step-by-step explanation: When a fixed bridge is created, there must be at least one abutment of the bridge.
the right hand side value for the starting node in a shortest path problem has a value of
Answers
In a shortest path problem, the right-hand side (RHS) value for the starting node has a value of 0. This indicates that the shortest path from the starting node to itself has a cost of 0.
In summary, the RHS value for the starting node in a shortest path problem is 0, indicating that the shortest path from the starting node to itself has a cost of 0.
The RHS value is used in the context of the Dijkstra's algorithm, which is commonly used to solve shortest path problems. In this algorithm, a priority queue is used to store the nodes that have not yet been visited, sorted based on their tentative distances from the starting node. Initially, the starting node is assigned a tentative distance of 0, indicating that it is the source node for the shortest path. The RHS value is used to update the tentative distance of a node when a shorter path is discovered. When a node is added to the priority queue, its tentative distance is compared to its RHS value, and the smaller of the two values is used as the node's priority in the queue. By setting the RHS value of the starting node to 0, we ensure that the starting node always has the highest priority in the queue and is processed first by the algorithm.
To learn more about Dijkstra's algorithm click here, brainly.com/question/30767850
#SPJ11
Solve the differential equation y" +4y' +4y=e²* cos 3x using the method of undetermined coefficients.
Answers
The particular solution is: \(y_p\)(x) = e^(-x) * cos(3x). To solve the given differential equation using the method of undetermined coefficients, we assume a particular solution of the form:
y_p(x) = Ae^(λx) * cos(3x) + Be^(λx) * sin(3x)
where A and B are undetermined coefficients, and λ is the constant we need to determine.
We start by finding the derivatives of y_p(x):
y_p'(x) = Aλe^(λx) * cos(3x) - 3Ae^(λx) * sin(3x) + Bλe^(λx) * sin(3x) + 3Be^(λx) * cos(3x)
y_p''(x) = Aλ^2e^(λx) * cos(3x) - 6Aλe^(λx) * sin(3x) - 3Ae^(λx) * sin(3x) - 3Bλe^(λx) * sin(3x) + Bλ^2e^(λx) * sin(3x) + 3Be^(λx) * cos(3x)
Now, we substitute y_p(x), y_p'(x), and y_p''(x) into the original differential equation:
[Aλ^2e^(λx) * cos(3x) - 6Aλe^(λx) * sin(3x) - 3Ae^(λx) * sin(3x) - 3Bλe^(λx) * sin(3x) + Bλ^2e^(λx) * sin(3x) + 3Be^(λx) * cos(3x)]
4[Aλe^(λx) * cos(3x) - 3Ae^(λx) * sin(3x) + Bλe^(λx) * sin(3x) + 3Be^(λx) * cos(3x)]
4[Ae^(λx) * cos(3x) + Be^(λx) * sin(3x)]
= e^(2x) * cos(3x)
Now, we can simplify the equation:
[Aλ^2 + 4Aλ + 4A] * e^(λx) * cos(3x) + [Bλ^2 + 4Bλ + 4B] * e^(λx) * sin(3x)
= e^(2x) * cos(3x)
For the equation to hold true for all values of x, the coefficients of each term must be equal:
Aλ^2 + 4Aλ + 4A = 1
Bλ^2 + 4Bλ + 4B = 0
Solving the first equation, we have:
λ^2 + 4λ + 4 = 1
λ^2 + 4λ + 3 = 0
This is a quadratic equation that can be factored:
(λ + 1)(λ + 3) = 0
λ = -1 or λ = -3
Now, let's solve the second equation for λ = -1 and λ = -3:
For λ = -1:
B*(-1)^2 + 4B*(-1) + 4B = 0
B - 4B + 4B = 0
B = 0
For λ = -3:
B*(-3)^2 + 4B*(-3) + 4B = 0
9B - 12B + 4B = 0
B = 0
Therefore, for both values of λ, B = 0.
Now, we can find the value of A:
Aλ^2 + 4Aλ + 4A = 1
For λ = -1:
A*(-1)^2 + 4A*(-1) + 4A = 1
A - 4A + 4A = 1
A = 1
For λ = -3:
A*(-3)^2 + 4A*(-3) + 4A = 1
9A - 12A + 4A = 1
A = 1/5
Therefore, for λ = -1, A = 1, and for λ = -3, A = 1/5.
The particular solution is:
\(y_p\)(x) = e^(-x) * cos(3x)
To learn more about undetermined coefficients visit:
brainly.com/question/30584001
#SPJ11
jane is 3 times as old as kate. in 5 years jane's age will be 2 less than twice kate's. how old are the girls now
Answers
Answer:
Kate is 3 years old, Jane is 9 years old
Step-by-step explanation:
1.) First, assign variables to all of their ages. If we say Kate's age is x, Jane's age is 3 times this, which can be written as j, is 3x.
2.) Jane's age is also 2 less than twice of Kate's in 5 years. This means that her age is also 2(x+5) - 2 = j + 5. With a little simplification, you get that 2x + 8 = j + 5.
3.) Since j, Jane's age, is also 3x, we can substitute 3x in for j in the second equation. If you do this, you get 2x + 8 = 3x + 5.
4.) By moving the x onto one side and the numbers onto another, you get x = 3. X was Kate's age, meaning that Kate is 3 years old.
5.) Finally, since Jane's age is 3 times Kate's age, Jane's age is 3 * 3, which is 9. Jane is 9 years old.
Jane is 9 years old and Kate is 3 years old.To solve the problem, let's first establish variables for Jane and Kate's ages.
Let J represent Jane's age and K represent Kate's age.
According to the student question, Jane is 3 times as old as Kate, which can be represented as:
J = 3K
In 5 years, Jane's age will be 2 less than twice Kate's age, which can be represented as:
J + 5 = 2(K + 5) - 2
Now we can solve the equations step by step:
Substitute the first equation into the second equation to eliminate one of the variables:
3K + 5 = 2(K + 5) - 2
Distribute the 2 on the right side of the equation:
3K + 5 = 2K + 10 - 2
Simplify the equation by combining like terms:
3K + 5 = 2K + 8
Move the 2K term to the left side of the equation:
K = 3
now we know that Kate is currently 3 years old.
Substitute K's value back into the first equation to find Jane's age:
J = 3K
J = 3(3)
Simplify to find Jane's age:
J = 9
So, Jane is currently 9 years old.
Jane is 9 years old and Kate is 3 years old.
for more questions on variables
https://brainly.com/question/9302141
#SPJ11
ABC = EDC, AB = 7, A = 40° E=

Answers
Answer:
40°Step-by-step explanation:
since ΔABC is ≅ to ΔEDC
where ∠A = 40°
∠E = 40° because ∠A ≅ ∠E

The equation for the axis of symmetry is
Answers
Answer:
I believe it is x=−b2a
Step-by-step explanation:
Looked it up
A circle's radius is 16 centimeters.
What is the circle's circumference (use 3.14 for pi and round to the
nearest tenth)?
Answers
Answer:
100.5 cm
Step-by-step explanation:
The circumference of a circle is given by the formula ...
C = 2πr
Using the given values, we find ...
C = 2(3.14)(16 cm) ≈ 100.5 cm . . . circumference of the circle
Mr. Martin is giving a math test next period. The test, which is worth 100 points, has 29 problems. Each problem is worth either 5 points or 2 points. Write a system of equations that can be used to find how many problems of each point value are on the test.
PLEASE HELP
SERIOUS ANSWERS ONLY
I WILL REPORT YOU AND DO A FORMAL COMPLAINT
Let x be the number of questions worth 5 points and let y be the number of questions worth 2 points.
x + y = 29, 5x + 2y = 100
x + y = 100, 5x + 2y = 29
5x + y = 29, 2y + x = 100
2x + y = 100, 5y + x = 29
Answers
Answer:
it A
x + y = 29, 5x + 2y = 100
Step-by-step explanation:
Answer:
A, x + y = 29, 5x + 2y = 100
Step-by-step explanation:
just finished the assignment on edg 2020
200 = 1000 - n/4. What is the value of n? Show working out, please.
Answers
Answer:
n = 3200
Step-by-step explanation:
200 = 1000 - \(\frac{n}{4}\) ( subtract 1000 from both sides )
- 800 = - \(\frac{n}{4}\) ( multiply both sides by 4 to clear the fraction )
- 3200 = - n ( multiply both sides by - 1 )
n = 3200
The velocity as a function of time for an asteroid in the asteroid belt is given by v(t)=v0e−t/t^+2tvt^ where v0 and t0 are constants. these questions do not have to be answered in the order in which they are asked (it may be easier to answer them in a different order). The values for the constants that you will use are: v0=2 m/st0=336 s Displacement Average x Component of the Velocity Magnitude of Average Acceleration Final Speed Find the speed of the asteroid at the final time. v(ff)=
Answers
The speed of the asteroid at the final time is infinity.
Given, the velocity as a function of time for an asteroid in the asteroid belt is given by: v(t) = v0 * e^(-t/t0) + 2t * v0
Here, v0 and t0 are constants.
Now, let's find the velocity at final time by substituting the given values:
v(t) = v0 * e^(-t/t0) + 2t * v0v(t) = 2 * e^(-t/336) + 2t * 2m/s
t(t0 = 336 seconds and v0 = 2 m/s)
Now, let's find the velocity at the final time i.e v(ff)
v(ff) = v(∞) = 2 * e^(-∞/336) + 2 * ∞ * 2 m/s = 0 + ∞ = ∞
Thus, the speed of the asteroid at the final time is infinity.
To know more about speed, visit:
https://brainly.com/question/17661499
#SPJ11
(c) prove that for any positive integer n, 4 evenly divides 11n - 7n.
Answers
By mathematical induction, we have proved that for any positive integer n, 4 evenly divides 11n - 7n.
WHat is Divisibility?
Divisibility is a mathematical property that describes whether one number can be divided evenly by another number without leaving a remainder. If a number is divisible by another number, it means that the division process results in a whole number without any remainder. For example, 15 is divisible by 3
To prove that 4 evenly divides 11n - 7n for any positive integer n, we can use mathematical induction.
Base Case:
When n = 1, 11n - 7n = 11(1) - 7(1) = 4, which is divisible by 4.
Inductive Step:
Assume that 4 evenly divides 11n - 7n for some positive integer k, i.e., 11k - 7k is divisible by 4.
We need to prove that 4 evenly divides 11(k+1) - 7(k+1), which is (11k + 11) - (7k + 7) = (11k - 7k) + (11 - 7) = 4k + 4.
Since 4 evenly divides 4k, and 4 evenly divides 4, it follows that 4 evenly divides 4k + 4.
By mathematical induction, we have proved that for any positive integer n, 4 evenly divides 11n - 7n.
To know more about Divisibility visit:
https://brainly.com/question/9462805
#SPJ4
help please what are the features of the function f(x) = -(1/3)^x +5 graphed below (it's all in the picture)
Answers
The requried features of the given function has been shown below.
The function f(x) = -(1/3)^x +5 has the following features:
Domain: The domain of the function is all real numbers.
Range: The range of the function is y ≤ 5. In other words, the function has a maximum value of 5, which is approached but never reached as x approaches negative infinity.
x-intercept: The x-intercept is where the graph of the function intersects the x-axis. The x-intercept is approximately -3.96.
y-intercept: The y-intercept is where the graph of the function intersects the y-axis. The y-intercept is (0, 4).
Learn more about function here:
https://brainly.com/question/12431044
#SPJ1
