PLZ ANSWER THESE THREE QUESTIONS I WILL MARK AS BRAINLIEST
Write (7x⁵)² as a single power of x
Write (4x⁷)³ as a single power of x
Write (2x⁶)⁶ as a single power of x
Answers
Step-by-step explanation:
(7x^5)^2 = 49x^10
(4x^7)^3 = 64x^21
(2x^6)^6 = 64x^36
Related Questions
Write the equations of two cubic functions whose only x-intercepts are (-2, 0) and (5, 0) and whose y-intercept is (0, 20).
Answers
Two cubic functions with x-intercepts at (-2, 0) and (5, 0), and a y-intercept at (0, 20) can be represented by the equations f(x) = k(x + 2)(x - 5)(x - r) and g(x) = k(x + 2)(x - 5)(x + r), where r is a constant.
To find the equations of the cubic functions, we can start by considering the x-intercepts. Given that the x-intercepts are (-2, 0) and (5, 0), we know that the factors in the equations will be (x + 2) and (x - 5), respectively. To include the y-intercept at (0, 20), we need to determine the constant k.
For the first cubic function, let's denote it as f(x), we introduce another factor (x - r) to the equation. The complete equation becomes f(x) = k(x + 2)(x - 5)(x - r). Substituting the y-intercept, we have 20 = k(0 + 2)(0 - 5)(0 - r), which simplifies to 20 = -10kr. Solving for k, we find k = -2/r.
For the second cubic function, denoted as g(x), we introduce (x + r) as the additional factor. The equation becomes g(x) = k(x + 2)(x - 5)(x + r). Substituting the y-intercept, we have 20 = k(0 + 2)(0 - 5)(0 + r), which simplifies to 20 = 10kr. Solving for k, we find k = 2/r.
Therefore, the equations of the two cubic functions with the given x-intercepts and y-intercept are f(x) = -2(x + 2)(x - 5)(x - r) and g(x) = 2(x + 2)(x - 5)(x + r), where r is a constant.
Learn more about cubic here: https://brainly.com/question/31346659
#SPJ11
4. There are major chords built on what three notes (with all white notes and no accidentals)? O CFG O ABC GEB OCDE
Answers
The three major chords built on white notes without accidentals are:
1. C major chord (C, E, G)
2. F major chord (F, A, C)
3. G major chord (G, B, D)
These chords are formed by taking the root note, skipping one white note, and adding the next white note on top. For example, in the C major chord, the notes C, E, and G are played together to create a harmonious sound.
Similarly, the F major chord is formed by playing F, A, and C, and the G major chord is formed by playing G, B, and D. These three major chords are commonly used in various musical compositions and are fundamental building blocks in music theory.
To know more about musical chords, visit,
https://brainly.com/question/14936810
#SPJ4
Which is equal to K-L ?

Answers
Answer:7 -3
6 0
13-6=7
7-10=-3
25-19=6
18-18=0
Step-by-step explanation:
Answer:
third option from the top
Step-by-step explanation:
7. -3
6. 0
Please help help help help help please ASAP

Answers
Answer
~~~~~~~~~~~~
slope: 1
y intercept: 4
equation: y=x+4
help meeee plezzzzzzz

Answers
Use PEMDAS to show your answer
Answer:
-16
Step-by-step explanation:
Or you could use desmos scientific calculator
pleasee helpppp!!!!
A man is 47 years old, and his sister is 43 years old. How many years ago was the man twice as old as his sister?
Answers
Answer:39 years ago
Step-by-step explanation:The difference between his age and his sister's is 4.So when he was 8 she 4.So you do 47-8 which is 39.
A store sells grape jelly in 15-ounce jars for $13.59. Find the price per ounce
Answers
Answer:
91 cents per ounce
Step-by-step explanation:
Divide 13.59 by 15
Answer: $0.91
Step-by-step explanation:
Take $13.59 divided by 15 = $0.91 per ounce
If you can, please give me a Brainliest, I need 2 more to get to the highest rank, thank you!
Solve for x in this problem √x-2 +4=x
Answers
The Radical Form (√x) ,the solutions to the equation √x - 2 + 4 = x are x = 1 and x = 4.
The equation √x - 2 + 4 = x for x, we can follow these steps:
1. Begin by isolating the radical term (√x) on one side of the equation. Move the constant term (-2) and the linear term (+4) to the other side of the equation:
√x = x - 4 + 2
2. Simplify the expression on the right side of the equation:
√x = x - 2
3. Square both sides of the equation to eliminate the square root:
(√x)^2 = (x - 2)^2
4. Simplify the equation further:
x = (x - 2)^2
5. Expand the right side of the equation using the square of a binomial:
x = (x - 2)(x - 2)
x = x^2 - 2x - 2x + 4
x = x^2 - 4x + 4
6. Move all terms to one side of the equation to set it equal to zero:
x^2 - 4x + 4 - x = 0
x^2 - 5x + 4 = 0
7. Factor the quadratic equation:
(x - 1)(x - 4) = 0
8. Apply the zero product property and set each factor equal to zero:
x - 1 = 0 or x - 4 = 0
9. Solve for x in each equation:
x = 1 or x = 4
Therefore, the solutions to the equation √x - 2 + 4 = x are x = 1 and x = 4.
To know more about Radical form .
https://brainly.com/question/29153583
#SPJ8
Consider the following Linear Programming Problem (LPP):
Maximize Z = 3x1 + 2x2 Subject to
x1 ≤ 4
x2 ≤ 6
3x1 + 2x2 ≤ 18
x1 ≥ 0, x2 ≥ 0
Answers
The given linear programming problem aims to maximize the objective function \(Z = 3x1 + 2x2\), subject to four constraints: x1 ≤ 4, x2 ≤ 6, 3x1 + 2x2 ≤ 18, and x1 ≥ 0, x2 ≥ 0.
The objective of linear programming is to optimize (maximize or minimize) a linear objective function while satisfying a set of linear constraints. In this case, the objective is to maximize \(Z = 3x1 + 2x2\).
The constraints in the problem define the feasible region, which is the set of all points that satisfy the constraints. The constraints state that x1 must be less than or equal to 4, x2 must be less than or equal to 6, and the linear combination \(3x1 + 2x2\) must be less than or equal to 18. Additionally, both x1 and x2 must be greater than or equal to zero.
To solve this linear programming problem, graphical methods or optimization algorithms such as the simplex method can be employed. The feasible region is determined by graphing the constraints and finding the overlapping region. The optimal solution is the point within the feasible region that maximizes the objective function.
The explanation of the solution, including the optimal values of x1 and x2, the maximum value of Z, and the graphical representation of the problem, can be provided based on the chosen method of solving the linear programming problem.
Learn more about Linear Programming problem (LPP) here:
https://brainly.com/question/29405467
#SPJ11
One half of the number of roses julia planted in her garden is 2/5 the number of tulips she planted, what was the ratio of the number of tulips to roses in the garden
Answers
The ratio of the number of tulips to roses in Julia's garden is 5:4.
A ratio is a quantitative comparison between two or more quantities or values.
Let the number of roses Julia planted is denoted by 'R',
and the number of tulips she planted is denoted by 'T'.
According to the given information,
"One half of the number of roses Julia planted is 2/5 the number of tulips she planted."
So, the mathematical expression is
(1/2)R = (2/5)T
T = (5/2)(1/2)R
T = (5/4)R
As, the ratio of the number of tulips to roses is T:R, which can be expressed as (5/4):1 or simply 5:4.
Therefore, the ratio is 5:4.
Learn more about Ratio here:
https://brainly.com/question/26215397
#SPJ12
The ratio of the angles in a triangle is 2:3:4. What is the measure of the largest angle?
30°
60°
80°
20°
Answers
Answer:
80
Step-by-step explanation:
you can take the ratio 2:3:4 as
2x + 3x + 4x = 180
9x = 180
x= 20
4(20) = 80
Answer:
D) 20
Step-by-step explanation:
Set up an equation: 2x+3x+4x=180
9x=180
180/9=20
Answer: D) 20degrees
Select all equations that have graphs with the same y-intercept.
Answers
Answer:
there ar no graphs. Wish i could help. To add a screenshot, select the paperclip icon when posting a question and add the image like that.
If you need to know how to take a screenshot on your device, tell me the brand and name of your device
Example: Brand; Acer, Name; Chromebook
Step-by-step explanation:
Ten cards are randomly chosen from a deck of 52 cards. Each of the selected cards is put in one of 4 piles, depending on the suit of the card. What is the probability that the largest pile has 4 cards, the next largest has 3, the next largest has 2, and the smallest has 1?
Answers
The probability that the largest pile has 4 cards, the next largest has 3, the next largest has 2, and the smallest has 1 is approximately 0.012 or 1.2%.
To solve this problem, we need to count the number of ways to choose 10 cards from a deck of 52 cards and then divide by the total number of ways to put these cards into 4 piles.
Step 1: Count the total number of ways to choose 10 cards from a deck of 52 cards using the combination formula:
C(52, 10) = 52! / (10! × 42!) = 158,200,242,880 / (3,628,800 × 99,884,160) = 1,787,671
Step 2: Count the total number of ways to put 10 cards into 4 piles. We can think of each card as having 4 choices, one for each pile. Therefore, the total number of ways to put the cards into piles is:
\(4^{10}\) = 1,048,576
Step 3: Count the number of ways to put 10 cards into 4 piles such that the largest pile has 4 cards, the next largest has 3, the next largest has 2, and the smallest has 1.
First, we need to choose 4 cards from the 10 cards to go into the largest pile. This can be done in C(10,4) ways:
C(10,4) = 10! / (4! × 6!) = 210
Then, we need to choose 3 cards from the remaining 6 cards to go into the next largest pile. This can be done in C(6,3) ways:
C(6,3) = 6! / (3! × 3!) = 20
Next, we need to choose 2 cards from the remaining 3 cards to go into the next largest pile. This can be done in C(3,2) ways:
C(3,2) = 3! / (2! × 1!) = 3
Finally, the remaining card goes into the smallest pile. Therefore, there is only one way to put the card into the smallest pile.
Therefore, the total number of ways to put 10 cards into 4 piles such that the largest pile has 4 cards, the next largest has 3, the next largest has 2, and the smallest has 1 is:
C(10,4) × C(6,3) × C(3,2) × 1 = 210 × 20 × 3 × 1 = 12,600
Step 4: Calculate the likelihood by dividing the number of ways in Step 3 by the number of ways in Step 2:
P = 12,600 / 1,048,576 = 0.012 or 1.2%.
Learn more about the probability at
brainly.com/question/12619550
#SPJ4
Helllllpppp meeeee I neeedddd hellllpppp nowwww pleaseeee

Answers
Answer:
C
Step-by-step explanation:
They are all integers so they are rational numbers, they are whole numbers as well except there are negative numbers so they are not all natural.
1-You are werdding photograher. You are preparing to photograph wedding party consisting of 5 bridemaids. 5 groomsmen, the bride, and the groom. How many people should be in this photo ?
Answers
EXPLANATION
In this photo should be 5+5+1+1=12 people.
The answer is 12 people.
Find the volume of the sphere

Answers
Answer: If you use 3.14 for pi you get 2858.09
But if you use the actual pi symbol you get 2144.6
Step-by-step explanation:
The formula for a sphere is v=4/3r³
Using 3.14: V= 4/3·3.14·8³
V= 4/3·3.14·512
V=2858.09
And using the actual pi symbol using the same steps gets you 2144.6
heres a pic of my dog :) her name is tess

Answers
Answer:
She is so adorable
Step-by-step explanation:
Very adorable doggo
Answer:
She's adorable!! What type of dog is she?
Step-by-step explanation:
I have two rottweilers and I love them sooooo much <3
Which statements are true? Select all that apply.
81 is a perfect square.
75 is a perfect cube.
729 is a perfect cube.
32 is neither a perfect square nor a perfect cube.
81 is both a perfect square and a perfect cube.
Answers
The following statements are true:
81 is a perfect square.
729 is a perfect cube.
We have,
- 81 is a perfect square because it can be expressed as the square of a whole number.
In this case, 81 is equal to 9², where 9 is the square root of 81.
- 729 is a perfect cube because it can be expressed as the cube of a whole number.
In this case, 729 is equal to 9³, where 9 is the cube root of 729.
The statement "81 is both a perfect square and a perfect cube" is incorrect. While 81 is a perfect square, it is not a perfect cube because it cannot be expressed as the cube of a whole number.
Thus,
The following statements are true:
81 is a perfect square.
729 is a perfect cube.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ6
what is 1,000,000,000 divided by -1,000
Answers
-1000000 that is the answer
hope this helps!
How to do this problem?? Thank u

Answers
Answer:
meron po bang pagpipilian ng sagot
Explain the 'price effect' for normal 'substitutes' and 'complementary' goods.
Answers
Answer:
When the price of a good that complements a good decrease, then the quantity demanded of one increases and the demand for the other increases. When the price of a substitute good decreases, the quantity demanded that good increases, but the demand for the good that it is being substituted for decreases.
Please help Expert and Above Only! I will double the points if you can explain it! Both questions please!

Answers
Problem 11
Answer: 339 square meters---------------
Work Shown:
The surface area of a 3D sphere is 4pi*r^2. So a hemisphere has surface area 2pi*r^2 since we cut the surface area in half.
Plug in r = 6 (half of the diameter 12) and we get 2pi*r^2 = 2pi*6^2 = 72pi
Now consider the circle with radius r = 6. Its area is pi*r^2 = pi*6^2 = 36pi
Add the two areas and we get 72pi+36pi = 108pi
Lastly, use your calculator to get 108pi = 108*3.1415926535898 = 339.292006587699 which rounds to 339
======================================
Problem 12
Answer: C) 19.5 mm---------------
Explanation:
Look at where the "0" in the bottom sliding portion lines up with the number scale above. That "0" is between 19 and 20 mm. So you could argue that 19.2 and 19.5 are both valid answers, but I think 19.5 is the better answer since the tickmark seems to be right in the middle (more or less).
Step-by-step explanation:
surface area of hemisphere =3πr²
=3*3.14(6)²
=339.12m²
diameter of pipe= 19.5mm
let be the tangent plane to the graph of (,)=26−132−262 at the point (4,2,−286). let (,)=26−2−2. find the point on the graph of where the tangent plane is parallel to .
Answers
The point on the graph where the tangent plane is parallel is (52, 52, -5382).
What is the tangent plane?
The surface that contains all tangent lines of the curve at a point, $P$, that lies on the surface and passes through the point is represented by the tangent plane. We discovered earlier in our talks of derivatives and tangent lines that we can use tangent lines to mimic the behavior of a graph. We may employ tangent planes for a similar reason now that we're working with multivariable functions and three-dimensional coordinate systems.
Here, we have
Given: Let P be the tangent plane to the graph of g(x, y) = 26 – 13x² – 26y² at the point (4, 2, –286). Let f(x, y) = 26 – x² - y².
We have to find the point on the graph where the tangent plane is parallel.
Let P be the tangent plane to the graph z = g(x, y) = 26 – 13x² – 26y² at the point (4, 2, –286).
φ(x,y,z) = 13x² + 26y² + z - 26
Δφ = 26xi + 52yj + k
Δφ(4, 2, –286) = 104i + 104j + k
Then,
P: 104(x-4) + 104(y-2)+1(z+286) = 0
104x + 104y + z = 338...(1)
Now, Let
ψ(x,y,z) = x² + y² + z - 26
Δψ = 2xi + 2yj + k
Let (x₀,y₀,z₀) be the point of the graph z = f(x,y) = 26 – x² - y² where the tangent plane in the plane is parallel to equation (1).
Δψ (x₀,y₀,z₀) = (2x₀,2y₀,1)
= 2x₀/104 = 2y₀/104 = 1/1
x₀ = 52 = y₀
Now, z₀ = 26 – x₀² - y₀² = 26 – 52² - 52²= -5382
Hence, the point on the graph where the tangent plane is parallel is (52, 52, -5382).
To learn more about the tangent plane from the given link
https://brainly.com/question/30452856
#SPJ4
please help, thank u
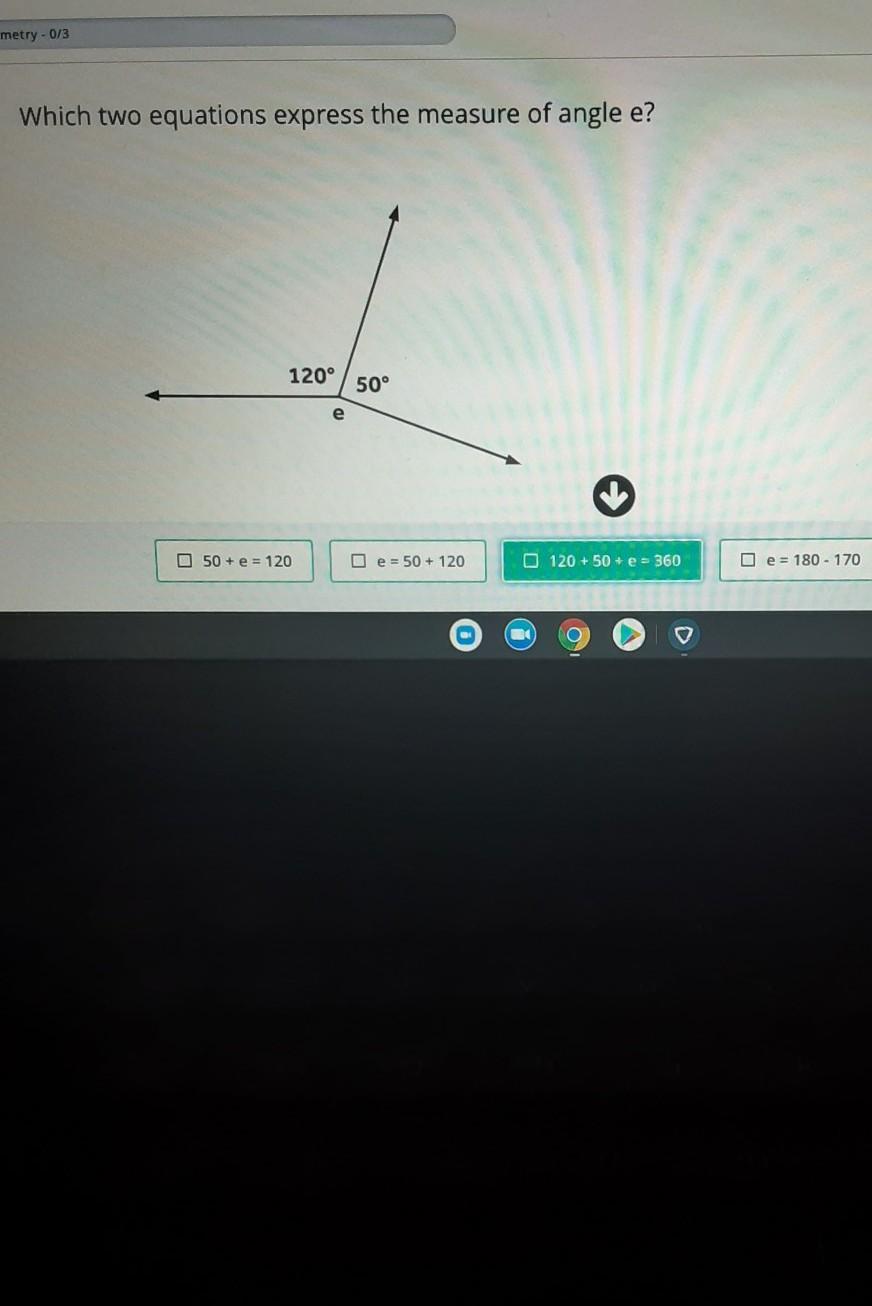
Answers
Answer:
B and C
Step-by-step explanation:
Keisha buys 2 pens at the store. Each pen costs $2. Which graph shows the coordinates of the point that represents the number of pens that Keisha buys and the total cost? PLES IM DOING A TEST RN
Answers
The coordinate of the point that represents the number of pens that Keisha buys and the total cost is (2, 4)
How to determine the graph shows the coordinates of the point that represents the number of pens that Keisha buys and the total cost?The given parameters are
Number of pen = 2
Unit price = $2
This means that the total amount spent is
Total amount = Number of pen * Unit price
Evaluate the product
Total amount = 2 * 2
Evaluate the product
Total amount = 4
So, the coordinate of the point that represents the number of pens that Keisha buys and the total cost is (2, 4)
Read more about coordinate at:
https://brainly.com/question/17206319
#SPJ1
Twice a certain number minus 4 is equal to five. pls help me with it
Answers
2x - 4 = 5
2x - 4 + 4 = 5 + 4
2x = 9
x = 9/2
Step-by-step explanation:
let the number be x
x+x -4=5
2x- 4=5
2x =5+4
2x =9
divide both sides by 2
x=9/2=4.5
Kent multiplies both sides of the equation below by an expression. Then he moves all the terms to one side of the equal sign in the resulting equation. Which equation must he solve now
Answers
The equation must satisfies the Kent calculation is k² - 8k + 12 = 0
The term equation in math is called as a mathematical expression that contains an equals symbol.
Here we have given that Kent multiplies both sides of the equation below by an expression.
And then he moves all the terms to one side of the equal sign in the resulting equation.
Here we have the given equation is
=> k+12/k= 8
When we multiply both sides by k.
=> k² + 12 = 8k
Now we have to subtract 8k from both sides to move all the terms to one side of the equal sign then we get
=> k² + 12 - 8k = 0
Hence the required equation is k2 - 8k + 12 = 0.
To know more about equation here.
https://brainly.com/question/10413253
#SPJ4
the Iine segment from P to Q by a vector-valued function. ( P corresponds to t=0.Q corresponds to t=1. ) P(−8,−4,−4),Q(−1,−9,−6)
Answers
The vector-valued function of the line segment from P to Q is:
r(t) = (-8 + 7t, -4 - 5t, -4 - 2t)
Given that the coordinates of point P are (-8, -4, -4) and the coordinates of point Q are (-1, -9, -6). Let the vector be given by `r(t)`. Since P corresponds to `t=0` and Q corresponds to `t=1`, we can write the vector-valued function of the line segment from P to Q as:
r(t) = (1 - t)P + tQ where 0 ≤ t ≤ 1.
To verify that `r(t)` traces the line segment from P to Q, we can find `r(0)` and `r(1)`.
r(0) = (1 - 0)P + 0Q
= P = (-8, -4, -4)r(1)
= (1 - 1)P + 1Q
= Q = (-1, -9, -6)
Therefore, the vector-valued function of the line segment from P to Q is given by:
r(t) = (-8(1 - t) + (-1)t, -4(1 - t) + (-9)t, -4(1 - t) + (-6)t)
= (-8 + 7t, -4 - 5t, -4 - 2t)
Thus, the vector-valued function of the line segment from P to Q is:
r(t) = (-8 + 7t, -4 - 5t, -4 - 2t)
To know more about vector-valued function visit:
https://brainly.com/question/33066980
#SPJ11
Given that f(x)= 4x-3 and g(x)= 2x-1 over 3 solve for g(f(2))
Answers
Answer:
\(g(f(2))=3\)
Step-by-step explanation:
So we have:
\(f(x)=4x-3\text{ and } g(x)=\frac{2x-1}{3}\)
And we want to solve for g(f(2)).
First, find f(2):
\(f(2)=4(2)-3\)
Multiply:
\(f(2)=8-3\)
Subtract:
\(f(2)=5\)
Now, substitute this in for g(f(2)):
\(g(f(2))=g(5)\)
Substitute this in for g(x):
\(g(5)=\frac{2(5)-1}{3}\)
Multiply:
\(g(5)=\frac{10-1}{3}\)
Subtract:
\(g(5)=\frac{9}{3}\)
Divide:
\(g(5)=3\)
Therefore:
\(g(f(2))=3\)
The line, y = 3x+2, is tangent to the circle with centre, C(-5,4), at the point Q.
Find the coordinates of Q.
Answers
The circle centered at C(-5,4) intersects the line y = 3x + 2 at the point Q, with coordinates (-1/10, 17/10). This point Q serves as the tangent point between the line and the circle.
To find the coordinates of the point Q where the line y = 3x + 2 is tangent to the circle with center C(-5,4), we can use the concept of the slope of a tangent line.
First, we need to find the slope of the tangent line. The slope of the line y = 3x + 2 is 3. For a tangent line to a circle, the radius drawn from the center of the circle to the point of tangency is perpendicular to the tangent line. Since the slope of the radius is the negative reciprocal of the tangent line's slope, the slope of the radius is -1/3.
Next, we find the equation of the radius line passing through the center C(-5,4) with a slope of -1/3. Using the point-slope form, we have:
y - 4 = (-1/3)(x + 5)
To find the point of tangency, we solve the system of equations formed by the line y = 3x + 2 and the radius line:
y = 3x + 2
y - 4 = (-1/3)(x + 5)
Substituting the value of y from the first equation into the second equation:
3x + 2 - 4 = (-1/3)(x + 5)
3x - 2 = (-1/3)x - 5/3
3x + (1/3)x = 5/3 - 2
(10/3)x = -1/3
x = -1/10
Substituting this value of x back into the first equation:
y = 3(-1/10) + 2
y = -3/10 + 20/10
y = 17/10
Therefore, the coordinates of the point Q, where the line y = 3x + 2 is tangent to the circle with center C(-5,4), are (-1/10, 17/10)
For more question on tangent visit:
https://brainly.com/question/30760562
#SPJ8