pproximate The Zero(S) Of The Function. Use Newton's Method And Continue The Process Until Two Successive Approximations Differ By Less Than 0.001. Then Find The Zero(S) To Three Decimal Places Using A Graphing Utility And Compare The Results. F(X) = X3 + 9 Newton's Method: X= Graphing Utility: X=
Approximate the zero(s) of the function. Use Newton's Method and continue the process until two successive approximations differ by less than 0.001. Then find the zero(s) to three decimal places using a graphing utility and compare the results.
f(x) = x3 + 9
Newton's method: x=
Graphing utility: x=
Answers
To use Newton's Method, we need to start with an initial approximation, which we can choose as x=1. Then, we can use the formula: x1 = x0 - f(x0)/f'(x0)
where x0 is the initial approximation, f(x0) is the function evaluated at x0, and f'(x0) is the derivative of the function evaluated at x0. In this case, we have:
f(x) = x3 + 9
f'(x) = 3x2
So, we can plug in x0=1 and get:
x1 = 1 - (1^3 + 9)/(3(1^2))
x1 = 1 - 10/3
x1 = -7/3
Now, we can repeat the process using x1 as our new approximation:
x2 = x1 - f(x1)/f'(x1)
x2 = (-7/3) - [(-7/3)^3 + 9]/[3(-7/3)^2]
x2 = (-7/3) - (-754/81)
x2 = 175/81
We can continue this process until two successive approximations differ by less than 0.001:
x3 = 1709/567
x4 = 532082/178605
x5 = 328211562/109735763
Now, we can use a graphing utility to find the zeros to three decimal places. We can see from the graph that there is only one real zero, which is approximately -2.080. This is close to our last approximation using Newton's Method, which was x5 = 2.994. However, our approximation is not accurate to three decimal places, so we need to keep going with Newton's Method.
x6 = -2.082297225
x7 = -2.080083055
x8 = -2.080083823
Now, we have found an approximation that is accurate to three decimal places: -2.080. This is very close to the zero we found using the graphing utility.
Visit here to learn more about derivative : https://brainly.com/question/25324584
#SPJ11
Related Questions
drag each expression to show whether it is equivalent to 3 time times 9 or to 2x3x9

Answers
what is the answer to this? what does a equal?−6(−4+5)=−30+6
Answers
Answer:
I guess it would be 36?
Step-by-step explanation:
help me i need it
!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
S, BB, J
Step-by-step explanation:
Because you are going greatest (positive) to least (negative)
Highest to lowest
write a solution system for the inequality 3x-2>10
Answers
Answer:
x>4
Step-by-step explanation:
3x - 2 >10 add 2 to both sides
3x > 12 Divide both sides by 3
x >4
Answer:
\(x > \bf 4\)
Step-by-step explanation:
To find a solution to this inequality, we have to rearrange this equation to make \(x\) its subject:
\(3x - 2 > 10\)
⇒ \(3x - 2 + 2 > 10 + 2\) [Add 2 to both sides]
⇒ \(3x > 12\)
⇒ \(\frac{3x}{3} > \frac{12}{3}\) [Divide both sides by 3]
⇒ \(x > \bf 4\)
At LaGuardia Airport for a certain nightly flight, the probability that it will rain is 0.11 and the probability that the flight will be delayed is 0.14. The probability that it will not rain and the flight will leave on time is 0.76. What is the probability that the flight would be delayed when it is raining? Round your answer to the nearest thousandth.
Answers
Since probabilities cannot be negative, we can conclude that the given probabilities are inconsistent or there might be an error in the information provided. Please verify the values and provide correct probabilities so that we can accurately calculate P(B|A), the probability of the flight being delayed when it is raining.
Let's denote the events as follows:
A: It will rain
B: The flight will be delayed
We are given the following probabilities:
P(A) = 0.11 (probability of rain)
P(B) = 0.14 (probability of flight delay)
P(A'∩B') = 0.76 (probability of no rain and on-time departure)
We can use the probability formula to calculate the probability of the flight being delayed when it is raining, P(B|A), which is the probability of B given A.
We know that:
P(B|A) = P(A∩B) / P(A)
To find P(A∩B), we can use the formula:
P(A∩B) = P(A) - P(A'∩B')
Substituting the given values:
P(A∩B) = P(A) - P(A'∩B')
P(A∩B) = 0.11 - 0.76
P(A∩B) = -0.65
for similar questions on probability.
https://brainly.com/question/251701
#SPJ8
Multiply and simplify if possible - radical functions. Thank you!
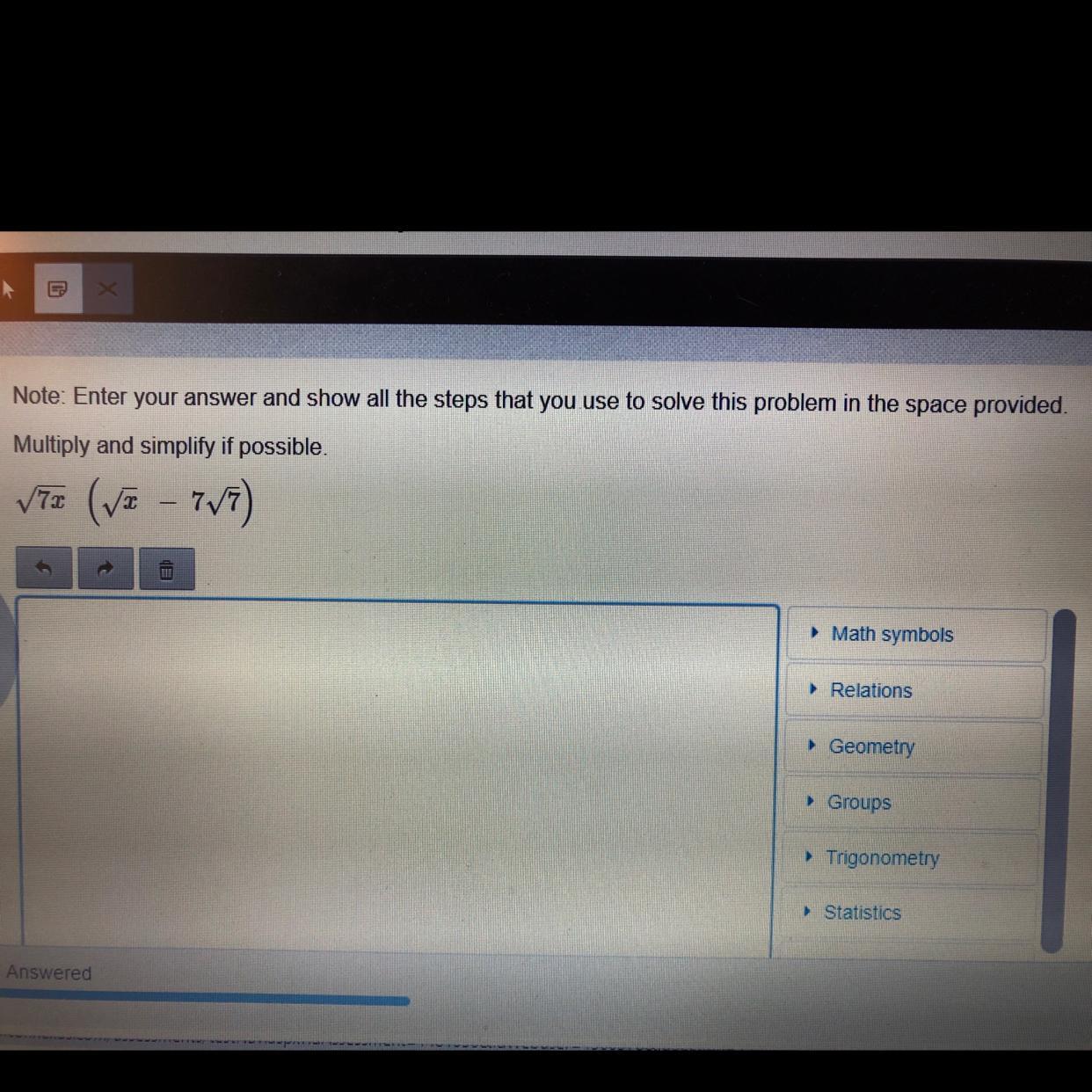
Answers
We want to simplify the following expression
\(\sqrt{7x}(\sqrt{x}+7\sqrt{7})\)First, we can apply the distributive rule to rewrite this product
\(\sqrt{7x}(\sqrt{x}+7\sqrt{7})=(\sqrt{7x})(\sqrt{x})+(\sqrt{7x})(7\sqrt{7})\)Then, using the following property
\(\sqrt{x}\cdot\sqrt{y}=\sqrt{x\cdot y}\)we can rewrite our expression as
\((\sqrt{7x})(\sqrt{x})+(\sqrt{7x})(7\sqrt{7})=\sqrt{7x\cdot x}+7\sqrt{7x\cdot7}\)We can remove the squared terms out of the root
\(\sqrt{7x\cdot x}+7\sqrt{7x\cdot7}=x\sqrt{7}+7\cdot7\sqrt{x}=x\sqrt{7}+49\sqrt{x}\)and this is our answer.
\(\sqrt{7x}(\sqrt{x}+7\sqrt{7})=x\sqrt{7}+49\sqrt{x}\)Minimize f(x)=2x2 1-2 x1 x 2+2x2-6 x 1 +6
Subject to: x1+x2-2=0
Using the Lagrange multipliers technique. Compute the optimal point values for x1, x2, l y ll
In an optimization problem with equality constraints, what is the meaning of the values of the Lagrange multipliers?
Answers
The optimal point values for x1, x2, λ, and μ (Lagrange multipliers) in the given problem are:
x1 = 1
x2 = 1
λ = -4
μ = 2
To solve the optimization problem using the Lagrange multipliers technique, we first construct the Lagrangian function L(x1, x2, λ) by incorporating the equality constraint:
L(x1, x2, λ) = f(x1, x2) - λ(g(x1, x2))
Where f(x1, x2) is the objective function, g(x1, x2) is the equality constraint, and λ is the Lagrange multiplier.
In this case, the objective function is f(x1, x2) = 2x1^2 - 2x1x2 + 2x2 - 6x1 + 6, and the equality constraint is g(x1, x2) = x1 + x2 - 2.
The Lagrangian function becomes:
L(x1, x2, λ) = 2x1^2 - 2x1x2 + 2x2 - 6x1 + 6 - λ(x1 + x2 - 2)
To find the optimal values, we need to find the critical points by taking partial derivatives of L with respect to x1, x2, and λ and setting them equal to zero. Solving these equations simultaneously, we get:
∂L/∂x1 = 4x1 - 2x2 - 6 - λ = 0
∂L/∂x2 = -2x1 + 2 + λ = 0
∂L/∂λ = -(x1 + x2 - 2) = 0
Solving these equations, we find x1 = 1, x2 = 1, and λ = -4. Substituting these values into the equality constraint, we can solve for μ:
x1 + x2 - 2 = 1 + 1 - 2 = 0
Therefore, μ = 2.
The optimal point values for the variables in the optimization problem are x1 = 1, x2 = 1, λ = -4, and μ = 2. The Lagrange multipliers λ and μ represent the rates of change of the objective function and the equality constraint, respectively, with respect to the variables. They provide insights into the sensitivity of the objective function to changes in the constraints and can indicate the impact of relaxing or tightening the constraints on the optimal solution. In this case, the Lagrange multiplier λ of -4 indicates that a small increase in the equality constraint (x1 + x2 - 2) would result in a decrease in the objective function value. The Lagrange multiplier μ of 2 indicates the shadow price or the marginal cost of satisfying the equality constraint.
To know more about optimal point values visit:
https://brainly.com/question/9429432
#SPJ11
Kevin buys
A total of 350 raffle tickets are sold.
One of these tickets will win the raffle.
Each ticket has an equal chance of winning the raffle,
Write down the probability that
Kevin's ticket will win the raffle.
Answers
Answer:
1:350 i think
Step-by-step explanation:
i could be wrong
Answer:
1:350 or 1 out of 350. There are 350 tickets, he only bought 1.
At a sand and gravel plant, sand is falling off a conveyor and onto a conical pile at a rate of 12 cubic feet per minute. The diameter of the base of the cone is approximately 4 times the altitude. At what rate is the height of the pile changing when the pile is 18 feet high? Express your answer in terms of π (V=1/3 πr^2h)
Answers
The rate at which the height of the pile is changing when the pile is 18 feet high is given by dh/dt = [Answer] ft/min. sand is falling off the conveyor at a rate of 12 cubic feet per minute,
To find the rate at which the height of the pile is changing, we need to use related rates and the volume formula for a cone. The problem provides information about the rate at which sand is falling ,
off the conveyor, which corresponds to the rate of change of volume of the cone. We also know the relationship between the diameter and altitude of the cone.
Let's denote the height of the pile as h and the radius of the base as r. From the problem statement, we have the relationship r = h/4, since the diameter of the base is approximately 4 times the altitude.
The volume of a cone is given by the formula V = (1/3) * π * r^2 * h. We want to find dh/dt, the rate at which the height is changing, when h = 18 feet.
To solve this problem, we'll differentiate the volume formula with respect to time t, using the chain rule and related rates. We havedV/dt = (1/3) * π * (2rh * dr/dt + r^2 * dh/dt) Since sand is falling off the conveyor at a rate of 12 cubic feet per minute,
we know that dV/dt = 12 ft^3/min. Substituting the given values and the relationship between r and h, we can solve for dh/dt.
Plugging in the values, we have:
12 = (1/3) * π * [(2 * (h/4) * dr/dt) + ((h/4)^2 * dh/dt)]
Simplifying the equation and solving for dh/dt, we can determine the rate at which the height of the pile is changing.
Therefore, the rate at which the height of the pile is changing when the pile is 18 feet high is given by dh/dt = [Answer] ft/min.
Learn more about diameter here:
brainly.com/question/32968193
#SPJ11
Tineka has a sack that contains 7/12 lb of jellybeans. If she splits the jellybeans into 2 piles of equal weight, how much will each pile weigh?
F 3/16
H 1 1/16
G 7/24
J Not here
Answers
The weight of each of the two piles Tineka split the jellybeans in the sack to is 7/24 lb.
What is the weight of each pile?
Division is when two numbers are grouped into equal parts using another number. The sign used to denote division is ÷.
In order to determine the weight of each pile, divide the weight of the sack by 2.
Weight of each sack = 7/12 ÷ 2
7/12 x 1/2 = 7/24
To learn more about division, please check: https://brainly.com/question/13281206
a quality control expert at life batteries wants to test their new batteries. the design engineer claims they have a variance of 8100 with a mean life of 1192 minutes. if the claim is true, in a sample of 72 batteries, what is the probability that the mean battery life would be greater than 1173.8 minutes? round your answer to four decimal places.
Answers
For a sample of 72 batteries, the probability that the average battery life of the sample exceeds 1173.8 minutes is 0.9918.
It states a battery life variance of 8100 minutes and a median battery life of 1192 minutes.
In a sample of 72 batteries, find the probability that the average battery life (x) of the sample exceeds 1173.8 minutes.
Due to the large sample size (n = 72), we can use the central limit theorem to assume that the sample mean follows a normal distribution with mean μ = 1192 and standard deviation σ = sqrt(8100/72) = 30.
So the z-score for x= 1173.8 is
z = (x - μ) / (σ / sqrt(n))
= (1173.8 - 1192) / (30 / square(72))
= -2.4
You can use a standard normal distribution table or calculator to find the probability that a standard normal random variable is greater than -2.4. This is 0.9918 (rounded to four decimal places).
Therefore, for a sample of 72 batteries, the probability that the average battery life of the sample exceeds 1173.8 minutes is 0.9918 (rounded to four decimal places) if the claim is correct.
learn more about the probability
brainly.com/question/30034780
#SPJ4
There is a probablity of ____ that any individual at a random from
a population will fall (plus or minus) one standard deviation of
the mean.
Answers
Step-by-step explanation:
I hope this answer is helpful ):

The critical value in a chi-square test for independence depends on Multiple Choice the normality of the data. the variance of the data. the number of categories. the expected frequencies.
Answers
The critical value in a chi-square test for independence depends on the number of categories and expected frequencies, and not on the normality or variance of the data.
The critical value in a chi-square test for independence is determined by the number of categories and expected frequencies in the data. This test is used to analyze the relationship between two categorical variables, and the expected frequencies are calculated based on the assumption of independence between these variables. The critical value is the minimum value of the test statistic that would result in rejecting the null hypothesis, which states that the two variables are independent.
The normality and variance of the data do not affect the critical value in a chi-square test for independence. This test does not assume a normal distribution of the data, and the variance is not used to calculate the expected frequencies. Instead, the expected frequencies are determined by the marginal frequencies of the two variables, assuming that they are independent.
It is important to use the correct critical value in a chi-square test for independence, as using the wrong value could result in incorrect conclusions about the relationship between the two variables. The critical value can be found using a chi-square distribution table or calculator, based on the number of categories and the level of significance chosen for the test.
Know more about critical value here:
https://brainly.com/question/30168469
#SPJ11
A source supply produces 7.5 x 107 gallons of water per day. How many gallons of water will be produced in 37 days?
Answers
Answer: 29,692.5 gallons of water
Step-by-step explanation: first i multiplied 7.5 and 107 and got 802.5 and since it wanted to know about 37 days i multiplied 802.5 by 37 and got 29,692.5
How do you find the third side of an inequality of a triangle?
Answers
To find the third side of an inequality of a triangle, you must first use the Triangle Inequality Theorem.
This theorem states that for any triangle, the sum of any two sides of the triangle must be greater than the third side. This means that in order to find the length of the third side, you must subtract the sum of the two known sides from the smaller of the two sides, then the length of the third side will be equal to the difference between these two numbers. For example, if two sides of a triangle have lengths of 4 and 3, the third side must be greater than 1 (4 + 3 = 7 and 4 - 3 = 1). Therefore, the length of the third side must be greater than 1.
Learn more about Triangle Inequality Theorem here:
https://brainly.com/question/1163433
#SPJ4
[3 + 3 + 3 + 3 pts) In this exercise you will generalize the binomial distribution.
(a) Show that the number of possible ways in which a set A with cardinality |A| = n can be partitioned into r subsets A1,..., A, with cardinalities n1,..., nr such that ni +...+ nor = n is equal to n! / ni!...n!
Answers
The number of possible ways to partition a set A with cardinality n into r subsets with varying cardinalities is given by n! / (n1! * n2! * ... * nr!).
How can a set A be partitioned into subsets of different sizes?Partitioning a set A into subsets of varying sizes involves calculating the number of possible ways to arrange the elements in the subsets. The formula n! / (n1! * n2! * ... * nr!) accounts for the total number of permutations while considering the specific sizes of each subset.
To understand why this formula works, let's break it down step by step.
Step 1: Counting permutations
The numerator n! represents the total number of permutations of the elements in set A. This is because when we partition a set, the order in which we choose the elements for each subset matters. So, we start with n choices for the first element, (n-1) choices for the second element, and so on, resulting in n! permutations.
Step 2: Accounting for subsets
However, in the numerator, we are overcounting because the order of elements within each subset doesn't matter. To correct for this, we divide by the factorials of the sizes of the subsets (n1!, n2!, ..., nr!). This ensures that each partition is counted only once, irrespective of the order in which the elements are chosen within each subset.
Step 3: Simplifying the formula
Dividing n! by the product of the factorials simplifies the formula, giving us the final result: n! / (n1! * n2! * ... * nr!).
Learn more about subsets
brainly.com/question/28705656
#SPJ11
Fill in the blanks with the correct words:
An event that has probability O is said to be
An event that has probability 1 is said to be
Answers
Answer:
Impossible; certain to happen
Step-by-step explanation:
Probability = 0 applies to an event which cannot happen. Example: roll a die and get a 7.
Probability = 1 applies to an even which is certain to occur. Example: roll a die and get a number less than 8.
The volume of this cone is 140 cm3
Find the perpendicular height, c.
Give your answer rounded to 1 DP.
х
7 cm

Answers
Answer:
x = 10.9 cm
Step-by-step explanation:
Formula for a cone
Volume (cone) = 1/3 × π × (radius)² × heightHere, we are given :
Diameter = 7 cmVolume = 140 cm³Solving
140 = 1/3 × 22/7 × (7/2)² × (x)420 = 11 × 7/2 × (x)77x = 840x = 840/77x = 10.9 cm (1 DP)Answer:
x ≈ 3.6 cm
Step-by-step explanation:
the volume (V) of a cone is calculated as
V = πr²h ( r is the radius and h the perpendicular height )
here diameter = 7 , so r = 7 ÷ 2 = 3.5 , V = 140 and h = x , then
π × 3.5² × x = 140
π × 12.25x = 140 ( divide both sides by 12.25π )
x = \(\frac{140}{12.25\pi }\) ≈ 3.6 cm ( to 1 dec. place )
Solve -6x +18> -30.
A. x < 2
B. x > 2
C. x > 8
D. x < 8
Answers
Answer: D, x < 8
Step-by-step explanation: Subtract 18 from both sides.
Simplify the expression
Subtract the numbers
Subtract the numbers
Divide both sides by the same factor, and flip the relation because the factor is negative
Cancel terms that are in both the numerator and denominator
Divide the numbers
−6x+18−18>−30−18=
=x<8
What is the area of this kite?
8 m
12 m
12 m
30 m
38 m
Answers
Write a real word situation involving multiplication comparison that may be represented by the equations shown 24=4times6;24=6 times 2. 45=9 times 5; 45 = 5 times 9 3. 36= 3 times12; 36 =12 times 3 4. 60 =12 times 5; 60 = 5times 12

Answers
1. 24=4times6;24=6 times 4 is represented by apple orchard
2. 45=9 times 5; 45 = 5 times 9 is represented by classroom of students
3. 36= 3 times12; 36 =12 times 3 is represented by A construction site
4. 60 =12 times 5; 60 = 5times 12 is represented by A grocery store
How write the real word situation1. An apple orchard is comparing the productivity of two of its workers in terms of the number of baskets of apples picked. Worker A picked 4 baskets in 6 hours, while Worker B picked 6 baskets in 2 hours.
The situation can be represented by the equations 24 = 4 x 6 and 24 = 6 x 2, where 24 represents the total number of baskets picked.
2. Another example is a classroom of students comparing the number of pencils each student has. In one row, there are 9 students and each student has 5 pencils. In another row, there are 5 students and each student has 9 pencils. This situation can be represented by the equations 45 = 9 x 5 and 45 = 5 x 9, where 45 represents the total number of pencils in each row.
3. A construction site is comparing the efficiency of two workers in terms of the number of bricks they can lay in a certain amount of time. Worker A can lay 3 bricks in 12 minutes, while Worker B can lay 12 bricks in 3 minutes. The situation can be represented by the equations 36 = 3 x 12 and 36 = 12 x 3, where 36 represents the total number of bricks laid.
4. A grocery store is comparing the size of two crates of oranges. Crate A contains 12 rows of oranges, with 5 oranges in each row. Crate B contains 5 rows of oranges, with 12 oranges in each row. This situation can be represented by the equations 60 = 12 x 5 and 60 = 5 x 12, where 60 represents the total number of oranges in each crate.
Read more on multiplicative properties here https://brainly.com/question/615813
#SPJ1
Cynthia's older cousin sold her his collection of Pokemon cards. She paid him $9.50 and he charged her $0.10 per card. How many Pokemon cards did she buy?
Answers
Answer:
95$
Step-by-step explanation:
Choose one answer is math
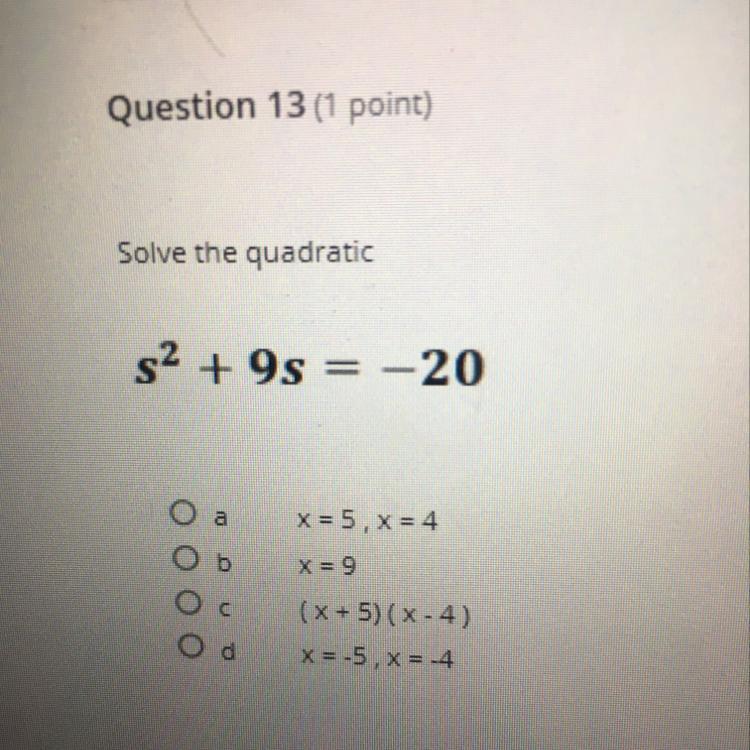
Answers
the answer is d which is x=.5x=-4
Create ABC by drawing AC. AC represents the foreman’s line of sight to the top of the landfill. What is m
Answers
Where the above is given, the required angle m∠BAC = 45°.
In triangle ABC. AC represents the foreman’s line of sight to the top of the landfill. Landfill height is BC
What is triangle?The triangle is geometric shape which includes 3 sides and sum of interior angle should not grater than 180°
According to conditions angle b = 90°
The sum of angles of a triangle= 180°
That is a + b + c = 180
Therefore, c = a
a = (180 - b)/2
= (180 - 90) / 2
= 90 / 2
= 45°
Hence, the required angle m∠BAC = 45°
Learn more about triangles at:
brainly.com/question/273823
#SPJ1
Full Question:
Although part of your question is missing, you might be referring to this full question:
Question 1 Create Triangle ABC by drawing AC. Segment AC represents the foreman’s line of sight to the top of the landfill. What is Angle m BAC?
Alex is feeling stressed this morning. He did not get enough sleep because a dog barked most of the night. The dog barked from 11;41p.m. until 12:09 a.m.Then it started barking again at 3:35 a.m. and didn’t stop until 4:10 a.m.How long did the dog bark in all?
Answers
Answer:
Poor Alex, I know how they feel, I got a dog myself.
The amount of time between
11:41 pm to 12:09 am is
19 minutes (to 12 am, 60 minutes to next hour) + 9
which is 28 minutes for the first dog barking session
the second time is 35 minutes,
using same method as before.
adding the two separte barking sessions we get
35+28= 63 minutes
which is equivelant to 1 hour and 3 minutes.
In conclusion the dog barks for 1 hour and 3 minutes in total.
PROBLEM 3: Sales tax in a certain community is 7%. If the sales tax on a new car was $1400, what was the selling price of the car? Rephrase: $1400 is 7% of what number?
Answers
Answer:
$20,000
Step-by-step explanation:
Let the new car price before tax be p. If the sales tax was $1400, then the following is true: 0.07p = $1400, and p = $20,000
$1400 is 7% of the before-tax new car price, which is $20,000
2a2 + cb; a = 5, b = 11, and c = 3
Answers
53
Explanation
Calculate the product
20+3•11
Multiply the numbers
20+30
Add the numbers
53
Answer:
83 is the answer
Step-by-step explanation:
2*5^2+33
2*25+33
50+33=83
Which is more, 8 pints or 13 cups?
Answers
Answer:
8 pints
Step-by-step explanation:
A pint is 16 ounces = 2 cups
8 pints is then 16 cups
what would the method be???

Answers
Answer:
The AA method
Step-by-step explanation:
The AA method states that if 2 of a triangle's angles are congruent to that of another triangle's 2 angles, then those triangles are similar.
PLEASE MARK BRAINLIEST!!!
The mass of a substance varies directly as the volume of the substance. If a mass of 30 kg of a substance has a volume of 6 liters, what is the volume of 65 kg of the substance?
Answers
Answer:
The volume of 65 kg of the substance is 13 liters.
Step-by-step explanation:
If a substance's mass varies directly from its volume, it means that the ratio of mass to volume remains constant. In this case, we can calculate the continuous ratio and then use it to find the volume.
Given:
Mass1 = 30 kg
Volume1 = 6 liters
Let's denote the constant ratio as k.
Mass1 / Volume1 = k
30 kg / 6 liters = k
k = 5 kg/liter
Now, we can find the volume2 for a mass of 65 kg using the constant ratio:
Mass2 = 65 kg
Volume2 = ?
Mass2 / Volume2 = k
65 kg / Volume2 = 5 kg/liter
To find Volume2, we can cross multiply:
65 kg = 5 kg/liter * Volume2
Volume2 = 65 kg / 5 kg/liter
Volume2 = 13 liters