Principal: $4,000
Rate: 7.25%
Time: 8 years
How much money will need to be paid back to the bank for this loan?
Answers
Answer:
the money required to pay back to the bank for the loan is $7,002
Step-by-step explanation:
The computation of the money required to pay back to the bank for the loan is given below:
= Principal × (1 + rate of interest)^number of years
= $4,000 × (1 + 0.0725)^8
= $4,000 × 1.0725^8
= $7,002
Hence, the money required to pay back to the bank for the loan is $7,002
Related Questions
How can you write the expression 7(b-2) in words?
OA
two subtracted from the quotient of seven divided by b
ОВ,
seven added to difference of b minus two
OC. the quotient of seven divided by b minus two
OD
two subtracted from seven times b
O E, the product of seven and the difference of b minus two
Answers
Answer:
E (The product of seven and the difference of b minus two)
Step-by-step explanation:
Help with this question plzz

Answers
Answer:
I think it is 4 white and 3 blue
Step-by-step explanation:
Because they have 3 cups of white then 6 cups of white so i think they multiplied it. Then they have 4 cups of blue then 8 cups of blue. So if you multiply it, it will give you the answer. I hope this is right and it helped and can you mark me brainliest!!!!!!!!
Consider the original trapezoid and the reduction. A trapezoid has corresponding side lengths of 13. 5 centimeters and 9 centimeters. Side A corresponds to a side with length 3 centimeters. Figures not drawn to scale. What is the length of side A, in centimeters, on the reduced trapezoid? 1 1. 5 2 2004. 5.
Answers
Answer:
Consider the original trapezoid and the reduction. A trapezoid has corresponding side lengths of 13. 5 centimeters and 9 centimeters. Side A corresponds to a side with length 3 centimeters. Figures not drawn to scale. What is the length of side A, in centimeters, on the reduced trapezoid? 1 1. 5 2 2004. 5.
Step-by-step explanation:
What is Solve 7y ≤ 33 + 4y
Answers
Answer:
y ≤ 11
Step-by-step explanation:
7y ≤ 33 + 4y
3y ≤ 33
y ≤ 11
So, the answer is y ≤ 11
The same eight people sit in a certain church pew every week, but not always in the same order. Every week, each person hugs the people immediately to his or her left and right. How many weeks does it take (at a minimum) for every pair of people to hug at least once
Answers
It takes 4 weeks at minimum for each pair to hug at least once if they sit in random order.
Analyzing the Given Information
As per the given information,
Number of people = 8
It is given that they sit in random order every week.
W e assume that the order is not repeated.
There are 4 pairs and since a person hugs both the persons on his immediate left and right.
Determining the Number of Weeks
Total number of people to be hugged by each person = 7
Number of people hugged by a person in one week = 2
So, number of weeks taken by each to huge every other person = 7/2
⇒ It will take (3 +1) for every pair to hug.
It takes 4 weeks at a minimum for every pair to hug if we assume that their order is not repeated.
Learn more about order here:
https://brainly.com/question/10952560
#SPJ4
please help
Stay safe and healthy

Answers
Answer:
9 No explanation needed
-x+2y=11 on a graph plz help
Answers
Answer:
Hope this helps.

Guys i rlly need help im getting an F on this can someone please help me :(

Answers
Answer:
THE SLOPE OF THE GRAPH
Step-by-step explanation:
Answer:
the slope of the graph of y = mx+b
Step-by-step explanation
The equation of any straight line can be written as: y = mx + b, where m is the slope of the line and b is the y-intercept.
The equation y=0.06x+105 gives the cost y of renting a car if the care is driven x miles. Based on this equation, for every mile the car is driven the cost of increases by how much?
Answers
Answer:
it increases by 6 cents for every mile driven plus the initial 105 dollars
Step-by-step explanation:
brainliest plzzzz
if u and v are in r n , how are uvt and vut related?
Answers
The vectors uvt and vut are related by a simple matrix transposition.
In other words, if we consider u, v, and t as columns of a matrix, say A, then uvt is simply the product of A and the vector [1 0 1] (a column vector with 1's in the first and third rows and 0 in the second row).
On the other hand, vut is the product of the transposed matrix of A (denoted as A^T) and the vector [1 0 1]. Therefore, uvt and vut are related as follows:
vut = (A^T) [1 0 1]
In summary, uvt and vut are related through a matrix transposition, with vut being the product of the transposed matrix of A and the vector [1 0 1].
For more questions like Vectors click the link below:
https://brainly.com/question/22862757
#SPJ11
Triangles P and Q are similar.
Find the lengths of the sides:
A
P
7cm
с
6cm
B
X
The diagram is not drawn to scale.
18cm
Q
N
9cm
Answers
The lengths of the sides are: AP = 7cm BC = 6cm BX = 28/3 cm and
QN = 12cm.
What is the triangle?A triangle is a three-sided polygon with three angles. It is a fundamental geometric shape and is often used in geometry and trigonometry.
Since triangles P and Q are similar, their corresponding sides are proportional. That means:
AP/PN = BX/QN
We know that AP = 7cm and PN = 9cm, so we can substitute those values:
7/9 = BX/QN
We also know that QC = 6cm, so we can find QN by subtracting CN from QC:
QN = QC - CN
QN = 18cm - 6cm
QN = 12cm
Now we can solve for BX:
7/9 = BX/12
Multiplying both sides by 12, we get:
BX = 84/9
Simplifying, we get:
BX = 28/3 cm
Therefore, the lengths of the sides are:
AP = 7cm
BC = 6cm
BX = 28/3 cm
QN = 12cm
To learn more about triangles from the given link:
https://brainly.com/question/2773823
#SPJ1
Complete question:

Determine which equation is false, based on the solution set S:{2}.
7 = 6p − 5
4t = 8
3(3c + 1) = 21
5m + 8 = 16
pls help ill give 45 points
Answers
Answer:
\(5m+8=16\)
Step-by-step explanation:
\(5m+8=16 \\ \\ 5m=8 \\ \\ m=1.6 \neq 2\)
Sandy and Tom went for a run. Sandy started running 12 seconds before Tom. Sandy runs 7 meter per second. Tom runs 9 meters per second. How long did it take for both Sandy and Tom to cover the same distance?
Answers
It took both Sandy and Tom 54 seconds to cover the same distance.
To solve this problemWe can set up an equation based on their relative speed
Take the supposition that Tom needs "t" seconds to travel the distance. Sandy started jogging 12 seconds before Tom, so it will take her "t + 12" seconds longer to complete the same distance.
To determine the distance traveled by Sandy, multiply her speed (7 meters per second) by her time (t + 12) seconds. Tom's distance traveled may be determined by dividing his speed (9 meters per second) by his time (t) seconds.
Equating the distances covered by Sandy and Tom:
7(t + 12) = 9t
Expanding the equation:
7t + 84 = 9t
Subtracting 7t from both sides:
84 = 2t
Dividing both sides by 2:
t = 42
Tom traveled the distance in 42 seconds as a result. We add the 12-second lead Sandy had to determine the time it took for both Sandy and Tom to travel the same distance:
t + 12 = 42 + 12 = 54
So, it took both Sandy and Tom 54 seconds to cover the same distance.
Learn more about equation here : brainly.com/question/13763238
#SPJ1
help please sorry it’s blurry

Answers
Answer:
z = -70
Explanation:
-12.2z-13.4z=1792
-25.6z=1792
Divide both sides by (-25.6)
z = -70
10. Set up and evaluate the definite integral for the area of the surface generated by revolving the curve a) (3 pts.)y= 6x 3+ 2x1 ,1≤x≤2, about the x-axis; b) (3 pts.) x= 4y−1,1≤y≤4, about the y-axis.
Answers
The definite integral for the area of the surface generated by revolving the curve y = 6x^3 + 2x about the x-axis, over the interval 1 ≤ x ≤ 2, can be set up and evaluated as follows:
∫[1 to 2] 2πy √(1 + (dy/dx)^2) dx
To calculate dy/dx, we differentiate the given equation:
dy/dx = 18x^2 + 2
Substituting this back into the integral, we have:
∫[1 to 2] 2π(6x^3 + 2x) √(1 + (18x^2 + 2)^2) dx
Evaluating this definite integral will provide the surface area generated by revolving the curve about the x-axis.
b) The definite integral for the area of the surface generated by revolving the curve x = 4y - 1 about the y-axis, over the interval 1 ≤ y ≤ 4, can be set up and evaluated as follows:
∫[1 to 4] 2πx √(1 + (dx/dy)^2) dy
To calculate dx/dy, we differentiate the given equation:
dx/dy = 4
Substituting this back into the integral, we have:
∫[1 to 4] 2π(4y - 1) √(1 + 4^2) dy
Evaluating this definite integral will provide the surface area generated by revolving the curve about the y-axis.
By setting up and evaluating the definite integrals for the given curves, we can find the surface areas generated by revolving them about the respective axes. The integration process involves finding the appropriate differentials and applying the fundamental principles of calculus.
To know more about integral follow the link:
https://brainly.com/question/33191486
#SPJ11
Driving under the influence of alcohol (DUI) is a serious offense. The following data give the ages of a random sample of 50 drivers arrested while driving under the influence of alcohol. This distribution is based on the age distribution of DUI arrests given in the Statistical Abstract of the United States (112th Edition). 46 16 41 26 22 33 30 22 36 34 63 21 26 18 27 24 31 38 26 55 31 47 27 43 35 22 64 40 58 20 49 37 53 25 29 32 23 49 39 40 24 56 30 51 21 45 27 34 47 35 (a) Make a stem-and-leaf display of the age distribution. (Use the tens digit as the stem and the ones digit as the leaf. Enter numbers from smallest to largest separated by spaces. Enter NONE for stems with no values. )
Answers
To make a stem-and-leaf display, we will separate the ages into stems based on the tens digit and leaves based on the ones digit.
Therefore, the stem-and-leaf display of the age distribution is:
1 | 6
2 | 6 8 9
3 | 3 7 8
4 | 1 3 6 7 8 9
5 | 3 5
6 | 3 4 5 8
A stem-and-leaf display is a graphical representation of a set of data. It is a way to organize and display data in a way that allows for easy interpretation and comparison of the data.
In a stem-and-leaf display, the data is separated into two parts: the stem and the leaf. The stem represents the tens digit of each data point, and the leaf represents the ones digit. For example, the number 47 would be represented as a stem of 4 and a leaf of 7.
The stems are listed vertically, and the leaves are listed horizontally next to their respective stems. The leaves are usually listed in increasing order.
Learn more about Standard Distribution here:
https://brainly.com/question/27275125
#SPJ4
Which angles are supplementary?
PKO and ∠PKL
angle P K O, and , angle P K L
∠MKN and ∠OKN
angle M K N, and , angle O K N
∠LKM and ∠MKN
angle L K M, and , angle M K N
∠PKO and ∠MKN

Answers
Answer:
angle mkn and okn
Step-by-step explanation:
beacuse both of them are 90 degree to each other and hence the sum of two 90 degree angle is 180 which is supplementary
A rectangular prism has a length of 13 meters, a height of 18 meters, and a width of 5 meters.
What is its volume, in cubic meters?
Answers
Answer:
1170 m^3
Step-by-step explanation:
Just compute 13x18x5. The formula for volume of a rectangular prism is length times width times height.
Part C
What is the equation represented by the graph?

Answers
to get the equation of any straight line, we simply need two points off of it, let's use those two in the picture below
\((\stackrel{x_1}{1}~,~\stackrel{y_1}{8})\qquad (\stackrel{x_2}{3}~,~\stackrel{y_2}{24}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{24}-\stackrel{y1}{8}}}{\underset{\textit{\large run}} {\underset{x_2}{3}-\underset{x_1}{1}}} \implies \cfrac{ 16 }{ 2 } \implies 8\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{8}=\stackrel{m}{ 8}(x-\stackrel{x_1}{1}) \\\\\\ y-8=8x-8\implies {\Large \begin{array}{llll} y=8x \end{array}}\)

Answer:
\(y=8x\)
Step-by-step explanation:
We can see that this line has a constant of proportionality. That is — x is proportional to y and vice versa. This means that the equation for the line's equation will be in the form:
\(y = mx\)
where \(m\) is the ratio of x to y.
This ratio is also known as the line's slope. We can solve for the slope using the equation:
slope = rise / run
slope = \(\Delta\)y / \(\Delta\)x
slope = 8 / 1
slope = 8
\(m=8\)
So, the equation of the line is:
\(y=mx\)
\(\boxed{y=8x}\)
what is 24 – ( n + 3 ) ÷ 2 when n = ?
Answers
Answer:
16 or 8
Step-by-step explanation:
I'm not sure if this are right
Solve for x. 3x - 4 = 2x - 10
a. x= -6
b. x= 14
c. x= -14
d. x= 6
Answers
Answer:
x=-6
Step-by-step explanation:
f(x)=2x-6 answer please
Answers
Answer:
well that's already the slope and your i-intercept would be -6
Step-by-step explanation:
Deanna will cook a turkey for about 15 minutes per pound of turkey.
If she bought an 11-pound turkey, how long should she cook it for, in minutes?
Answers
Answer:
165 minutes is how long it would take
Answer:
11×15
lbs× minutes per lbs
True or folse: When F(-2. - 7) is rotated 180° about(-1,5), the image is located at F'(0, 17).
O True
O False
Answers
Answer:
tru
Step-by-step explanation:
Given 5000 carrots, it is said that carrots length, x,is normally distributed with (mean =11.5cm and standard deviation =1.15cm). of the 5000 carrots measured how many are between 10 cm and 13 cm
Answers
it is estimated that approximately 4032 carrots out of the 5000 measured fall between 10 cm and 13 cm in length.
To calculate the estimated number of carrots between 10 cm and 13 cm, we need the values of z1 and z2. Let's calculate them:
Lower bound:
z1 = (10 - 11.5) / 1.15 = -1.3043
Upper bound:
z2 = (13 - 11.5) / 1.15 = 1.3043
Using a standard normal distribution table or a calculator, we can find the probabilities associated with these z-scores.
P(Z < -1.3043) ≈ 0.0968
P(Z < 1.3043) ≈ 0.9032
To find the probability of a carrot falling between 10 cm and 13 cm, we subtract the lower probability from the upper probability:
P(-1.3043 < Z < 1.3043) ≈ 0.9032 - 0.0968 ≈ 0.8064
Finally, we multiply this probability by the total number of carrots (5000) to estimate the number of carrots between 10 cm and 13 cm:
Estimated number of carrots = 0.8064 * 5000 ≈ 4032
Therefore, it is estimated that approximately 4032 carrots out of the 5000 measured fall between 10 cm and 13 cm in length.
to more about Probability visit:
brainly.com/question/32117953
#SPJ11
Is the quantity represented by x is a function that changes over time ie is not constant true or false?
Answers
The given statement "the quantity represented by x is a function that changes over time i.e. is not constant" is false.
The statement "the quantity represented by x is a function that changes over time i.e. is not constant" is not true. A function is a set of ordered pairs of numbers (x, y) such that each x corresponds to exactly one y value.
In other words, for a given value of x, there is only one corresponding value of y, which implies that it cannot change over time. Therefore, if x is a function, it is constant. Hence the statement is false.
Conclusion :The given statement "the quantity represented by x is a function that changes over time i.e. is not constant" is false. A function is a set of ordered pairs of numbers (x, y) such that each x corresponds to exactly one y value. Therefore, if x is a function, it is constant.
To know more about function visit
https://brainly.com/question/21426493
#SPJ11
I just need level two and three solved please

Answers
Answer:
intercepts: (0, 5/2) or (-5, 0)arbitrary point: (7, 6)Step-by-step explanation:
You want two methods of choosing points on the line with slope 1/2 through A(-1, 2).
InterceptsWriting the equation in standard form, we can find the x- and y-intercepts. To get there, we can start from point-slope form:
y -k = m(x -h) . . . . . . line with slope m through point (h, k)
y -2 = 1/2(x -(-1)) . . . . . using given slope and point
2y -4 = x +1 . . . . . . . . . . multiply by 2
x -2y = -5 . . . . . . . . . . . . add -1 -2y
Setting x=0 tells us the y-intercept is ...
0 -2y = -5
y = -5/-2 = 5/2
So, the y-intercept is (0, 5/2).
Setting y=0 tells us the x-intercept is ...
x -2(0) = -5
x = -5
So, the x-intercept is (-5, 0).
Arbitrary pointIt will be convenient to choose an arbitrary y-value to find another point on the line. We can pick y = 6, for example, Then the corresponding x-value is ...
x -2y = -5
x = -5 +2y = -5 +2(6) = 7
Another point on the line is (7, 6).
__
Additional comment
If we were to choose an arbitrary value for x, we would want it to be odd, so the corresponding y-value would be an integer. We chose to pick an arbitrary value of y so we didn't have to worry about how to make the x-value an integer.
<95141404393>

Please help, and thank you in advance.
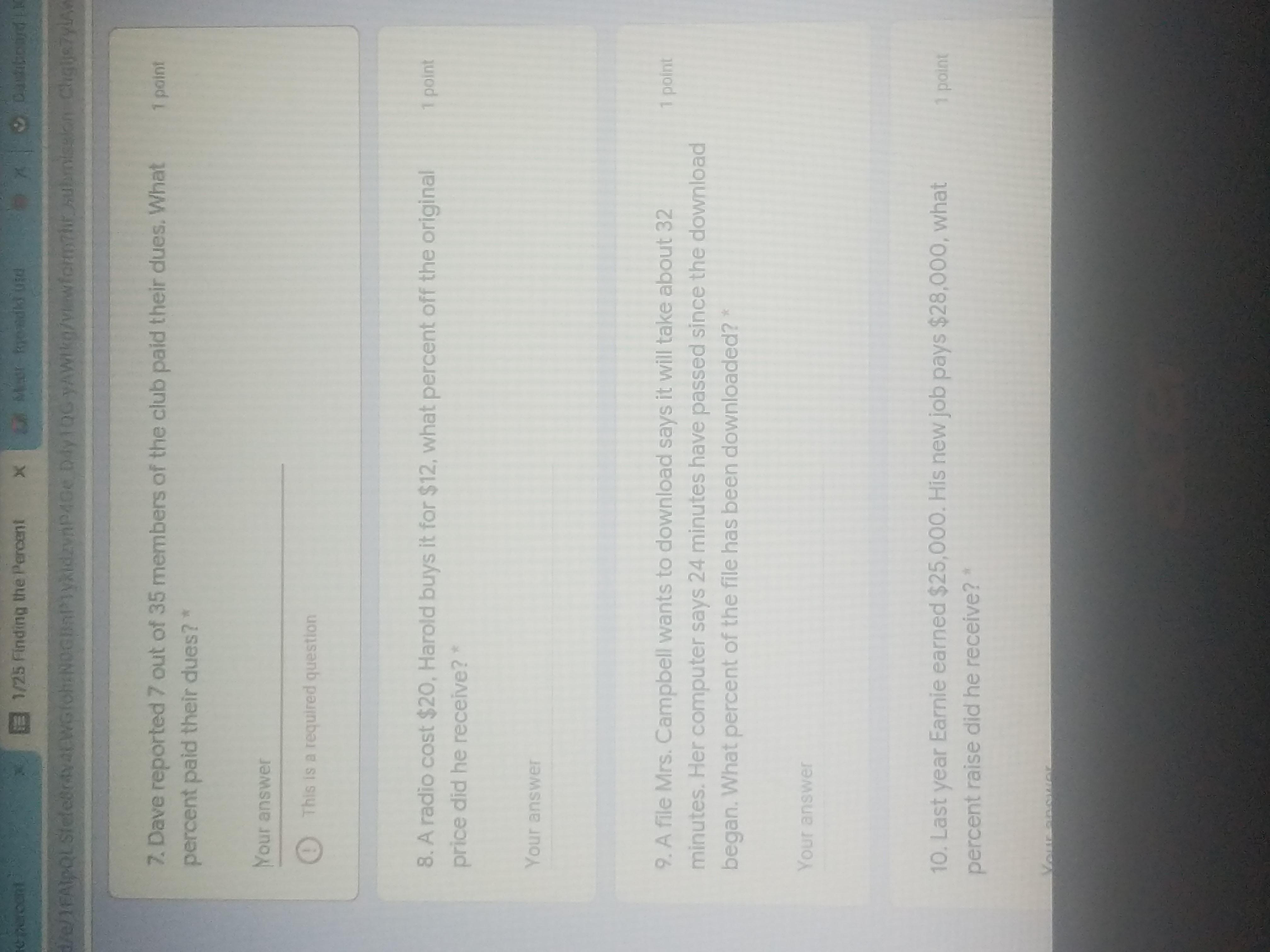
Answers
2) 40%
3) 75%
4) 12%
Find the local maximum and minimum values and saddle points of the function f(x,y)=x3−3x+3xy2f(x,y)=x3−3x+3xy2.
Answers
For the function f(x,y)=x3−3x+3xy2,
(0,0) - a critical point of undetermined nature
(0,1) - a saddle point
(0,-1) - a saddle point
and there are no local maxima or local minima.
To find the local maximum and minimum values and saddle points of the function f(x,y)=x3−3x+3xy2, we need to first find its critical points.
To find the critical points of f(x,y), we need to solve the system of equations given by setting the partial derivatives of f(x,y) with respect to x and y equal to zero:
∂f/∂x = 3x2 - 3 + 3y2 = 0
∂f/∂y = 6xy = 0
From the second equation, we get either x=0 or y=0.
If x=0, then the first equation becomes 3y^2-3=0, which gives y=±1. Substituting these values of x and y back into f(x,y), we get the critical points (0,1) and (0,-1).
If y=0, then the second equation becomes x=0. Substituting this value of x back into f(x,y), we get the critical point (0,0).
So, we have three critical points: (0,0), (0,1), and (0,-1).
Now, we need to classify these critical points as local maxima, local minima, or saddle points. To do this, we can use the second partial derivative test.
The Hessian matrix of f(x,y) is given by:
H(x,y) =
[6x 6y]
[6y 6x+6]
At the critical point (0,0), we have H(0,0) =
[0 0]
[0 6]
The determinant of H(0,0) is 0, and the eigenvalues are 0 and 6. Since the determinant is 0, we cannot conclude whether (0,0) is a local maximum, local minimum, or saddle point using the second partial derivative test. Instead, we can use other methods to determine the nature of this critical point.
At the critical point (0,1), we have H(0,1) =
[0 6]
[6 6]
The determinant of H(0,1) is -36, and the eigenvalues are approximately -4.59 and 10.59. Since the determinant is negative and the eigenvalues have opposite signs, we can conclude that (0,1) is a saddle point.
At the critical point (0,-1), we have H(0,-1) =
[0 -6]
[-6 6]
The determinant of H(0,-1) is 36, and the eigenvalues are approximately -10.59 and 4.59. Since the determinant is positive and the eigenvalues have opposite signs, we can conclude that (0,-1) is also a saddle point.
Therefore, the critical points of f(x,y) are:
(0,0) - a critical point of undetermined nature
(0,1) - a saddle point
(0,-1) - a saddle point
So, there are no local maxima or local minima for the function f(x,y)=x3−3x+3xy2.
For more such questions on Functions.
https://brainly.com/question/31402672#
#SPJ11
You are the marketing manager for Coffee Junction. The revenue for the company is given by R(x)=− 32x 3+6x 2+18x+4 where R(x) is revenue in thousands of dollars and x is the amount spent each month on advertisement, in thousands of dollars. 0≤x≤25 a) At what level of advertising spending does diminishing returns start? Explain What this diminishing returns means for this company. b) How much revenue will the company earn at that level of advertising spending? c) What does 0≤x≤25 tell us with respect to this problem?
Answers
a) Diminishing returns start at x = 1, where the marginal revenue will be less than the marginal cost
b)At x = 1, the company will earn R(1) = -32 + 6 + 18 + 4 = -4,000 dollars.
c) 0 ≤ x ≤ 25 implies that the Coffee Junction company has the capacity to spend a maximum of 25,000 dollars per month on advertisements.
a) At what level of advertising spending does diminishing returns start?
Diminishing returns refers to a situation when the marginal return on investment decreases as more resources are devoted to it. For instance, in case of Coffee Junction, increasing the advertising expenditure may lead to higher revenue, but the marginal revenue (revenue generated by each additional dollar spent) will gradually decrease.
b) How much revenue will the company earn at that level of advertising spending?
At x = 1, the company will earn R(1) = -32 + 6 + 18 + 4 = -4,000 dollars.
c) What does 0≤x≤25 tell us with respect to this problem?
In this problem, 0 ≤ x ≤ 25 implies that the Coffee Junction company has the capacity to spend a maximum of 25,000 dollars per month on advertisements.
To learn more about marginal cost refer:-
https://brainly.com/question/14923834
#SPJ11