Prove : ∣u⋅v∣⩽∣u∣∣v∣
∣u+v∣⩽∣u∣+∣v∣
Answers
Both of the given inequalities (∣u⋅v∣⩽∣u∣∣v∣ and ∣u+v∣⩽∣u∣+∣v∣) have been proved using the Cauchy-Schwarz inequality and the triangle inequality, respectively.
To prove the inequalities, let's consider vectors u and v in a vector space.
Proof: ∣u⋅v∣⩽∣u∣∣v∣
We start by using the Cauchy-Schwarz inequality:
∣u⋅v∣ ⩽ ∣u∣∣v∣
This inequality is a direct consequence of the Cauchy-Schwarz inequality, which states that for any vectors u and v in a vector space:
∣u⋅v∣ ⩽ ∣u∣∣v∣
Therefore, the first inequality is proven.
Proof: ∣u+v∣⩽∣u∣+∣v∣
To prove this inequality, we can use the triangle inequality:
∣u+v∣ ⩽ ∣u∣ + ∣v∣
The triangle inequality states that for any vectors u and v in a vector space:
∣u+v∣ ⩽ ∣u∣ + ∣v∣
Hence, the second inequality is proven.
Both of the given inequalities (∣u⋅v∣⩽∣u∣∣v∣ and ∣u+v∣⩽∣u∣+∣v∣) have been shown to be true using the Cauchy-Schwarz inequality and the triangle inequality, respectively.
To learn more about Cauchy-Schwarz inequality visit:
brainly.com/question/30402486
#SPJ11
Related Questions
20 points please hurry
Ruby is visiting San Francisco. From her hotel she walks 1 block east and 2 blocks south to a coffee shop. Then she walks 2 blocks west and 3 blocks south to a
museum. Where is the museum in relation to her hotel?
The museum is block(s) and block(s) of her hotel.

Answers
Answer:
5 blocks south and 1 block west ( I think that's right sorry if its wrong I'm heading off to bed)
PEASE HELP ASAP
ACB~ EFD
What is x equal to?
Enter your answer in decimal form.

Answers
The value of x in the similar triangles is 11.4.
What are similar triangles?Two triangles are similar if they have the same ratio of corresponding sides and equal pair of corresponding angles.
Similar triangles are the triangles that have corresponding sides in proportion to each other and corresponding angles equal to each other.
Therefore,
ΔACB ~ ΔEFD
Hence,
AC / EF = CB / FD = AB / ED
Therefore, let's find x
x = AB
ED = 3.8
BC = 15
FD = 5
x / 3.8 = 15 / 5
cross multiply
5x = 15 × 3.8
5x = 57
divide both sides of the equation by 5
x = 57 / 5
x = 11.4
learn more on similar triangles here: https://brainly.com/question/17006564
#SPJ1
TRIGONOMETRY
Grade 10 Math
Calculate to the nearest 0.1 degree, the size of alpha in the drawing above.
Will give branliest and rate 5 stars for the best answer.
Need it urgently!!!
Thanks.

Answers
Check the picture below.
Make sure your calculator is in Degree mode.
\(\tan(\alpha )=\cfrac{\stackrel{opposite}{5}}{\underset{adjacent}{4}}\implies \alpha=\tan^{-1}\left( \cfrac{5}{4} \right)\implies \alpha \approx 51.3^o\)

helppppppppppppppppppppppppppppppppppppppppppp

Answers
Answer:
612 Children's dresses
Step-by-step explanation:
837 + 958 = 1795
2407 - 1795 = 612
3) show that the two lines with the given slopes are parallel, perpendicular neither. My₁ = 3/4 M₂ = 12/16 . solve it by showing step by step
Answers
Parallel lines have equal slope so
M1-M2=0Lets check
M1=3/4M2=12/16=3/4Now
M1-M23/4-3/40Lines are parallel
Answer:
The two lines are parallel
Step-by-step explanation:
If two lines are parallel, they have the same slope.
If two lines are perpendicular, the slopes will be negative reciprocals (the product of the slopes will be -1).
Given slopes:
\(\sf m_1=\dfrac{3}{4}\)
\(\sf m_2=\dfrac{12}{16}\)
Reduce m₂ to its simplest form by dividing the numerator and denominator by the largest common factor:
\(\sf m_2=\dfrac{12 \div 4}{16\div 4}=\dfrac{3}{4}\)
Therefore,
\(\sf as \quad \dfrac{3}{4}=\dfrac{3}{4} \implies m_1=m_2 \quad\)
As the given slopes are the same, the two lines are parallel.
Use the drawing tool(s) to form the correct answer on the provided number line. Will brought a 144-ounce cooler filled with water to soccer practice. He used 16 ounces from the cooler to fill his water bottle. He then took out 16 plastic cups for his teammates and put the same amount of water in each cup. Find and graph the number of ounces of water, x, that Will could have put in each cup.

Answers
According to the information, we can infer that the number of ounces of water, x, that Will could have put in each cup is 8 ounces.
What is the number of ounces of water "x" that Will could have put in each cup?Will initially had a cooler filled with 144 ounces of water. After using 16 ounces to fill his water bottle, there were 144 - 16 = 128 ounces of water remaining in the cooler.
Will then took out 16 plastic cups for his teammates. Since the same amount of water was put in each cup, the remaining amount of water, 128 ounces, needs to be divided equally among the cups.
Dividing 128 ounces by 16 cups gives us 8 ounces of water for each cup.
So, Will could have put 8 ounces of water in each cup.
Learn more about water in: https://brainly.com/question/28465561
#SPJ1

Without using a calculator, simplify the following expression to a single trigonometric term: 6.1 sin 10° cos 440 + tan(360°-0), sin 20 6.2 Given: sin(60° +2x) + sin(60° - 2x) 6.2.1 (3)
Answers
We are given two expressions to simplify. In the first expression, 6.1 sin 10° cos 440 + tan(360°-0), we need to simplify it to a single trigonometric term. In the second expression, sin(60° + 2x) + sin(60° - 2x), we are asked to evaluate it. By using trigonometric identities and properties, we can simplify and evaluate these expressions.
6.1 sin 10° cos 440 + tan(360°-0):
Using the trigonometric identity tan(θ + π) = tan(θ), we can rewrite tan(360° - 0) as tan(0) = 0. Therefore, the expression simplifies to 6.1 sin 10° cos 440 + 0 = 6.1 sin 10° cos 440.
sin(60° + 2x) + sin(60° - 2x):
Using the angle sum identity for sine, sin(a + b) = sin(a)cos(b) + cos(a)sin(b), we can rewrite the expression as sin(60°)cos(2x) + cos(60°)sin(2x). Since sin(60°) = √3/2 and cos(60°) = 1/2, the expression simplifies to (√3/2)cos(2x) + (1/2)sin(2x).
Note: The given expression sin(60° + 2x) + sin(60° - 2x) cannot be further simplified to a single trigonometric term. However, we can rewrite it in terms of cosine using the identity sin(x) = cos(90° - x), which results in (√3/2)cos(90° - 2x) + (1/2)cos(90° + 2x).
To learn more about trigonometric: - brainly.com/question/29156330#SPJ11
Please helppp please help

Answers
Answer:
a. parallel b. neither c. neither d. perpendicular
Step-by-step explanation:
Find the gradient of the line in the graph
Choose 2 coordinates, I choose (0,1) and (3,3)
Use the formula
(y2 - y1)/(x2 - x1)
(3 - 1) / (3 - 0)
2/3
Gradient of a parallel line is the same
Gradient of a perpendicular line formula m1m2 = -1
(2/3)m2 = -1
m2 = -3/2
The gradient of the perpendicular line will be -3/2
The gradient of the parallel line will be 2/3
Any other gradient will be neither parallel nor perpendicular.
What's the answer and how do you find the baring??

Answers
when getting a bearing, we're referring to the angle from the North line moving clockwise, so of D from C? well, the "from" point gets the North line and we check the angle from that North line clockwise to the other point, Check the picture below.

is the line through points p(-8,-10) and q(-5,-12) perpendicular to the line through points r(9,-6) and s(17,-5)
Answers
we dunno, hmmm let's check for the slope for PQ
\(P(\stackrel{x_1}{-8}~,~\stackrel{y_1}{-10})\qquad Q(\stackrel{x_2}{-5}~,~\stackrel{y_2}{-12}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-12}-\stackrel{y1}{(-10)}}}{\underset{\textit{\large run}} {\underset{x_2}{-5}-\underset{x_1}{(-8)}}} \implies \cfrac{-12 +10}{-5 +8} \implies \cfrac{ -2 }{ 3 } \implies - \cfrac{2 }{ 3 }\)
keeping in mind that perpendicular lines have negative reciprocal slopes, then if both are truly perpendicular, then line RS will have a slope of
\(\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{ \cfrac{-2}{3}} ~\hfill \stackrel{reciprocal}{\cfrac{3}{-2}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{3}{-2} \implies \cfrac{3}{ 2 }}}\)
let's see if that's true
\(R(\stackrel{x_1}{9}~,~\stackrel{y_1}{-6})\qquad S(\stackrel{x_2}{17}~,~\stackrel{y_2}{-5}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-5}-\stackrel{y1}{(-6)}}}{\underset{\textit{\large run}} {\underset{x_2}{17}-\underset{x_1}{9}}} \implies \cfrac{-5 +6}{8} \implies \cfrac{ 1 }{ 8 } ~~ \bigotimes ~~ \textit{not perpendicular}\)
Answer:
Step-by-step explanation:
No they are not perpendicular.
Perpendicular lines have slopes that are negative reciprocals of each other.
PQ slope = -12 - -10/-5 --8 = -2/3
RS slope = -5 - -6/17 -9 = 1/8
Slope are not negative reciprocals - the lines are not perpendicular.
Slope formula is m = y2 - y1/x2 - x1
Use this to determine slope.
For example if the the slope of RS was 3/2 - the lines would be perpendicular.
find the standard equation of the sphere with the given characteristics. center: (−1, −6, 3) radius: 5
Answers
The standard equation of the sphere with the given characteristics, center (-1, -6, 3), and radius 5 is
\((x+1)^{2} +(y+6)^{2}+ (z-3)^{2} =25\).
The standard equation of a sphere is \((x-h)^{2} +(y-k)^{2}+ (z-l)^{2} =r^{2}\), where (h, k, l) is the center of the sphere and r is the radius.
Using this formula and the given information, we can write the standard equation of the sphere:
\((x-(-1))^{2}+ (y-(-6))^{2} +(z-3)^{2}= 5^{2}\)
Simplifying, we get:
\((x+1)^{2} +(y+6)^{2}+ (z-3)^{2} =25\).
Therefore, the standard equation of the sphere with center (-1, -6, 3) and radius 5 is \((x+1)^{2} +(y+6)^{2}+ (z-3)^{2} =25\).
Learn more about the standard equation of the sphere here:
https://brainly.com/question/31706340
#SPJ11
4 cm
6 cm
8cm. Find the
Circumference of the
snowman

Answers
The number of degrees of freedom for the Student's t-test of a population mean is always 1 lessthan the (select)a. sample sizeb. significance levelc. sample meand. critical value
Answers
The number of degrees of freedom for the Student's t-test of a population mean is always 1 less than the sample size.
The correct answer is (a) sample size. In the context of the Student's t-test, the degrees of freedom represent the number of independent observations available to estimate the population parameter. For a one-sample t-test, the sample size determines the number of observations used to calculate the test statistic.
In the t-test, we compare the sample mean to a hypothesized population mean and assess whether any difference observed is statistically significant. The degrees of freedom in the t-test are calculated as n - 1, where n is the sample size. Subtracting 1 accounts for the loss of one degree of freedom due to estimating the sample mean. This adjustment is necessary because the sample mean is used to estimate the population mean.
By reducing the degrees of freedom by 1, the t-distribution becomes more concentrated around the mean, which affects the critical values and the calculation of p-values. This adjustment is specific to the t-distribution and is a key difference from the normal distribution, where degrees of freedom are not involved.
Learn more about subtracting here: https://brainly.com/question/13619104
#SPJ11
Please Help!
Which Triangles are similar and why?


Answers
Both because they are all the same triangle
A company prints T-shirts. They charge $40 plus $12 per shirt. So, the cost for n shirts is 40+ (12 x n). Choose
the answer that completes the table for this situation.

Answers
Answer:
Its the second table
Step-by-step explanation:
After solving a series of mathematical problems using a complicated formula, Mark uses the same formula to solve another problem he could have solved using a much simpler formula. Mark's continued reliance on the complicated formula BEST illustrates:
Answers
Answer:
C. mental set
Step-by-step explanation:
A mental set generally refers to the brain's tendency to stick with the most familiar solution to a problem and stubbornly ignore alternatives. This tendency is likely driven by previous knowledge (the long-term mental set) or is a temporary by-product of procedural learning (the short-term mental set).
Vani went to the store to buy some chicken. The price per pound of the
chicken is $3.50 per pound and she has a coupon for $3.25 off the final
amount. With the coupon, how much would Vani have to pay to buy 3 pounds
of chicken? Also, write an expression for the cost to buy p pounds of chicken,
assuming at least one pound is purchased.
PLEASE PROVIDE THE AMOUNT FOR P AND FOR 3 POUNDS
Answers
The cost is the cost per pound times the number of pounds minus the coupon.
If \(p\) pounds are purchased, she will pay \(3.50p-3.25\).
If 3 pounds are purchased, she will pay 3.50(3)-3.25=7.25.
The water's edge restaurant is currently running an offer of 15% of all food.
Chicken curry..........£6.20
Onion soup..............£4.00
Naan Bread..............£2.80
Mint Parfait................£3.80
Ice cream Delight....£2.60
How much do Dawn and Martin spend if they buy 2 chicken curries, 2 Onion soups, 1 Nann bread, 1 Mint parfait and 1 Ice cream delight?
£_____________
(If you don't know just tell me how to find 15% pls)

Answers
4x2=8
Add 2.80 to the above 20.40
23.20
Add 3.80 =27
Finally add 2.60 so total is 29.60
10% would be 2.96 - half of this is 1.48 (5%) so 15% would be 4.44
Answer:
1 . Chicken curries - £6.20 X 2 = £12.40 15% of £ 12.40 is £1.86 off = £10.54 +
2 .Onion Soups - £4.00 x 2 = £8.00 15% OF £8.00 is £ 1.20 off = £6.80
3. One Naan bread = £.2.80 15% of £ 2.80 is £ 0.42 p off = £2.38
4. One mint parfait = £ 3.80 15% of £ 3.80 is £ 0.57 p off = £ 3.23
5 .One ice cream delight = £2.60 15% of £ 2.60 is £0.39 p off £ 2.21
= £ 25.16
Step-by-step explanation:
1. to find out 15% from £12.40 you can divide 12.40 / 100 = 0.124 and then times 0.124 by the percentage = 0.124 x 15 = £ 1.86
2 . to find out 15% from £8.00 you divide again £8.00 / 100 =0.08 and then times 0.08 by the percentage 15 %= 0.08 x 15 = £1.20 off
3. £ 2.80 / 100 =0.028 x 15% = £0.42 p off
4. £ 3.80 /100 = 0.038 x 15% = £ 0.57 p off
5. £ 2.60 /100 = 0.026 x 15% = £ 0.39 p off
Hope that helped !
Here are two similar solid toys. The ratio of surface area of toys R: surface area of toy B is 7:9. The volume of toy B is 20cm^3. Work out the volume of toy A. Give your answer to 3 significant figures 

Answers
Answer:
13.7
Step-by-step explanation:
The computation of the volume of toy A is shown below:
7 × k^2=9
k^2= 9 ÷ 7
k=√9 ÷ 7
k = 1.133893419
Now
= 20 ÷ 1.133893419³
=13.7
Add and subtract the following fractions. Remember to find the LCD first.
1. 1/2 + 1/3
2. 1/6 + 1/8 + 1/3
3. 4/11 + 5/22 + 3/44
4. 3/4 - 3/8
5. 11/15 - 3/5
Answers
Answer:
1. 5/6
2. 5/8
3. 29/44
4. 3/8
5. -8/15
One cubic meter represents a cube shape that measures 1 meter in all three dimensions. how long is each side in centimeters?
Answers
Each side of cube is 100 cm.
What is a cube?In Maths or in Geometry, a Cube is a solid three-dimensional figure, which has 6 square faces, 8 vertices and 12 edges. It is also said to be a regular hexahedron.
Given that,
Volume of cube = 1 cubic meter
We know that,
1 m = 100 cm
Also volume of cube = \(a^{3}\)
Then,
Volume of cube = 1000000 cm
\(a^{3}\) = \(100^{3}\)
a = 100 cm
Hence, Each side of cube is 100 cm.
To learn more about cube from the given link:
https://brainly.com/question/1972490
#SPJ4
2 + 2 + 2 + 2 + 2 + 2 = 4 × ___
Answers
Answer:
2 + 2 + 2 + 2 + 2 + 2 = 4 × 3
Step-by-step explanation:
4x3=12
Those ones add up to 12
Hope this helps!
If f(x) = x³-6, find f(-4).
Answers
Answer:
-70
Step-by-step explanation:
f(x)=x^3 - 6
f(-4) = (-4)^3 - 6
f(-4) = -64 -6
f(-4) = -70
Evaluate the expression −x^2 + 2x-7 when X=-4
Answers
-(-4)^2+2(-4)-7
-16-8-7
=-31
The two main ways in which marketers address the competition with their strategies are by satisfying a need better than the competition and by _____. A. offering a lower price B. positioning the product C. segmenting the market D. entering new markets
Answers
The two main ways in which marketers address the competition with their strategies are by satisfying a need better than the competition and by positioning the product . The correct option is B
What is positioning ?Positioning is the process of forming a picture of the product in the target market's minds. To do this, a unique selling proposition (USP) must be developed that sets the product apart from the competition. A statement describing the advantages of the product and why it is superior to the competition is known as the USP.
Marketers use a variety of tools to position their products such as :
AdvertisingPublic relationsSales promotionTherefore, the correct answer is B. positioning the product.
Learn more about Positioning here : brainly.com/question/14976421
#SPJ1
Answer:
offering a lower price
Step-by-step explanation:
Need help pls help me on this question

Answers
Subtract 45 in both sides
Giving you 3x=27 divide by 3
X=9
Then do 72-45= 27
That’s your angle measure
Find and classify the critical points of f(x,y)=8r³+ y² + 6xy
Answers
The critical points of the function are (0, 0) and (3/4, -9/4), To classify the critical points, we need to examine the second partial derivatives of f(x, y) at each point
To find the critical points of the function f(x, y) = 8x^3 + y^2 + 6xy, we need to find the values of (x, y) where the partial derivatives with respect to x and y are equal to zero.
Taking the partial derivative with respect to x, we have:
∂f/∂x = 24x^2 + 6y = 0.
Taking the partial derivative with respect to y, we have:
∂f/∂y = 2y + 6x = 0.
Solving these two equations simultaneously, we get:
24x^2 + 6y = 0,
2y + 6x = 0.
From the second equation, we can solve for y in terms of x:
Y = -3x.
Substituting this into the first equation:
24x^2 + 6(-3x) = 0,
24x^2 – 18x = 0,
6x(4x – 3) = 0.
Therefore, we have two possibilities for x:
1. x = 0,
2. 4x – 3 = 0, which gives x = ¾.
Substituting these values back into y = -3x, we get the corresponding y-values:
1. x = 0 ⇒ y = 0,
2. x = ¾ ⇒ y = -9/4.
Hence, the critical points of the function are (0, 0) and (3/4, -9/4).
To classify the critical points, we need to examine the second partial derivatives of f(x, y) at each point. However, since the original function does not provide any information about the second partial derivatives, further analysis is required to classify the critical points.
Learn more about partial derivatives here:
https://brainly.com/question/32387059
#SPJ11
Given the linear functions f(x) = x − 2 and g(x) = −3x + 4, determine (f ⋅ g)(x).
Answers
In linear equation, The function we get (f.g)(x) =-3x+2
What is a linear equation?
A linear equation is a first-order (linear) term plus a constant in the algebraic form y=mx+b, where m is the slope and b is the y-intercept.
The variables in the preceding equation are y and x, and it is occasionally referred to as a "linear equation of two variables."
Given that,
The linear function are f(x)=x-2 and g(x)=-3x+4
= (f ⋅ g)(x).
= f(g(x))
= f(-3x+4)
= (-3x+4)-2
= -3x+4-2
= -3x+2
Therefore, The function we get (f.g)(x) =-3x+2
Learn more about linear equation
brainly.com/question/11897796
#SPJ1
Given the plant transfer function \[ G(s)=1 /(s+2)^{2} \] If using a PD-controller, \( D_{c}(s)=K(s+7) \), what value of \( K>0 \) will move both original poles back onto the real axis resulting in a
Answers
The value of K that moves both original poles back onto the real axis is 0. By setting K to zero, we eliminate the quadratic term and obtain a single pole at \( s = -2 \), which lies on the real axis.
The value of K that moves both original poles back onto the real axis can be found by setting the characteristic equation equal to zero and solving for K.
The transfer function of the plant is given by \( G(s) = \frac{1}{(s+2)^2} \). To move the original poles, we introduce a PD-controller with transfer function \( D_c(s) = K(s+7) \), where K is a positive constant.
The overall transfer function, including the controller, is obtained by multiplying the plant transfer function and the controller transfer function: \( G_c(s) = G(s) \cdot D_c(s) \).
To find the new poles, we set the characteristic equation of the closed-loop system equal to zero, which means we set the denominator of the transfer function \( G_c(s) \) equal to zero.
\[
(s+2)^2 \cdot K(s+7) = 0
\]
Expanding and rearranging the equation, we get:
\[
K(s^2 + 9s + 14) + 4s + 28 = 0
\]
To move the poles back onto the real axis, we need to make the quadratic term \( s^2 \) zero. This can be achieved by setting the coefficient K equal to zero:
\[
K = 0
\]
Learn more about quadratic here:
brainly.com/question/22364785
#SPJ11
if square one is the largest of the three squares in the model,which statement is true?
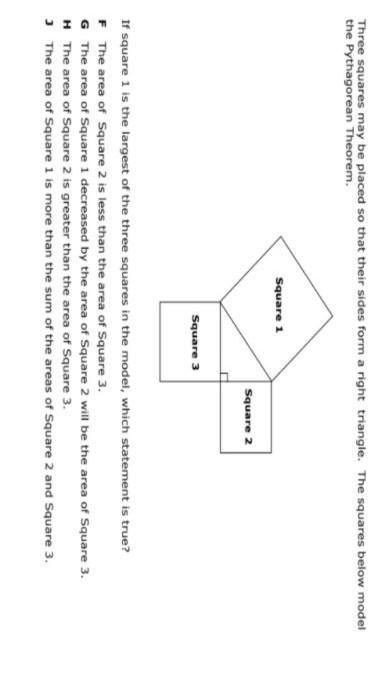
Answers
_______________
I'm reading your question
___________________
According to the Pythagorean theorem
Hypotenuse ^2 = Side 1 ^2 + Side 2 ^2
The hypotenuse is the case (Square 1 )
area of the sqaure= side of the square^2
________________________
That means the area of 1 is = area of square 2 + area fo square3 (J is false)
_______________________________
We are not sure about the relation between square 2 and 3 just the addition is the square 1 (F and H we have no certainty)
______________________________
G is true
______________________________
Answer
G
