Question 10 of 12
Nurse Sanders examines immunization records for this past winter at the
school where she works.
Got flu Didn't get flu Total
Vaccinated
14
586
600
Not vaccinated 20
130
150
Total
34
716
750
How many students were vaccinated but got the flu anyway?
A. 14
B. 20
C. 586
D. 600
SUBMIT
i’ll give brainlist<3

Answers
Answer:
14
Step-by-step explanation:
Because if you think then it say's it all
Give me brainlist <3 for dodge charger SRT Hellcat Redeye!!!!!!!!!
Answer:
14
Step-by-step explanation:
no trippie
Related Questions
let f (x) = x3 ln(1 x2), and let [infinity] Σ anx^n n=0be the taylor series of f about 0. thena3=a7=a12=
Answers
a₃ = a₇ = a₁₂ = 0. To find the values of a3, a7, and a12 in the Taylor series of f(x) = x^3 ln(1 - x^2) about 0, we need to determine the coefficients of the corresponding terms in the series expansion.
The general formula for the coefficients in the Taylor series expansion of a function f(x) about 0 is given by:
an = f⁽ⁿ⁾(0) / n!
where f⁽ⁿ⁾(0) represents the nth derivative of f evaluated at 0.
Let's calculate the derivatives of f(x) and evaluate them at 0 to find the coefficients.
f(x) = x^3 ln(1 - x^2)
f'(x) = 3x^2 ln(1 - x^2) + x^3 * (1 - x^2)^(-1)
f''(x) = 6x ln(1 - x^2) + 3x^2 * (1 - x^2)^(-1) - 6x^4 * (1 - x^2)^(-2)
f⁽³⁾(x) = 6 ln(1 - x^2) + 6x * (1 - x^2)^(-1) - 12x^3 * (1 - x^2)^(-2) + 24x^5 * (1 - x^2)^(-3)
Now, let's evaluate these derivatives at 0:
f(0) = 0
f'(0) = 0
f''(0) = 6
f⁽³⁾(0) = 6
The coefficients of the terms in the Taylor series expansion are determined by these derivatives. Specifically, the nth coefficient aₙ is equal to f⁽ⁿ⁾(0) / n!.
Therefore, we have:
a₃ = f⁽³⁾(0) / 3! = 6 / 6 = 1
a₇ = f⁽⁷⁾(0) / 7! = 0 / 5040 = 0
a₁₂ = f⁽¹²⁾(0) / 12! = 0 / 479,001,600 = 0
Hence, a₃ = a₇ = a₁₂ = 0.
Learn more about Taylor series here:
https://brainly.com/question/32235538
#SPJ11
It is a straight path that goes on without end in two directions. What is it?
A. line
B. plane
C.ray
D. triangle
Answers
The correct answer is A. line. A line is a straight path that extends infinitely in both directions. It has no endpoints and continues indefinitely.
A line is a basic geometric object that is defined by two points or can be represented by a single equation. It is characterized by its straightness and infinite length, extending in both directions without any boundaries or endpoints. A line can be represented by a straight line segment with two distinct points or by an equation such as y = mx + b in a coordinate system.
On the other hand, a plane refers to a two-dimensional flat surface that extends infinitely in all directions. It is not a straight path but rather a flat, continuous surface. A ray, is a part of a line that has one endpoint and extends infinitely in one direction. It is not a straight path that continues indefinitely in both directions like a line.
A triangle is a closed geometric shape with three sides and three angles. It is not a straight path but rather a closed figure formed by connecting three non-collinear points.Therefore ,the correct answer is A.
learn more about straight line :
https://brainly.com/question/31693341
#SPJ4
A ship travels a distance of 200 nautical miles in 10 1/2 hours. how many knots did the ship average each hour? (One knot equals 1 nautical mile per hour) Provide explination please
Answers
Answer:
19.05 knots average per hour
Step-by-step explanation:
Distance traveled = 200 nautical miles
Time taken = \(10\frac{1}{2}\) hours = \(\frac{10\times2+1}2=\frac{21}{2}\) hours
To find:
How many knots did the ship average each hour ?
Solution:
Here, we are given the distance traveled and total time taken to travel the distance.
As per question statement, we have to find the average speed of the ship.
Formula for average speed is given as:
\(\text{Average Speed = }\dfrac{\text{Total Distance traveled}}{\text{Total Time Taken}}\)
Putting the values in the formula:
\(\Rightarrow \text{Average Speed = }\dfrac{200}{\frac{21}{2}}\\\Rightarrow \text{Average Speed = }\dfrac{200\times 2}{21}\\\Rightarrow \text{Average Speed = }\dfrac{400}{21}\\\Rightarrow \text{\bold{Average Speed = 19.05 nautical miles per hour}}\)
It is also given that 1 nautical mile per hours is equal to one know.
Therefore, the average speed can be written as:
19.05 knots average per hour
When given a system 2 or more equations, the number of solutions to the system is
determined by...
Answers
Please help me, explain
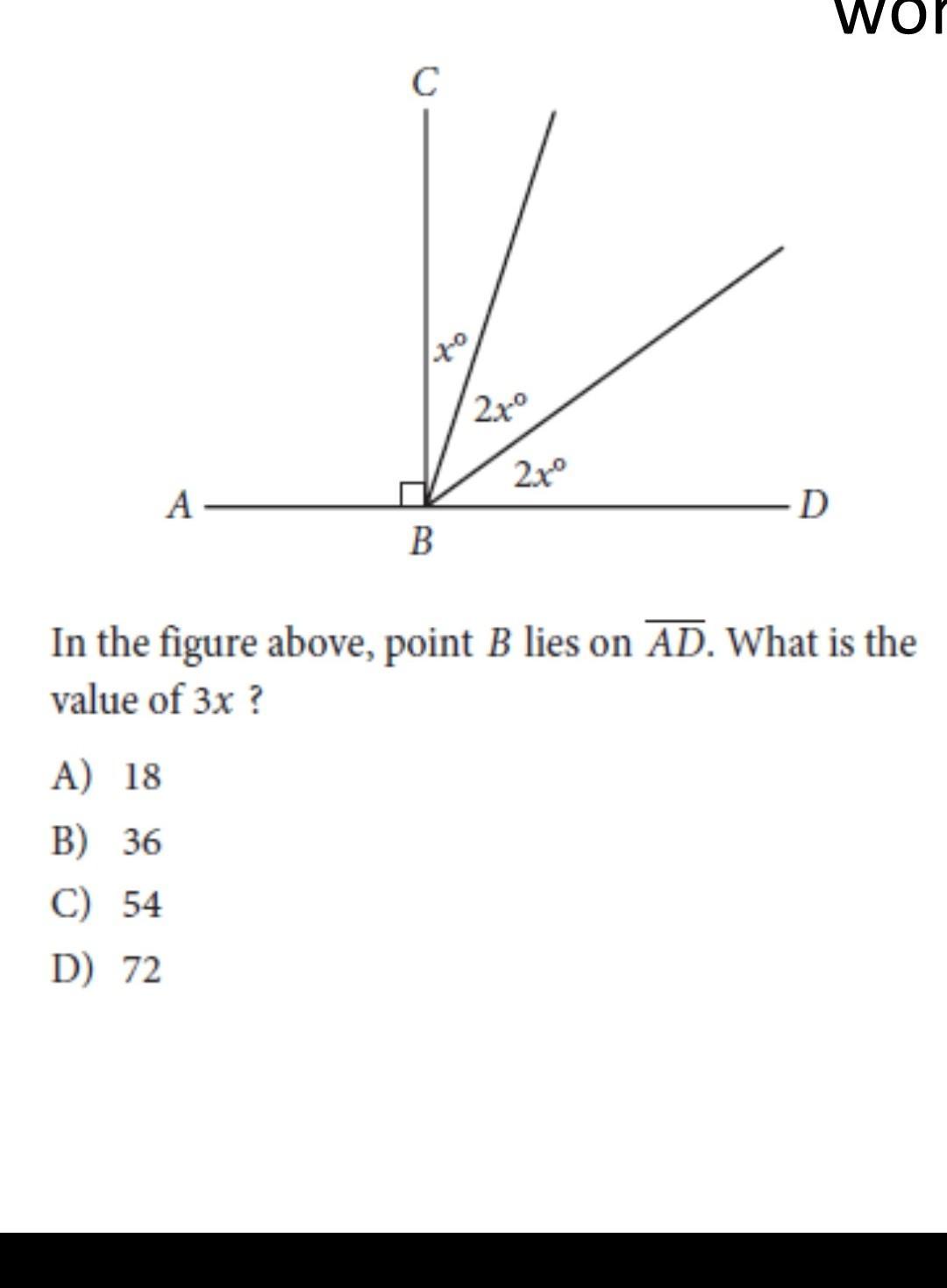
Answers
Answer:
C) 3x=54
Step-by-step explanation:
Angle ABD is a straight angle, which means it measures 180 degrees.
Angles ABC & CBD are linear pairs. (The two of them add up to 180°)
ABD is a right angle (90 degrees)
The straight angle (180) minus the right angle (90) equals 90 degrees.
x+2x+2x=90°
Combine like terms
5x=90°
divide by 5 on both sides
x=18
18×3=54
C
Hope this helps :-)
A pile of cards contains twelve cards, numbered 1 through 12. What is the probability of NOT choosing the 3?
Answers
11/12 is the probability of NOT choosing the 3.
Probability Definition in Math -
Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty. We can predict only the chance of an event to occur i.e. how likely they are to happen, using it.Four perspectives on probability are commonly used: Classical, Empirical, Subjective, and Axiomatic.There are 12 cards each having equals probability since all they appear once
Each card therefore has a probability of 1/12
Since there are 11 other numbers apart from 3
= 1/12 × 11
= 11/12
Learn more about probability
brainly.com/question/11234923
#SPJ4
The population
decreasing
of a country town is
at a rate of 4% p.a.
How many years will it take for the town's
population of 15000 to fall below 10000?
Answers
\(\qquad \textit{Amount for Exponential Decay} \\\\ A=P(1 - r)^t\qquad \begin{cases} A=\textit{current amount}\dotfill & \$10000\\ P=\textit{initial amount}\dotfill &15000\\ r=rate\to 4\%\to \frac{4}{100}\dotfill &0.04\\ t=years\\ \end{cases}\)
\(10000=15000(1 - 0.04)^{t} \implies \cfrac{10000}{15000}=(1 - 0.04)^{t}\implies \cfrac{2}{3}=0.96^t \\\\\\ \log\left( \cfrac{2}{3} \right)=\log(0.96^t)\implies \log\left( \cfrac{2}{3} \right)=t\log(0.96) \\\\\\ \cfrac{\log\left( \frac{2}{3} \right)}{\log(0.96)}=t\implies 9.93\approx t\qquad \textit{about 9 years and 11 months}\)
Be
1. (7.5A) Triangle ADE is similar to triangle ABG.
Which of the following statements must be true?
A. The measure of angle AGB is greater than the measure of angle ADE.
B. The measure of angle AGB is greater than the measure of angle AED.
C. Segment AE and Segment AB have the same length.
D. The ratio of AG to AE is the same as the ratio of AB to AD.

Answers
Answer:
D
Step-by-step explanation:
....iam not sure but i think its a because the other impossible
Answer:
The answer is D.
Step-by-step explanation:
For A- I don't think it's greater, I think they are the same.
For B- I don't think it's greater, I think they are the same.
For C- Segment AE is longer than Segment AB.
So D seems like the more logical answer.
every polynomial function of odd degree with real coefficients will have at least
Answers
Every polynomial function of odd degree with real coefficients will have at least one real root or zero.
This statement is known as the Fundamental Theorem of Algebra. It states that a polynomial of degree n, where n is a positive odd integer, will have at least one real root or zero.
The reason behind this is that when a polynomial of odd degree is graphed, it exhibits behavior where the graph crosses the x-axis at least once. This implies the existence of at least one real root.
For example, a polynomial function of degree 3 (cubic polynomial) with real coefficients will always have at least one real root. Similarly, a polynomial function of degree 5 (quintic polynomial) with real coefficients will also have at least one real root.
It's important to note that while a polynomial of odd degree is guaranteed to have at least one real root, it may also have additional complex roots.
The Fundamental Theorem of Algebra ensures the existence of at least one real root but does not specify the total number of roots.
In summary, every polynomial function of odd degree with real coefficients will have at least one real root or zero, as guaranteed by the Fundamental Theorem of Algebra.
To know more about polynomial function refer here:
https://brainly.com/question/29054660#
#SPJ11
What is the probability that a randomly selected value from the distribution will be less than 2.1 standard deviation from the mean
Answers
Answer:
0.9821
Step-by-step explanation:
Probability that a randomly selected value will be less than 2.1 deviations from the mean ; this means the Zscore = 2.1
Hence, using :
P(Z < 2.1) = 0.9821 (standard normal table
= 0.9821
Identify the center and shape of the distribution:
Center =
Shape =

Answers
The center and shape of the distribution are respectively:
9.6
Skewed left
What is the center and shape of the distribution?The center of a distribution is a found using a statistics such as mean, median, or mode, and then provides a single value that is representative of the data. The spread is one that describes how close the data values are to each other using the range or standard deviation. The shape is one that describes how the data looks on a graph.
From the bar graph, we see that the center of the distribution is at 9.6.
Similarly, we also see that it is skewed left because it is longer on the left side of its peak than on its right.
Read more about Shape of the distribution at: https://brainly.com/question/29459693
#SPJ1
1. What is m
A 51
B 129
C 134
D 141
Answers
you note that your prescription for new eyeglasses is −4.95 d. what will their focal length (in cm) be?
Answers
The focal length of the lenses needed for vision correction is approximately -20.20 cm, which means they are concave lenses (used for myopia).
As per the question given,
The prescription for a new pair of glasses is given in dioptres, a unit of measure used to describe the refractive power of a pair of glasses. In this case, a prescription of -4.95 D means that the lenses required for vision correction have a refractive power of -4.95 dioptres.
To determine the focal length of your lenses in centimetres, you can use the following formula:
focal length (cm) = 100 / refractive power (diopters)
Using Recipes -4.95D as an example, the focal length can be calculated as follows:
focal length (cm) = 100 / -4.95 D = -20.20 cm
It is important to note that a negative sign on your prescription indicates that you are nearsighted.
For such more questions on Focal length
https://brainly.com/question/9074547
#SPJ4
What is the value of \(\frac{81^4}{3^5}\)? (Express your answer in exponential form.)
Answers
Answer:\(3^1^1\\\)
Step-by-step explanation:
\(\frac{81^4}{3^5}\)
\(\frac{3^1^6}{3^5}\)
The base is same power can be add or subtract
\(3^1^6^-^5\)
\(3^1^1\)
I need help!! I can’t do this!

Answers
Answer:
S +2J = 48S -J = 3Step-by-step explanation:
You want a system of equations that represents the relations between Sally's age and Jerry's age.
First stepThe first step in dealing with a word problem is to engage your brain. There can be a tendency to start by saying "I can't do this!", which will turn off your brain and guarantee that you will have trouble. If you realize the words have their usual English meaning, then understanding what they are saying is not so hard.
Second stepOnce you have read the question and identified what it is asking for (equations for ages), then you can figure out what to do. Usually, you will want to assign tokens (variables) for the things that are being asked for (ages).
It is often convenient to choose variables that remind you what they stand for. Here, it is convenient to use S for Sally's age, and J for Jerry's age. Your answer to the question will be equations that relate S and J.
Third stepNow you can get into the details of the relationships that are being described.
A sum is the addition of two or more items. Here the items are (Sally's age) and (twice Jerry's age). Twice means "two times," so "twice Jerry's age" will be represented by 2×J, or simply 2J. That sum is ...
S + 2J . . . . . . "sum of Sally's age plus twice Jerry's age"
The problem tells us this is 48, so the first equation is ...
S + 2J = 48
The wording of the second sentence tells you how to write the second equation:
Sally's age minus Jerry's age is 3
S - J = 3
SummaryThe system of equations you're looking for is ...
S +2J = 48S -J = 3__
Additional comment
In general, if you want to obtain a solution, you will need as many equations as there are variables. Here, the problem statement gives two relations in two sentences. Those relations give two equations in the two variables. This is the "system of equations" that is being asked for.
Assume the base unit of water is 555 gallons and the cost per unit is $1.74. How much money will be saved in a month by a family who conserves 8000 gallons of water per month?
Answers
1) Gathering the data
555 gallons ----- $ 1.74
2) If 8000 gallons could be spent
If a Family conserves 8000 gallons this family would not have an expense of?
Let's set a proportion for that:
555 g-----$1.74
8000g ---x
555x =13920 Dividing both sides by 555
x=25.08
If a family conserves 8000 gallons of water. They save $25.08 per month assuming that $1.74 is equal to 555 gallons of water.
In terms of c, y, and a , what is the value of x in the equation
2ax + 2y = c?

Answers
Answer:
Step-by-step explanation:
Simplifying
2ax + 2y = c
Solving
2ax + 2y = c
Solving for variable 'a'.
Move all terms containing a to the left, all other terms to the right.
Add '-2y' to each side of the equation.
2ax + 2y + -2y = c + -2y
Combine like terms: 2y + -2y = 0
2ax + 0 = c + -2y
2ax = c + -2y
Divide each side by '2x'.
a = 0.5cx-1 + -1x-1y
Simplifying
a = 0.5cx-1 + -1x-1y
The value of the equation in terms of c, y, and a is (x - 2y)/2a so option (D) will be correct.
What is the equation?There are many different ways to define an equation. The definition of an equation in algebra is a mathematical statement that demonstrates the equality of 2 mathematical expressions.
More than one variable may be present inside a linear equation. An equation is said to be linear if the maximum power of the variable is consistently unity.
In another word, the equation must be constrained with some constraints.
Given the equation,
2ax + 2y = c where x and y are variable and c is constant.
Now,
2ax + 2y = c
2ax = x - 2y
Divide by 2a into both sides
x = (x - 2y)/2a
Hence "The value of the equation in terms of c, y, and a is (x - 2y)/2a".
For more about the equation,
brainly.com/question/10413253
#SPJ2
An adiabatic process is one in which the:
-temperature remains constant.
-pressure on the air parcel remains constant.
-altitude of the air parcel remains constant.
-work done is zero.
-heat exchanged with the surroundings is zero.
Answers
An adiabatic process is one in which the heat transered between a system and its surroundings is equal to zero( q = 0 ). So, option(e) right one.
In thermodynamics, the adiabatic process is a process in which there is no heat or air exchange between the temperature and the environment. It is different from the isothermal heat flow process. Some important properties are :
In case of adiabatic compression (Q=0) of gas, work is done on it and its temperature increases. In case of adiabatic expansion of gas work done by it and its temperature decreases. That is temperature not constant. Pressure does not remain constant during an adiabatic process and it changes along with Volume.There is a thermodynamic change but no heat is exchanged between a system and its surroundings.Hence, option(e) is right answer.
For more information about heat transfer, refer:
https://brainly.com/question/31053699
#SPJ4
A 90% confidence interval for Mi - H2 is (-4.3. -1.9). Interpret the interval. O With 90 % confidence, the mean time on the test for non-schizophrenics is between 1.9 and 4.3 minutes more than the mean time for schizophrenics. O At the 90% level of confidence, there is not sufficient evidence to conclude that the mean time on the test for non-schizophrenics differs from the mean time for schizophrenics. O With 90 % confidence, the mean time on the test for non-schizophrenics is between 1.9 and 4.3 minutes less than the mean time for schizophrenics.
Answers
The correct interpretation of the given 90% confidence interval (-4.3, -1.9) is: "With 90% confidence, the mean time on the test for non-schizophrenics is between 1.9 and 4.3 minutes less than the mean time for schizophrenics."
Here's how we arrive at this interpretation: A confidence interval is a range of values within which we estimate the true population parameter to lie with a certain level of confidence. In this case, the parameter of interest is the difference between the means of two populations: Mi (mean time for non-schizophrenics) and H2 (mean time for schizophrenics). The confidence interval (-4.3, -1.9) provides an estimate for this difference. The lower bound of -4.3 suggests that, with 90% confidence, the true mean difference between the two populations is at least -4.3 minutes. Similarly, the upper bound of -1.9 suggests that the true mean difference is at most -1.9 minutes.
Since the interval spans negative values, we can conclude that, on average, non-schizophrenics tend to take less time on the test compared to schizophrenics. The magnitude of the difference is estimated to be between 1.9 and 4.3 minutes, with 90% confidence. It's important to note that the interpretation states "between 1.9 and 4.3 minutes less," indicating that the mean time for non-schizophrenics is lower than the mean time for schizophrenics. This is consistent with the negative values of the confidence interval. Therefore, the correct interpretation is that, with 90% confidence, the mean time on the test for non-schizophrenics is estimated to be between 1.9 and 4.3 minutes less than the mean time for schizophrenics.
Learn more about interval here: brainly.com/question/32248724
#SPJ11
Citrus County's assets have an average duration of 8 and a market value of $1 million. The market interest rate is 5%. Use the duration formula to estimate the market value if the interest rate changes to 4%. 1,055,284 1,097.331
Answers
The estimated market value of Citrus County's assets, with an average duration of 8 and a market value of $1 million, would be approximately $1,055,284 if the interest rate changes to 4%.
In this case, the assets have an average duration of 8. When the interest rate changes from 5% to 4%, the change in interest rates is 1%. By applying the duration formula, the estimated percentage change in the market value of the assets would be approximately -8% (negative duration multiplied by the change in interest rates).
To calculate the estimated market value, we need to multiply the estimated percentage change (-8%) by the current market value ($1 million) and add it to the current market value. Thus, the estimated market value would be approximately $1,055,284 (1,000,000 + (1,000,000 * -8%)).
Duration is a measure of the sensitivity of an asset's price to changes in interest rates. It provides an estimate of the percentage change in the market value of an asset for a given change in interest rates. The duration formula states that the percentage change in the market value of an asset is approximately equal to the negative duration multiplied by the change in interest rates.
to learn more about market value click here:
brainly.com/question/28320555
#SPJ11
Which of the following are solutions to the inequality 5 < X ?
Answers
The inequality:
\(\begin{gathered} 55 \end{gathered}\)Basically tells us that the solutions will be the numbers strictly greater than 5, so:
\(\begin{gathered} 3>5 \\ False \\ ---- \\ 8>5 \\ True \\ ---- \\ 10>5 \\ True \\ ---- \\ 6>5 \\ True \end{gathered}\)Therefore, the solutions are:
8, 10, 6
A security car is parked 25 ft from a movie theater. Find at what speed the reflection of the security strobe lights is moving along the wall of the movie theater when the reflection is 30 ft from the car. The strobe lights are rotating with the speed 2 revolutions per second.
Answers
Answer:
v=20π ft/s
Step-by-step explanation:
Given:
Distance from the security car to the movie theater, D=25 ft
Distance of the reflection from the car, d=30 ft
Speed of rotation of the strobe lights, 2 rev/s
To find the speed at which the reflection of the security strobe lights is moving along the wall of the movie theater, we need to calculate the linear velocity of the reflection when it is 30 ft from the car.
We can start by finding the angular velocity in radians per second. Since the strobe lights rotate at 2 revolutions per second, we can convert this to radians per second.
ω=2πf
=> ω=2π(2)
=> ω=4π rad/s
The distance between the security car and the reflection on the wall of the theater is...
r=30-25= 5 ft
The speed of reflection is given as (this is the linear velocity)...
v=ωr
Plug our know values into the equation.
v=ωr
=> v=(4π)(5)
∴ v=20π ft/s
Thus, the problem is solved.
The speed of the reflection of the security strobe lights along the wall of the movie theater is 2π ft/s.
To solve this problem, we can use the concept of related rates. Let's consider the following variables:
x: Distance between the security car and the movie theater wall
y: Distance between the reflection of the security strobe lights and the security car
θ: Angle between the line connecting the security car and the movie theater wall and the line connecting the security car and the reflection of the strobe lights
We are given:
x = 25 ft (constant)
y = 30 ft (changing)
θ = 2 revolutions per second (constant)
We need to find the speed at which the reflection of the security strobe lights is moving along the wall (dy/dt) when the reflection is 30 ft from the car.
Since we have a right triangle formed by the security car, the movie theater wall, and the reflection of the strobe lights, we can use the Pythagorean theorem:
x^2 + y^2 = z^2
Differentiating both sides of the equation with respect to time (t), we get:
2x(dx/dt) + 2y(dy/dt) = 2z(dz/dt)
Since x is constant, dx/dt = 0. Also, dz/dt is the rate at which the angle θ is changing, which is given as 2 revolutions per second.
Plugging in the known values, we have:
2(25)(0) + 2(30)(dy/dt) = 2(30)(2π)
Simplifying the equation, we find:
60(dy/dt) = 120π
Dividing both sides by 60, we get:
dy/dt = 2π ft/s
For more such question on speed. visit :
https://brainly.com/question/26046491
#SPJ8
You wanted to make the perfect banana split sundae. There are 9 items that you need and
they are locked away. In order to unlock these items, you must complete 9 tasks. The locks
could contain numbers, letters, or both. Unlocking a task will enable you to add an item to
your banana split. In order to complete the perfect banana split sundae, you must complete
all 9 tasks correctly and unlock all 9 missing items.
Answers
Answer:
25
Step-by-step explanation:
math
How do I do this? I’m lost

Answers
Answer:
x=12
Step-by-step explanation:
3x+7=5x-17
2x=24
x=12
Prove that sin2theta sin4theta sin6theta by cos2theta cos4theta cos6theta=tan4theta
Answers
Sin2x sin4x sin6x/cos2x cos4x cos6x = tan4x.
What is trigonometric functions?Trigonometric functions are functions that relate the angles of a triangle to the lengths of its sides. They are commonly used in mathematics to solve problems involving angles, distances, and height. The most commonly used trigonometric functions are sine, cosine, and tangent.
Let theta=x. Then, sin2x sin4x sin6x/cos2x cos4x cos6x= tan4x.
Using the identities of trigonometric functions, we can expand the left hand side of the equation as:
(sin2x)(sin2x×sin2x) (sin2x×sin2x*sin2x) / (cos2x)(cos2x×cos2x) (cos2x×cos2x×cos2x)
= (sin2x)((1-cos2x)×(1-cos2x)) ((1-cos2x)×(1-cos2x)×(1-cos2x)) / (cos2x)((1+cos2x)×(1+cos2x)) ((1+cos2x)×(1+cos2x)×(1+cos2x))
= (sin2x)(1-2cos2x+cos4x) (1-3cos2x+3cos4x-cos6x) / (cos2x)(1+2cos2x+cos4x) (1+3cos2x+3cos4x+cos6x)
By simplifying the equation, we get:
= (sin2x)(1-2cos2x+cos4x)(1-3cos2x+3cos4x-cos6x) / (cos2x)(1+2cos2x+cos4x)(1+3cos2x+3cos4x+cos6x)=
=sin2x (1-2cos2x+cos4x) / (cos2x)(1+2cos2x+cos4x)
= sin2x / cos2x - 2sin2x / (cos2x)(1+2cos2x+cos4x)
= tan2x - 2tan2x / (1+2cos2x+cos4x)
= tan2x (1 - 2 / (1+2cos2x+cos4x))
= tan2x (1+2cos2x+cos4x - 2) / (1+2cos2x+cos4x)
= tan2x (2cos2x + cos4x - 2) / (1+2cos2x+cos4x)
= tan2x (2cos2x + cos4x - 2) / (1+2cos2x+cos4x)
= tan4x
Therefore, sin2x sin4x sin6x/cos2x cos4x cos6x = tan4x.
To know more about trigonometric functions click-
https://brainly.com/question/25618616
#SPJ4
Use the expression
set of parentheses
32 divided by10-8 divided by 2-3 to create an expression that includes a
so that the value of the expression is 5.

Answers
Answer:(10-8)
Step-by-step explanation:
10-8=2
32/2 =16
16/2= 8
8-3=5
32/ (10-8) /2-3
v v
32/2 /2-3
v v
16/2 -3
v v
8-3
v
5
a card is chosen at random from a standard deck of cards, and then a letter is chosen from the word incredible
Answers
Answer: hope this helps
Step-by-step explanation:
There is a 4/52 chance of getting a king, because there are 52 cards in a deck, and 4 kings in each. And there is a 2/10 (1/5) chance of getting an i, because there are 2 i's in the word "incredible", and 10 letters (so simplifying that, you would get 1/5).
Solve y3 = −8. Please help im desperate
Answers
Answer:
-2
Step-by-step explanation:
y^3=-8.
y=cube root of -8 = -2
please help me with this real quick.

Answers
Help me out please?!
