Answers
Answer:
100,000,000,000,000,000
Related Questions
Christopher's boat travels 45 miles downstream in 3 hours. The return trip upstream takes 5
hours. Find the speed of the boat in still water and the speed of the current.
Ibistancolo
Answers
To solve this problem, we'll use the formula:
speed = distance/time
Let's start with the downstream trip. We know that Christopher traveled 45 miles in 3 hours. So:
speed downstream = 45 miles / 3 hours
speed downstream = 15 miles per hour
Now let's move on to the upstream trip. We know that this trip took 5 hours, but we don't know the distance yet. However, we do know that Christopher's boat travels at a certain speed in still water (let's call that speed "x") and that there is a current that slows him down when he's going upstream (let's call the speed of the current "y"). So:
distance upstream = (x - y) * 5
Now we can use the formula again to find the speed upstream:
speed upstream = distance upstream / time upstream
speed upstream = (x - y) * 5 / 5
speed upstream = x - y
We also know that the speed downstream is 15 mph faster than the speed upstream (since the current is helping Christopher along when he's going downstream). So:
speed downstream = speed upstream + 15
15 mph = x - y + 15
x - y = 0
Now we have two equations:
x + y = 15
x - y = 0
We can solve for x (the speed of the boat in still water) by adding these two equations together:
2x = 15
x = 7.5 mph
Now we can plug x back into one of the equations to solve for y (the speed of the current):
7.5 + y = 15
y = 7.5 mph
So the speed of the boat in still water is 7.5 mph and the speed of the current is 7.5 mph.
Let's use the following variables:
- B = speed of the boat in still water
- C = speed of the current
During Christopher's downstream trip, the boat's effective speed is the sum of the boat's speed in still water and the speed of the current (B + C). We can use the formula distance = time × speed to find the effective speed:
45 miles = 3 hours × (B + C) => (B + C) = 45 miles / 3 hours = 15 mph
For the upstream return trip, the effective speed is the difference between the boat's speed in still water and the speed of the current (B-C):
45 miles = 5 hours × (B - C) => (B - C) = 45 miles / 5 hours = 9 mph
Now we have two equations:
1) B + C = 15
2) B - C = 9
We can solve this system of equations by adding the two equations together:
(1) + (2): 2B = 24 => B = 12 mph
Now that we have the speed of the boat in still water, we can find the speed of the current by plugging B into either equation (1) or (2). We'll use equation (1):
B + C = 15 => 12 + C = 15 => C = 3 mph
So, the speed of the boat in still water is 12 mph, and the speed of the current is 3 mph.
Learn more about speed here:- brainly.com/question/17661499
#SPJ11
someone please help me

Answers
Answer:
Option B (2 in the blank)Step-by-step explanation:
Given function:
f(x) = 2x² - 5x + 7The leading term is 2x², the leading coefficient is 2, this is positive.
The graph opens upward.
Correct option is B.
False, because 2 > 0Option B is correct trust me my guy
the standard deviation is a resistant measure of spread. t/f
Answers
True, the standard deviation is a resistant measure of spread.
The standard deviation is calculated as the square root of the variance of the data set. Variance is calculated as the average of the squared differences between each data point and the mean of the data set. The standard deviation is the square root of this average.
In mathematical terms, the standard deviation can be calculated using the following formula:
σ = √(1/n ∑(x - μ)²)
Where σ is the standard deviation, n is the number of data points in the data set, x is the value of the i-th data point, and μ is the mean of the data set.
The standard deviation is an important measure because it gives an idea of how much the individual values in a data set differ from the mean.
In summary, the standard deviation is a resistant measure of spread because it gives a robust measure of the spread of the data in a set and is not easily influenced by outliers or extreme values.
To know more about standard deviation here.
https://brainly.com/question/16555520
#SPJ4
Given <2 and <4 are vertical angles. Prove <2
<4

Answers
Angle 2 and angle 4 are congruent.
What are vertical angles?
When two lines cross at a point, vertical angles are created. They are always on an equal footing. In other words, four angles are created anytime two lines cross or intersect. It is evident that two opposed angles are equal and are referred to as vertical angles.
Given,
∠2 and ∠4 are vertical angles as shown in fig.
We know that Vertical angles are formed when two straight lines intersect at a point. Vertical angles are two angles that are vertically opposite and have the same measure. So, the two angles are to be congruent.
We have to prove that angles 2 and angle 4 are congruent.
Given ∠2 and ∠3 makes linear pair so,
∠2 + ∠3 = 180
∠3 = 180 - ∠2....(1)
Again, ∠3 and ∠4 make linear pair
∠3 + ∠4 = 180
∠3 = 180 - ∠4....(2)
From (1) and (2) we get,
180 - ∠2 = 180 - ∠4
Subtracting 180 from both sides we get,
- ∠2 = - ∠4
∠2 = ∠4
Hence, angle 2 and angle 4 are congruent.
To learn more about the vertical angles from the given link
https://brainly.com/question/18450499
#SPJ1
The equation of the line passing through the point (2,3) with slope 2
Answers
Answer:
I have no rights to the answer
Original answer was created by
vivek8740
Step-by-step explanation:
https://brainly.in/question/31418586

Which ratio is equivalent to 12/2

Answers
Answer:
36/6
Step-by-step explanation:
12 x 3= 36.
2 x 3= 6.
Answer:
C. \(\frac{36}{6}\)
Step-by-step explanation:
1. What is −12 + |−3| − |−14|?
2. The depth of a local river averages 25 ft, which is represented as |−25|. In January, it measured 5 ft deep, or |−5|, and in July, it was 27 ft, or |−27|. What is the difference between depths in January and July?
3. What is the value of −3 + |−17|?
Answers
Answer:
1. -1 2. -22 i think may be wrong 3. -20
Step-by-step explanation:
good ol integers payin off
a family originally bought a home for $273,830. Now the home’s value is 30% higher than that. What is the value of the home now?
Answers
$355,394
100% +30% = 130% = 1.3
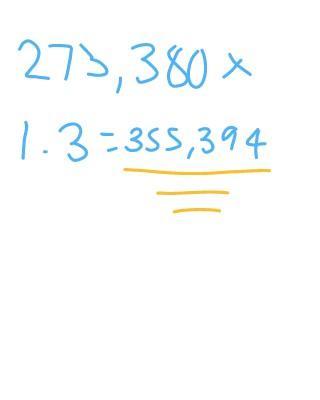
Answer:
So the home value is 30 percent higher then the original price.
So $273,830
It’s 30 percent higher.
I’m gonna do a short cut here but you can always find 30 percent of the number and add it back to the original value.
Well first 30 percent is 30/100 really since percent is out of a hundred.
We’re increasing 30 percent of the value.
The original value is already 100/100 since thats the full price and original.
We’re adding 30 percent of that so the new value is 130/100 or 130%
This would save a lot of steps and it’s a better way.
So find percentage like what we would do with any other equation.
Since here it’s 130% we multiply the value by 1.3.
Since 130/100 is 1.3 or you can always move the decimal to the left by 2 since it’s divided by a 100.
Now we multiply.
$273,830 * 1.3 = $355,979
Final answer is $355,979
The measures of the angles of a triangle are shown in the figure below. Solve for x.

Answers
x=180°-(102°+43°)=180°-145°=35°
how do u do number 10?

Answers
Answer:
C is the correct option
to test whether the overall regression equation is statistically significant one uses a. the r2-statistic. b. the standard error statistic. c. the f-statistic. d. the t-statistic.
Answers
One can use the f-statistic to test whether the overall regression equation is statistically significant, one uses the f-statistic.
A reasonably high R-squared score makes sense if your regression model includes independent variables that are statistically significant. According to the statistical significance, shifts in the dependent variable are correlated with changes in the independent variables.
The ratio of two variances is known as an F-statistic, and it bears Sir Ronald Fisher's name. Variances gauge how widely apart the data points are from the mean. When the individual data points tend to deviate further from the mean, there are more variances.
The F-test determines that it is unlikely that all of the coefficients will equal zero by adding the predictive power of all independent variables. But it's likely that none of the variables are individually important enough to be statistically significant.
Learn more about f-statistic at
https://brainly.com/question/18403256?referrer=searchResults
#SPJ4
3x-6= 5x - 2
Based on the equation above, what is the value of
2x-4?
A) -8
B) -2
C) 2
D) 6
Answers
The value of the expression is -8. Option A
How to determine the value
It is important to note that algebraic expressions are expressions that are made up of variables, terms, coefficients, constant and factors.
From the information given, we have that;
3x-6= 5x - 2
collect like terms
3x - 5x = -2 +6
subtract the like terms
-2x = 4
Make 'x' subject
x = -2
Substitute the value in the equation
2x - 4
2(-2) - 4
expand bracket
-8
Hence, the value is -8
Learn about algebraic expressions at: https://brainly.com/question/4344214
#SPJ1
Determine the frequency of each class in the table shown. Number of Candles in a Glass Jar Class Frequency 1003 1062 1063 1122 1123 1182 1183 1242 1243 1302 1303 1362
Answers
The frequency of a class is the number of data points that fall within the class is 1.
To determine the frequency of each class in the table shown, we must first divide the data points into the respective classes. The classes are 1003, 1062, 1063, 1122, 1123, 1182, 1183, 1242, 1243, 1302, 1303, and 1362.
For the class 1003, the frequency is 1, since there is only one data point (1003) in this class.
For the class 1062, the frequency is also 1 since there is only one data point (1062) in this class.
For the class 1063, the frequency is also 1 since there is only one data point (1063) in this class.
For the class 1122, the frequency is 1 since there is only one data point (1122) in this class.
For the class 1123, the frequency is 1 since there is only one data point (1123) in this class.
For the class 1182, the frequency is 1 since there is only one data point (1182) in this class.
For the class 1183, the frequency is 1 since there is only one data point (1183) in this class.
For the class 1242, the frequency is 1 since there is only one data point (1242) in this class.
For the class 1243, the frequency is 1 since there is only one data point (1243) in this class.
For the class 1302, the frequency is 1 since there is only one data point (1302) in this class.
For the class 1303, the frequency is 1 since there is only one data point (1303) in this class.
For the class 1362, the frequency is 1 since there is only one data point (1362) in this class.
Therefore, the frequency of each class in the table shown is 1.
Learn more about frequency here :
https://brainly.com/question/5102661
#SPJ4
WILL GIVE BRAINLIEST

Answers
Answer:
A
Step-by-step explanation:
JK is longer than JL and isn't 9 units long
What is the sign of c÷d when c >0 and d < 0.
Plzzz helppp im in class right now
Answers
Answer:
Negative
Step-by-step explanation:
Assume that you mean if c÷d is positive or negative when c > 0 and d < 0
c > 0 means that c is positive
d < 0 means that d is negative
positive divides negative is always negative.
Thus, c÷d is negative when c > 0 and d < 0
Write the expression:
"twelve less than two times a number"
Answers
Answer:
12-2x
Step-by-step explanation:
less than two times a number means 2x here is another example twenty-four times a number 24x
Answer:
12-2x
Step-by-step explanation:
Hope this helps :3
if Vector a = (2, 2k), Vector b = (4, -k), are perpendicular, solve for k
Answers
The value of k that makes vectors a and b perpendicular is k = 2. Since vectors a and b are given as (2, 2k) and (4, -k) respectively, the value of k that makes them perpendicular is k = 2
Two vectors are perpendicular if their dot product is equal to zero. To determine the value of k that makes vectors a and b perpendicular, we can calculate their dot product and set it equal to zero.
The dot product of vectors a and b is given by:
a · b = (2)(4) + (2k)(-k) = 8 - 2k²
Setting the dot product equal to zero, we have:
8 - 2k² = 0
Simplifying the equation, we get:
2k² = 8
Dividing both sides of the equation by 2, we have:
k² = 4
Taking the square root of both sides, we obtain:
k = ±2
Since vectors a and b are given as (2, 2k) and (4, -k) respectively, the value of k that makes them perpendicular is k = 2.
Learn more about vectors here:
https://brainly.com/question/24256726
#SPJ11
∂²p/∂r² + 1/r ∂p/∂r = ϕμC/k ∂p/∂t
derivation of equations
1-partial derivative diffusivity equation spherical flow
2- partial derivative diffusivity equation hemi- spherical flow
Answers
The partial derivative diffusivity equation for spherical flow is ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t, and for hemispherical flow, it is the same equation.
1. The partial derivative diffusivity equation for spherical flow is derived from the spherical coordinate system and applies to radial flow in a spherical geometry. It can be expressed as ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t.
2. The partial derivative diffusivity equation for hemispherical flow is derived from the hemispherical coordinate system and applies to radial flow in a hemispherical geometry. It can be expressed as ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t.
1. For the derivation of the partial derivative diffusivity equation for spherical flow, we consider a spherical coordinate system with the radial direction (r), the azimuthal angle (θ), and the polar angle (φ). By assuming steady-state flow and neglecting the other coordinate directions, we focus on radial flow. Applying the Laplace operator (∇²) in spherical coordinates, we obtain ∇²p = (1/r²) (∂/∂r) (r² ∂p/∂r). Simplifying this expression, we arrive at ∂²p/∂r² + (1/r) ∂p/∂r.
2. Similarly, for the derivation of the partial derivative diffusivity equation for hemispherical flow, we consider a hemispherical coordinate system with the radial direction (r), the azimuthal angle (θ), and the elevation angle (ε). Again, assuming steady-state flow and neglecting the other coordinate directions, we focus on radial flow. Applying the Laplace operator (∇²) in hemispherical coordinates, we obtain ∇²p = (1/r²) (∂/∂r) (r² ∂p/∂r). Simplifying this expression, we arrive at ∂²p/∂r² + (1/r) ∂p/∂r.
In both cases, the term ϕμC/k ∂p/∂t represents the source or sink term, where ϕ is the porosity, μ is the fluid viscosity, C is the compressibility, k is the permeability, and ∂p/∂t is the change in pressure over time.
These equations are commonly used in fluid mechanics and petroleum engineering to describe radial flow behavior in spherical and hemispherical geometries, respectively.
To learn more about partial derivative, click here: brainly.com/question/2293382
#SPJ11
Match each probability word to the probability. *Each will be used once*
Impossible 0
Unlikely 7/8
50/50 chance 1/3
Likely 1
Certain 1/2
Answers
Unlikely-1/3
50/50 Chance-1/2
Likely-7/8
Certain-1
What is the value of the expression below when w = 3?
4w2 – 7w – 8
Answers
Step-by-step explanation:
w=3
4w^2-7w-8
4*3^2-7*3-8
4*9-21-8
4*9-29
36-29
7
hope this helps
Answer:
7
Step-by-step explanation:
The area of the shaded sector is shown.

Answers
Answer:
3.99
Step-by-step explanation:
The total sum of central angle of circle is 360 which mean the area of the circle = (12.36 x 360)/89
A=πr^2
=> (12.36 x 360)/89 = 3.14(r^2)
r^2 = 15.92
r = 3.99
Which equation represents a line with slope of 7 and
y-intercept of -1?
Answers
The equation representing a line with a slope of 7 and a y-intercept of -1 is y = 7x - 1.
In the slope-intercept form of a linear equation, y = mx + b, where m represents the slope and b represents the y-intercept. Given that the slope is 7 and the y-intercept is -1, we can substitute these values into the equation to obtain the equation of the line.
Therefore, the equation representing the line with a slope of 7 and a y-intercept of -1 is y = 7x - 1. This equation indicates that for any given value of x, y will be equal to 7 times x minus 1. The slope of 7 indicates that for every unit increase in x, y will increase by 7 units, and the y-intercept of -1 signifies that the line intersects the y-axis at the point (0, -1).
Learn more about slope here:
https://brainly.com/question/3605446
#SPJ11
the region bounded by f(x)=6(4−x)− 1 3 and the x-axis on the interval [0,4) is revolved about the y-axis.
Answers
To find the volume of the solid formed by revolving the region bounded by f(x)=6(4−x)−1/3 and the x-axis on the interval [0,4) about the y-axis, we can use the cylindrical shell method.
First, we need to determine the height of each cylindrical shell. Since we are revolving the region about the y-axis, the height of each shell will be the value of the function f(x) at a given x-value. So, the height of each shell will be: h(x) = 6(4−x)−1/3, Next, we need to determine the radius of each cylindrical shell. The radius of each shell will be the distance from the y-axis to a given x-value, which is simply the x-value itself. So, the radius of each shell will be: r(x) = x.
Now, we can use the formula for the volume of a cylindrical shell: V = 2πrh(x)Δx, where Δx is the width of each shell. Since the interval is [0,4), we can break it up into small intervals of width Δx and sum up the volumes of all the shells: V = ∫0^4 2πrh(x)dx, = ∫0^4 2πx[6(4−x)−1/3]dx. This integral can be evaluated using integration techniques (such as substitution) to obtain the final answer for the volume of the solid.
To know more about function click here
brainly.com/question/28193995
#SPJ11
James takes out a loan of 9000 euros which keeps on charging simple interest at a rate of 3% of the original amount per annum until it is cleared. James pays of 770 euros each year to reduce the loan. After how many years will James have fully cleared the loan?
Answers
James will fully clear the loan after approximately 12 years when the remaining balance reaches zero.
To determine the number of years it will take for James to fully clear the loan, we need to calculate the remaining balance after each payment and divide the initial loan amount by the annual payment until the remaining balance reaches zero.
The loan amount is 9000 euros, and James pays off 770 euros each year. Since the interest is charged at a rate of 3% of the original amount per annum, the interest for each year will be \(0.03 \times 9000 = 270\) euros.
In the first year, James pays off 770 euros, and the interest on the remaining balance of 9000 - 770 = 8230 euros is \(8230 \times 0.03 = 246.9\)euros. Therefore, the remaining balance after the first year is 8230 + 246.9 = 8476.9 euros.
In the second year, James again pays off 770 euros, and the interest on the remaining balance of 8476.9 - 770 = 7706.9 euros is \(7706.9 \times 0.03 = 231.21\) euros. The remaining balance after the second year is 7706.9 + 231.21 = 7938.11 euros.
This process continues until the remaining balance reaches zero. We can set up the equation \((9000 - x) + 0.03 \times (9000 - x) = x\), where x represents the remaining balance.
Simplifying the equation, we get 9000 - x + 270 - 0.03x = x.
Combining like terms, we have 9000 + 270 = 1.04x.
Solving for x, we find x = 9270 / 1.04 = 8913.46 euros.
For more such questions on loan
https://brainly.com/question/25696681
#SPJ8
The sum of the digits of a positive 2-digit number is 12. The units digit is 3 times the tens digit. Find the number
Answers
The sum of the digits is 12:
x + y = 12
The units digit is 3 times the tens digit:
y = 3x
To find the number, we need to find the values of x and y that satisfy both equations simultaneously.
From equation (2), we can substitute the value of y in equation (1):
x + 3x = 12
4x = 12
x = 3
Substituting the value of x back into equation (2):
y = 3 * 3
y = 9
Therefore, the number is 39.
A high school club is researching a tour package offered by the Kayak company. The company charges $35 per person and $245 for the tour guide which function represents the total cost, c(x) of this kayak tour package for the x club members?

Answers
We are given that a tour company charges $35 per person. If the number of persons is "x", then the product of the price per person by the number of people is the cost to pay for the number of people. To this cost we must add the cost of the tour guide, therefore, a function that models the total cost is:
\(C(x)=35x+245\)For every person, the company charges $35. Therefore, the cost for x people can be written as 35x.
The company charges another $245 for the tour guide to the additional cost.
We have the final function :
C(x) = 35x + 245.
make a 3-d surface plot of the function z = cos(x)cos(,./x2 y2)e-i0.2xl in the domain -21t x 21t and -1t y 1
Answers
We can create a 3D surface plot of the function z = cos(x)cos(y)\(e^{-i0.2x}\) in the domain -2π ≤ x ≤ 2π and -π ≤ y ≤ π by using softwares such as MATLAB, Python (with Matplotlib), or Wolfram Alpha.
To make a 3D surface plot of the function z = cos(x)cos(y)e^(-i0.2x) in the domain -2π ≤ x ≤ 2π and -π ≤ y ≤ π, please follow these steps,
1. Identify the function and domain: The function is z = cos(x)cos(y)e^(-i0.2x), and the domain is -2π ≤ x ≤ 2π for x and -π ≤ y ≤ π for y.
2. Choose a software or tool to create the plot: There are several software and tools available to create 3D surface plots, such as MATLAB, Python (with Matplotlib), or Wolfram Alpha.
3. Define the function in the chosen software/tool: Input the given function into the software, and make sure it is properly formatted.
4. Define the domain in the chosen software/tool: Specify the range for x and y, which is -2π to 2π for x, and -π to π for y.
5. Create the 3D surface plot: Use the plotting function in the chosen software/tool to generate the 3D surface plot of the given function within the specified domain.
6. Analyze the plot: Once the plot is generated, you can analyze the characteristics of the function and visualize how it behaves in the given domain.
By following these steps, you will be able to create a 3D surface plot of the function z = cos(x)cos(y)e^(-i0.2x) in the domain -2π ≤ x ≤ 2π and -π ≤ y ≤ π.
Learn more about "MATLAB": https://brainly.com/question/30891746
#SPJ11
a group of clerks must sort 1775 files. each clerk sorts at the constant rate of 30 files per hour. some of the clerks stop working at the end of the first hour; the same number of clerks stop working at the end of the second hour; and the same number of clerks stop working at the end of the third hour. the group finishes the sorting in 3 hours and 10 minutes. find the number of files sorted during the first one and a half hours of sorting.
Answers
The number of files sorted in the first one and a half hours of sorting is 945.
Here, we are given that a group of clerks must sort 1775 files.
Each clerk sorts at a constant rate of 30 files per hour.
Let the number of clerks who start working initially be x.
Thus, they will sort 30x files in the first hour.
After the first hour, let the number of clerks who stop working be a
Thus, the number of files sorted in the second hour will be 30(x - a)
Similarly, the number of files sorted in the third hour will be 30(x - 2a)x
In the last 10 minutes, the number of files sorted will be 5(x - 3a)
Thus, we can form the following equation-
30x + 30(x - a) + 30(x - 2a) + 5(x - 3a) = 1775
30x + 30x - 30a + 30x - 60a + 5x - 15a = 1775
95x - 105a = 1775
19x - 21a = 355
x = (355 + 21a)/ 19
since x and a both have to be integers, (355 + 21a) must be divisible by 19.
This is the case when a = 3
⇒ x = (355 + 21*3)/ 19
x = 418/ 9
x = 22
Now, the number of files sorted in first one and a half hours will be-
30x + 15(x - a)
= 30*22 + 15(22 - 3)
= 660 + 15*19
= 660 + 285
= 945
Thus, the number of files sorted in the first one and a half hours of sorting is 945.
Learn more about remainders here-
https://brainly.com/question/25289437
#SPJ4
Given Boolean function F1=x
yz
z
′
a. Transform from an algebraic expression into a logic diagram b. Create the truth table for each computational step based on precedence 2. Given Boolean function F2=xy
′
+z a. Transform from an algebraic expression into a logic diagram b. Create the truth table for each computational step based on precedence 3. Given Boolean function F3=xy
′
+x
′
z a. Transform from an algebraic expression into a logic diagram b. Create the truth table for each computational step based on precedence 4. Given Boolean function F4=x
′
y
′
z+x
′
yz+xy
′
a. Transform from an algebraic expression into a logic diagram b. Create the truth table for each computational step based on precedence
Answers
1.a. Algebraic expression to a logic diagram:
Here is the Boolean function
F1=x yz z ′ transformed from an algebraic expression into a logic diagram:
1.b. Truth table for each computational step based on precedence:
Given, Boolean function F1=x yz z′
Using the truth table, we can determine the values of each computational step.
The precedence order is parentheses, NOT, AND, and finally OR. Here are the truth tables for each computational step:
2.a. Algebraic expression to a logic diagram:
Here is the Boolean function F2=xy′+z transformed from an algebraic expression into a logic diagram:
2.b. Truth table for each computational step based on precedence:
Given, Boolean function F2=xy′+z
Using the truth table, we can determine the values of each computational step.
The precedence order is parentheses, NOT, AND, and finally OR.
Here are the truth tables for each computational step:
3.a. Algebraic expression to a logic diagram:
Here is the Boolean function F3=xy′+x′z transformed from an algebraic expression into a logic diagram:
3.b. Truth table for each computational step based on precedence:
Given, Boolean function F3=xy′+x′z
Using the truth table, we can determine the values of each computational step.
The precedence order is parentheses, NOT, AND, and finally OR. Here are the truth tables for each computational step:
4.a. Algebraic expression to a logic diagram:
Here is the Boolean function F4=x′y′z+x′yz+xy′ transformed from an algebraic expression into a logic diagram:
4.b. Truth table for each computational step based on precedence:
Given, Boolean function F4=x′y′z+x′yz+xy′Using the truth table, we can determine the values of each computational step.
The precedence order is parentheses, NOT, AND, and finally OR. Here are the truth tables for each computational step:
Thus, the required solution is given above.
https://brainly.in/question/35847222
#SPJ11
for what values of a are the following expressions true:|a+5|=a+5
Answers
Answer:
|a+5|=a+5
Step-by-step explanation:
if a>-5 or a= -5 |a+5|=a+5
if a< -5 |a+5|= -a-5
