Regina has a bag of marbles that contains 3 blue marbles, 4 red marbles, and 5 yellow marbles. She draws one marble, then replaces it, and draws one more.
There are
possible outcomes.
The probability the first drawn marble will be blue is
.
The probability the second marble drawn will be yellow is
.
So, P(blue, then yellow) =
.
Answers
Answer: 12, 1/4, 5/12, 5/48
Step-by-step explanation:
i got it right
Answer:
12,
1/4,
5/12,
5/48
Step-by-step explanation:
Have a great day!
Related Questions
Can someone help me with this. Will Mark brainliest.

Answers
That would be central angels !
Please mark me, I'd like to get to virtuoso.
Find the length of the missing side of the right triangle.
24 ft
7 ft
O 25 ft
O 31 ft
O 22.96 ft
O 625 ft
Answers
Answer:
25 ft
Step-by-step explanation:
Side² = 24² + 7² = 625
√625 = 25 ft
Kevin is tiling his bathroom. The floor is 6-by-5 feet, minus a 2-by-2.5-feet vanity. The tiles he likes are 1-by-1 foot. If he plans to buy 10 percent extra for
waste, how many tiles will he need?
Answers
Answer: He plans to buy 28 tiles.
Step-by-step explanation:
Given: Dimensions of floor = 6-by-5 feet
Since area of rectangle = length x width
Then , area of floor = 6 x 5 square feet = 30 square feet
Dimension for vanity 2-by-2.5-feet , area of vanity = 2 x 2.5 sq. feet = 5 sq. feet
Area of floor for tiling = 30 square feet - 5 sq. feet
= 25 square feet
Area of 1 tile = 1 x 1 = 1 square feet
Number of tiles required to cover 25 sq. feet = 25÷1=25
10 percent extra = 10% of 25+25 = 2.5+25=27.5 ≈28
Hence, he plans to buy 28 tiles.
Giải phương trình lượng giác sau
sin2x+cos2x+sin4x=1
Answers
Answer:
2
Step-by-step explanation:
Given, cosx+cos
2
x=1
⇒cosx=1−cos
2
x
⇒cosx=sin
2
x
Squaring both sides we get
⇒cos
2
x=sin
4
x .....(1)
⇒sin
4
x−cos
2
x=0
Adding both side 1, we get
⇒sin
4
x+1−cos
2
x=1
∴sin
2
x+sin
4
x=1 Proved.
what is the perimeter of the entire design
Answers
First full question is this: What is the perimeter of the entire design?
Cameron makes a quilt design using four congruent
triangles as shown below.
ooo
O 46 cm
O 64 cm
O 108 cm
O 147 cm
9 cm
14 cm.
ANSWER: B) 64
Use the quadratic model y=-4x^2-3x+4 to predict y if x equals 5
Answers
Answer:
y = -4x^2 - 3x + 4
x = 5
y = -4(5)^2 - 3(5) + 4
y = -4(25) - 15 + 4
y = -100 - 15 + 4
y = -114
Step-by-step explanation:
The value of the square root of 13 is between
Answers
Answer:uhhhhhhhhhhhhhhhhhhh 14
Step-by-step explanation:
What is the slope of the line tangent to the curve y^3-xy^2+x^3=5 at the point (1,2)?
Options are as follows: A. 1/10
B. 1/8
C. 5/12
D. 11/4
Answers
The slope of the line tangent to the curve y³-xy²+x³=5 at the point (1,2) is option (B) 1/8.
To find the slope of the line tangent to the curve at the point (1,2), we first need to find the derivative of the curve with respect to x, and then evaluate it at x=1, y=2.
Taking the derivative of both sides of the equation y³-xy²+x³=5 with respect to x using the product rule, we get
3y²(dy/dx) - y² - 2xy(dy/dx) + 3x² = 0
Simplifying this expression and solving for dy/dx, we get:
dy/dx = (y² - 3x²)/(3y² - 2xy)
Substituting x=1 and y=2, we get:
dy/dx = (2² - 3(1)²)/(3(2)² - 2(1)(2))
dy/dx = (4 - 3)/(12 - 4)
dy/dx = 1/8
Therefore, the correct option is (B) 1/8
Learn more about slope here
brainly.com/question/30577296
#SPJ4
Find equation of the line that passes through points A and B

Answers
Answer:
y = 2x + 5
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
calculate m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = A (1, 7 ) and (x₂, y₂ ) = B (- 3, - 1 )
m = \(\frac{-1-7}{-3-1}\) = \(\frac{-8}{-4}\) = 2 , then
y = 2x + c ← is the partial equation
to find c substitute either of the 2 points into the partial equation
using (1, 7 )
7 = 2(1) + c = 2 + c ( subtract 2 from both sides )
5 = c
y = 2x + 5 ← equation of line
A 22-foot ladder is placed against a vertical wall of a building, with the bottom of the ladder standing on level ground 19 feet from the base of the building. How high up the wall does the ladder reach?
Answers
Answer:
3 Feet
Step-by-step explanation:
The reason why it is 3 Feet is that 22 - 19 = 3. (Another anwser is 19 + 3 = 22)
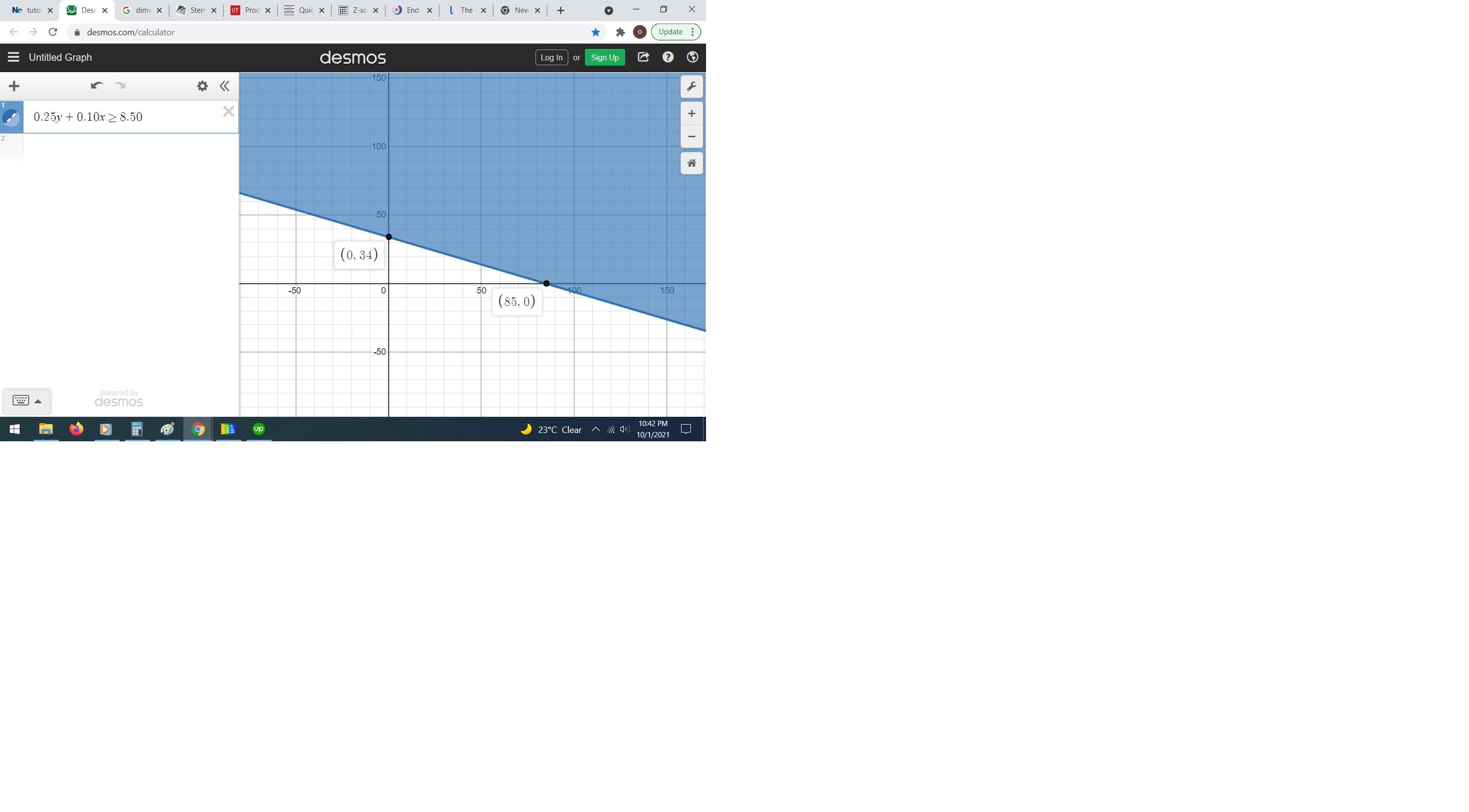
4. Tyler filled a small jar with quarters and dimes and donated it to his school'scharity club. The club member receiving the jar asked, "Do you happen toknow how much is in the jar?" Tyler said, "I know it's at least $8.50, but I don'tknow the exact amount."4a. Write an inequality to represent the relationship between the numberof dimes, d, the number of quarters, q, and the dollar amount of the moneyin the jar.
Answers
Let
y -----> number of quarters
x ----> number of dimes
we have that
the inequality that represents this situation is
Remember that
1 quarter =$0.25
1 dime=$0.10
so
\(0.25y+0.10x\ge8.50\)rewrite the variables
\(0.25q+0.10d\ge8.50\)see the attached figure to better understand the problem
Part 4b
The solution of the given inequality is the shaded area above the solid line 0.25q+0.10d=8.50
A solution to this inequality could be the point (50,50)
that means
the number of quarters is 50 and the number of dimes is 50
the ordered pair must satisfy the inequality
Verify
\(\begin{gathered} 0.25q+0.10d\ge8.50 \\ 0.25(50)+0.10(50)\ge8.50 \\ 12.50+5\text{ }\ge8.50 \\ 17.50\text{ }\ge8.50\text{ --}\longrightarrow\text{ is ok} \end{gathered}\)Part 4c
we have that
d=25 dimes
substitute in the inequality and solve for q
so
\(0.25q+0.10(25)\ge8.50\)solve for q
\(\begin{gathered} 0.25q+2.5\ge8.50 \\ 0.25q\ge8.50-2.5 \\ 0.25q\ge6 \\ q\ge24 \end{gathered}\)the number of quarters must be greater than or equal to 24
Help please I cant figure it out.

Answers
1/6 = 0.166 x 100 = 16.6%
URGENT 50 PTS
In ALMO, Point C is the intersection of the blue and green segments. If CM = 11, QM = 5, PL = 6, RM = 10, CO =9.8, and LC = 2x + 5, solve for X

Answers
explanation:
You run the perimeter of a baseball field at a rate of 9 feet per second.how long does it take you to run the baseball field to the nearest tenth of a second?
Answers
The answer to the nearest tenth of a second is 40.0 seconds.
To solve this problem, we need to know the length of the perimeter of a baseball field. According to official regulations, the distance between each base is 90 feet, so the perimeter of a baseball field is 360 feet.
Now, we can use the formula distance = rate x time, where distance is 360 feet, and rate is 9 feet per second. We can solve for time by dividing both sides of the equation by the rate:
time = distance / rate
time = 360 / 9
time = 40 seconds
Therefore, it takes you 40 seconds to run the perimeter of the baseball field. To find the answer to the nearest tenth of a second, we need to round the answer. Since the next decimal place after the tenths is a hundredth, we need to look at the second decimal place. If it is 5 or greater, we round up, otherwise, we round down. In this case, the second decimal place is 0, so we round down. Therefore, the answer to the nearest tenth of a second is 40.0 seconds.
Learn more on nearest tenth here:
https://brainly.com/question/12102731
#SPJ11
Is the relationship between volume and moles of gas proportional or inversely proportional?
Answers
The volume of the gas approximately directly proportional to its number of moles of gas when both temperature and pressure are constant.
Explain the Mole-Volume Relationship - Avogadro’s Law?The volume of a gas being directly proportional to the amount of moles of that gas, according to a plot illustrating the relationship between temperature and volume of a gas under constant pressure. Avogadro's law is cited in support of this: When the pressure (P) and temperature (T) are constant, the volume (V) of an ideal gas (n) directly varies depending on the number of moles of the gas (n).V∝ n at constant P and T
V = constant × (n)
Vn = constant
This can be mathematically stated as follows: As before, we can anticipate what will change to the volume of the a sample of gas as we adjust the number of moles using Avogadro's law.
To know more about the Avogadro’s Law, here
https://brainly.com/question/26931664
#SPJ4
Factor the expression using the greatest common factor
2x + 10 =
Answers
Answer:
2(x+5)
Step-by-step explanation:
2x+10
1.Factor our the 2 from the equation
2.Your answer after will be 2(x+5)
Answer:
Step-by-step explanation:
The path of a drinking fountain is designed to reach a maximum height of 4.5 feet after 1 second. The spout is at a height of 4 feet. If the water pressure decreases, the water does not reach the intended height. Complete the values for the inequality in vertex form to describe the points that are less than the projected path. y__a(x – h)2 + k
a=
h=
k=
Answers
The values for the inequality in vertex form is y < -1.5(x - 1)^2 + 4.5
How to determine the equation of the parabolaThe equation for a parabolic function in vertex form is given by y = a(x - h)^2 + k, where (h, k) is the vertex of the parabola.
The vertex of the parabolic path of the drinking fountain is (1, 4.5). So, h = 1 and k = 4.5.
Substituting the values for h and k into the equation:
y = a(x - 1)^2 + 4.5
Now, we need to determine the value of a using the point
(x, y) = (2, 4)
So, we have
a(2 - 1)^2 + 4.5 = 4
Evaluate
a = -1.5
So, we have
y = -1.5(x - 1)^2 + 4.5
Express as inequality
y < -1.5(x - 1)^2 + 4.5
Read more about parabola at
https://brainly.com/question/1480401
#SPJ1
Complete question
The path of a drinking fountain is designed to reach a maximum height of 4.5 feet after 1 second. The spout is at a height of 4 feet after 2 seconds. If the water pressure decreases, the water does not reach the intended height. Complete the values for the inequality in vertex form to describe the points that are less than the projected path. y__a(x – h)2 + k
Answer:
Step-by-step explanation:
The path of a drinking fountain is designed to reach a maximum height of 4.5 feet after 1 second. The spout is at a height of 4 feet. If the water pressure decreases, the water does not reach the intended height.
Complete the values for the inequality in vertex form to describe the points that are less than the projected path.
y
✔ <
a(x – h)2 + k
a =
✔ –0.5
h =
✔ 1
k =
✔ 4.5
The total cost of Anja’s trip to the dentist was $628.35. She paid a flat fee of $89.95 which included the checkup and cleaning and then had 4 cavities filled, each of which cost the same amount. Which shows the correct equation and value of x, the cost of each cavity filling?
a 4 x + 89.95 = 628.35; x = 134 dollars and 60 cents
b 4 (89.95) + x = 628.35; x = 268 dollars and 55 cents
c 4 x + 89.95 = 628.35; x = 179 dollars and 58 cents
d 4 (89.95) + x = 628.35; x = 538 dollars and 40 cents
Answers
|| ▼ Answer ▼ ||
Option (A) 4 x + 89.95 = 628.35; x = 134 dollars and 60 cents
|| ✪ Solution ✪ ||
Total cost of the trip was $628.35, Anja paid $89.95 as a flat fee, and paid extra for the four tooth fillings, the equation that represents this situation is:
\(4x+89.95=628.35-- > (1)\)
The solution to equation (1) is as follows:
\(4x=628.35-89.95=538.4\)
\(x=\frac{538.4}{4} =134.6\)
\(x=134.6\)
x = $134 and 60 cents
Conclusion: The answer is Option (a).
Hope this helps!
If you have any queries please ask.
10 is what percentage of 50 
Answers
Answer:
20%
Step-by-step explanation:
10 of 50 can be written as:1050To find percentage, we need to find an equivalent fraction with denominator 100. Multiply both numerator & denominator by 1001050 × 100100= (10 × 10050) × 1100 = 20100 Therefore, the answer is 20%
The area of castles roof is 985 square feet.If shingles cost $12.50 per square foot, how much money would a cost to completely cover the roof?
Answers
Answer:
Step-by-step explanation:
Since there are 985 square feet to cover, and it costs 12.50 per square foot, you multiply 12.50 by 985 to get 12,312.50, the total cost and answer.
How do you graph a square root graph?
Answers
Answer:
Determine the domain of the function.
Pick x-values in the domain of the function, and find the y-values that correspond with them. (An endpoint of the domain is a helpful value to pick.)
Plot the points and draw the graph.
Step-by-step explanation:
ANSWERS:
positive linear
negative linear
nonlinear
no relationship

Answers
Answer:
Step-by-step explanation:
No relationship i belive
Step by step explanation
10 people were trying to be one of the first 5 callers to a radio station. how many different sets of people couldhave succeeded?
Answers
Formula to calculate combinations is given by -
nCr=[n !]/[r ! * (n-r) !]
where,
nCr = number of combinations
n = total number of objects in the set
r = number of choosing objects from the set
Now, according to given -
n = 10 people
r = 5 callers
Hence,
Number of possible combinations = nCr
= 10C5
= (10!)/[5! * (10-5)!]
= 252
Thus, 252 different people could have made successful calls to the radio station.
Learn more about combinations at : https://brainly.in/question/16513304
#SPJ4
Use Descartes' Rule of Signs to determine how many positive and how many negative real zeros the polynomial can have. Then determine the possible total number of real zeros. (Enter your answers as comma-separated lists.)
P(x) = x^3 − x^2 − x − 5
number of positive zeros possible number of negative zeros possible number of real zeros possible
Answers
According to Descartes' Rule of Signs, there is 1 positive real zero and 2 or 0 negative real zeroes of the polynomial.
Descarte's Rule of Signs determines the number of real zeros in polynomial functions.
This indicates that -
The number of positive real zeros in the polynomial function f(x) is less than or equal to an even number depending on the sign change of the coefficients.
The number of negative real zeros in f(x) is an even number equal to or less than the number of sign changes of the coefficients of f(-x) terms.
Here, the polynomial function is given as -
\(P(x)=x^{3}-x^{2} -x-5\) ----- (1)
We have to find out the number of positive and negative real zeros that the given polynomial can have.
The given polynomial already has its variables in the descending powers. So, we can easily determine the number of sign changes in the coefficients of P(x).
So, the coefficients of the variables in P(x) are -
1, -1, -1, -5
From above, we see that -
There is a sign change in the first and second variable coefficients
There is no sign change in the second and third variable coefficients
There is no sign change in the third and fourth variable coefficients
According to Descartes' Rule of Signs, there can be exactly three positive real zeros or less than three but an odd number of zeros.
So, we can determine that the number of positive real zeroes of the given polynomial can be 1.
To find out the negative real zeroes of the given polynomial, we have to find out P(-x) and determine the sign changes in the variable coefficients of P(-x).
From equation (1), we can write P(-x) as -
\(P(x)=x^{3}-x^{2} -x-5\\= > P(-x)=(-x)^{3}-(-x)^{2} -(-x)-5\\= > P(-x)=-x^{3}-x^{2} +x-5\)----- (2)
So, the coefficients of the variables in P(-x) are -
-1, -1, +1, -5
From above, we see that -
There is no sign change in the first and second variable coefficients
There is a sign change in the second and third variable coefficients
There is a sign change in the third and fourth variable coefficients
According to Descartes' Rule of Signs, since there are two sign changes of the coefficient variables, there can be two negative real zeros or less than two but an even number of zeros.
So, we can determine that the number of negative real zeroes of the given polynomial can be 2 or 0.
Thus, according to Descartes' Rule of Signs, there is 1 positive real zero and 2 or 0 negative real zeroes of the polynomial.
To learn more about Descartes' Rule of Signs visit https://brainly.com/question/28747313
#SPJ4
Which expression is equivalent to the expression -3(4x - 2) - 2x
A) -8x
B) -16x
C) -14x - 2
D) -14x + 6
Answers
Answer:
-14x + 6 (option D)
Step-by-step explanation:
To solve the given equation, you first need to distribute the negative 3.
So, you need to multiply
(4x)(-3) ; (-2)(-3)
(4x)(-3)= -12x
(-2)(-3)= 6
So, your new, distributed, equation would be:
-12x + 6 - 2x
If we combine like terms (-12x - 2x), our new equation will be:
-14x + 6
In the first half of a basketball game, a player scored 9 points on free throws and then scored a number of 2-point shots. In the second half, the player scored the same number of 3-point shots as the number of 2-point shots scored in the first half. Which expression represents the total number of points the player scored in the game?
Answers
This question is incomplete
Complete Question
In the first half of a basketball game, a player scored 9 points on free throws and then scored a number of 2-point shots. In the second half, the player scored the same number of 3-point shots as the number of 2-point shots scored in the first half. Which expression represents the total number of points the player scored in the game?
a) 2x + 3x + 9
b) 2x + 3 + 9
c) 2x + 3x + 9x
d) 2 + 3x + 9
Answer:
a) 2x + 3x + 9
Step-by-step explanation:
Let the number of points shots a player scores = x
In a free throw, the player scored 9 points = 9
The player also scored a number of 2-point shots = 2x
In the second half, the player scored the same number of 3-point shots as the number of 2-point shots scored in the first half = 3x
The expression represents the total number of points the player scored in the game =
2x + 3x + 9
What is the diameter of the small volcano "Pico" at the \( 2000 \mathrm{~m} \) isoline? (meters) Remember \( 1 \mathrm{~km}=1000 \mathrm{~m} \)
Answers
The diameter of the small volcano 'Pico' would be = 8km
What is an isoline of a map?An isoline is defined as the line found on a map that has constant value of either distance, temperature or rainfall.
The isoline that is used in the given map above = 2000m.
The number of lines that surrounds the pico volcano = 4
Therefore the diameter of the volcano = 2000×4 = 8000m
But 1000m = 1km
8000m = 8km
Learn more about diameter here:
https://brainly.com/question/30460318
#SPJ4

3. Mary Ann drove 120 miles north to visit her grandmother. After her visit, she returned home driving south. Shedecided to visit a friend and drove 212 miles south to her friend's house. How far is she from her starting positionbefore she visited her grandmother?This is due today!!
Answers
ANSWER
92 miles
EXPLANATION
Let us make a sketch to represent the problem:
From the diagram, A is the starting point, B is the point she met her grandmother and C is the point she met her friend.
To find how far she is from her starting point, we have to simply subtract AB from BC.
That is:
BC - AB
= 212 - 120
= 92 miles
That is how far she is from her starting position.

The main scale of a vernier callipers reads 10 mm in 10 divisions. 10 divisions of Vernier scale coincide with 9 divisions of the main scale. When the two jaws of the callipers touch each other, the right of zero of main scale. When a cylinder is tightly placed between the two jaws, the zero of vernier scale lies slightly to the left of 3.2 cm and the fourth vernier division coincides with a main scale division. The diameter of the cylinder is.
A 3.09 cm
B 3.9 cm
C 3.90 cm D 39mm
Answers
The answer will be option C (3.90 cm).
To find the diameter, we need to determine the exact length reading on the main scale and then add the Vernier scale reading. We know that 10 divisions of the Vernier scale coincide with 9 divisions of the main scale.
If the zero of the Vernier scale lies slightly to the left of 3.2 cm on the main scale, then we can assume that it lies between the 3rd and 4th division of the main scale. Since the 4th division of the Vernier scale coincides with a main scale division, we can determine that the length reading on the main scale is 3.3 cm.
Next, we need to determine the Vernier scale reading. Since the 4th division of the Vernier scale coincides with a main scale division, the reading on the Vernier scale is 0.1 cm. Adding the main scale reading (3.3 cm) and the Vernier scale reading (0.1 cm), we get a total length reading of 3.4 cm.
Since the cylinder is tightly placed between the jaws of the callipers, we can assume that this length reading is equal to the diameter of the cylinder. Therefore, the diameter of the cylinder is 3.4 cm. The answer is closest to option C (3.90 cm).
Here you can learn more about diameter
https://brainly.com/question/297647#
#SPJ11
Solve the inequality 4x - 6 > 6x - 20.
Ox>7
0x<7
0x<2
Ox> 2
Answers
Answer:
7>0x
0x<7
Step-by-step explanation:
4x-6>6x-20
-6>2x-20
14>2x
7>x