repeat (t), do (z) means "repeat z for t number of times"
what does this mean?
Answers
The phrase "repeat (t), do (z)" means to perform a certain action or set of actions, represented by the instruction or code in (z), a specified number of times, as determined by the value of (t).
In other words, the action in (z) is repeated or executed iteratively for a specific number of times as determined by the value of (t).
For example, if (t) is equal to 5 and (z) is a set of instructions to print the phrase "Hello, world!", the phrase "Hello, world!" would be printed 5 times. The syntax used in the phrase is commonly used in computer programming and other technical fields to indicate a loop or iterative process.
To know more about specific number of times:
https://brainly.com/question/29690694
#SPJ4
Related Questions
Which postulate can be used to prove the two triangles are congruent?

Answers
Answer:
SAS
Step-by-step explanation:
If two sides and the included and the included angle of one triangle are congruent to two sides and the included angle of another triangle , then the triangles are congruent. The included angle is the angle formed by the two sides.
EF = BC
∠ F = ∠ C
DF = AC
then the two triangles are congruent by the SAS postulate.
Answer:
SAS
Step-by-step explanation:
On triangle one and two, they both start by having a congruent side, then a congruent angle, then another congruent side, thus making these triangles congruent by Side Angle Side.
It can't be AAS because there is only one angle, we know is congruent.
It can't be SSS because there are only two sides, we know are congruent.
It can't be HL because there is no right angle, meaning these aren't right triangles.
-22 = -8 + 9(a - 2)
XD
Answers
Answer: a=4/9
Step-by-step explanation: math
love how everyone hw on here is geometry and im just here like.... help...

Answers
Answer:
nope it isn't a linear function
Step-by-step explanation:
if you put it in a graph it isn't a straight line
2. State the domain, range, asymptotes and graph the following function 4x - 3 f(x) = x+4
Answers
Domain of this function is alll real numbers,range of this fuction is all real numbers,Asymptotes of this fuction is that there are no vertical or horizontal asymptotes and the graph in Linear function.
The given function is f(x) = 4x - 3/(x + 4). To determine the domain of this function, we need to consider any values of x that would make the denominator, x + 4, equal to zero. However, since division by zero is undefined, we exclude x = -4 from the domain. Therefore, the domain of the function is all real numbers except x = -4.
Next, let's determine the range of the function. Since the function is a rational function, it can take any real value except the values that would make the numerator zero. In this case, the numerator is 4x - 3, which can never be equal to zero for any real value of x. Therefore, the range of the function is also all real numbers.
Moving on to the asymptotes, we can analyze the behavior of the function as x approaches positive or negative infinity. Since the degree of the numerator is less than the degree of the denominator, the function has a horizontal asymptote. However, in this case, the degree of the numerator is equal to the degree of the denominator, resulting in a slant asymptote rather than a horizontal asymptote. To find the equation of the slant asymptote, we can perform long division or synthetic division on the function. Upon doing so, we find that the slant asymptote is y = 4x - 7.
Finally, since the function is a linear function (degree 1), the graph will be a straight line. The graph will approach the slant asymptote as x approaches positive or negative infinity, but it will not have any vertical or horizontal asymptotes.
Learn more about Functions
brainly.com/question/21145944
#SPJ11
Seth owns a local ice cream parlor. He designed a new sign in the shape of an ice cream cone and cut it from plywood. He wants to attach LED lights around the PERIMETER of the sign. A diagram of the sign made from a TRIANGLE and a SEMICIRCLE is shown below. What is the length of LED lights he will need to span the PERIMETER of the sign?

Answers
Answer:2 feet i think?
Step-by-step explanation:
sorry need points
An ice skater skates completely around the two circles shown in the diagram. Each circle has a diameter of 20 meters. What is the approximate total distance skated by the ice skater? Use 3.14 for π . Round your answer to the nearest meter.
A) 628 meters
B) 251 meters
C) 126 meters
D) 63 meters
Answers
The solution is Option C.
The total distance skated by the ice skater is 126 meters
What is a Circle?
A circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called “centre”. Every line that passes through the circle forms the line of reflection symmetry. Also, the circle has rotational symmetry around the centre for every angle
The perimeter of circle = 2πr
The area of the circle = πr²
where r is the radius of the circle
Given data ,
Let the distance traveled by the skater be = D
Let the diameter of the circle A be = 20m
Let the diameter of the circle B be = 20m
So , the radius of circle A = 10 m
The radius of circle B = 10 m
Now , the value of π = 3.14
So , the distance traveled by the skater = perimeter of circle A + perimeter of circle B
Perimeter of Circle A = 2πr
Substituting the values in the equation , we get
Perimeter of Circle A = 2 x 3.14 x 10
Perimeter of Circle A = 62.8 m
And ,
Perimeter of Circle B = 2πr
Perimeter of Circle B = 2 x 3.14 x 10
Perimeter of Circle B = 62.8 m
Therefore , the distance traveled by the skater = Perimeter of Circle A + Perimeter of Circle B
Substituting the values in the equation , we get
The distance traveled by the skater = 2 x 62.8
The distance traveled by the skater = 125.6 meters
The distance traveled by the skater = 126 meters
Therefore , the value of D is 126 meters
Hence , The total distance skated by the ice skater is 126 meters
To learn more about circle click :
https://brainly.com/question/28391204
#SPJ2
Why is it difficult to solve one verr two minus one over eight without using a common denominator
Answers
To substract two fractions, we have to have common denominators.
For example, if we want to substract 1/3 from 1/2, we have to convert the fractions so they have a common denominator of 6.
The denominators are the ones that give sense to the fraction. In fact, when we substract whole numbers, we can consider we are substracting "fractions of one".
Then, for example, 5 - 4 could have been written as 5/1 -4/1.
If the numbers have different denominators, we can not perform additions or substractions until we express the fractions with the same denominator.
Trying to substract two fractions with different denominators is like substracting two things that are not expressed in the same units and it will yield an incorrect result.
A function g models a relationship in which the dependent variable is multiplied by 9
for every 2 units the independent variable increases. The value of the function at 0 is 2.
Which equation represents g?
Answers
The link represented by function g multiplies the dependent variable by 9 for every increase of 2 units in the independent variable. The equation that represents g is \(g(x)= 2 \times3^x\),and the function has a value of 2 at 0
Let x be the independent variable, and let g(x) be the dependent variable.
According to the problem, for every 2 units the independent variable increases, the dependent variable is multiplied by 9. This suggests an exponential relationship of the form:
\(g(x)= a \times b^x\)
where a is the initial value of the dependent variable (when x=0), and b is the growth factor (how much the dependent variable changes for every unit increase in x).
We are given that g(0) = 2, so we can plug in these values and solve for a:
\(g(0)= a \times b^0\)
a = 2
So now we have:
\(g(x)= 2 \times b^x\)
We still need to find the growth factor b. We are told that the dependent variable is multiplied by 9 for every 2 units the independent variable increases. In other words:
\(g(x+2) = 9 \times g(x)\)
Using our equation for g(x), we can substitute in and simplify:
\(2 \times b(x+2) = 9 \times 2\times b^x\)
Simplifying, we get:
\(b^2\) = 9
Taking the square root of both sides (we take the positive square root since b must be positive in order for g to be an increasing function), we get:
b = 3
So the final equation for g(x) is:
\(g(x) = 2 \times 3^x\)
For more such questions on variable
https://brainly.com/question/25223322
#SPJ4
find the ratio of 2500g to 35kg
Answers
35kg - 3500g
3500g - 2500g
= 1000g
Answer:
1 : 14
Step-by-step explanation:
The measures must have the same units, that is both g or Kg
2500 g : 35 Kg
= 2500 g : 35000 g ( 1 Kg = 1000 g )
Divide both parts by 100
= 25 : 350 ( divide both parts by 25 )
= 1 : 14
help...................

Answers
Answer:
Andre's equation: y=5x+100
Elena's equation: y=20x+10
Step-by-step explanation:
total money (y) = (amount per week) times number of weeks (x) + (starting amount)
to solve number 3, plug in 4 for x in both equations and solve for y.
then find the difference between the two values.
to solve number 4, because both equaions are already set equal to y, you can set them equal to each other so you have 5x+100=20x+10
then solve for x to find number of weeks and plug this value into one of the equations for y to find how much money they have in their bank account.
Let f be the function defined by f(x) For how many values of x in the open interval (0, 1.565) is the instantaneous rate of change of f equal to the average rale of change = of f on the closed interval [0. 1.565] (A) Zero (B) One (C) Three (D) Four
Answers
After finding the derivative of f(x) and setting it equal to the average rate of change, we find that there is only one solution in the open interval (0, 1.565). Therefore, the answer is (B) one
To determine the number of values of x in the open interval (0, 1.565) where the instantaneous rate of change of f is equal to the average rate of change of f on the closed interval [0, 1.565], we can use the Mean Value Theorem for Derivatives.
According to the Mean Value Theorem for Derivatives, if f(x) is a differentiable function on the closed interval [a, b], where a < b, then there exists a point c in the open interval (a, b) such that the instantaneous rate of change of f at c is equal to the average rate of change of f on [a, b].
In this case, we are given that the closed interval is [0, 1.565] and the open interval is (0, 1.565), so we need to find if there exists any point c in (0, 1.565) where the instantaneous rate of change of f is equal to the average rate of change of f on [0, 1.565].
To do this, we can first find the average rate of change of f on [0, 1.565] by using the formula:
average rate of change = (f(1.565) - f(0))/(1.565 - 0)
Next, we can find the derivative of f(x) and set it equal to the average rate of change to find any possible values of c that satisfy the Mean Value Theorem for Derivatives.
To learn more about : average
https://brainly.com/question/130657
#SPJ11
The answer is (C) Three, as there will be three points of intersection.
To answer this question, we need to first understand what the instantaneous rate of change and average rate of change mean. The instantaneous rate of change of a function at a particular point is the slope of the tangent line to the graph of the function at that point. The average rate of change of a function over a closed interval is the slope of the secant line connecting the two endpoints of the interval.
In this case, we are looking for values of x in the open interval (0, 1.565) where the instantaneous rate of change of f is equal to the average rate of change of f over the closed interval [0, 1.565].
Since f(x) is not given, we cannot determine the instantaneous and average rate of change of f directly. However, we can use the Mean Value Theorem for Derivatives to help us solve the problem. The Mean Value Theorem states that if f is a continuous function on the closed interval [a, b] and differentiable on the open interval (a, b), then there exists a number c in the open interval (a, b) such that:
f'(c) = (f(b) - f(a))/(b - a)
In this case, we can apply the Mean Value Theorem to the closed interval [0, 1.565] and the open interval (0, 1.565) to get:
f'(c) = (f(1.565) - f(0))/(1.565 - 0)
Simplifying, we get:
f'(c) = f(1.565)/1.565
So, we need to find values of x in the open interval (0, 1.565) where f(x)/x = f(1.565)/1.565.
To solve this equation, we can graph y = f(x)/x and y = f(1.565)/1.565 on the same set of axes and look for points of intersection. The number of intersection points will be the number of values of x in the open interval (0, 1.565) where the instantaneous rate of change of f is equal to the average rate of change of f over the closed interval [0, 1.565].
Therefore, the answer is (C) Three, as there will be three points of intersection.
Visit here to learn more about Mean Value Theorem;
brainly.com/question/30403137
#SPJ11
. Equivalent Units Calculations—Weighted Average Method Terrace Corporation makes an indus- trial cleaner in two sequential departments, Compounding and Drying. All materials are added at the beginning of the process in the Compounding Department. Conversion costs are added evenly throughout each process. Terrace uses the weighted average method of process costing. In the Com- pounding Department, beginning work-in-process was 2,000 pounds (60% processed), 36,000 pounds were started, 34,000 pounds were transferred out, and ending work-in-process was 70% processed. Calculate equivalent units for the Compounding Department for August 2019.
Answers
The equivalent units for the Compounding Department for August 2019 is 57,000 pounds.
Here is the explanation -
To calculate the equivalent units for the Compounding Department in August 2019 using the weighted average method, we need to consider the units that were started and completed, as well as the ending work-in-process.
Step 1: Calculate the equivalent units for units started and completed:
- 36,000 pounds were started.
- 34,000 pounds were transferred out.
Equivalent units for units started and completed = 34,000 pounds.
Step 2: Calculate the equivalent units for ending work-in-process:
- Ending work-in-process was 70% processed.
- Beginning work-in-process was 2,000 pounds (60% processed).
Equivalent units for ending work-in-process = (70% x Ending work-in-process) + (60% x Beginning work-in-process)
Equivalent units for ending work-in-process = (70% x 2,000 pounds) + (60% x 36,000 pounds)
Equivalent units for ending work-in-process = 1,400 pounds + 21,600 pounds
Equivalent units for ending work-in-process = 23,000 pounds.
Step 3: Calculate the total equivalent units:
Total equivalent units = Equivalent units for units started and completed + Equivalent units for ending work-in-process
Total equivalent units = 34,000 pounds + 23,000 pounds
Total equivalent units = 57,000 pounds.
Therefore, the equivalent units for the Compounding Department for August 2019 is 57,000 pounds.
To know more on Weighted average visit:
https://brainly.com/question/28334973
#SPJ11
If ABCD is a parallelogram, which of the following statements must be true? (

Answers
Answer:
AB=CD and BC=AD because both of them are visually paired with the same longitude.
Answer:
AB = CD, BC = AD
Step-by-step explanation:
According to parallelogram properties,
Angle A = 180-Angle B; False
AB!=BC; False
AC==BD is only true when AB = BC, False
AB ==CD, BC == AD; True
Given: y = 3x - 4. What is the x-intercept? (0, -4) ( 4/3 , 0) (0, 4/3 )
Answers
This equation is in slope-intercept form of y = mx + b form.
The m represented by the coefficient of the x term
represents the slope and b represents the y-intercept.
So our y-intercept is -4 and we can write this as the ordered pair (0, -4).
PLEASEE HELP ME WITH THIS……..

Answers
Answer:
KM/KL = HJ/HI
Step-by-step explanation:
Triangle JIH is similar to MLK due to Angle-Angle similarity. So, KM/KL = HJ/HI
A rainstorm in Portland, Oregon, has wiped out the electricity in about 5% of the households in the city. A management team in Portland has a big meeting tomorrow, and all 6 members of the team are hard at work in their separate households, preparing their presentations. What is the probability that none of them has lost electricity in his/her household? Assume that their locations are spread out so that loss of electricity is independent among their households. Round your response to at least three decimal places. (If necessary, consult a list of formulas.)
Answers
Answer:
Binomial distribution because:
Trials are Bernoulli (affected or not)
Probability is known (p=0.05) and remains constant for all trials.
Number of trials is known (n=6).
P(x)=C(n,x)p^x*(1-p)^(n-x)
x=0 =>
P(0)=C(6,0)(0.05^0)(0.95^6)
=0.7351.... (approximately)
1. Which Quadrant is Point F in?

Answers
Answer:
point f is in quadrant 3 . . .
consider an invertible symmetric n×n matrix a. when does there exist a nonzero vector v in rn such that av is orthogonal to v? give your answer in terms of the signs of the eigenvalues of a.
Answers
If an invertible symmetric n×n matrix A has a nonzero vector v in R^n such that Av is orthogonal to v, then it means that the dot product of Av and v is equal to zero. In other words, Av . v = 0. Using th peroperties of the dot product, we can rewrite this equation as:
v . A^T v = 0
Since A is symmetric, A^T = A, and we can rewrite the equation as:
v . A v = 0
This equation can be further simplified using the properties of the dot product:
v . A v = (A v) . v = 0
From this equation, we can see that the eigenvalues of A must be either positive or negative. If the eigenvalues of A are all positive, then v . A v > 0, which contradicts the equation v . A v = 0. Similarly, if the eigenvalues of A are all negative, then v . A v < 0, which also contradicts the equation v . A v = 0.
Therefore, the only way for there to exist a nonzero vector v in R^n such that Av is orthogonal to v is if the eigenvalues of A are both positive and negative. In other words, A must have both positive and negative
eigenvalues.
Read more about nonzero vector v here:https://brainly.com/question/30301934
#SPJ11
I need help:/
please, and thank you:)
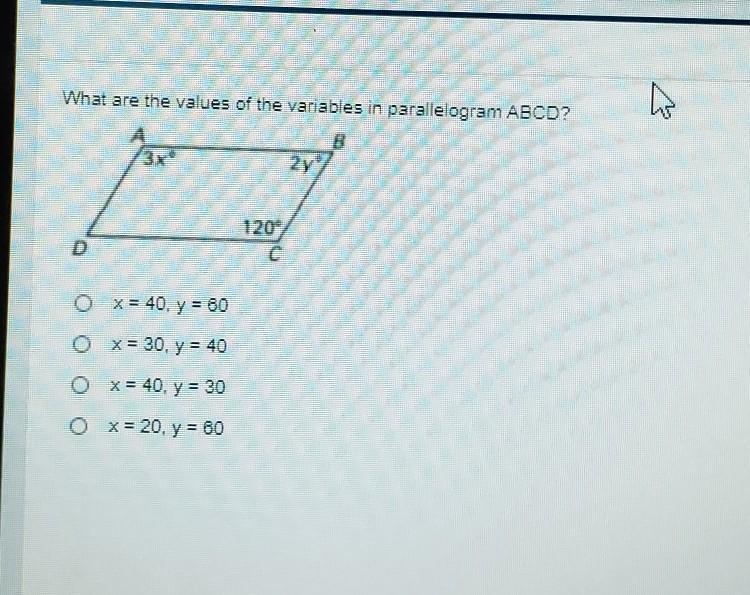
Answers
Answer:
C x=40, y=30
Step-by-step explanation:
Remember the opposite side of parallelogram is the same
so angle C and angle A is the same.
3x=120
divide both sides by 3 and you get 40
All parallelogram equal to 180 degrees so to find y
180=2y+120
-2y=120-180
-2y=-60 negative divide negative is positive.
y=30
The numbers of hours worked (per week) bv 400 statistics students are shown below. a. Create a relative frequency table. b. What is the cumulative percent frequency for students working less than 20 hours per week? c. What is the percentage of students who work at least 10 hours per week?
Answers
An object is moving ata speed of 63 centimeters every 2 days. Express this speed in meters per hour. Round your answer to the nearest hundredth. "Note: you must use these exact conversion factors to get this question right. Distance / length 1 foot (ft) = 12 inches (in) 1 yard (yd) = 3 feet (ft) 1 mile (mi) = 528o feet (ft) 1 meter (m) = 100 centimeters (cm) 1inch (in) = 2.54 centimeters (cm) 1 foot (ft) = 0.305 meters (mn) Time 1 mile (mi) = 1.609 kilometers (km) 1 minute (min) = 60 seconds (sec) 1 hour (hr) = 60 minutes (min) 1 kilometer (km) = 1000 meters (m) 1 month (month) = 30 days (days) 1 day (day) = 24 hours (hr) 1 week (week) = 7 days (days) 1 year (year) = 365 days (days)
Answers
Step-by-step explanation:
the given speed is
63 cm / 2 days
1 m = 100 cm
therefore, m = cm/100.
so,
63 cm = 0.63 m
1 day = 24 h
therefore,
2 days = 24×2 = 48 h
so, we have a speed of
0.63 m / 48 h
we need to get the speed of meters in 1 hour.
so, we need to do a normal fraction operation.
e.g. when we have 43/10, but we want to have 1 in the denominator (bottom part).
what do we do ? well, we divide top and bottom (to keep the total value of the fraction unchanged) by 10 and get
4.3/1 = 4.3
we do the same with
0.63 m / 48 h
as we want to have only 1 hour in the denominator.
we divide top and bottom by 48 :
0.63/48 / 1 h = 0.013125 m/h ≈ 0.01 m/h
what is the measure (in radians) of the angle formed by the hands of a clock at each time? write your answers in terms of π . a. 1:30 p.m.
Answers
The measure (in radians) of the angle formed by the hands of a clock at 1.30 PM is 3π/4 radians.
The given time is 1:30 PM.
Time is used to quantify, measure, or compare the duration of events or the intervals between them, and even, sequence events.
The angle between hour hand and minute hand is 135°.
In radians = 135° ×π/180°
= 9π/12
= 3π/4
Therefore, the measure (in radians) of the angle formed by the hands of a clock at 1.30 PM is 3π/4 radians.
Learn more about time here:
https://brainly.com/question/15356513.
#SPJ6

The value of a new car decreases by about 15% in the first year. How much will a car be worth after one year if its initial value was $1,500? If you get stuck, consider using diagrams or a table to organize your work.
Answers
Answer:
$12,750
Step-by-step explanation: when you do the math you get it your welcome my G
Craig went bowling with $190 to spend. He rented shoes for $ 10.00, paid $20 for food, and paid $10.00 for each game bowled. How many games could Craig bowl?
Answers
(solve for x)
-8-x=x-4x
Answers
Answer:
\( ➜- 8 - x + x = x - 4x + x\)
\( ➜- 8 = - 2x\)
\( ➜- \frac{8}{ - 2} = \frac{ - 2x}{2} \)
\(➜x=4\)
7. The quality control division of Rothschild's Blueberry Farm randomly inspects 100 of the containers in the truck being
sent to Stop and Shop. Identify the population and sample given in this scenario.
Answers
The 100 containers that the quality control division of Rothschild's Blueberry Farm randomly inspects.
Population: The containers of blueberries that are being sent to Stop and Shop.
Sample: The 100 containers that the quality control division of Rothschild's Blueberry Farm randomly inspects.
Therefore, the 100 containers that the quality control division of Rothschild's Blueberry Farm randomly inspects.
Learn more about the random sample here:
https://brainly.com/question/12719656.
#SPJ1
which of the following is the most widely used method for rating attributes?
Answers
The most widely used method for rating attributes is the Likert scale.
The Likert scale is a popular method for measuring attitudes, opinions, and perceptions of individuals towards a particular attribute or construct.
It consists of a series of statements or items that respondents are asked to rate on a scale typically ranging from "Strongly Disagree" to "Strongly Agree" or from "Very Unsatisfied" to "Very Satisfied."
The scale can vary in the number of response options, but it usually has five or seven points.
The Likert scale provides a way to quantify subjective responses and allows researchers to gather data on people's preferences, opinions, and perceptions.
It is widely used in various fields such as psychology, social sciences, market research, and customer satisfaction surveys.
Therefore, the Likert scale is the most widely used method for rating attributes.
To learn more about Likert scale go to:
https://brainly.com/question/29673854
#SPJ11
1. Find the value of the expressions using the correct order of operations.
a. -8 +5 (-3))
b. 5. (
29)
- 8+ -15 = -23
c. -57-4-3
0
d. 4+ (-5). 5-6
e. 3.-5. (-5)
f. (-5 + 4) 8
-8
21
8.
P: -64.-16 -
2
-5
i. -8
4
2. Find the value of the expressions when x = -2 and y - 5.
a. x(y + 1) -2 (5+1)
b. xy + 1
c. -2(x + y)

Answers

create a video explaning the solution of this problem.
help me create a script and the answer for the problem thank you!

Answers
The grounded ends of the guy wires are 15 meters apart.
How to calculate tie valueUsing the Pythagorean theorem, we can calculate the length of the base (distance between the grounded ends of the guy wires).
Let's denote the length of the base as 'x.'
According to the problem, the height of the tower is 20 meters, and the length of each guy wire is 25 meters. Thus, we have a right triangle where the vertical leg is 20 meters and the hypotenuse is 25 meters.
Applying the Pythagorean theorem:
x² + 20² = 25²
x² + 400 = 625
x² = 225
x = √225
x = 15
Therefore, the grounded ends of the guy wires are 15 meters apart.
Learn more about Pythagorean theorem on
https://brainly.com/question/343682
#SPJ1
A gas supplier maintains a team of engineers who are available to deal with leaks reported by customers. Most reported leaks can be dealt with quickly, but some require a long time. The time taken to deal with reported leaks is found to have a mean of 65 minutes and a standard deviation of 60 minutes. Assuming that the times may be modeled by a normal distribution, estimate the probability that it will take between 30 minutes and 60 minutes to deal with a reported leak.
Answers
The probability that it will take between 30 and 60 minutes to deal with a reported leak is approximately 0.187.
Mean time, μ = 65 minutes
Standard deviation, σ = 60 minutes
Probability that it will take between 30 and 60 minutes to deal with a reported leak.
The probability of dealing with a leak in a particular range can be found using the standard normal distribution.The standard normal distribution has a mean of 0 and a standard deviation of 1.
The formula for converting a normal distribution to a standard normal distribution is:
z = (x - μ)/σ
where x is the observed value
.We need to find the z-scores for the given values.
z1 = (30 - 65)/60 = -0.5833z2 = (60 - 65)/60 = -0.0833
Now we need to find the area between these two z-scores using a standard normal distribution table or calculator.
P(z1 < Z < z2) = P(-0.5833 < Z < -0.0833) = P(Z < -0.0833) - P(Z < -0.5833) = 0.4664 - 0.2794 = 0.187
Learn more about probability at
https://brainly.com/question/31260142
#SPJ11