Select all the ratios that are equivalent to the ratio 12 : 3.
Multiple select question.
cross out
A)
6 : 1
cross out
B)
1 : 4
cross out
C)
4 : 1
cross out
D)
24 : 6
cross out
E)
15 : 6
cross out
F)
1,200 : 300
cross out
G)
112 : 13

Answers
Answer:
i am pretty sure it is c d and f
Step-by-step explanation:
12:3=4:1 because you divide both by 3
12:3=24:6 because you multiply by 2 for each
12:3=1200:300 because you multiply by 100
Related Questions
A scale model of the U.S. National Monument is 10 inches tall. The actual monument is 100 feet tall. Write a scale using the same units on both sides. Example: 1cm = 100cm. (remember, there are 12 inches in 1 foot)
Answers
Answer:
The height of the scale model is 10 inches, and the height of the actual monument is 100 feet. Since there are 12 inches in 1 foot, we can convert the height of the actual monument to inches:
100 feet × 12 inches/foot = 1200 inches
Now we can write the scale as:
1 inch : 120 feet
This means that one inch on the scale model represents 120 feet of the actual monument.
please help me i will give brainliest to first person to anwser.

Answers
First we start with the formula for cylinders v=(pi)r(squared)h filled in Thats v=(3.14)(8 squared) (8) which brings us to the answer 1607.68 but you must round to the nearest tenth aka 1607.7

Answer:
The first option, V ≈ 1607.7 in²
Step-by-step explanation:
Find the volume of the given cylinder.
\(\begin{center}\framebox{\parbox{4cm}{\textbf{Volume of a Cylinder:}\\[2ex]The volume of a cylinder with radius $r$ and height $h$ is given by the formula:\\[2ex]\center{$V = \pi r^2 h$} \\ \\}}\end{center}\)
Given:
r = 8 in
h = 8 in
π = 3.14
Find:
V = ?? in³
\(\hrulefill\)
Now solving,
Substitute the given values into the formula:
=> V = (3.14)(8)²(8)
Using a calculator to simplify:
=> V = 1607.68 in²
Rounded to the nearest tenth:
∴ V ≈ 1607.7 in²
Thus, the first option is correct.
Which figure has exactly one line of symmetry? A rhombus, pentagon, rectangle and triangle are shown. A. Rhombus B. Pentagon C. Rectangle D. Triangle
Answers
Answer: The figure that has exactly one line of symmetry is B. Pentagon.
Step-by-step explanation: A line of symmetry is a line that divides a figure into two congruent halves that are mirror images of each other. A figure can have zero, one, or more lines of symmetry depending on its shape and orientation. To find the lines of symmetry of a figure, we can use a paper folding method or a reflection test. A paper folding method involves folding the figure along a line and checking if the two halves match up exactly. A reflection test involves reflecting the figure over a line and checking if the image coincides with the original figure.
Using either method, we can see that:
A. Rhombus has two lines of symmetry: one diagonal and one vertical.
C. Rectangle has two lines of symmetry: one horizontal and one vertical.
D. Triangle has either zero or three lines of symmetry depending on the type of triangle. An equilateral triangle has three lines of symmetry: one vertical and two bisecting the angles. An isosceles triangle has one line of symmetry: the perpendicular bisector of the base. A scalene triangle has no lines of symmetry.
B. Pentagon has either zero or five lines of symmetry depending on the type of pentagon. A regular pentagon has five lines of symmetry: each passing through a vertex and the midpoint of the opposite side. An irregular pentagon has no lines of symmetry.
Therefore, the only figure that has exactly one line of symmetry is B. Pentagon, but only if it is an isosceles pentagon.
Hope this helps, and have a great day! =)
5 + n2 > 8
A. n > 6
B. n>3
C. n>1.5
D. n < 26
Answers
then dive both sides 2n>8
and get n>4
Answer: n>1.5
( n2 here means 2×n not n² )
Step-by-step explanation:
5 + 2n > 8
Subtract 5 from both sides
5 -5 + 2n > 8 -5
2n > 3. Divide both sides by 2
2n/2 > 3/2
n = 1.5
Please Help!!!!!What is the area of the polygon below?

Answers
Answer:
48 mm squared
Step-by-step explanation:
divide the shape into 3 parts- left square, middle joining rectangle, and right rectangle
a) the right most square has an area of 4 by 4 ie 16 mm sq.
b) the middle adjoining rectangle and length of 2 mm and breadth of 1mm making its area 2mm sq.
c) the right rectangle has height 5 mm nad breadth 6mm making the area 30 mm sq.
adding parts a b and c the total area is 16+2+30 = 48 mm squared
Answer:
48 square mm
Step-by-step explanation:
see attached image
We have 3 rectangles now.
16+2+30
=48
So, the area is 48 square mm.
Hope this helps! :)

Pls and thank you. will get brainiest IF the answer it accurate :p
What is the simplified expression for the expression below? 4(x + 8) + 5(x – 3)
1.) 9x + 5
2.) 9x + 11
3.) 9x + 17
4.) 9x + 47
Answers
4x+5x is 96 4*8 is 32 5*-3 is -15 32+-15 is 17
More Math about Slope
thx
(for questions 3 and 4, i know that one of them is 0 and the other is unidentified, but i don't know which one is which)
(and the 5th screenshot has the answer choices if needed)
happy easter-eve





Answers
Answer: 3 is 0 and 4 is unidentified
Step-by-step explanation:
The horizontal line has a slope of zero, think of it as you can walk on it or not. Since four has all X's as eight that creates a vertical slope which cannot be walked on.
Thanks for the opportunity to help you! :)
1. m/slope=6/1 or 6. Use the first two points for the formula y₂-y₁/x₂-x₁. B
2.m=-4 or -12/3. Use the slope formula and substitute the points. G
3. m=zero. I
4.m=undefined. A

how do I know if im diving with ratio's or multiplying? please put a equation problem about dividing and multiplying ratios
Answers
Answer:
3/4 x 2/5
6/9 ÷ 4/7
Step-by-step explanation:
Use the Midpoint Rule with \(n=5\) to estimate the volume obtained by rotating about the y-axis the region under the curve \(y=\sqrt{1+x^3}\), \(0\leq x\leq 1\).
Answers
To estimate the volume using the Midpoint Rule with \(\displaystyle n=5\), we need to divide the interval \(\displaystyle 0\leq x\leq 1\) into \(\displaystyle n\) subintervals of equal width. Since \(\displaystyle n=5\), each subinterval will have a width of \(\displaystyle \Delta x=\frac{1-0}{5}=\frac{1}{5}\).
Now, let's calculate the volume using the Midpoint Rule. The formula for the volume obtained by rotating about the y-axis is:
\(\displaystyle V\approx 2\pi \sum _{i=1}^{n}y_{i}\Delta x\)
where \(\displaystyle y_{i}\) represents the value of the function \(\displaystyle y=\sqrt{1+x^{3}}\) evaluated at the midpoint of each subinterval.
First, let's find the midpoints of the subintervals. Since the width of each subinterval is \(\displaystyle \Delta x=\frac{1}{5}\), the midpoint of the \(\displaystyle i\)-th subinterval is given by:
\(\displaystyle x_{i}=\frac{\Delta x}{2}+\left( i-\frac{1}{2}\right) \Delta x=\frac{1}{10}+\left( i-\frac{1}{2}\right) \frac{1}{5}\)
Substituting \(\displaystyle x_{i}\) into the function \(\displaystyle y=\sqrt{1+x^{3}}\), we obtain:
\(\displaystyle y_{i}=\sqrt{1+\left( \frac{1}{10}+\left( i-\frac{1}{2}\right) \frac{1}{5}\right) ^{3}}\)
Now, we can calculate the approximate volume using the Midpoint Rule:
\(\displaystyle V\approx 2\pi \sum _{i=1}^{5}y_{i}\Delta x\)
Substituting the values of \(\displaystyle y_{i}\) and \(\displaystyle \Delta x\) into the formula, we can evaluate the sum and compute the estimated volume.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
The stem-and-leaf plot displays data collected on the size of 15 classes at two different schools.
Mountain View School Seaside School
0 5, 8
9, 8, 2, 0 1 0, 1, 2, 5, 6, 8
8, 7, 6, 5, 5, 4, 4, 3, 1, 0 2 5, 5, 7, 7, 8
0 3 0, 6
Key: 2 | 1 | 0 means 12 for Mountain View and 10 for Seaside
Part A: Calculate the measures of center. Show all work. (2 points)
Part B: Calculate the measures of variability. Show all work. (1 point)
Part C: If you are interested in a smaller class size, which school is a better choice for you? Explain your reasoning. (1 point)
Answers
For Mountain View School:
Data: 0, 0, 0, 0, 1, 2, 3, 4, 4, 5, 5, 5, 5, 6, 7, 8, 8, 8, 9
Mean: (0 + 0 + 0 + 0 + 1 + 2 + 3 + 4 + 4 + 5 + 5 + 5 + 5 + 6 + 7 + 8 + 8 + 8 + 9) / 19
= 100 / 19
≈ 5.26
To find the median, we need to arrange the data in ascending order: 0, 0, 0, 0, 1, 2, 3, 4, 4, 5, 5, 5, 5, 6, 7, 8, 8, 8, 9.
The median is the middle value, which is the 10th value in this case.
Median: 5
For Seaside School:
Data: 0, 0, 0, 1, 1, 2, 2, 4, 5, 5, 5, 5, 6, 7, 7, 8, 8, 8, 9
Mean: (0 + 0 + 0 + 1 + 1 + 2 + 2 + 4 + 5 + 5 + 5 + 5 + 6 + 7 + 7 + 8 + 8 + 8 + 9) / 19
= 80 / 19
≈ 4.21
To find the median, we need to arrange the data in ascending order: 0, 0, 0, 1, 1, 2, 2, 4, 5, 5, 5, 5, 6, 7, 7, 8, 8, 8, 9.
The median is the middle value, which is the 10th value in this case.
Median: 5
Now let's calculate the measures of variability, specifically the range and interquartile range (IQR).
Range: The range is the difference between the largest and smallest values in the dataset.
For Mountain View School:
Range: 9 - 0 = 9
For Seaside School:
Range: 9 - 0 = 9
Interquartile Range (IQR): The IQR is the difference between the third quartile (Q3) and the first quartile (Q1) and measures the spread of the middle 50% of the data.
For Mountain View School:
Q1 = 3
Q3 = 7
IQR = Q3 - Q1 = 7 - 3 = 4
For Seaside School:
Q1 = 2
Q3 = 7
IQR = Q3 - Q1 = 7 - 2 = 5
To determine which school is a better choice for a smaller class size, we can consider both the mean and the median.
Both the mean and median for Mountain View School are higher than those for Seaside School. This suggests that, on average, the class sizes at Mountain View School are larger than those at Seaside School. Therefore, if you are interested in a smaller class size, Seaside School would be a better choice
For Mountain View School:
- Median: The median class size is the middle value, which is 25.
- Mean: The mean class size is the sum of all the class sizes divided by the total number of classes, which is (29 + 28 + 28 + 27 + 25 + 24 + 24 + 23 + 21 + 20 + 19 + 18 + 15 + 13 + 10) / 15 = 21.27.
For Seaside School:
- Median: The median class size is the middle value, which is 20.
- Mean: The mean class size is the sum of all the class sizes divided by the total number of classes, which is (25 + 25 + 27 + 27 + 28 + 28 + 28 + 30 + 31 + 35 + 36 + 38 + 40 + 43 + 45) / 15 = 31.13.
Part B:
For Mountain View School:
- Range: The range is the difference between the largest and smallest values, which is 29 - 10 = 19.
- Interquartile Range (IQR): The IQR is the difference between the third quartile (Q3) and the first quartile (Q1). From the stem-and-leaf plot, we can see that Q1 is 20 and Q3 is 28. Therefore, the IQR is 28 - 20 = 8.
For Seaside School:
- Range: The range is the difference between the largest and smallest values, which is 45 - 25 = 20.
- Interquartile Range (IQR): The IQR is the difference between the third quartile (Q3) and the first quartile (Q1). From the stem-and-leaf plot, we can see that Q1 is 27 and Q3 is 38. Therefore, the IQR is 38 - 27 = 11.
Part C:
If you are interested in a smaller class size, Mountain View School is a better choice for you because it has a lower mean and median class size than Seaside School.
Total students= 27; girls:total students = 2:3. How many boys and girls are there?
Answers
Answer:
18 girls and 9 boys
Answer:
Step-by-step explanation:
2:3 ?:27
How does 3 get to 27? x9. 2 x 9? 18
2:3 18:27
Information: 18 girls and 27 students.
The others must be boys. 27 - 18 = 9
There are 9 boys and 18 girls. Ratio: 9 to 18 or 9:18 or 9/18 You can simplify to 1 boy for every 2 girls. Ratio: 1 to 2 or 1:2 or 1/2
Solve for y.
−2y+7=−5
Responses
y = 6
y = 1
y = -1
y = -6
Answers
Answer: y = 6
Step-by-step explanation:
1. Subtract 7 from both sides to isolate -2y.
-2y = -12
2. Divide both sides by -2 to isolate the y.
y = 6

Which of the following lines of best fit could correspond to a data set with a correlation coefficient of −0.9?
A. y=3x−0.9 B. y=0.9x+3 C. y=−2x−6 D. y=−0.9

Answers
Answer:
D
Step-by-step explanation:
Dddddddddddddddddddddddddddddd
A fruit juice recipe calls for 2 parts orange juice and 8 parts pineapple juice. Which proportion can be used to find the amount of orange juice, j, that is needed to add to 18 L of pineapple juice?
2 over 8 equals j over 18
8 over 2 equals j over 18
8 over j equals 2 over 18
16 over 18 equals j over 100
Answers
The correct proportion to use to find the amount of orange juice, j, needed to add to 18 L of pineapple juice is:
2/8 = j/18
This proportion relates the ratio of orange juice to pineapple juice in the recipe (2:8) to the amount of orange juice needed to add to 18 L of pineapple juice. By cross-multiplying, we can solve for j as follows:
2/8 = j/18
218 = 8j
36 = 8*j
j = 36/8
j = 4.5
Therefore, you would need to add 4.5 L of orange juice to 18 L of pineapple juice to create the fruit juice recipe that calls for a ratio of 2 parts orange juice to 8 parts pineapple juice.
Answer:
2 over 8 equals j over 18Step-by-step explanation
2 over 8 equals j over 18
This proportion represents the ratio of orange juice to pineapple juice in the recipe. By setting up the proportion, we can solve for the value of 'j,' which represents the amount of orange juice needed.
So, the correct proportion is:
2 over 8 equals j over 18
I=PRT
Courtney borrowed $7,500 for 4 years at an annual interest rate of 8%.
Part A: How much interest will she pay on the loan?
Part B: What is the total balance after the 4 years?
Answers
Part A: $2,400
Part B: $9,900
First, you need to find how much interest she is paying annually by taking the 8% and finding out what is 8% of $7,500. To do this, we can set two fractions up side by side, x/7,500 and 8/100. The denominators mean 100% of 7,500 is 7,500. The numerators mean that x is 8% of 7,500.
So to find x, we can cross multiply 7,500 and 8, giving us 60,000. Then we can divide 60,000 by 100, to give us 600. So x=600. 600 is how much interest costs for 1 year.
Now, to find how much interest is for 4 years, all we have to do is multiply 600 by 4. This gives us 2400. So, 4 years of interest costs her $2,400.
Her total balance after the 4 years is just the 4 year interest plus the amount borrowed. So 2,400 + 7,500. Giving us $9,900.
Can someone help me? lol..

Answers
-3x - 5x - 6
simplifies to...
Answers
-8x - 6
Hope this helps! Please comment if I am right or not.
Answer:-8x-6
Step-by-step explanation:-3x-5x-6,(-3-5)x-6, solution -8x-6.
Can someone please help?

Answers
answers are in the picture
goodluck :)

Since the base of both numbers are the same, keep the base. In this case, it’s 2. Next add the exponents together. 3 + 2 = 5.
So the simplified one would be 2^5 (two to the fifth power)
2. Multiply 2 by itself five times; 2 • 2 • 2 • 2 • 2 = 64
So evaluated (calculated) the answer would be 64.
Hi! I don't really get what or how to solve this question.
Which of the following sets of measurements cannot represent the three side lengths of a triangle?
A. 5cm, 5cm, 5cm
B. 5cm, 6cm, 7cm
C. 5cm, 7cm, 12cm
D. 5cm, 10cm, 11cm
Answers
Answer:
C and D
Step-by-step explanation:
you could draw them connecting to each other using your ruler and predict if ita a triangle or not .
also the sum of any 2 sides of a triangle must be greater than the measure of the third side unless equilateral Triangle
can someone help me out? :P

Answers
9514 1404 393
Answer:
181
Step-by-step explanation:
The tagged deer seem to represent about 17/110 of the population. Since there are 28 deer with tags, the population (p) is estimated to be ...
110/17 = p/28
p = 28(110/17) ≈ 181
There are about 181 deer in the woods.
Julia the teacher has 7.03 hours to teach her class. She has a red folder and a blue folder. In the red folder is a lesson about Egypt that will take 5 hours. In the blue folder is a lesson about coding that will take 3.0 hours. Which lesson should she choose?
Answers
the ratio of the number of oranges to apples to bananas is 8:5:2. if there are 120 fruits in total, how many bananas are there
Answers
Answer:
Step-by-step explanation:
To find the number of bananas, we need to determine the proportion of bananas in the total number of fruits based on the given ratio.
Let's assume that the ratio of oranges, apples, and bananas can be represented by 8x, 5x, and 2x, respectively, where x is a common multiplier.
The sum of the parts in the ratio is 8x + 5x + 2x = 15x.
We know that the total number of fruits is 120. Therefore, we can set up the following equation:
15x = 120
To solve for x, we divide both sides of the equation by 15:
x = 120 / 15
x = 8
Now that we know the value of x, we can find the number of bananas by multiplying it by the corresponding part of the ratio:
Number of bananas = 2x = 2 * 8 = 16
So, there are 16 bananas in total.
We can add all the parts to the ratio and get 15. Out of 15 parts, 2 are bananas. Now we can calculate how many fruits are in one part. One fifteenth of 120 is 8, so there are 8 fruits in one part. 2 parts are bananas, so multiplying 8 with 2 gives us our answer, 16.
y= -3/2x + 5 for x= 0,2,4 (3/2 is a fraction)
Answers
Answer:
y= 5, 17/4 , 37/8 must be the answers.
Some students recorded how many minutes they spent on the phone in one day. They put the results in a Stem-and-Leaf Plot.
What is the mean number of minutes spent on the phone?

Answers
Explanation:
The data from the stem-and-leaf plot is:
10,
24,25,26,
30,30,32,33,
40,45,46
Add up those values
10+24+25+26+30+30+32+33+40+45+46 = 341
Then divide over n = 11 which is the sample size.
341/11 = 31 is the arithmetic mean.
Answer:
341/11 = 31 is the arithmetic mean.
Step-by-step explanation:
2,000,000 ÷ 152 x 12 - 10,000 = ?

Answers
Answer:
147894.736842
Maths Equations if you solve it right I will give you the brainiest! Don't solve it only for points bc I will report you! if you can't solve it just leave it for someone who can.

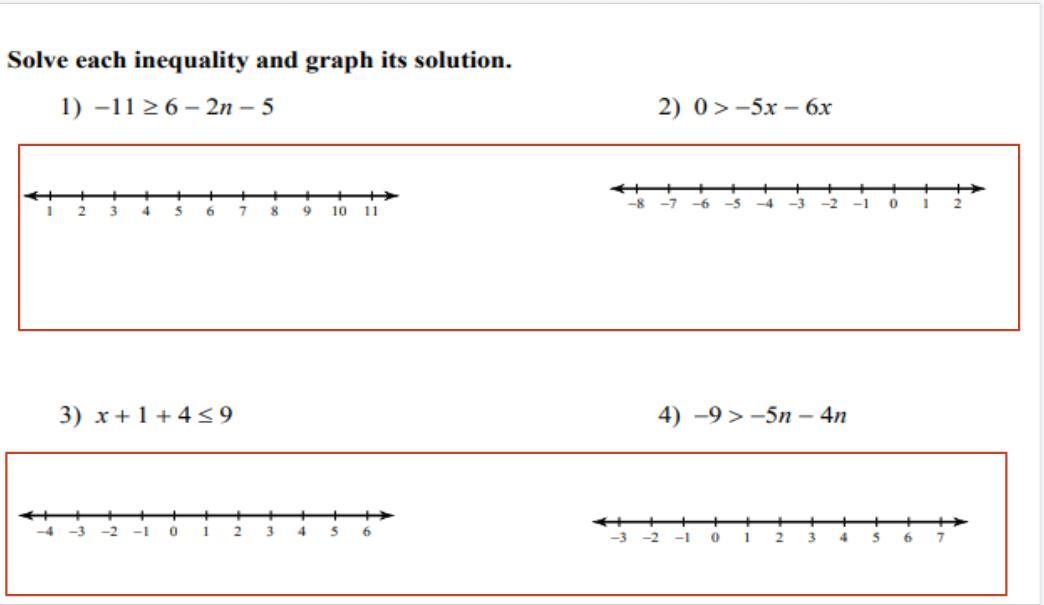
Answers
2. 1 is greater than x
3. X is less than or equal to 4
4. 1 is greater than n
5. K is greater than 3
6. -3 is greater than or equal to p
7. -1 is less than a
8. 8 is less an or equal to x
I hope this helps!
An image of a rhombus is shown.
A rhombus with a base of 17 inches and a height of 14 inches.
What is the area of the rhombus?
62 in2
119 in2
124 in2
238 in2

Answers
Answer:
238 in.²
Step-by-step explanation:
For a parallelogram, A = bh.
A = bh
A = 17 in. × 14 in.
A = 238 in.²
Write 7^3 x 7^2 using a singular exponent.
Answers
Answer:
7^5
Step-by-step explanation:
The base number (7) is the same, so we can just add the exponents together.
Hope that helped!
To write 7^3 x 7^2 using a singular exponent, you can add the exponents together since the bases (7) are the same. The result is:
7^3 x 7^2 = 7^(3 + 2) = 7^5\(\huge{\mathcal{\colorbox{black}{\textcolor{lime}{\textsf{I hope this helps !}}}}}\)
♥️ \(\large{\textcolor{red}{\underline{\texttt{SUMIT ROY (:}}}}\)
repost: Каков объем этой прямоугольной призмы?
45 кубических дюймов
81 кубический дюйм
180 кубических дюймов
405 кубических дюймов
(english: What is the volume of this rectangular prism?
45 cubic inches
81 cubic inches
180 cubic inches
405 cubic inches

Answers
So first of all we should know that the rectangular prism is a cuboid.
\( \\ \\ \)
Given :-heigth = 9 in.Length = 5 in.Width = 4 in.\( \\ \)
To find:-Volume of cuboid.\( \\ \)
Solution:-We know:-
\( \bigstar \boxed{ \rm volume \: of \: cuboid = length \times width \times height}\)
\( \\ \\ \)
So:-
\( \dashrightarrow \sf volume \: of \: cuboid = length \times width \times height \\ \)
\( \\ \\ \)
\( \dashrightarrow \sf volume \: of \: cuboid = 9 \times 5 \times 4 \\ \)
\( \\ \\ \)
\( \dashrightarrow \sf volume \: of \: cuboid = 45 \times 4 \\ \)
\( \\ \\ \)
\( \dashrightarrow \bf volume \: of \: cuboid = 180 {in}^{3} \\ \)
Therefore option C is correct .
\( \\ \\ \)
know more:-\( \\ \\ \)
\(\begin{gathered}\begin{gathered}\: \: \: \: \: \: \begin{gathered}\begin{gathered} \footnotesize{\boxed{ \begin{array}{cc} \small\underline{\frak{\pmb{ \red{More \: Formulae}}}} \\ \\ \bigstar \: \bf{CSA_{(cylinder)} = 2\pi \: rh}\\ \\ \bigstar \: \bf{Volume_{(cylinder)} = \pi {r}^{2} h}\\ \\ \bigstar \: \bf{TSA_{(cylinder)} = 2\pi \: r(r + h)}\\ \\ \bigstar \: \bf{CSA_{(cone)} = \pi \: r \: l}\\ \\ \bigstar \: \bf{TSA_{(cone)} = \pi \: r \: (l + r)}\\ \\ \bigstar \: \bf{Volume_{(sphere)} = \dfrac{4}{3}\pi {r}^{3} }\\ \\ \bigstar \: \bf{Volume_{(cube)} = {(side)}^{3} }\\ \\ \bigstar \: \bf{CSA_{(cube)} = 4 {(side)}^{2} }\\ \\ \bigstar \: \bf{TSA_{(cube)} = 6 {(side)}^{2} }\\ \\ \bigstar \: \bf{Volume_{(cuboid)} = lbh}\\ \\ \bigstar \: \bf{CSA_{(cuboid)} = 2(l + b)h}\\ \\ \bigstar \: \bf{TSA_{(cuboid)} = 2(lb +bh+hl )}\\ \: \end{array} }}\end{gathered}\end{gathered}\end{gathered}\end{gathered}\)
I need help ASP!!! LAST QUESTION!!!

Answers
Explanation: 4/8 + 3/8 = 7/16