Select the correct answer from each drop-down menu. Consider the function f(x) = 3x + 1 and the graph of the function g(x) shown below. A coordinate plane linear graph function shows a line intersecting Y-axis at minus 5 and X-axis at 1.5. The graph g(x) is the graph of f(x) translated units , and g(x) = .
Answers
The graph g(x) is the graph of f(x) translated 6 units right, and g(x) = 3x - 5
How to determine the translation?The function f(x) is given as:
f(x) = 3x + 1
Next, we calculate the equation of g(x) using:
\(g(x) = \frac{y_2 -y_1}{x_2 -x_1} * (x - x_1) + y_1\)
Where:
(x1,y1) = (0,-5) and (x2,y2) = (1.5,0)
So, we have:
\(g(x) = \frac{0+5}{1.5 -0} * (x - 0) -5\)
Evaluate
g(x) = 3x -5
So, we have:
f(x) = 3x + 1
g(x) = 3x -5
Subtract f(x) from g(x) to calculate the units of translation (k)
k = 3x - 5 - 3x - 1
k = -6
This means
k = 6 units right
Hence, the graph g(x) is the graph of f(x) translated 6 units right, and g(x) = 3x - 5
Read more about translation at:
https://brainly.com/question/17067858
#SPJ1

Related Questions
Use Evcel fo find the probabinty that in 112 trials with probabinty
0.42
of success that there are 30 or fewer suce ses. Round to 6 decimaiplaces Type your answer hern
Answers
Answer:
0.5
Step-by-step explanation:
0.5=0.42 then the answer is 0.5
binomial expanion of (1 i)^2n 2^ncos(npi/2)
Answers
The binomial expansion of (1 + i)^2n can be written as ∑(n choose k)(i^k)(1^(n-k)), where (n choose k) represents the binomial coefficient of n and k. And that's the binomial expansion of (1+i)^2n * 2^n * cos(nπ/2).
Using the identity cos(npi/2) = 0 when n is odd and cos(npi/2) = (-1)^n/2 when n is even, we can simplify the expression to:
(1 + i)^2n * 2^n * cos(npi/2) = ∑(n choose k)(i^k)(1^(n-k)) * 2^n * cos(npi/2)
When n is odd, cos(npi/2) = 0, so the expression simplifies to:
∑(n choose 2k)(i^(2k))(1^(n-2k)) * 2^n
When n is even, cos(npi/2) = (-1)^n/2, so the expression simplifies to:
∑(n choose 2k)(i^(2k))(1^(n-2k)) * 2^n * (-1)^(n/2)
Therefore, the binomial expansion of (1 + i)^2n * 2^n * cos(npi/2) can be written as either of these simplified forms, depending on whether n is odd or even.
The binomial expansion of (1+i)^2n * 2^n * cos(nπ/2).
Step 1: Apply the binomial theorem to the term (1+i)^2n.
The binomial theorem states that (a+b)^n = Σ [n! / (k!(n-k)!) * a^k * b^(n-k)], where the sum runs from k=0 to k=n.
In this case, a=1 and b=i. Applying the theorem:
(1+i)^2n = Σ [2n! / (k!(2n-k)!) * 1^k * i^(2n-k)]
Step 2: Simplify the expression for the binomial expansion.
For the complex number i, we have i^2 = -1, i^3 = -i, and i^4 = 1. Using this pattern, we can rewrite the i^(2n-k) term in the expansion:
(1+i)^2n = Σ [2n! / (k!(2n-k)!) * 1^k * (-1)^((2n-k)/2) * i^(k % 4)], for even k values.
Step 3: Multiply the binomial expansion by 2^n * cos(nπ/2).
Now, we just need to multiply our expansion by the given factors:
(1+i)^2n * 2^n * cos(nπ/2) = Σ [2n! / (k!(2n-k)!) * 1^k * (-1)^((2n-k)/2) * i^(k % 4) * 2^n * cos(nπ/2)], for even k values.
And that's the binomial expansion of (1+i)^2n * 2^n * cos(nπ/2).
Visit here to learn more about binomial expansion:
brainly.com/question/29260188
#SPJ11
choose the graph that represents the linear equation y = 2x + 1

Answers
Answer:
The third option is the answer.
Step-by-step explanation:
In the formula y = mx + b, using the equation given,
m = 2, which means that the line goes up 2 units and right 1 unit.b = 1, which means that the y-intercept, or where the line touches the y-axis, is 1.Answer:
the 3rd option
Step-by-step explanation:
In the formula y = tx + b, using the equation given,
t = 2, which means that the line goes up 2 units and right 1 unit.
b = 1, which means that the y-intercept, or where the line touches the y-axis, is 1.
Kerim jogged 3 miles on Thursday: On Friday, he jogged of a mile
farther. How far did he jog on Friday
Answers
Answer:
4 miles
Step-by-step explanation:
3 miles plus 1 additional mile is 4 miles.
Compute i to the 93 power In algebra 2
Answers
i^93 = i^92 x i
i^92 =(i^2)^46
Now you have i(i^2)^46
i^2 = -1
Now you have i(-1)^46
-1^46 = 1
Now you have 1i which = i
The answer is i
You bought a car and are financing $12,000 at 7% over 5 years. Your monthly payment is $297.02. How much of that payment represents the interest payment? $55 $70 $76 $92
Answers
The interest payment in the monthly payment of $297.02 for a financing of $12,000 at 7% over 5 years is $70. Option b is correct.
The interest payment of the given financing can be calculated by the given parameters as follows:
We are given that the amount financed is $12,000 for a period of 5 years and an annual interest rate of 7%.The monthly payment is given to be $297.02.
Compute the total interest on the loan over the 5-year period using the below formula:
Total Interest = (Amount Financed) x (Annual Interest Rate) x (Number of Years)
Total Interest = $12,000 x 7% x 5 years
Total Interest = $4,200
Compute the total number of monthly payments:
Total number of payments = Number of years x 12
Total number of payments = 5 x 12
Total number of payments = 60
Finally, calculate the interest payment component of the monthly payment using the below formula:
Interest payment = Total interest / Total number of payments
Interest payment = $4,200 / 60
Interest payment = $70
Therefore, the interest payment is $70. Option b is correct.
Learn more about interest payment https://brainly.com/question/32050786
#SPJ11
Each of these sequence or series formulas involves four quantities that are represented by a variable. For each fomula, describe the four quantities.
d. S n = a₁ (1-rⁿ ) / 1-r
Answers
The formula for finding the sum of a geometric series is:
S n = a₁ (1-rⁿ )/(1-r)
The four quantities in the formula are S n, a₁, r, n
How to describe the four quantities?An infinite geometric series is the outcome of an unlimited geometric sequence. An infinite geometric series is the outcome of an unlimited geometric sequence. This series wouldn't have a finish. It is possible to calculate the sum of all finite geometric series.
The terms in the sequence will grow steadily larger, but adding the larger numbers together will not provide a solution if the common ratio of an infinite geometric series is greater than one.
The formula for finding the sum of a geometric series is:
S n = a₁ (1-rⁿ )/(1-r)
The four quantities in the formula are S n, a₁, r, n
The description is as follows:
n be the number of terms
a₁ be the first term
r be the common ratio
\(S_n\) be the sum of a geometric series
To learn more about geometric series, refer to:
https://brainly.com/question/12383793
#SPJ4
System A
6x-y=-5
-6x+y=5
System B
x+3y=13
-x+3y=5
O The system has no solution.
The system has a unique solution:
(x, y) = (
The system has infinitely many solutions.
The system has no solution.
The system has a unique solution:
(x, y) = (
O The system has infinitely many solutions.
Answers
Answer:
Step-by-step explanation:
6x-y=-5
-6x+y=5
Adding the 2 equations we have:
0 + 0 = 0
0 = 0
This means there are infinite solutions
- the equations are identical.
System B
x+3y=13
-x+3y=5
Adding:
6y = 18
y = 3.
x = 13 - 3(3) = 4.
The system has a unique solution
(x. y) = (4, 3).
need help asap!!!! can you guys please help me on the problem ty ty ty ty ty so much!!!!!!

Answers
Answer:
It's J
Step-by-step explanation:
when has only ONE zero it'll intercept the x axis one time
A man on a 135 ft verticals cliff looks down at an angle of 16 degrees and sees his friend. How far away is the man from his friend? How far is the friend from the base of the cliff?
Answers
Answer:
a) 489.77 ft from friend
b) 470.80 ft from cliff
Step-by-step explanation:
Given a man on a 135 ft cliff sees his friend at an angle of depression of 16°, you want to know the distance of the man from his friend, and the distance of the friend from the cliff.
Trig relationsThe relevant trig relations are ...
Sin = Opposite/Hypotenuse
Tan = Opposite/Adjacent
GeometryThe 135 ft height of the cliff is modeled as the side of a right triangle that is opposite the angle of elevation from the friend to the top of the cliff. (See attachment 2.) That angle is the same as the angle of depression from the top of the cliff to the friend.
The hypotenuse of the triangle is the distance between the man and his friend. The side of the triangle adjacent to the friend is the distance to the cliff.
Using the above relations, we have ...
sin(16°) = (cliff height)/(distance to friend)
tan(16°) = (cliff height)/(distance to cliff)
Solving for the variables of interest gives ...
distance to friend = (cliff height)/sin(16°) = (135 ft)/sin(16°) ≈ 489.77 ft
distance to cliff = (cliff height)/tan(16°) = (135 ft)/tan(16°) ≈ 470.80 ft
The ma is 489.77 ft from his friend; the friend is 470.80 ft from the cliff.
__
Additional comment
The distances are given to more decimal places than necessary so you can round the answer as may be required.
<95141404393>


A ship travels due west for 83 miles . It then travels in northwest direction for 111 miles and ends up 165 miles from its original position. To the nearest tenth of a degree how many degrees north of west did it turn when it changed direction? Show your work.
Answers
*see attachment for the diagram of the information given
Answer:
115.8°
Step-by-step explanation:
Due west = 83 miles
Northwest = 111 miles
Distance to its original position = 165 miles
Let x represent the degree north of west that it turned when it changed direction which is the opposite angle of 165 miles.
Thus, to find x, we'd apply the Law of Cosine which is given as:
c² = a² + b² - 2ab*cos C
Where,
C = x
a = 83 miles
b = 111 miles
c = 165 miles
Plug in the values
165² = 83² + 111² - 2*83*111*Cos x
27,225 = 19,210 - 18,426*Cos x
27,225 - 19,210 = - 18,426*Cos x
8,015 = -18,426*Cos x
8,015 = -18,426*Cos x
8,015/-18,426 = Cos x
-0.434983176 = Cos Cmx
Cos x = -0.434983176
x = cos^{-1}(-0.434983176)
x = 115.784223°
x = 115.8°

If MJ is 25 ft. long and M'J' is 5 feet long, what was the scale factor, k?
Answers
The scale factor, if MJ is 25 ft. long and M'J' is 5 feet long is 1/5
If MJ is considered as the original figure, it is 25 ft. long.
The image of MJ, M'J' is 5 feet long
Scale factor is generally understood as the number of times the dimensions of the image is enlarged or diminished
Scale factor = Dimension of the new image ÷ Dimension of the original shape
Scale factor = M'J' length/ MJ length
k = 5/25
k = 1/5
The value of scale factor = 1/5, which means the new image is diminished.
Therefore the scale factor, if MJ is 25 ft. long and M'J' is 5 feet long is 1/5.
To learn more about scale factor refer here
https://brainly.com/question/15891755
#SPJ1
Simplify!!!!!
pls help meeee

Answers
Answer:
B. 6
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Square root propertiesStep-by-step explanation:
Step 1: Define
Identify.
\(\displaystyle \frac{3 \sqrt{20}}{\sqrt{5}}\)
Step 2: Simplify
[Square Root] Rewrite: \(\displaystyle \frac{3 \sqrt{4} \sqrt{5}}{\sqrt{5}}\)[Fraction] Reduce: \(\displaystyle 3 \sqrt{4}\)[Square Root] Evaluate: \(\displaystyle 3(2)\)[Order of Operations] Multiply: \(\displaystyle 6\)The aspect ratio of a rectangular shape is its length (L) divided by its width (W). It is expressed as L:W or L/W. If the aspect ratio of a chalkboard is 12:7 and the length is 36 in, what is the width of the chalkboard?
Answers
Answer:21
Step-by-step explanation:12 times three is 36 and 7 times 3 is 21
(pythagorean theorem and the coordinate plane mc) determine the length of the line segment shown. line segment from negative 3 comma 10 to 4 comma negative 1 13 units 12 units 7 units 3 units
Answers
Using Pythagorean Theorem, the length of the line segment from (-3, 10) to (4, -1) is 13 units.
Pythagorean theorem describes the relationship between the sides of a right triangle. It states that the square of the hypotenuse is equal to the sum of the squares of the two other side.
c² = a² + b²
Let a = vertical distance between the two points
b = horizontal distance between the two points
c = distance between the two points / length of line segment
Hence, c² = (|y₂ - y₁|)² + (|x₂ - x₁|)².
Substitute the values of x and y and solve for c.
c² = (|y₂ - y₁|)² + (|x₂ - x₁|)²
c² = (|-1 - 10|)² + (|4 - -3|)²
c² = (|-11|)² + (|7|)²
c² = 11² + 7²
c² = 121 + 49
c² = 170
c = 13.04
length of line segment ≅ 13 units
Learn more about Pythagorean theorem here: brainly.com/question/9125970
#SPJ4

A random sample of 155 observations results in 62 successes. [You may find it useful to reference the z table.]a. Construct the a 90% confidence interval for the population proportion of successes. (Round intermediate calculations to at least 4 decimal places. Round "z" value and final answers to 3 decimal places.)b. Construct the a 90% confidence interval for the population proportion of failures. (Round intermediate calculations to at least 4 decimal places. Round "z" value and final answers to 3 decimal places.)
Answers
For a random sample of 155 observations results in 62 successes.
a) A 90% confidence interval for the population proportion of successes is equals to the (0.335 , 0.465).
b) A 90% confidence interval for the population proportion of failure is equals to the (0.535 , 0.665).
We have a random sample of 155 observations results in 62 successes. So,
Observed value, x = 62
Sample size,n = 155
Population Proportion, p = x/n
= 62/155
= 0.4
a) We have to determine 90% confidence interval for the population proportion of successes. Using the distribution table, for 90% confidence interval, z-score value is equals to 1.6. Consider Confidence interval formula with proportion, CI \(= p ± z×\sqrt\frac{p(1-p)}{n}\)
substitute all known values in above formula, \(= 0.4 ± 1.64\sqrt\frac{0.4(1- 0.4)}{155}\)
= 0.4 ± 0.0645
= (0.4 - 0.0645 , 0.4 + 0.0645)
= (0.335 , 0.465)
b) Now, we have to determine a 90% confidence interval for the population proportion of failures.
Now consider, here failure observed values, x = 155 - 62
= 93
proportion, p = x/n
= 93/155 = 0.6
Consider the confidence interval formula, CI \(= p ± z×\sqrt\frac{p(1-p)}{n}\)
substitute values, \(= 0.6 ±1.64×\sqrt\frac{0.6(1-0.6)}{155}\)
= 0.6 ± 0.0645
= (0.6 - 0.0645 , 0.6 + 0.0645)
= (0.535 , 0.665)
Hence, required value is (0.535 , 0.665).
For more information about confidence interval, visit :
https://brainly.com/question/17212516
#SPJ4
A cell phone plan costs $200 to start. Then there is a $50 charge each month. Write an equation relating the cost, y, and then number of months, x.
Answers
Answer:
y = 200 + 50x
Step-by-step explanation:
y = cost
x = number of months
The cost is equal to the cost to open the plan plus the monthly fee times the number of months
y = 200 + 50x
Answer:
y = 200 + 50x
Step-by-step explanation:
the cost = the base cost plus the monthly charge ($50 per the number of months you pay it)
hope this helps (/o.o)/<3
The point (-1, 3) is the turning point of the graph with equation y = x2 + ax + b,
where a and b are integers.
Find the values of a and b.

Answers
Answer:
a = 2, b = 4
Step-by-step explanation:
The equation of a parabola in standard form is
y = a(x - h)² + k
where (h, k) are the coordinates of the vertex and a is the coefficient of the x² term.
Here (h, k ) = (- 1, 3 ) and coefficient of x² term = 1 , then
y = (x - (- 1))² + 3 , that is
y = (x + 1)² + 3 ← expand factor using FOIL
y = x² + 2x + 1 + 3
y = x² + 2x + 4 ← in standard form
compare to y = x² + ax + b
with a = 2 and b = 4
The values of a and b are a = 1 and b = 3.
How did we get the values?To find the values of a and b, we can use the fact that the turning point of a quadratic function in the form y = ax² + bx + c is given by the vertex (-b/2a, f(-b/2a)).
In this case, the turning point is (-1, 3), which gives us the following equations:
\(-\frac{b}{2a} = -1 (equation 1) \\f(-\frac{b}{2a}) = 3 (equation 2)\)
Plugging equation 1 into equation 2:
f(-1) = 3
Substituting -1 into x² + ax + b:
1 - a + b = 3
Simplifying:
b - a = 2 (equation 3)
Since a and b are integers, we can try different combinations of integers that satisfy equation 3. One such pair is a = 1 and b = 3:
b - a = 3 - 1 = 2
So, the values of a and b are a = 1 and b = 3.
learn more about integers: https://brainly.com/question/929808
#SPJ3
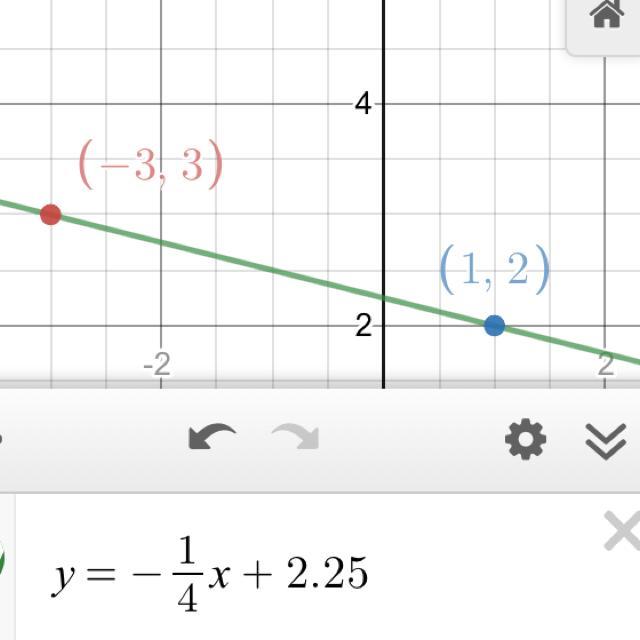
Write the equation of the line that passes through the points (-3, 3) and (1, 2).
Answers
Slope: -1/4
Y-intercept: 2.25
as the spacing between joists increases, the maximum span for any board size: A. increases only. B. decreases only. C. increases and then decreases. D. decreases and than increases
Answers
As the spacing between joists increases, the maximum span for any board size will B. decrease only. This is because the wider the spacing between joists, the more weight and pressure will be placed on the boards that are spanning the gap between them.
This means that the boards will need to be stronger in order to support the weight without bending or breaking.
If the boards are not strong enough, they may sag or bow under the weight, which can create safety hazards or damage to the structure. Therefore, it is important to use the appropriate board size and spacing between joists for any given application in order to ensure structural integrity and safety.
In summary, increasing the spacing between joists will result in a decrease in the maximum span for any board size, as the boards will need to be stronger in order to support the weight and pressure. It is important to choose the right board size and joist spacing to maintain the structural integrity and safety of the building or structure.
To learn more about joists, refer:-
https://brainly.com/question/1927626
#SPJ11
The functions f(x), g(x), and h(x) are shown below. Select the option that
represents the ordering of the functions according to their average rates of change on
the interval 1
HELP!!!
Answers
Arrange the functions according to the average rate of change in the interval 1<1. ×< 3 is: g(x) < f(x) = h(x)
In other words, g(x) has the smallest average rate of change, while f(x) and h(x) have the same largest average rate of change.
What is function?A function is a mathematical rule that takes an input (or inputs) and produces a corresponding output.
It describes a relationship between two quantities, where each input is associated with exactly one output.
Since the interval of interest is not provided, I will assume that the interval is 1 < x < 3, based on the graphs of the functions given.
To determine the ordering of the functions according to their average rates of change on the interval 1 < x < 3, we can use the following formula:
Average rate of change = (f(b) - f(a)) / (b - a)
where a and b are the endpoints of the interval.
Using this formula, we can calculate the average rates of change of the three functions on the interval 1 < x < 3. Here are the results:
f(x): average rate of change = (f(3) - f(1)) / (3 - 1) = (2 - (-2)) / 2 = 2
g(x): average rate of change = (g(3) - g(1)) / (3 - 1) = (-3 - (-1)) / 2 = -1
h(x): average rate of change = (h(3) - h(1)) / (3 - 1) = (0 - (-4)) / 2 = 2
To know more about average rates visit:
https://brainly.com/question/31182129
#SPJ1
The complete question is given below:

Arrange the functions in the period 1 according to the average rate of change. 3 is: g(x) f(x) = h(x)
In other words, g(x) has the lowest average rate of change, whereas f(x) and h(x) both have the highest average rate of change.
What is a Function?A function is a mathematical rule that accepts an input (or inputs) and generates an output.
It defines a relationship among two quantities in which each input corresponds to only one output.
Because the interval of interest is not specified, I will assume that it is 1 x 3 based on the graphs of the functions supplied.
We can use the formula that follows to find the ordering of the functions based on their average frequencies of change on the interval 1 x 3:
Change at an Average Rate = (f(b) - f(a)) / (b - a)
where a and b are the interval's ends.
We can compute the average rates of change of all three functions on the interval 1 x 3 using this formula. Here are the outcomes:
f(x): average rate of change = (f(3) - f(1)) / (3 - 1)
= (2 - (-2)) / 2
= 2
g(x): average rate of change = (g(3) - g(1)) / (3 - 1)
= (-3 - (-1)) / 2
= -1
h(x): average rate of change = (h(3) - h(1)) / (3 - 1)
= (0 - (-4)) / 2
= 2
To know more about functions, visit:
https://brainly.com/question/11624077
#SPJ1

8) Find each of the following:
a) The fifth term in the expansion of (1 + 4x)^7
b) The sixth term in the expansion of (2 - x)^11
c) The seventh term in the expansion of (3 - 2/3x)^12
9) Obtain the expansion of 2/(1-3x^2) up to the term in x^8
Answers
8 a) The fifth term in the expansion is 8,960.
b) The sixth term in the expansion is -11,264.
c) The seventh term in the expansion is approximately 28.6152.
9) The expansion of 2/(1-3x^2) up to the term in x^8 is 2 + 24x^2 + 162x^4 + 972x^6 + 1458x^8.
8) a) To find the fifth term in the expansion of (1 + 4x)^7, we use the binomial theorem formula:
(1 + 4x)^7 = C(7,0) + C(7,1)(4x) + C(7,2)(4x)^2 + C(7,3)(4x)^3 + C(7,4)(4x)^4 + C(7,5)(4x)^5 + ...
The fifth term corresponds to the coefficient of (4x)^4, which is given by:
C(7,4)(4)^4 = 35 x 256 = 8,960
b) To find the sixth term in the expansion of (2 - x)^11, we use the same formula as above:
(2 - x)^11 = C(11,0) + C(11,1)(-x) + C(11,2)(-x)^2 + C(11,3)(-x)^3 + C(11,4)(-x)^4 + C(11,5)(-x)^5 + ...
The sixth term corresponds to the coefficient of (-x)^5, which is given by:
C(11,5)(-1)^5(2)^6 = -11 x 32 x 32 = -11,264
c) To find the seventh term in the expansion of (3 - (2/3x))^12, we again use the same formula:
(3 - (2/3x))^12 = C(12,0) + C(12,1)(-2/3x) + C(12,2)(-2/3x)^2 + C(12,3)(-2/3x)^3 + ...
The seventh term corresponds to the coefficient of (-2/3x)^6, which is given by:
C(12,6)(-2/3)^6 = 924 x (2/3)^6 = 28.6152
9) To obtain the expansion of 2/(1-3x^2) up to the term in x^8, we can use the formula for the geometric series:
2/(1-3x^2) = 2(1 + (3x^2) + (3x^2)^2 + (3x^2)^3 + ...)
To find the term in x^8, we need to find the coefficient of (3x^2)^4:
C(n,r) = n!/[r!(n-r)!]
C(4,0) = 1, C(4,1) = 4, C(4,2) = 6, C(4,3) = 4, C(4,4) = 1
The term in x^8 is then given by:
2C(4,0) + 2C(4,1)(3x^2) + 2C(4,2)(3x^2)^2 + 2C(4,3)(3x^2)^3 + 2C(4,4)(3x^2)^4
= 2 + 24x^2 + 162x^4 + 972x^6 + 1458x^8
To learn more about expansion click on,
https://brainly.com/question/13689068
#SPJ4
if customer interarrival times are exponentially distributed with rate 6 customers per hour, then to simulate the minutes between customer arrives in excel, one would use: group of answer choices
Answers
To simulate the minutes between customer arrivals in Excel, one would use the Exponential distribution function in Excel.
This function is part of the Statistical functions category and can be found under the "Statistical" tab in Excel.
An exponential distribution is a probability distribution that describes the time between events in a Poisson process, where events occur continuously and independently at a constant average rate.
The Exponential distribution function in Excel takes two arguments: Lambda and x.
Lambda is the rate parameter, which describes the average number of events per unit of time.
In this case, the rate is 6 customers per hour, so Lambda would be equal to 6.
X is the time interval, and in this case, it would be the time between customer arrivals in minutes.
Therefore, to simulate the minutes between customer arrivals, one would use the following formula in Excel: =EXPON.DIST(x/60,1/6,TRUE)
The "x/60" part of the formula is used to convert the time interval from minutes to hours, as the rate is given in customers per hour.
The "1/6" part of the formula is used to set the Lambda value to 6.
The "TRUE" part of the formula is used to specify that we want the cumulative distribution function (CDF), which gives the probability that the time between events is less than or equal to x.
To simulate the minutes between customer arrivals in Excel, we would use the Exponential distribution function with Lambda = 6 and x being the time interval between customer arrivals in minutes.
The formula would be = EXPON.DIST(x/60,1/6,TRUE).
For similar question on distribution function.
https://brainly.com/question/30481829
#SPJ11
A study was conducted to determine whether an expectant mother's cigarette smoking has any effect on the bone mineral content of her otherwise healthy child. A sample of 77 newborns whose mothers smoked during pregnancy has mean bone mineral content x-bar1 = 0.098 g/cm and standard deviation s1 = 0.026 g/cm; a sample of 161 infants whose mothers did not smoke has mean x-bar2 = 0.095 g/cm and standard deviation s2 = 0.025 g/cm. Assume that the underlying population variances are equal.
a. Are the two samples paired or independent?
b. State the null and alternative hypotheses of the two-sided test.
c. Conduct the test at the 0.05 level of significance. What do you conclude?
Answers
Using Hypothesis testing,
a) Two samples are independent.
b)H₀: an expectant mother's cigarette smoking has any not effect on the bone mineral content of her otherwise healthy child.
Hₐ : an expectant mother's cigarette smoking has any effect on the bone mineral content of her otherwise healthy child.
c) Null hypothesis is accepted.
so, an expectant mother's cigarette smoking has no effect on the bone mineral.
We have given that,
A study which is conducted for check an expectant mother's cigarette smoking has any effect on the bone mineral content of her otherwise healthy child.
For new-born whose mother's cigarette smoking
sample size , n₁= 77
X-bar, x₁-bar = 0.098 g/cm
standard deviations, s₁ = 0.026 g/cm
For new-born whose mother did not cigarette smoking
sample size , n₂ = 161
standard deviations, s₂ = 0.025 g/cm.
mean (X-bar) , x₂-bar = 0.095 g/cm
a) the two samples are independent since they are different types of mothers, smoking mothers and non smoking mothers
b)H₀: an expectant mother's cigarette smoking has any not effect on the bone mineral content of her otherwise healthy child.
Hₐ: an expectant mother's cigarette smoking has any effect on the bone mineral content of her otherwise healthy child.
c) Test statistic:
t = (x₁-bar - x₂-bar )/S (√1/n₁+1/n₂)
where , S = √(s₁²(n₁ - 1) + s₂²(n₂ -1))/n₁+n₂ - 2
S = √((0.026)²(76) +(0.025 )²(160))/236
= 0.0253
then, t = (0.098 - 0.095 )/0.0253(√1/77 +1/161 )
=> t = 0.859
Using the critacal table critical t is
Critical t = ±1.970065
Degrees of freedom =236.0000
P-Value=0.3935 which is greater than α(0.05),
So , we accept H₀
Thus, an expectant mother's cigarette smoking has not effect on the bone mineral content of her otherwise healthy child.
To learn more about Hypothesis testing, refer:
https://brainly.com/question/4232174
#SPJ4
which property is this
(2+1) +9 = (1+2) +9
Answers
Answer: Commutative property
A supermarket gives a special
offer to cus-
tomers who purchase at least a pack of
vests and a pack of T-shirts. The offer is
restricted to a total of 7 of these items.
a) Write down three inequalities which
must be satisfied.
(b) Draw the graphs of the above condi-
tions and shade the region that satis-
fies them.
(c) If the supermarket makes a gain of N5
on each vest and N8 on each T-shirt,
find the maximum gain made by the
supermarket.
Answers
A) the three inequalities that must be satisfied are:
The number of vests, represented by x, must be a non-negative integer: x ≥ 0.The number of T-shirts, represented by y, must also be a non-negative integer: y ≥ 0.The total number of vests and T-shirts must not exceed 7: x + y ≤ 7.B) Graph shaded and satisfying all conditions is attached.
What is an inequality?An inequality in mathematics is a relationship that makes a non-equal comparison between two integers or other mathematical expressions.
It is most commonly used to compare the sizes of two numbers on a number line.
Learn more about Inequality:
https://brainly.com/question/29773201
#SPJ1

Find the measure of the missing angle

Answers
Answer: b=112 degrees and c=68
Step-by-step explanation:
Answer:
b = 112, c = 68
Step-by-step explanation:
The angle of a line is 180 degrees.
If an angle is 112, 180-112=68 so that blank space will be 68 degrees.
180-68=112, so b=112.
Since b is 112, we now that c is 68.
Can somebody help plzzzz anyone

Answers
Answer:
The answer is D.
Step-by-step explanation:
Look at the amount of zeros went over to the left so negative 3
So it’ll be 10^-3
Nacho cheese corn chips are 28,6% fat. it a party size bag contains 15 ounces of corn chips, and each gram of fat equals 9 calories, how many calories from fat are there in a party sized bag of nacho cheese corn chips?
Answers
Based on the amount of Nacho cheese corn chips and the calories per gram, the calories per party bag is 1,094.6 calories
What amount of calories are in a party bag?First, convert ounces to grams:
= 1 ounce is 28.3495 grams
Party bag in grams:
= 15 x 28.3495
= 425.243 grams
The amount of calories is:
= 425.243 x 28.6% x 9
= 1,094.6 calories
Find out more on number of calories in food at https://brainly.com/question/2456789
#SPJ4
What's the predicted number of runs for the player with only 86 hits? Show your equations, plugging in the values, and your steps to the solution. (2 points)
Answers
The predicted number of runs for the player with only 86 hits can be calculated using the equation Runs = Hits + Walks - Home Runs. Plugging in the values given, we get: Runs = 86 + Walks - Home Runs. Therefore, the predicted number of runs for the player is dependent on the number of walks and home runs they have.
To solve for the predicted number of runs, we can use the following steps:
Therefore, the predicted number of runs for the player with only 86 hits can be calculated by plugging in the values of the number of walks and home runs into the equation Runs = Hits + Walks - Home Runs.
Learn more about player
brainly.com/question/29660844
#SPJ11