Select the correct answer.
Triangle E'F'G' is the image of triangle EFG after a dilation with center at (2-3).
What is the scale factor of this dilation?
A: 2
B: 3
C: 1/2
D: 1/3

Answers
================================================================
Explanation:
Start at (2,-3). Move up 3 and over to the right 6 spots to move to (8,0) which is where point F is located.
We can write the slope as rise/run = 3/6
Go back to (2,-3). Move up 1 and to the right 2 spots to arrive at F ' (4,-2)
Let's now compare the upward movements:
Initially we moved up 3 units when trying to get to point FNow we're only moving up 1 unit when getting to F'The starting point each time is (2,-3) which is the center of dilation. The jump from 3 to 1 is "times 1/3" and that's our scale factor. Every linear distance in the image is 1/3 times as long compared to the preimage.
We can also get the same scale factor when comparing the horizontal movements as well. The jump from 6 to 2 is also "times 1/3".
Answer:
D.1/3
Step-by-step explanation:
D.1/3
Related Questions
Evaluate each geometric
series described
3 + 6 +12 + 24 n=7
Answers
1. 21+24n= 7
2. 24n= 7 - 21
3. 24n= -14
Answ: n= -7/12
How many times will Sarah have to deposit $300 every six months into her account at 4.5%
compounded semi-annually to save $10 000.00?
25.15
20.82
15.75
1458.90
Answers
With 4.5% compounded semi-annually, Sarah will need to make installments for roughly 20.82 years in order to save $10,000. Hence, 20.82 is the answer.
Is every two years or semiannually?
Simply said, semiannual refers to events that occur twice a year. A couple might commemorate their nuptials each two years, a corporation might hold workplace celebrations each two years, as well as a family might go on vacation each two years. Every two years, something that happens twice a year does.
We can utilize the calculation again for future value of an annuity to resolve this issue:
FV = P × ((1 + r/n) - 1) / (r/n)
Where:
FV = Future value
P = Periodic payment
r = Annual interest rate
n = Compounding cycles per year, number
t = Number of years
In this instance, Sarah plans to deposit $300 each six months in order to save $10,000. She will so be required to make two payments each year. P thus equals $300, n equals 2, r equals 0.045 (decimalized 4.5%), and FV equals $10,000. The number of years, t, needs to be solved for.
$10,000 = $300 × ((1 + 0.045/2) - 1) / (0.045/2)
When we simplify this equation, we obtain:
20 = (1 + 0.0225) - 1
21 = (1 + 0.0225)
Using both sides' natural logarithms:
ln(21) = ln((1 + 0.0225))
ln(21) = 2×t × ln(1 + 0.0225)
t = ln(21) / (2 × ln(1 + 0.0225))
t = 20.82
To know more about semi-annually visit:
https://brainly.com/question/20229867
#SPJ9
Use the graph to estimate the x- and y-intercepts.

Answers
The x intercept is -18 and the y intercept is 16
Step-by-step explanation:
Hello there!
In order to find the x and y intercepts, we need to find where the line is intercepting the x and y lines
The x coordinates are on the line that is horizontal, and the y coordinates are on the line that is vertical.
The line is hitting the y coordinate (0, 16)
This means, the y intercept is 16
Now we need to find the x intercept
Since the line isn't clearly hitting a coordinate, we need to estimate the most proper answer
As you can see, the coordinates are going up by increments of 4
In this case, since we are looking at the negatives, it is going down by 4
Now the line is hitting the x coordinates at around halfway between two numbers
And since the numbers are going down by 4, half of it would be going down by 2
Meaning, that the x intercept would be 2 below -16
And 2 below -16 is -18
This means, the x intercept is -18
At a baseball game, a vender sold a combined total of 191 sodas and hot dogs. The number of hot dogs sold was 47 less than the number of sodas sold. Find the number of sodas sold and the number of hot dogs sold.
Answers
The number of sodas sold at the baseball game was 119, while the number of hot dogs sold was 72.
Let's assume the number of sodas sold as 'x' and the number of hot dogs sold as 'y'.
According to the problem, the total number of sodas and hot dogs sold is 191, so we can write the equation:
x + y = 191 ...(1)
The problem also states that the number of hot dogs sold was 47 less than the number of sodas sold. Mathematically, we can express this as:
y = x - 47 ...(2)
To find the values of x and y, we can solve the system of equations (1) and (2). Substituting equation (2) into equation (1), we have:
x + (x - 47) = 191
Simplifying the equation:
2x - 47 = 191
2x = 191 + 47
2x = 238
Dividing both sides by 2:
x = 238/2
x = 119
Substituting the value of x back into equation (2):
y = 119 - 47
y = 72
As a result, the total amount of sodas sold is 119, and the total amount of hot dogs sold is 72.
For more such questions on number, click on:
https://brainly.com/question/24644930
#SPJ8
In a video game, Clare scored 50% more points than Tyler. If c is the number of points that Clare scored and t is the number of points Tyler scored, which equations, are correct?
Answers
Answer:
c= 1.5t, c=t+0.5t and c=(1+0.5)t
Step-by-step explanation:
Given that, Clare scored 50% more points than Tyler, c is the number of points that Clare scored and t is the number of points that Tyler scored,According to question,c = 150% of tc = 1.5tHence, the correct options are c = 1.5t, c = t+0.5t and c = (1+0.5)t
HELPEHELP
Morgan took a taxi from her house to the airport. The taxi company charged a pick- up fee of $1.80 plus $2.50 per mile. The total fare was $59.30, not including the tip. Which equation or tape diagram could be used to represent the context if x represents the number of miles in the taxi ride?
Answers
Answer:
The equation should be 2.5x+1.8=59.3
Step-by-step explanation:
First, subtract the 1.8 dollars from the 59.3. You will get 57.5. Divide it by 2.5 and you will get the number 21 as x.
What is the M.A.D. (mean absolute deviation) of the following data set?
8 9 9 7 8 6 9 8
Answers
The mean absolute deviation is 0.75
How to determine the mean absolute deviationTo calculate the mean absolute deviation (M.A.D.), you need to find the average of the absolute differences between each data point and the mean of the data set
From the information given, we have that the data set is;
8 9 9 7 8 6 9 8
Let's calculate the mean, we get;
Mean = (8 + 9 + 9 + 7 + 8 + 6 + 9 + 8) / 8
Mean = 64 / 8
Divide the values
Mean = 8
Let's determine the absolute difference, we get;
Absolute differences=
|8 - 8| = 0
|9 - 8| = 1
|9 - 8| = 1
|7 - 8| = 1
|8 - 8| = 0
|6 - 8| = 2
|9 - 8| = 1
|8 - 8| = 0
Find the mean of the absolute differences:
Average of absolute differences = (0 + 1 + 1 + 1 + 0 + 2 + 1 + 0) / 8
Absolute difference = 6 / 8 = 0.75
Learn more about mean absolute deviation at: https://brainly.com/question/447169
#SPJ1
Select the correct answer.
What is this expression in simplest form?
1/2x^2-4x - 2/x
A. 4x-7/2x(x-2)
B. -4x+9/2x(x-2)
C. -1/2x(x-2)
D. -3x-8/2x(x-2)
Answers
Answer:a A. 4x-7/2x(x-2)
got it right on the test
Step-by-step explanation:
plSSSSSssssssssssssSsSsS

Answers
Answer:
78.54
Step-by-step explanation:
The formula is \(A = \pi r^2\\\). So, substitute the values into the equasion and get the answer.
According to the order of operations, we square the radius first, then multiply by pi. 5^2 = 25. 25 * pi = 78.5398163397. I just rounded it to the nearest hundereth.
What is x .
ABC~ DEF

Answers
Answer:
Dado, △ABC∼△DEF
Por lo tanto
DE
=
EF
A.C
=
FD
CA
Así que
18
2x−1
=
3x+9
2x+2
=
6x
3x
Ahora tomando
18
2x−1
=
6x
3x
tenemos
18
2x−1
=
2
1
o 4x−2=18 o x=5
Por lo tanto, AB=2×5−1=9,
BC=2×5+2=12,CA=3×5=15,
DE=18,EF=3×5+9=24
y FD=6×5=30
Por lo tanto
AB = 9 cm, BC = 12 cm, CA = 15 cm, DE = 18 cm, EF = 24 cm y FD = 30 cm
:
Write is 8.517 in expanded form
Answers
Answer: (8 x 1) + (5/10) + (1/100) + (7/1000)
Step-by-step explanation: Have a blessed day hopefully this helped!
Answer:
8 tens, 5 tenths, 1 hundredth, 7 thousandths
Step-by-step explanation:
Hope I helped give brainliest if right :D
Write the equation for the function graphed below

Answers
Answer:
Step-by-step explanation:
looks to be a parabola, so use vertex mode (h, k) = (-1, 2)
y = a(x - h)² + k
y = a(x + 1)² + 2
another point on the curve seems to be (1, 6)
6 = a(1 + 1)² + 2
1 = a
y = (x + 1)² + 2
or expand for standard form y = ax² + bx + c
y = (x² + 2x + 1) + 2
y = x² + 2x + 3
What is the slope of the following line?

Answers
Answer:c, the answer is c
Step-by-step explanation:
A furniture company is introducing a new line of lounge chairs next quarter. These are the cost and revenue functions, where x represents the number of chairs to be manufactured and sold: R(x) = 1,248x – 8.32x2 C(x) = 36,400 – 83.2x
Answers
The profit function for a furniture company introducing a new line of lounge chairs is P(x) =\(-8.32x^2 + 1,248x - 36,400\), where x represents the number of chairs to be manufactured and sold.
The problem provides the revenue function and cost function for a furniture company introducing a new line of lounge chairs. To find the profit function, we need to subtract the cost function from the revenue function.
The revenue function R(x) is given as 1,248x - \(8.32x^2\), where x represents the number of chairs manufactured and sold. This function calculates the total revenue obtained by the company by multiplying the number of chairs sold (x) by the price of each chair (1,248 - 8.32x).
The cost function C(x) is given as 36,400 - 83.2x. This function calculates the total cost incurred by the company to manufacture x chairs, which includes both fixed and variable costs.
To find the profit function for the furniture company, we need to subtract the cost function C(x) from the revenue function R(x):
P(x) = R(x) - C(x) = (1,248x - \(8.32x^2\)) - (36,400 - 83.2x)
Simplifying this expression, we get:
P(x) =\(-8.32x^2\) + 1,248x - 36,400
Therefore, the profit function for the furniture company is P(x) = \(-8.32x^2\) \(+ 1,248x - 36,400\).
To learn more about cost function please click on below link
https://brainly.com/question/31041336
#SPJ1
What formula do I use for this? How do I get the points to graph?

Answers
The graph of the function y = 5|x - 4| is added as an attachment
Sketching the graph of the functionFrom the question, we have the following parameters that can be used in our computation:
y = 5|x - 4|
The above function is an absolute value function that has been transformed as follows
Vertically stretched by a factor of 5Shifted right by 4 unitsNext, we plot the graph using a graphing tool by taking not of the above transformations rules
The graph of the function is added as an attachment
Read more about functions at
brainly.com/question/2456547
#SPJ1

2) LaChina spherical glass decorative balls that she is filling with blue liquid to match the color of
her room. If there is 4,000 cubic inches of liquid to be poured into 20 glass spheres, what is the
diameter of each sphere? Round to two decimal.
Answers
Answer:
8000
Step-by-step explanation:
A bucket contains 72 red, 48 blue, 48 green, and 48 yellow crayons. The art teacher also has 120 pieces of drawing paper. What is the largest number of identical kits the art teacher can make with all of the crayons and all of the paper?
Answers
The art teacher can make a maximum of 24 identical kits using all the crayons and drawing paper for proper distribution.
To determine the largest number of identical kits the art teacher can make using all the crayons and drawing paper, we need to find the greatest common divisor (GCD) of the quantities.
The GCD represents the largest number that can divide all the quantities without leaving a remainder.
The GCD of the quantities of crayons can be found by considering the prime factorization:
72 = 2³ × 3²
48 = 2⁴ × 3
48 = 2⁴ × 3
48 = 2⁴ × 3
The GCD of the crayons is 2³ × 3 , which is 24.
Now, we need to find the GCD of the quantity of drawing paper:
120 = 2³ × 3 × 5
The GCD of the drawing paper is also 2³ × 3 , which is 24.
Since the GCD of both the crayons and drawing paper is 24, the art teacher can make a maximum of 24 identical kits using all the crayons and drawing paper.
Each kit would contain an equal distribution of crayons and drawing paper.
Learn more about distribution here:
brainly.com/question/30034780
#SPJ1
The U.S. Department of Agriculture claims that the mean consumption of coffee by a person in the United States is 24.2 gallons per year. A random sample of 101 people in the United States shows that the mean coffee consumption is 23.5 gallons per year with a standard deviation of 3.2 gallons. At α=0.05, can you reject the claim? Using a P-value, evaluate the claim. Using Rejection Regions for a z-test, evaluate the claim.
Answers
Answer:
The decision rule is
Reject the null hypothesis
The conclusion is
There is sufficient evidence to reject the claim
Step-by-step explanation:
From the question we are told that
The population mean is \(\mu = 24.2 \ gallons \ per \ year\)
The sample size is n = 101
The sample mean is \(\= x = 23.5 \ gallons\ per\ year\)
The standard deviation is \(\sigma = 3.2 \ gallons\)
The null hypothesis is \(H_o : \mu = 24.2\)
The alternative hypothesis is \(H_a : \mu \ne 24.2\)
Generally the test statistics is mathematically represented as
\(z = \frac{ \= x - \mu }{ \frac{\sigma }{ \sqrt{n} } }\)
=> \(z = \frac{ 23.5 - 24.2 }{ \frac{ 3.2}{ \sqrt{ 101} } }\)
=> \(z = -2.198\)
From the z table the area under the normal curve to the left corresponding to -2.198 is
\(P(Z < -2.198 ) = 0.013975\)
Gnerally the p-value is mathematically represented as
\(p-value = 0.013975 * 2\)
=> \(p-value = 0.02795\)
From the value obtained we have that \(p-value \ < \ \alpha\) hence
The decision rule is
Reject the null hypothesis
The conclusion is
There is sufficient evidence to reject the claim
Using the Rejection Regions for a z-test method
Generally from the z table the critical value of \(\frac{\alpha }{2}\) is
\(z_{critical} = \pm 1.96\)
Not we are using \(\frac{\alpha }{2}\) because it is a two - tailed test
Now comparing the critical value and the test statistics we see that the
region covered by the test statistics (i.e \(2.198 < z < -2.198\)) is greater than the region covered by the critical value (i.e \(1.96 < z < -1.96\))
Hence
The decision rule is
Reject the null hypothesis
The conclusion is
There is sufficient evidence to reject the claim
An ice cream shop finds that its weekly profit P (measured in dollars) as a function of the price x (measured in dollars) it charges per ice cream cone is given by the function k, defined by k(x) = 125x^2 +670x 125 where P= k(x).
Required:
a. Determine the maximum weekly profit and the price of an ice cream cone that produces that maximum profit
b. The cost of the ice cream cone is too low then the ice cream shop will not make a profit. Determine what the ice cream shop needs to charge in order to break even
c. The profit function for Cold & Creamy (another ice cream shop) is defined by the function g where gx)- k(x-2). Does the function g have at the same maximum value as k?
Answers
Answer:
The answer is below
Step-by-step explanation:
Given that k(x) = -125x² +670x - 125, where x is the charge per cone and P = k(x) is the weekly profit
a) The maximum profit is at P'(x) = 0. Therefore we have to find the derivative of the profit equation and equate it to 0.
P'(x) = k'(x) = 0
k'(x) = -250x + 670 = 0
-250x + 670 = 0
250x = 670
x = $2.68
P = k(2.68) = -125(2.68²) + 670(2.68) - 125 = $772.8
Hence the maximum profit is $772.8 when the price of each ice cream cone is $2.68
b) At break even, the profit is 0. Hence P= k(x) = 0
-125x² + 670x - 125 = 0
x = 5.17 or x = 0.19
Therefore to break even, the price of the ice cream cone needs to be $0.19 or $5.17
c) g(x) = k(x - 2)
g(x) = -125(x - 2)² + 670 (x -2) - 125
Maximum profit is at g'(x) = 0
g'(x) = -250(x-2) + 670
-250(x-2) + 670 = 0
-250x + 500 + 670 = 0
250x = 1170
x = 4.68
g(4.68) = -125(4.68 - 2)² + 670(4.68 -2) - 125 = $772.8
Therefore function g has the same maximum value as function k
In a pre algebra class containing 43 students, there are 4 freshman, 35 sophomores, and 4 juniors. what fraction of the class are sophomores
Answers
The fraction of the class that is sophomores is \(35/43\).
The fraction of the class that is sophomores, divide the number of sophomores by the total number of students in the class.
Number of sophomores = 35
Total number of students = 43
Fraction of sophomores = (Number of sophomores)/(Total number of students Fraction of sophomores)
Fraction of sophomores \(= 35 / 43\)
Therefore, the fraction of the class that are sophomores is = \(35/43\).
To learn more about Fraction here,
https://brainly.com/question/10354322
g A population consists of twenty bowerbirds, six of which have bowers featuring reflective decor. If three of the bowerbirds are randomly sampled with replacement from this population, what is closest to the expected number of them that have bowers featuring reflective decor?Group of answer choices00.90.953
Answers
Answer:
a ) 0.9
Expected number of bower-birds that have bowers featuring reflective decor
μ = 0.9
Step-by-step explanation:
Explanation:-
Given Sample size 'n' = 20
Given data A population consists of twenty bower-birds, six of which have bowers featuring reflective decor.
probability of success
\(p = \frac{x}{n} = \frac{6}{20} =0.3\)
Given three of the bower-birds are randomly sampled with replacement from this population.
So we will choose sample size 'n'= 3
Let 'X' be the random variable in binomial distribution
Expected number of bower-birds that have bowers featuring reflective decor
μ = n p
= 3 × 0.3
=0.9
conclusion:-
Expected number of bower-birds that have bowers featuring reflective decor
μ = 0.9
Is 3/4 a rational expression? Explain.
Answers
Answer:
this is your answerStep-by-step explanation:
I hope it's helpful bro ✌️

help thank you, this is my sisters homework

Answers
The answers for the given multiplication chart are given below:
What is meant by multiplication?One of the four basic mathematical operations of arithmetic, together with addition, subtraction, and division, multiplication is frequently represented by the cross symbol.
When two numbers are multiplied, they are added in the same amount of copies of the multiplicand and multiplier, which is how repeated addition can be thought of when multiplying whole numbers. Another way to think about multiplication is to count the objects that are arranged in a rectangle (for whole numbers) or to calculate the area of a rectangle whose sides have a certain length.
X 2 -4 -9 6 3 8 -1 4 -8 -2 -6 7 -5 9 -7
-3 -6 12 27 -18 -9 -24 3 -12 24 6 18 -21 15 -27 21
9 18 -36 -81 54 27 72 -9 36 -72 -18 -54 63 -45 81 -63
-6 -12 24 54 -36 -18 -48 6 -24 48 12 36 -42 30 -54 42
5 10 -20 -45 30 15 40 -5 20 -40 -10 -30 35 -25 45 -35
-7 -14 28 63 -42 -21 -56 7 -28 -56 -14 42 -49 35 -63 49
To know more about multiplication, visit:
https://brainly.com/question/12617401
#SPJ1
Please help!With steps and explanation

Answers
9514 1404 393
Answer:
dy/dx = (2 -x)/40.005Step-by-step explanation:
(a) Solving the x-equation for u gives ...
u = (x -1)/4
Differentiating both equations with respect to u, we have ...
dy/du = 1 -4u
dx/du = 4
Then dy/dx is ...
dy/dx = (dy/du)/(dx/du) = (1 -4u)/4
Substituting for u gives ...
dy/dx = (1 -4(x -1)/4)/4
dy/dx = (2 -x)/4
__
(b) The approximate change in y is ...
∆y ≈ (dy/dx)(∆x)
For ∆x = 2.98 -3.00 = -0.02, and x=3, the approximate change is ...
∆y ≈ (2 -3)/4(-0.02)
∆y ≈ 0.005
Last question: Find the volume of a cylinder where the circular base has a diameter of 7km, and the height of the cylinder is 13.08km.
Note: Find the indicated volumes. Use 3.14 for pi and round your final results two decimal places as needed

Answers
Answer:
503.1222
rounded: 503.12
If Tevin has 2 times as many dimes as nickels and they have a combined value of 100 cents, how many of each coin does he have?
dimes____
nickels____
Answers
Answer:
dimes- 8
nickels- 4
Step-by-step explanation:
dime=10 cents
nickels=5 cents
5 x 4 = 20
10 x 8 = 80
80 + 20 = 100
... please give brainliest ...
A vehicle moves along a straight road. The vehicle's position is given by f(t), where t is measured in seconds since the vehicle starts moving. During the first 10 seconds of the motion, the vehicle's acceleration is proportional to the cube root of the time since the start. Which of the following differential equations describes this relationship, where k is a positive constant?
a. df/dt= k3√t
b. df/dt= k3√f
c. d^2f/dt^2= k3√t
d. d^2f/dt^2= k3√f
Answers
Answer:
C. \(\frac{d^{2}f}{dt^{2}} = k\cdot \sqrt[3] {t}\)
Step-by-step explanation:
Physically speaking, the acceleration is equal to the second derivative of the position of the vehicle in time. After a careful reading to the statement, we construct the following ordinary differential equation:
\(\frac{d^{2}f}{dt^{2}} = k\cdot \sqrt[3] {t}\)
Where:
\(t\) - Time, measured in seconds.
\(k\) - Proportionality constant, measured in meters per second up to 7/3.
Therefore, the correct answer is C.
The differential equation that models the situation is:
\(\frac{d^2f}{dt^2} = k\sqrt[3]{t}\)
Which is option C.
The position is the integral of the acceleration, with is the integral of the acceleration, hence, the relation between the position and the acceleration is:
\(\frac{d^2f}{dt^2}\)
The acceleration is proportional to the cube root of the time since the start, hence:
\(\frac{d^2f}{dt^2} = k\sqrt[3]{t}\)
In which k is the constant of proportionality.
A similar problem is given at https://brainly.com/question/14480252
A cylinder has a radius of 4 millimeters. Its volume is 200.96 cubic millimeters. What is the height of the cylinder?
Answers
Answer:
3.999 millimeters.
Step-by-step explanation:
To find the height of the cylinder, we can use the formula for the volume of a cylinder:
V = πr²h
Given that the radius (r) of the cylinder is 4 millimeters and the volume (V) is 200.96 cubic millimeters, we can substitute these values into the formula and solve for the height (h).
200.96 = π(4²)h
200.96 = 16πh
To solve for h, we can divide both sides of the equation by 16π:
200.96 / (16π) = h
Using a calculator, we can calculate the approximate value of h:
h ≈ 200.96 / (16 × 3.14159)
h ≈ 3.999
Therefore, the height of the cylinder is approximately 3.999 millimeters.
If Triangle AGM~ Triangle KXD, find the value of x.

Answers
Answer:
60*
Step-by-step explanation:
i think its a equalateral triangle so if so all the angles are 60 degrees
This solution means in month 2 (that is, February), both functions have the same value (f(2) = g(2) = 4), which means the number of imports and the number of exports are the same.
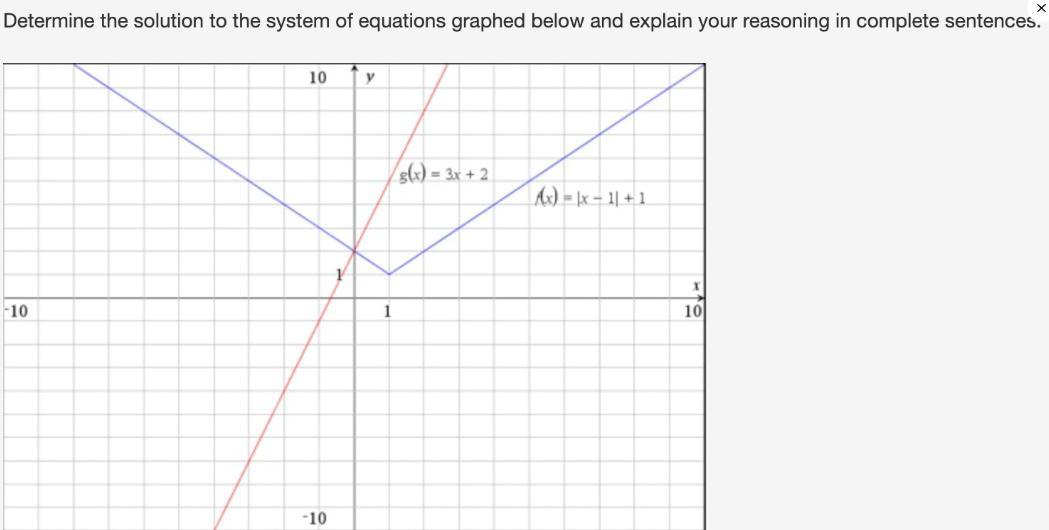
Answers
To determine the solution of a system of equations graphed you identify the point of intersection of the graphs as that is the values that the functions share. The functions in the system have the same values in the point of intersection.
Then, the solution for the given system is (0,2)