Show that the following series are convergent and find their sums:
1/ 1×2×3 + 1/2×3×4+…+1/n(n+1)(n+2)+…

The statement (∀z)(∀y)[(G(z) & W(y)) → E(y,z)] would be false under the circumstance described in option d, i.e., if there is a single wolf that has eaten every goat.

The given statement can be translated as "For all z (goats) and y (wolves), if z is a goat and y is a wolf, then y has eaten z." In other words, it asserts that every goat is eaten by a wolf.

Option d contradicts this statement by stating that there is a single wolf that has eaten every goat. If there exists a wolf that has consumed all the goats, then the statement (∀z)(∀y)[(G(z) & W(y)) → E(y,z)] would be false because not every goat is eaten by a wolf in that scenario. Therefore, option d represents the circumstance in which the statement would be false.


To learn more about statements click here: brainly.com/question/29751060

#SPJ11

Answer:

0. 25 25/100

Step-by-step explanation:

The quadratic equation with zeros at -6 and 2 is y² + 4y - 12 = 0. This is in standard form, which is ax² + bx + c = 0, with a = 1, b = 4, and c = -12.

To find the quadratic equation with zeros at -6 and 2, we can start by using the fact that if a quadratic equation has roots x₁ and x₂, then it can be written in the form

(y - x₁)(y - x₂) = 0

where y is the variable in the quadratic equation.

Substituting the given values of the zeros, we get

(y - (-6))(y - 2) = 0

Simplifying this expression, we get

(y + 6)(y - 2) = 0

Expanding this expression, we get

y² - 2y + 6y - 12 = 0

Simplifying this expression further, we get

y² + 4y - 12 = 0

So the quadratic equation with zeros at -6 and 2 is

y² + 4y - 12 = 0

This is the standard form of a quadratic equation, which is

ax² + bx + c = 0

where a, b, and c are constants. In this case, a = 1, b = 4, and c = -12.

To know more about quadratic equation:

https://brainly.com/question/30098550

#SPJ1

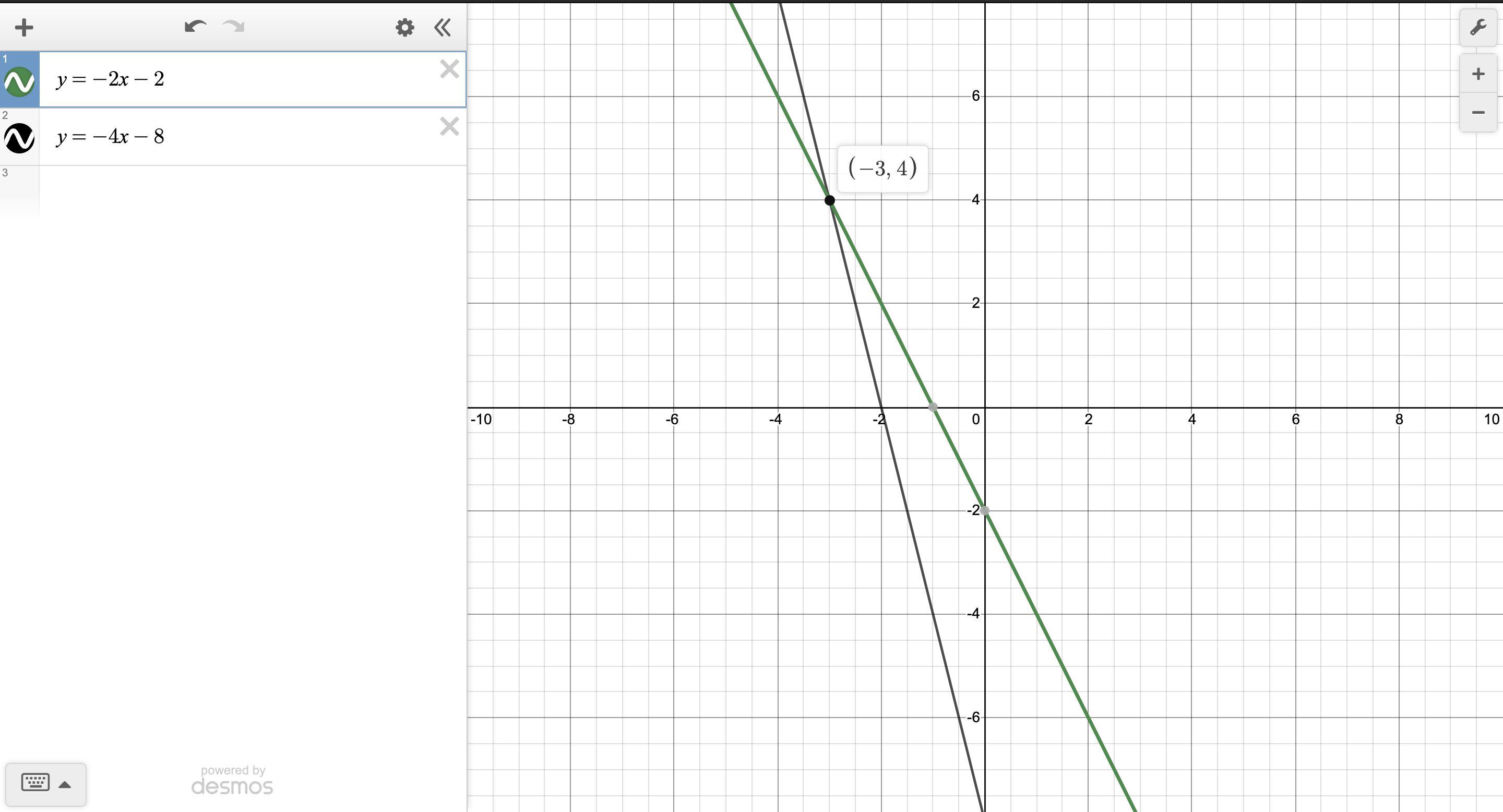
Answer:

Step-by-step explanation: you need to dived by3000

The given system of differential equations can be analyzed using a Lyapunov function of the form ax^2 + cy^2, where a and c are to be determined. By computing the derivative of this function along the trajectory of the system, we can determine the stability properties of the critical point at the origin.

First, we compute the derivative of the Lyapunov function along the trajectory of the system:

V'(x,y) = 2ax(x^3 + xy^2) + 2cy(xy' - 2x^2y)

Using the second equation of the system, we can substitute y' = x^3 + xy^2 - 2x^2y to obtain:

V'(x,y) = 2ax(x^3 + xy^2) + 2cy(x^3 + xy^2 - 2x^2y - 2x^2y)

Simplifying this expression yields:

V'(x,y) = 2x(x^2 + y^2)(a + c - 4ac)

For the critical point at the origin to be asymptotically stable, we need V'(x,y) to be negative definite in a neighborhood of the origin. This can be achieved by choosing a and c such that a + c - 4ac < 0 and a, c > 0. For example, we can choose a = 1/4 and c = 1/2, which gives a + c - 4ac = -1/4.

Therefore, the critical point at the origin is asymptotically stable. This means that any trajectory that starts sufficiently close to the origin will converge to the origin as t approaches infinity. The Lyapunov function provides a way to analyze the stability of the critical point without solving the system explicitly, which can be useful for more complex systems.

To learn more about equations click here: brainly.com/question/24169758

#SPJ11

Answer:

28x

Step-by-step explanation:

Move the y = x2 graph 10 units to the right, then 8 units up.

There are y= x²——————> y = (x-10)²+8

The fact that

A point (x,y) in f(x) shifts up by d as a result of f(x)+d, a

and

f(x-e) ----> a point (x, y) in f(x) becomes a——————-> (x+e, y)——> shift right by  in this issue

d=8

e=10

Therefore,

Shift the y = x2 graph.

8 up, 10 to the right

The law is

(x,y)———-> (x+10,y+8)

The vertex in the equation y=x2--------- (0,0)

The vertex in the equation y = (x-10)2+8 (10,8)

so

(10,8)------> (0,0)----------> (x+10,y+8)———> (10,8)------> (0+10,0+8)

As a result, shift the y = x2 graph 8 units up and then 10 units to the right.

Learn more about graphs at

https://brainly.com/question/10478597

#SPJ9

Option a, adjacency matrix. An adjacency matrix is a two-dimensional array that represents a graph's edges, where the rows and columns correspond to the vertices of the graph. If there is an edge between two vertices, the corresponding element in the matrix is set to 1, otherwise it is set to 0. This implementation is useful for dense graphs, where the number of edges is close to the maximum possible number of edges.

An adjacency matrix is a simple and efficient way to represent graphs that have a large number of vertices and edges. It allows for fast lookups of the existence of an edge and is useful for various algorithms that require graph representation. However, it is not suitable for sparse graphs, where the number of edges is much smaller than the maximum possible number of edges. In such cases, an adjacency list would be more appropriate.

The common implementation of a graph that uses a two-dimensional array to represent the graph's edges is called an adjacency matrix.

To know more about array representation,visit:

https://brainly.in/question/5489688

#SPJ11

the vector equation for the line segment from (3, -4, 4) to (7, 2, 3) is:

r = <3, -4, 4> + t<4, 6, -1>

We can find a vector equation for the line segment by first finding the direction vector of the line segment, and then using it to write the equation in vector form.

The direction vector of the line segment is the difference between the two endpoints:

d = <7, 2, 3> - <3, -4, 4> = <4, 6, -1>

To write the vector equation in terms of the parameter t, we can use the parametric form of the equation of a line:

r = r_0 + td

where r is the position vector of a point on the line, r_0 is the position vector of a known point on the line (in this case, (3, -4, 4)), t is a scalar parameter, and d is the direction vector we just found.

Substituting the values we know, we get:

r = <3, -4, 4> + t<4, 6, -1>

To know more about vector visit:

brainly.com/question/24256726

#SPJ11

The z value that leaves area 0.1056 in the right tail is approximately 1.26.

The z value that leaves an area of 0.1056 in the right tail is found by using the standard normal distribution table or a z-score calculator.

Here's how to find it:

1. Since the area to the right of the z value is 0.1056, the area to the left will be 1 - 0.1056 = 0.8944.

2. Look up the corresponding z value for the area 0.8944 in a standard normal distribution table or use a z-score calculator.

3. Find the z value associated with this area.

After performing these steps, you will find that the z value that leaves an area of 0.1056 in the right tail is approximately 1.26.

Learn more about z value: https://brainly.com/question/25638875

#SPJ11

Answer:

x = -3

Step-by-step explanation:

2x + y = -2

4x + y = -8

2x + y = - 2

y = -2x - 2

4x + y = - 8

y = -4x - 8

y = -2x - 2

y = -4x - 8

-2x - 2 = -4x - 8

4x - 2x = 2 - 8

2x = -6

2x/2 = -6/2

x = -3

To check just use da graph ;w;

The x is -3

Answer:

Step-by-step explanation:

x=  −1 −y/2

​

x= 4 −8−y/4

​

The right triangle, like the other triangles, has three sides, three vertices, and three angles. The difference between the other triangles and the right triangle is that the right triangle has a 90  angle.

To find missing angles and sides and round to the nearest tenth, you can use different methods depending on the given information and the type of triangle or shape involved.

Some common methods include:
Trigonometric ratios (sine, cosine, tangent) for right triangles.
Angle sum property or exterior angle property for triangles.
Pythagorean theorem for right triangles.
Law of cosines and law of sines for non-right triangles.
To help find the missing angles and sides of a triangle, you need certain information about the triangle, such as known angle and side measurements, or information about the properties of the triangle.

Without this information, no concrete calculations can be made.

Provide the necessary information or describe the problem in more detail and we will help you find the missing corners and sides of the triangle and round it to tenths.

Remember to always check if any additional information is given, such as side lengths or angles ' 7 and to apply the appropriate formula or property to find the missing value.

Round your answer to the nearest tenth as specified.

For more related questions on right triangle:

https://brainly.com/question/2773823

#SPJ8

Answer:

2.19

Step-by-step explanation:

Hope this helps and have a great day!!!!

The expression to represent the statement 5 times the sum of x and 3 is 5 * (x + 3)

from the question, we have the following parameters that can be used in our computation:

5 times the sum of x and 3

times as used here means product

So, we have

5 * the sum of x and 3

the sum of as used here means addition

So, we have

5 * (x + 3)

Hence, the expression to represent the statement is 5 * (x + 3)

Read more about expression at

https://brainly.com/question/15775046

#SPJ1

Question

Write an expression to represent: 5 times the sum of x and 3

Answer:

(g ￮ f)(x) = x² + 8x + 15

Step-by-step explanation:

to find (g ￮ f)(x) substitute x = f(x) into g(x)

(g ￮ f)(x)

= g(f(x))

= g(x + 4)

= (x + 4)² - 1 ← expand factor using FOIL

= x² + 8x + 16 - 1 ← collect like terms

= x² + 8x + 15

Answer:

The coordinate of the initial point is given below as

The coordinate of the terminal point is

Concept:

The formula below will be used to calculate a linear form of v

By substituting the values, we will have

Hence,

The final answer is

The FIRST OPTION is the right answer

The final amount is approximately $58,353.52.

The total interest earned on the original investment is $23,353.52.

(a) To find the semiannual interest rate, we divide the annual interest rate by the number of compounding periods per year. In this case, since interest is compounded semiannually, we divide 7.8% by 2:

Semiannual interest rate = 7.8% / 2 = 3.9%

(b) Similarly, to find the quarterly interest rate, we divide the annual interest rate by the number of compounding periods per year. Since there are 4 quarters in a year, we divide 7.8% by 4:

Quarterly interest rate = 7.8% / 4 = 1.95%

(c) To find the monthly interest rate, we divide the annual interest rate by the number of compounding periods per year. Assuming 12 months in a year, we divide 7.8% by 12:

Monthly interest rate = 7.8% / 12 = 0.65%

(a) To find the final amount, we use the formula for compound interest:

Final amount = Principal × (1 + interest rate)^number of years

Final amount = $35,000 × (1 + 7.5%)^8 ≈ $58,353.52

Therefore, the final amount is approximately $58,353.52.

(b) The total interest earned on the original investment can be calculated by subtracting the principal amount from the final amount:

Total interest = Final amount - Principal

Total interest = $58,353.52 - $35,000 = $23,353.52

Therefore, the total interest earned on the original investment is $23,353.52.

Know more about Semiannually here:

https://brainly.com/question/31425733

#SPJ11

Step-by-step explanation:

1, 19 and 1, 2, 19, 38 respectively.

I think this is ur answer.....!

Answer:

The answer is below

Step-by-step explanation:

The question is not complete. A similar question is attached and is solved.

Solution:

A triangle is a polygon with three sides and three angles. Types of triangles are scalene, acute, obtuse, isosceles, equilateral and right angled triangle.

A right angled triangle is a triangle with one angle equal to 90 degrees. The longest side of a right angled triangle is known as the hypotenuse. Trigonometric identities is used to show the relationship between the angles and sides of a right angled triangle, i.e.:

sinθ = opposite/hypotenuse; cosθ = adjacent / hypotenuse; tanθ = opposite / adjacent

From the image:

let the distance from jack to the base of the building be x, hence:

tan60 = x / 60

x = 60 * tan60 = 104 ft.

Answer:

7. -27 + 6y = 3y - 9

6y-3y = -9+27

3y = 18

3=6

8. 3(m-2) = -2(m-3)

3m-6 = -2m + 6

3m+2m= 6+6

5m=12

m= 12/5

Answer:

50

Step-by-step explanation:

From the given information provided, the value of the expression (-14⁰)⁻²

is 1 that is option d.

We need to follow the order of operations, which is to evaluate any exponents first, before performing any other operations.

Exponent rules are mathematical rules that describe how to simplify expressions that involve exponents.

(-14⁰)⁻² can be simplified as follows:

(-14⁰)⁻² = (-1)⁰ × 14⁰ × (-1)⁻² [Using the rule (\(a^m\))ⁿ = \(a^(m*n)\)]

(-14⁰)⁻² = 1 × 1 × 1/(-1)⁻² [Using the rule a⁰ = 1]

(-14⁰)⁻² = 1 × 1 × 1/1

(-14⁰)⁻² = 1

Therefore, the value of (-14⁰)⁻² is 1. Answer: d) 1

Learn more about exponent here: brainly.com/question/11975096

#SPJ4

If the RMS value of the sinusoidal input to a full wave rectifier is Vo / (2)^(1/2) then the RMS value of the rectifier’s output is  \(Vo * (2)^(1/2) / 2.\)

Full wave rectifier length = Vo / (2)^(1/2)

The peak value of the output voltage = Vo.

For a full-wave rectifier, the outcome voltage is the whole value of the input voltage.

The RMS value of a sinusoidal waveform can be calculated using the formula:

Vrms = Vp / \((2)^(1/2)\)

Vrms = Vo / \((2)^(1/2)\)

To simplify this equation, we can multiply both the numerator and the denominator by (2)^(1/2):

\(Vrms = (Vo / (2)^(1/2)) * ((2)^(1/2)/(2)^(1/2))\)

\(Vrms = Vo * (2)^(1/2) / 2\)

Therefore, we can conclude that the RMS value of the rectifier's output is \(Vo * (2)^(1/2) / 2.\)

To learn more about Rectifier

https://brainly.com/question/14661951

#SPJ4

\(\displaystyle\\Answer:\ none \ of\ these\ (m=-\frac{5}{3} );\ isosceles,\ right\)

Step-by-step explanation:

1.

a) find the midpoint G of the side DE:

\(x_D=-2\ \ \ \ x_E=3\ \ \ \ y_D=-2\ \ \ \ y_E=1\)

\(\displaystyle\\x_G=\frac{x_D+x_E}{2} \\\\x_G=\frac{-2+3}{2}\\\\x_G=\frac{1}{2}\\\\x_G=0.5\)

\(\displaystyle\\y_G=\frac{y_D+y_E}{2}\\\\y_G=\frac{-2+1}{2} \\\\y_G=\frac{-1}{2} \\\\y_G=-0.5\\\\Thus,\ G(0.5,-0.5)\)

b) find the midpoint I of the side DF:

\(x_D=-2\ \ \ \ x_F=6\ \ \ \ y_D=-2\ \ \ \ y_F=-4\)

\(\displaystyle\\x_I=\frac{x_D+x_F}{2} \\\\x_I=\frac{-2+6}{2} \\\\x_I=\frac{4}{2} \\\\x_I=2\)

\(\displaystyle\\y_I=\frac{y_D+y_F}{2}\\\\y_I=\frac{-2+(-4)}{2}\\\\y_I=\frac{-6}{2} \\\\y_I=-3\\\\Thus,\ I(2,-3)\)

c) the slope of GI:

\(x_G=0.5\ \ \ \ x_I=2\ \ \ \ y_G=-0.5\ \ \ \ y_I=-3\)

\(\displaystyle\\m_{GI}=\frac{y_I-y_G}{x_I-x_G} \\\\m_{GI}=\frac{-3-(-0.5)}{2-0.5} \\\\m_{GI}=\frac{-3+0.5}{1.5} \\\\m_{GI}=\frac{-2.5}{1.5} \\\\m_{GI}=\frac{-2.5(2)}{1.5(2)} \\\\m_{GI}=-\frac{5}{3}\)

2.

Type of Δ DEF:

a) find the length of the side DE:

\(|DE|=\sqrt{(3-(-2)^2+(1-(-2)^2}\\\\|DE|=\sqrt{(3+2)^2+(1+2)^2} \\\\|DE|=\sqrt{5^2+3^2}\\\\|DE|=\sqrt{25+9} \\\\|DE|=\sqrt{34} \ units\)

b) find the length of the side EF:

\(|EF|=\sqrt{(6-3)^2+(-4-1)^2}\\\\|EF|=\sqrt{3^2+(-5)^2}\\\\ |EF|=\sqrt{9+25} \\\\|EF|=\sqrt{34}\ units\)

Hence, DE=EF

c)  find the m∠DEF:

\(\displaystyle\\cos \angle E=\frac{\overrightarrow {DE}+\overrightarrow {EF}}{|DE|*|EF|} \\\\\)

Find the coordinates of the vector by the coordinates of its beginning and end points:

\(\displaystyle\\\overrightarrow {DE}=(x_E-x_D,y_E-y_D)\\\\\overrightarrow {DE}=(3-(-2),1-(-2))\\\\\overrightarrow {DE}=(5,3)\\\\\overrightarrow {EF}=(x_F-x_E,y_F-y_E)\\\\\overrightarrow {EF}=(6-3),-5-1)\\\\\overrightarrow {EF}=(3,-5)\\Hence,\\\\cos\angle E=\frac{5*3+3*(-5)}{\sqrt{34}*\sqrt{34} } \\\\cos\angle E=\frac{15-15}{34 }\\\\cos\angle E=\frac{0}{34 }\\\\cos\angle E=0\\\\m\angle E=90^0\)

Answer:

-3.72

Step-by-step explanation:

5.58+-9

-9+5=-4

-4+.28=-3.72

The approximate size of the cover that Maria will need to buy is 45. 84 square feet

The formula for calculating the circumference of a circle is expressed as;

Circumference = πr²

Where 'r' is the radius of the circle

Now, let's substitute the value of the circumference

24 = 2 × 3. 14 × r

r = 24/6. 28

r = 3. 82 feet

Formula for area = πr²

Substitute value of r

Area = 3. 14 × (3. 82)²

Area = 3. 14 × 14. 59

Area = 45. 84 square feet

Hence, the value is  45. 84 square feet

Learn more about area here:

https://brainly.com/question/25292087

#SPJ1

Answer:

the solution to the system of nonlinear equations is C. (0,3)

12. MATLAB code: `f = (-3*t.^2 + 5*t + 20).*(t < 0) + (3*t.^2 + 5*t).*(t >= 0)`

13. MATLAB function: `function random_values = UniGen(n, a, b); random_values = (b - a) * rand(n, 1) + a; end`

MATLAB code to calculate f(t) using the given equation:

t = -9:0.5:9; % Generate values of t from -9 to 9 in steps of 0.5

f = zeros(size(t)); % Initialize f(t) vector

for i = 1:numel(t)

   if t(i) < 0

       f(i) = -3*t(i)^2 + 5*t(i) + 20;

   else

       f(i) = 3*t(i)^2 + 5*t(i);

   end

end

% Display the results

disp('t    f(t)');

disp('--------');

disp([t' f']);

```

This code generates values of `t` from -9 to 9 in steps of 0.5 and calculates `f(t)` based on the given equation. The results are displayed in a tabular format showing the corresponding values of `t` and `f(t)`.

13. MATLAB function UniGen to generate uniformly distributed random values:

function random_values = UniGen(n, a, b)

   % n: Number of random values to generate

   % a: Start of the interval

   % b: End of the interval

   random_values = (b - a) * rand(n, 1) + a;

end

This MATLAB function named `UniGen` generates `n` random values that are uniformly distributed on the interval `[a, b]`. It utilizes the `rand` function to generate random values between 0 and 1, which are then scaled and shifted to fit within the specified interval `[a, b]`. The generated random values are returned as a column vector.

Learn more about MATLAB code

brainly.com/question/12950689

#SPJ11

A truck's 42-in.-diameter wheels are turning at 505 rpm, the linear speed of the truck is  38.52 mph

The linear speed of the truck in mph, we can use the formula:

Linear Speed = (π * Diameter * RPM) / (12 * 5280),

where Diameter is the diameter of the wheels in inches, RPM is the rotational speed in revolutions per minute, π is the mathematical constant pi, and 12 and 5280 are conversion factors to convert inches to feet and feet to miles, respectively.

The diameter of the truck's wheels is 42 inches and the wheels are turning at 505 rpm, we can substitute these values into the formula to calculate the linear speed.

Linear Speed = (π * 42 * 505) / (12 * 5280).

Evaluating this expression, we find that the linear speed of the truck is approximately 38.52 mph.

Therefore, the main answer is 38.52 mph.

To know more about linear speedrefer here

https://brainly.com/question/30397189#

#SPJ11