simplify (2x^2+3)(x+4
Answers
Answer:
23+32−5+12 is the equaequation simplified
Step-by-step explanation:
Related Questions
Which function has a greater rate of change?
Function A:
x 1.5 2.5 3.5 4.5 5.5
y –5 0 5 10 15
Function B:
y = –4.5x + 15
Function A has a rate change of BLANK and Function B has a rate change of BLANK so Function BLANK has a greater rate of change
Answers
Answer:
5; -4.5; Function AStep-by-step explanation:
Rate of change for function A is:
(15 - 10)/(5.5 - 4.5) = 5/1 = 5Rate of change of function B is:
-4.5 as the slope is the rate of changeComparing the values:
5 > - 4.5Function A has a greater rate of change
Answer:
Answer:
5; -4.5; Function A
Step-by-step explanation:
Rate of change for function A is:
(15 - 10)/(5.5 - 4.5) = 5/1 = 5
Rate of change of function B is:
-4.5 as the slope is the rate of change
Comparing the values:
5 > - 4.5
Function A has a greater rate of change
if you take a random sampling of 100,000 human beings and find that only 1 of them has substituted an a at a location where the other 99,999 have a t, this would be considered a
Answers
If you take a random sampling of 100,000 human beings and find that only 1 of them has substituted an a at a location where the other 99,999 have a t, this would be considered a rare event.
In statistics, when a random sampling of a large population reveals an extremely rare occurrence or outlier, it is considered an unusual event or anomaly.
In the scenario described, where out of 100,000 human beings, only 1 individual has substituted an 'a' at a location where the other 99,999 individuals have a 't', this finding would be considered an extremely rare event.
Such occurrences can raise suspicion and warrant further investigation. It may indicate a potential error or anomaly in the data collection process, genetic mutation, transcription error, or other factors that caused the observed difference.
Statistical analysis can help assess the significance of this occurrence by calculating probabilities, conducting hypothesis tests, or considering the context of the situation.
Additionally, careful examination of the methodology, data collection procedures, and potential sources of bias is necessary to ensure the validity and reliability of the results.
In summary, finding a single individual with a different substitution in a random sampling of 100,000 human beings would be considered an unusual and potentially significant event, prompting further investigation and analysis to understand its underlying causes and implications.
To know more about rare events refer here :
https://brainly.com/question/31392351#
#SPJ11
What is the area of trapezoid ABCD?
Enter your answer as a decimal or whole number in the box. Do
not round at any steps.
units²
-18 -16 -14 -12 -10
D(-13,-11)
-8
-6
A(-1,5)
4
-2
2
0
4
-6
-8
-10
-12
0/2
C (0, -2)
B(3, 2)
4
6
Answers
Given the coordinates above, the area of the trapezoid is approximately 41.
We have,
A trapezoid is a quadrilateral with at least one set of parallel sides in American and Canadian English. A trapezoid is known as a trapezium in British and other varieties of English.
For the calculation showing the above solution:
Step 1 - Given:
A = (-3,2)
B = (1, 5) = ⊥
C = (-7, -3)
D = (0.-2)
Step 2 - To get the distance between the points we need to use the formula for Distance between two points which is given as:
d=√((x2 – x1)² + (y2 – y1)²).
Distance of Line AB =
√((1 – (-3))² + (5 – 2)²).
= √[(4)² + (3)²]
= √( 16 + 9)
= √25
AB= 5
Repeat this for BC, CD, DA and we'd get the following
BC = 11.313708498985
CD = 7.0710678118655
DA = 5
Step 3 - From the above structure, [see attached] we then apply the formula for the area of a Trapezoid (Trapezium) which is given as:
A = [(a+b)/2] h
Where a = 5
b = 11.313708498985
h = 5
= [(5+11.313708498985)/2] 5
= 40.7842712475
= 41
Learn more about Trapezoid:
brainly.com/question/1410008
#SPJ1
complete question:
What is the area of trapezoid ABCD?
Enter your answer as a decimal or whole number in the box. Do not round at any steps.
units²
Trapezoid A B C D on a coordinate plane with vertex A at negative 3 comma 2, vertex B at 1 comma 5, vertex C at negative 7 comma negative 3, and vertex D at 0 comma negative 2. Angle B is shown to be a right angle.
The figure shows two semicircles. Find the area of the shaded part in terms of pi. Please explain in detail thank you!

Answers
Answer: 3pi/2
This is equivalent to 1.5pi
The units for the area are in square centimeters.
===============================================
Work Shown:
The larger semicircle has radius 2 cm.
So r = 2 is plugged into the area of a semicircle formula below
A = (pi*r^2)/2
A = (pi*2^2)/2
A = (4pi)/2
A = 2pi
The area of the larger semicircle is 2pi square cm.
Repeat those steps but now use r = 1. This will compute the area of the unshaded smaller semicircle
A = (pi*r^2)/2
A = (pi*1^2)/2
A = pi/2
The area of the smaller unshaded semicircle is pi/2 square cm.
------------------------
From here, we subtract the two results to get the shaded area:
(larger semicircle area) - (smaller semicircle area) = (2pi) - (pi/2) = 3pi/2
This is equivalent to 1.5pi since 3/2 = 1.5
Find two functions defined implicitly by the given relation y^2-64x^2=64
Answers
Answer: The two functions are
f(x) = sqrt(64x^2+64)
g(x) = -sqrt(64x^2+64)
Graphing these together forms a hyperbola
To get these two functions, we need to solve for y
y^2 - 64x^2 = 64
y^2 = 64x^2 + 64
y = sqrt(64x^2 + 64) or y = -sqrt(64x^2 + 64)
The last line is similar to how x^2 = 9 has two solutions (x = plus or minus 3)
Can someone pls give me the answer to this?
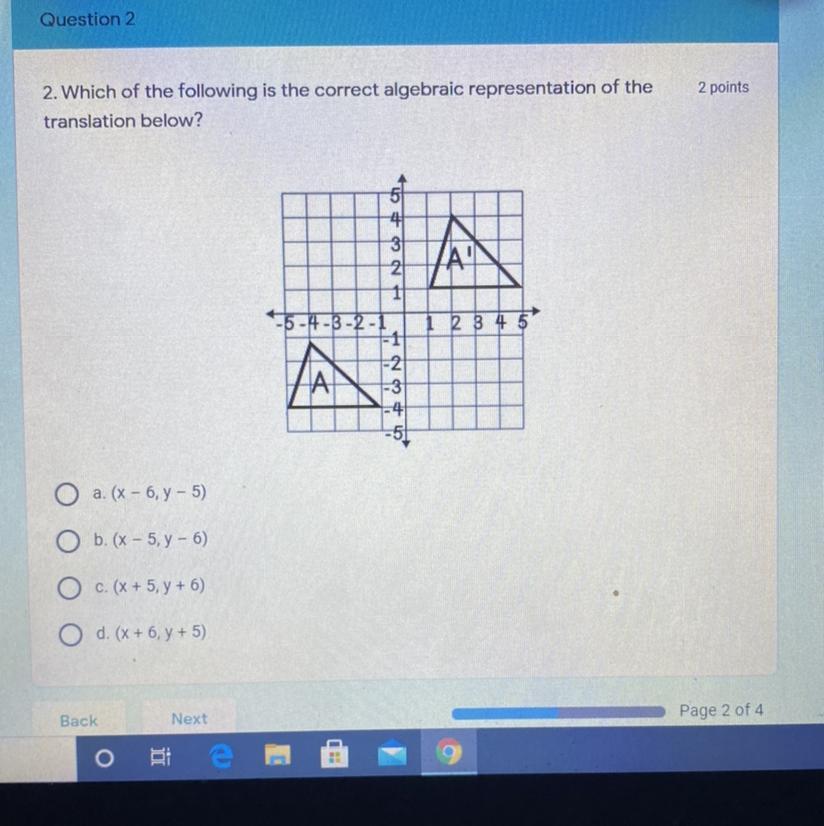
Answers
Answer:
A
Step-by-step explanation:
It went down 5 so y-5 and it also went left 6 so x-6
(x-6,y-5)
I'm pretty sure the top right is before it was moved
Brainliest Appreciated! :)
Answer:
D
Step-by-step explanation:
lets take one point of each triangle
A(-5,-4) A´(1,1)
-5 to 1 is 6
-4 to 1 is 5
( x + 6, y - 5 )
Determine which values in the replacement set make the inequality true.
x-3>12
6,10,14,18
Answers
The replacement set, only \(x = 18\) makes the inequality \(x - 3 > 12\) true. The values \(x = 6\), \(x = 10\), and \(x = 14\) do not satisfy the inequality.
To determine which values in the replacement set make the inequality \(x - 3 > 12\) true, we can substitute each value from the replacement set into the inequality and evaluate whether the inequality holds.
Let's check each value:
1. For \(x = 6\):
Substituting \(x = 6\) into the inequality, we have:
\(6 - 3 > 12\)
\(3 > 12\)
The inequality is not true when \(x = 6\).
2. For \(x = 10\):
Substituting \(x = 10\) into the inequality, we have:
\(10 - 3 > 12\)
\(7 > 12\)
The inequality is not true when \(x = 10\).
3. For \(x = 14\):
Substituting \(x = 14\) into the inequality, we have:
\(14 - 3 > 12\)
\(11 > 12\)
The inequality is not true when \(x = 14\).
4. For \(x = 18\):
Substituting \(x = 18\) into the inequality, we have:
\(18 - 3 > 12\)
\(15 > 12\)
The inequality is true when \(x = 18\).
In summary, out of the values in the replacement set, only \(x = 18\) makes the inequality \(x - 3 > 12\) true. The values \(x = 6\), \(x = 10\), and \(x = 14\) do not satisfy the inequality.
Learn more about inequality here
https://brainly.com/question/30238989
#SPJ11
34.2 million Americans, or 10.5% of the population, had diabetes in the year 2018. What is the probability that a randomly chosen person has diabete
Answers
The probability that a randomly chosen person has diabetes is approximately 10.45%.
The probability that a randomly chosen person has diabetes can be calculated by dividing the number of people with diabetes by the total population. Using the given data, we have:
Total population = 100%Probability of having diabetes = 10.5%Number of people with diabetes = 34.2 million
To find the probability of a randomly chosen person having diabetes, we divide the number of people with diabetes by the total population as follows:
Probability of having diabetes = (Number of people with diabetes / Total population) x 100%
= (34.2 million / 327 million) x 100%
= 0.1045 or 10.45%
Therefore, the probability that a randomly chosen person has diabetes is approximately 10.45%.
Know more about probability here:
https://brainly.com/question/30034780
#SPJ11
{-3,453+5,748} - {8,9703-12,749}
Answers
PLEASE GIVE ME BRAINLIEST!
I hope this helps. thank you and have a good day ;)
Answer:
{6,341}
Step-by-step explanation:
{-3,453+5,748} is the same as 5,748 - 3,453, which is equal to 2,295.{8,9703-12,749} is the same as 8,703 - 12,749, which is equal to -4,046.
{2,295} - {-4,046} = {6,341}
A student mows lawns on the weekends. It takes him 110 minutes to mow 2 lawns. What prediction can you make about the time he will spend this weekend if he has 12 lawns to mow?
It will take him 10 hours to mow 12 lawns.
It will take him 11 hours to mow 12 lawns.
It will take him 17 hours to mow 12 lawns.
It will take him 48 hours to mow 12 lawns.
Answers
The prediction for the weekend is it will take him 11 hours to mow 12 lawns
Given data ,
A student mows lawns on the weekends
It takes him 110 minutes to mow 2 lawns
Now , the time taken for mowing 12 lawns is given by the proportion ,
where 110 / 2 = A / 12
Multiply by 12 on both sides , we get
A = 6 x 110
On further simplification, we get:
A = 660 minutes
On converting 660 minutes to hours
1 hour = 60 minutes
So , 660 minutes = 11 hours
A = 11 hours
Hence , the time taken is 11 hours
To learn more about proportion click :
https://brainly.com/question/7096655
#SPJ1
your investment of 18500 at 17.6% compounded quarterly for 7.5 years will be worth how much ?
Answers
The investment of $18,500 at 17.6% compounded quarterly for 7.5 years will be worth (a future value of) $67,326.60.
What is the future value?The future value is the present value compounded periodically at an interest rate.
Compounding involves computing interest on interest.
The future value of the investment after the stated period can be determined using an online finance calculator as follows:
N (# of periods) = 30 years
I/Y (Interest per year) = 17.6%
PV (Present Value) = $18,500
PMT (Periodic Payment) = $0
Results:
Future Value (FV) = $67,326.60
Total Interest = $48,826.60
Thus, in 7.5 years' time, the investment will be worth $67,326.60.
Learn more about the future value at https://brainly.com/question/24703884
#SPJ1
The z-score for 940 h is -0.98.
Using the answer from Step 1, what percent of these light bulbs
will last at least 940 h?
Answers
Approximately 16.35% of the light bulbs will last at least 940 hours.
To find the percent of light bulbs that will last at least 940 hours, we need to calculate the area under the standard normal distribution curve to the right of the given z-score (-0.98).
Using a standard normal distribution table or a calculator, we can find the corresponding area, which represents the percentage.
The z-score of -0.98 corresponds to a cumulative probability of approximately 0.1635 or 16.35%.
Therefore, approximately 16.35% of the light bulbs will last at least 940 hours.
Learn more about percent here:
https://brainly.com/question/31323953
#SPJ11
Which graph shows an exponential growth function?

Answers
Graph-2 shows an exponential growth function.
Exponential functions are used for many real-world applications such as finance, forensics, computer science, and most of the life sciences. Working with an equation that describes a real-world situation gives us a method for making predictions. Seeing their graphs gives us another layer of insight for predicting future events.
Exponential growth is modeled by functions of form f(x)=b^x where the base is greater than one. Exponential decay occurs when the base is between zero and one. We’ll use the functions f(x)=2^x and g(x)=(1/2)^x to get some insight into the behavior of graphs that model exponential growth and decay. In each table of values below, observe how the output values change as the input increases by 1.
To know more about exponential growth function,
https://brainly.com/question/30607309
Help if you understand thanks sm

Answers
Answer:
Represents decay ( because .72 < 1 )
The amount decreases 72% each 'x' time period
Step-by-step explanation:
What is the slope of a line that goes through the origin and the point (6, -4)?

Answers
The slope of the line that goes through the origin and the point (6, -4) is -2/3.
To find the slope of a line that goes through two given points (x₁, y₁) and (x₂, y₂), you can use the formula:
slope = (y₂ - y₁) / (x₂ - x₁)
In this case, one of the points is the origin, which has coordinates (0, 0), so x₁ = 0 and y₂ = 0. The other point is (6, -4), so x₂ = 6 and y₂ = -4. Substituting these values into the slope formula gives:
slope = (-4 - 0) / (6 - 0) = -4/6 = -2/3
To learn more about slope click on,
https://brainly.com/question/27924340
#SPJ1
Consider the following: x 29 62 75 99 108 y 215 225 173 129 111 1) what is slope of the regression line predicting y from x,rounded to 2 decimal places?
Answers
The slope of the regression line predicting y from x is 0.30.
Given that,
x y
29 215
62 225
75 173
99 129
108 111
So, the coordinate points are (29, 215) and (62, 225)
The formula to find the slope of a line is slope = (y₂-y₁)/(x₂-x₁).
Here, slope = (225-215)/62-29)
= 10/33
= 0.30
Therefore, the slope of the regression line predicting y from x is 0.30.
To learn more about the slope of a line visit:
https://brainly.com/question/14511992.
#SPJ4
midpoint of AB with A(-3, 5) and B(1, 7).
Answers
Answer:
(- 1, 6 )
Step-by-step explanation:
Given endpoints (x₁, y₁ ) and (x₂, y₂ ) then the midpoint is
[ \(\frac{1}{2}\) (x₁ + x₂ ), \(\frac{1}{2}\) (y₁ + y₂ ) ]
Here (x₁, y₁ ) = A(- 3, 5) and (x₂, y₂ ) = B(1, 7) , thus
midpoint = [ \(\frac{1}{2}\) (- 3 + 1 ), \(\frac{1}{2}\) (5 + 7) ] = (- 1, 6 )
The concentration of photons in a uniform light beam with a wavelength of 500 nm is 1.7 x 1013 m-3. The intensity of the beam is: A) 6.7 x 10-6 W/m 2 D) 4.0 103 W/m 2 B) 1.0 x 103 W/m 2 E) 3.2 x 102 W/m 2 C) 2.0 x 103 W/m 2
Answers
The energy of each photon in the beam is given by E = hc/λ, where h is Planck's constant, c is the speed of light, and λ is the wavelength. Substituting the values, we get E = (6.626 x 10^-34 J s)(2.998 x 10^8 m/s)/(500 x 10^-9 m) = 3.98 x 10^-19 J.
The intensity of the beam is the rate at which energy is passing through a unit area perpendicular to the direction of propagation of the beam, given by I = P/A, where P is the power and A is the area. The power of the beam is the product of the energy of each photon and the number of photons passing through a unit area per unit time, given by P = nEAv, where n is the concentration of photons, A is the area, v is the speed of the beam, and E is the energy of each photon.
Substituting the values, we get P = (1.7 x 10^13 m^-3)(3.98 x 10^-19 J/photon)(1 m^2/s)(2.998 x 10^8 m/s) = 1.02 W. The area of the beam is not given, so we cannot calculate the intensity directly. However, if we assume a circular beam with a radius of 1 cm (area = πr^2 = π(0.01 m)^2 = 3.14 x 10^-4 m^2), we can calculate the intensity as I = P/A = 1.02 W/3.14 x 10^-4 m^2 = 3.24 x 10^3 W/m^2, which is closest to option E) 3.2 x 10^2 W/m^2 (after rounding to the nearest tenth).
Learn more about photon here:
https://brainly.com/question/28134171
#SPJ11
Please help me I need this answer

Answers
The feature that will be the same as the original is:
The perimeter is the same.
The coordinate of C' is (3, 4).
The slope of A'C' is 1/4.
We have,
To rotate a point 180 degrees clockwise around another point, you can follow these steps:
- Calculate the displacement vector from the center of rotation to the point you want to rotate.
- Reverse the direction of the displacement vector.
- Apply the reversed displacement vector to the center of rotation.
- Let's apply these steps to each vertex of triangle ABC to find the coordinates of A', B', and C'.
So,
- Coordinate of A' (rotated point of A around (3, 4)):
Displacement vector: (A' - Center of rotation) = (A - Center of rotation) = (-5, 2) - (3, 4) = (-8, -2).
Reverse the direction of the displacement vector:
Reversed displacement vector: (-8, -2) * (-1) = (8, 2).
Apply the reversed displacement vector to the center of rotation:
Coordinate of A': (3, 4) + (8, 2) = (11, 6).
- Coordinate of B' (rotated point of B around (3, 4)):
Displacement vector: (B' - Center of rotation) = (B - Center of rotation) = (-2, 5) - (3, 4) = (-5, 1).
Reverse the direction of the displacement vector:
Reversed displacement vector: (-5, 1) * (-1) = (5, -1).
Apply the reversed displacement vector to the center of rotation:
Coordinate of B': (3, 4) + (5, -1) = (8, 3).
- Coordinate of C' (rotated point of C around (3, 4)):
Displacement vector: (C' - Center of rotation) = (C - Center of rotation) = (3, 4) - (3, 4) = (0, 0).
Reverse the direction of the displacement vector:
Reversed displacement vector: (0, 0) * (-1) = (0, 0).
Apply the reversed displacement vector to the center of rotation:
Coordinate of C': (3, 4) + (0, 0) = (3, 4).
So,
The coordinate of A' is (11, 6).
The coordinate of B' is (8, 3).
The coordinate of C' is (3, 4).
To find the perimeter and area of a triangle, we can use the coordinates of its vertices.
Let's start by finding the perimeter and area of triangle ABC.
Triangle ABC:
A = (-5, 2)
B = (-2, 5)
C = (3, 4)
The perimeter of triangle ABC:
The perimeter of a triangle is the sum of the lengths of its sides. We can use the distance formula to calculate the lengths of each side and then sum them up.
Length of side AB:
\(d_{AB} = \sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)\)
= √((-2 - (-5))² + (5 - 2)²)
= √(3² + 3²)
= √(18)
= 3√2
Length of side BC:
\(d_{BC} = \sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)\)
= √((3 - (-2))² + (4 - 5)²)
= √(5² + 1²)
= √(26)
Length of side CA:
\(d_{CA}= \sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)\)
= √((-5 - 3)² + (2 - 4)²)
= √((-8)² + (-2)²)
= √(64 + 4)
= √(68)
= 2√17
The perimeter of triangle ABC:
\(P_{ABC} = d_{AB} + d_{BC} + d_{CA}\)
= 3√2 + √26 + 2√17
Area of triangle ABC:
The area of a triangle can be calculated using the coordinates of its vertices with the Shoelace formula.
Area of triangle ABC:
A_ABC = 1/2 x |(x1 x y2 + x2 x y3 + x3 x y1) - (y1 x x2 + y2 x x3 + y3 x x1)|
= 1/2 x |((-5 x 5) + (-2 x 4) + (3 x 2)) - ((2 x -2) + (5 x 3) + (4 x -5))|
= 1/2 x |(-25 - 8 + 6) - (-4 + 15 - 20)|
= 1/2 x |-27 - (-9)|
= 1/2 x |-27 + 9|
= 1/2 x |-18|
= 9
Now let's find the perimeter and area of triangle A'B'C', which is the rotated triangle of ABC.
Triangle A'B'C':
A' = (11, 6)
B' = (8, 3)
C' = (3, 4)
The perimeter of triangle A'B'C':
Using the same approach as before, we calculate the lengths of the sides:
Length of side A'B':
d_A'B' = √((x2 - x1)^2 + (y2 - y1)^2)
= √((8 - 11)^2 + (3 - 6)^2)
= √((-3)^2 + (-3)^2)
= √(18)
= 3√2
Length of side B'C':
d_B'C' = √((x2 - x1)^2 + (y2 - y1)^2)
= √((3 - 8)^2 + (4 - 3)^2)
= √((-5)^2 + 1^2)
= √(26)
Length of side C'A':
d_C'A' = √((x2 - x1)^2 + (y2 - y1)^2)
= √((3 - 11)^2 + (4 - 6)^2)
= √((-8)^2 + (-2)^2)
= √(68)
= 2√17
The perimeter of triangle A'B'C':
P_A'B'C' = d_A'B' + d_B'C' + d_C'A'
= 3√2 + √26 + 2√17
Area of triangle A'B'C':
Using the same Shoelace formula as before:
Area of triangle A'B'C':
A_A'B'C' = 1/2 x |(x1 x y2 + x2 x y3 + x3 x y1) - (y1 x x2 + y2 x x3 + y3 x x1)|
= 1/2 x |((11 x 3) + (8 x 4) + (3 x 6)) - ((6 x 8) + (3 x 3) + (4 x 11))|
= 1/2 x |(33 + 32 + 18) - (48 + 9 + 44)|
= 1/2 x |(83) - (101)|
= 1/2 x |-18|
= 9
Now,
The perimeter of triangle ABC is 3√2 + √26 + 2√17, and the area of triangle ABC is 9.
The perimeter of triangle A'B'C' is 3√2 + √26 + 2√17, and the area of triangle A'B'C' is 9.
The slope of A'C' can be calculated using the coordinates of A' and C'.
The slope of a line can be calculated using the formula:
slope = (y2 - y1) / (x2 - x1)
For A'(11, 6) and C'(3, 4), the slope of A'C' is:
slope = (4 - 6) / (3 - 11)
= -2 / -8
= 1/4
Thus,
The feature that will be the same as the original is:
The perimeter is the same.
The coordinate of C' is (3, 4).
The slope of A'C' is 1/4.
Learn more about coordinates here:
https://brainly.com/question/13118993
#SPJ1
What is the slope of the line?
A.) 1
B.) 1/2
C.) -2
D.) 2

Answers
Answer:
D
Step-by-step explanation:
M is a point on line segment LH. KM is a line segment. Select all the equations that represent the relationship between the measures of the angles in the figure.
Group of answer choices a = b a + b = 90 b = 90 − a a + b =180 180 − a = b 180 = b − a
Answers
Answer:
180 - a = b and a + b = 180
Step-by-step explanation:
Two similar circles are shown. The circumference of the
larger circle, with radius OB, is 3 times the
circumference of the smaller circle, with radius OA.
Radius OB measures x units. Which expression
represents the circumference of the smaller circle with
radius OA?
A.(pi/3) x units
B.(2pi/3) x units
C.2pi x units
D.6pi x units

Answers
Answer:
(B). \(\frac{2\pi }{3} x\)
Step-by-step explanation:

Which of the following number lines shows the solution to the compound inequality given below?
-2<3r+4<13

Answers
Answer:
We get -2 < r < 3
Corresponding to the fourth choice
The fourth number line is the correct option
Step-by-step explanation:
-2 < 3r+4 < 13
We have to isolate r,
subtracting 4 from each term,
-2-4< 3r + 4 - 4 < 13 - 4
-6 < 3r < 9
divding each term by 3,
-6/3 < r < 9/3
-2 < r < 3
so, the interval is (-2,3)
or, -2 < r < 3
this corresponds to
The fourth choice (since there is no equality sign)
Find two power series solutions of the given differential equation about the ordinary point x = 0. y'' + xy = 0
Answers
Answer:
First we write y and its derivatives as power series:
y=∑n=0∞anxn⟹y′=∑n=1∞nanxn−1⟹y′′=∑n=2∞n(n−1)anxn−2
Next, plug into differential equation:
(x+2)y′′+xy′−y=0
(x+2)∑n=2∞n(n−1)anxn−2+x∑n=1∞nanxn−1−∑n=0∞anxn=0
x∑n=2∞n(n−1)anxn−2+2∑n=2∞n(n−1)anxn−2+x∑n=1∞nanxn−1−∑n=0∞anxn=0
Move constants inside of summations:
∑n=2∞x⋅n(n−1)anxn−2+∑n=2∞2⋅n(n−1)anxn−2+∑n=1∞x⋅nanxn−1−∑n=0∞anxn=0
∑n=2∞n(n−1)anxn−1+∑n=2∞2n(n−1)anxn−2+∑n=1∞nanxn−∑n=0∞anxn=0
Change limits so that the exponents for x are the same in each summation:
∑n=1∞(n+1)nan+1xn+∑n=0∞2(n+2)(n+1)an+2xn+∑n=1∞nanxn−∑n=0∞anxn=0
Pull out any terms from sums, so that each sum starts at same lower limit (n=1)
∑n=1∞(n+1)nan+1xn+4a2+∑n=1∞2(n+2)(n+1)an+2xn+∑n=1∞nanxn−a0−∑n=1∞anxn=0
Combine all sums into a single sum:
4a2−a0+∑n=1∞(2(n+2)(n+1)an+2+(n+1)nan+1+(n−1)an)xn=0
Now we must set each coefficient, including constant term =0 :
4a2−a0=0⟹4a2=a0
2(n+2)(n+1)an+2+(n+1)nan+1+(n−1)an=0
We would usually let a0 and a1 be arbitrary constants. Then all other constants can be expressed in terms of these two constants, giving us two linearly independent solutions. However, since a0=4a2 , I’ll choose a1 and a2 as the two arbitrary constants. We can still express all other constants in terms of a1 and/or a2 .
an+2=−(n+1)nan+1+(n−1)an2(n+2)(n+1)
a3=−(2⋅1)a2+0a12(3⋅2)=−16a2=−13!a2
a4=−(3⋅2)a3+1a22(4⋅3)=0=04!a2
a5=−(4⋅3)a4+2a32(5⋅4)=15!a2
a6=−(5⋅4)a5+3a42(6⋅5)=−26!a2
We see a pattern emerging here:
an=(−1)(n+1)n−4n!a2
This can be proven by mathematical induction. In fact, this is true for all n≥0 , except for n=1 , since a1 is an arbitrary constant independent of a0 (and therefore independent of a2 ).
Plugging back into original power series for y , we get:
y=a0+a1x+a2x2+a3x3+a4x4+a5x5+⋯
y=4a2+a1x+a2x2−13!a2x3+04!a2x4+15!a2x5−⋯
y=a1x+a2(4+x2−13!x3+04!x4+15!x5−⋯)
Notice that the expression following constant a2 is =4+ a power series (starting at n=2 ). However, if we had the appropriate x -term, we would have a power series starting at n=0 . Since the other independent solution is simply y1=x, then we can let a1=c1−3c2, a2=c2 , and we get:
y=(c1−3c2)x+c2(4+x2−13!x3+04!x4+15!x5−⋯)
y=c1x+c2(4−3x+x2−13!x3+04!x4+15!x5−⋯)
y=c1x+c2(−0−40!+0−31!x−2−42!x2+3−43!x3−4−44!x4+5−45!x5−⋯)
y=c1x+c2∑n=0∞(−1)n+1n−4n!xn
Learn more about constants here:
https://brainly.com/question/11443401
#SPJ4
Light travels about `180000000` kilometers in `10` minutes.
How many kilometers per second?
How many kilometers per minute?
How many kilometer can light travel in 7 minutes? Im not even gonna say anything..
Answers
Answer:
300000 km per second
18000000 km per minute
126000000 km in 7 minutes
Step-by-step explanation:
In 10 minutes there are (10*60) seconds, which is 600 seconds.
180000000/600 = 300000
To find km per minute,
180000000/10 = 18000000
To find km in 7 minutes,
18000000*7=126000000
Light travels 18000000 kilometers per minute and 300000 kilometers per second.
What is the unitary method?The unitary method is a technique for solving a problem by first finding the value of a single unit, and then finding the necessary value by multiplying the single unit value.
Given that, light travels about 180000000 kilometers in 10 minutes.
A) We know that, 1 minute =60 seconds
10 minutes =600 seconds
Now, number of kilometers per second
= 180000000/600
= 300000 kilometers/second
B) Number of kilometers per minute
= 180000000/10
= 18000000 kilometers per minute
C) Number of kilometer light travel in 7 minutes
= 18000000×7
= 126000000
Therefore, light travels 18000000 kilometers per minute and 300000 kilometers per second.
To learn more about the unitary method visit:
brainly.com/question/22056199.
#SPJ5
What is the solution set of |-x| = -10?
(10)
7-10)
{-10, 10)
no solution
Answers
Answer:
{-10, 10)
Step-by-step explanation:
| | - means to only take the number inside, not the sign
x=-10 or 10
Answer:
i dont understand what you want me to answer
Step-by-step explanation:
pls help Explain how to change the base of log5 x into a natural logarithm.
Answers
㏒₅x in Natural logarithm is \(\frac{lnx}{ln5}\).
What are Natural logarithms?The base-e logarithm of an integer x, where e is a mathematical constant roughly equal to 2.718, is the natural logarithm of that number. Instead of the expected abbreviated notation ㏒ex, it is typically written using ㏑x. A natural logarithm can be expressed in exponential form as follows:
㏑x=a⇒\(x=e^a\)
Natural logarithm, is like a normal logarithm it follows all the basic algebraic laws, like addition, subtraction, multiplication of logarithms.
The natural logarithm follows the same as common logarithms of base 10. That is, \(ln (ab) = ln a + ln b\); \(ln (\frac{a}{b} ) = lna-lnb\); The natural logarithm and the common logarithm are related through
㏒₅x=\(\frac{logx}{log5}\);
\(\frac{logx}{log5} *\frac{lne}{lne} ;\\\frac{logx}{lne} *\frac{lne}{log5} ;\\\)
㏑x×(\(\frac{1}{ln5}\));
⇒\(\frac{lnx}{ln5}\).
㏒₅x in Natural logarithm is \(\frac{lnx}{ln5}\).
To refer more about Natural logarithms, visit:
https://brainly.com/question/29373904
#SPJ1
Alonzo is making apple tarts for a party. He needs 3 apples for every 8
tarts. How many apples does he need if he wants to make 40 tarts?
(A) 18 apples
(B) 15 apples
(C) 12 apples
(D) 10 apples
Answers
Answer:
15
Step-by-step explanation:
so the amount for apples are 3 for 8.so if you multiply 8 x 5 it is 40.3 is for 8 and there is the answer
suppose you obtain a chi-square statistic of 3.86. are your results statistically significant if the critical value obtained from the distribution of chi-square is 6.63 with an alpha level of .01?
Answers
The chi-square statistic of 3.86 is not statistically significant if the critical value obtained from the distribution of chi-square is 6.63 with an alpha level of .01.
To determine if the obtained chi-square statistic of 3.86 is statistically significant or not, we need to compare it to the critical value obtained from the distribution of chi-square, which is 6.63, at a significance level of 0.01.
In this case, the obtained chi-square value is less than the critical value, indicating that we fail to reject the null hypothesis. This means that the observed frequencies in the sample are not significantly different from the expected frequencies based on the null hypothesis. The alpha level of 0.01 indicates that we are willing to accept a 1% chance of making a Type I error, which is rejecting the null hypothesis when it is actually true. Since the obtained chi-square value is not greater than the critical value, we do not have sufficient evidence to reject the null hypothesis.
In summary, the results are not statistically significant at the 0.01 significance level, based on the obtained chi-square statistic of 3.86 and the critical value of 6.63. This means that there is no significant difference between the observed and expected frequencies, based on the null hypothesis.
Know more about Chi-square here :
https://brainly.com/question/4543358
#SPJ11
Can you please help meeeee!!!!!!!!!!!

Answers
Answer:
90 - 5 = 85/2 = 42.5 degrees
Answer:
90 - 5 = 85/2 = 42.5 degrees
Step-by-step explanation:
Hope i helped i tried :3 <3