Answers
Answer:
a)-27/20
Step-by-step explanation:
3/5 ÷ (-4/9)
3/5 × (-9/4)
-27/20
Hope it will help
Related Questions
Elena's aunt bought her a $200 savings bond when she was born. When Elena is 20 years old, the bond will have earned 110% in interest. How much will the bond be worth when Elena is 20 years old? Dhoma
Answers
Step-by-step explanation:
$157.50
i HOPE THIS HELP YOU
Question 6 (9 points) At CJ's Diner, there are three sizes of coffee drinks: regular (300 mL), large (500 mL) and extra large (800 mL), and they cost $2.25, $3.25 and $5.75, respectively. On a particular afternoon, the diner sold a total of 37 coffees. The total volume of coffee sold was 19,100 mL and the amount of money made in coffee sales was $133.25. How many of each size of drink did customers buy that afternoon? Regular:Large:Extra Large:
Answers
regular (r)
Large (l)
ExtraLarge (e)
\(300r+500l+800e=19100\text{ }\)this is the equation 1
the equation 2:
\(2.25r+3.25l+5.75e=133.25\)the equation 3:
\(r+l+e=37\)\(\begin{bmatrix}{300} & {500} & {800} \\ {2.25} & {3.25} & {5.75} \\ {1} & {1} & {1}\end{bmatrix}=\begin{bmatrix}{19100} & {} & {} \\ {133.25} & {} & \\ {37} & & \end{bmatrix}\)r=12
l=15
e=10
According to a survey, 74% of households said that they have never purchased organic fruits or vegetables. Suppose that this result is true for the current population of households. a. Let x be a binomial random variable that denotes the number of households in a random sample of 10 who have never purchased organic fruits or vegetables. What are the possible values that x can assume
Answers
Complete Question
According to a survey, 74% of households said that they have never purchased organic fruits or vegetables. Suppose that this result is true for the current population of households. a. Let x be a binomial random variable that denotes the number of households in a random sample of 10 who have never purchased organic fruits or vegetables. What are the possible values that x can assume? Integers to . b. Find to 3 decimal places the probability that exactly 6 households in a random sample of 10 will say that they have never purchased organic fruits or vegetables. Use the binomial probability distribution formula. Probability
Answer:
a
The possible value of x is 0, 1 ,2,3,4,5,6,7,8,9,10
b
\(P(X = 6) = 0.158 \)
Step-by-step explanation:
From the question we are told that
The proportion that stated that they have not purchased organic fruits or vegetables is \(p =0.74\)
The sample size is n = 10
The possible value x can take is 0, 1 ,2,3,4,5,6,7,8,9,10
Generally the probability that exactly 6 households in a random sample of 10 will say that they have never purchased organic fruits or vegetables is mathematically represented as
\(P(X = 6) = ^nC_6 * p^{6}* (1-p)^{n-6}\)
Here C denotes combination
So
\(P(X = 6) = ^{10}6 * (0.74)^{6}* (1-0.74)^{10-6}\)
=> \(P(X = 6) = 0.158 \)
K.Brew sells a wide variety of outdoor equipment and clothing. The company sells both through mail order and via the internet. Random samples of sales receipts were studied for mail-order sales and internet sales, with the total purchase being recorded for each sale. A random sample of 18 sales receipts for mail-order sales results in a mean sale amount of $74.90 with a standard deviation of $21.75. A random sample of 9 sales receipts for internet sales results in a mean sale amount of $87.30 with a standard deviation of $19.75. Using this data, find the 95% confidence interval for the true mean difference between the mean amount of mail-order purchases and the mean amount of internet purchases. Assume that the population variances are not equal and that the two populations are normally distributed.
Step 1 of 3: Find the point estimate that should be used in constructing the confidence interval.
Step 2 of 3: Find the margin of error to be used in constructing the confidence interval. Round your answer to six decimal places.
Step 3 of 3: Construct the 95% confidence interval. Round your answers to two decimal places.
Answers
Answer:
Step-by-step explanation:
Step 1. The point estimate is the difference between the the mean amount of mail-order purchases and the mean amount of internet purchases. It becomes
74.9 - 87.3 = - 12.4
Step 2. The formula for determining margin of error is expressed aa
Margin of error = z√(s1²/n1 + s2²/n2)
Where
z = z score
s1 = sample standard deviation for data 1
s2 = sample standard deviation for data 2
n1 = number of samples in group 1
n2 = number of samples in group 2
For a 95% confidence interval, the z score is 1.96
From the information given,
s1 = 21.75
n1 = 18
s2 = 19.75
n2 = 9
z√(s1²/n1 + s2²/n2) = 1.96√(21.75²/18 + 19.75²/9) = 1.96 × 8.343
= 16.35
Step 3. Confidence interval = (x1 - x2) ± z√(s²/n1 + s2²/n2)
95% Confidence interval = - 12.4 ± 16.35
The rate constant for first-order degradation of a N2O2 in a solution (1.0 mg/ml) at 40°C
is 0.00351 hr-1, activation energy is 2000 cal/mol, and R = 1.987 cal/mol/degree.
Calculate
a. The rate constant for first-order degradation of N2O2 at room temperature (25°C).
Answers
The 0.0035 hr⁻¹ first-order degradation rate constant in the 40 °C, 1.0 mg/ml solution, where R = 1.987 cal/mol/degree and 2,000 cal/mol activation energy indicates;
a. The rate constant for first-order degradation of N₂O₂ at room temperature is approximately 4.12595 × 10⁻² hr⁻¹
What is a first-order reaction?A first order reaction is one that has a rate that varies linearly with the concentration of one reactant
The given parameters are;
Temperature of the solution = 40°C
T₁ = 40 °C + 273.15 = 313.15 K
The rate constant, K₁ = 0.00351 hr⁻¹
Concentration of the solution = 1.0 mg/ml
Activation energy, Eₐ = 2000 Cal/mol
R = 1.987 cal/mol/degree
The formula by which the rate constant can be found is presented as follows;
\(log\dfrac{k_2}{k_1} =\dfrac{E_a}{2.303\times R} \times \dfrac{T_2-T_1}{T_1\cdot T_2}\)
a. Room temperature = 25 °C
T₂ = 25 °C + 273.15 = 298.15 K
Therefore;
\(log\dfrac{k_2}{0.00351} =\dfrac{2000}{2.303\times 1.987} \times \dfrac{313.15-298.15}{313.15 \times 298.15}\)
\(k_2=0.00351 \times 10^{\left(\dfrac{2000}{2.303\times 1.987} \times \dfrac{313.15-298.15}{313.15 \times 298.15}\right)} \approx 4.12595\times 10^{-2}\)
The rate constant for first-order degradation of N₂O₂ at room temperature is k₂ ≈ 4.12595 × 10⁻² hr⁻¹Learn more about the rate constant for first-order degradation here:
https://brainly.com/question/14595397
#SPJ1
During your journey, you develop an abscessed tooth and have to visit the dentist. You are prescribed an antibiotic with a dosage of 7.5 mg/kg every six hours. If you weigh 128 pounds and the antibiotic comes in 250 mg tablets, how many tablets should you take each day?
Answers
Answer:
I should take 10.44 tablets in a day, approximately 10.5 tablets.
Step-by-step explanation:
In order to solve this problem we need to convert the weight from pounds to kilograms, to do that we need to divide it by 2.205.
\(w = \frac{128}{2.205}\\w = 58.05 \text{ kg}\)
Since I need to take 7.5 mg per kg of body weight, then in order to find the dosage we need to multiply the weight in kg by 7.5.
\(\text{dosage} = 58*7.5 = 435 \text{ mg}\)
Since I need to take it every six hours and there are 24 hours in a day, we will have to take 4 dosages in a day, therefore we need:
\(\text{dosage(day)} = 435*6 = 2,610 \text{ mg}\)
The antibiotic comes in 250 mg in tablets, therefore the number of tablets is:
\(tablets = \frac{2610}{250} = 10.44\)
I should take 10.44 tablets in a day, approximately 10.5 tablets.
. Find the general solution to
d²y/dx²= 49y. Enter your answer as an equation y = ..
Note: d²y/dx²=k^2y

Answers
The given differential equation is linear with constant coefficients,
\(\dfrac{d^2y}{dx^2} - 49y = 0\)
with characteristic equation
\(r^2 - 49 = 0\)
and hence characteristic roots \(r=\pm7\). This means the general solution to the ODE is
\(y = C_1 e^{7x} + C_2 e^{-7x}\)
In fact, you're given the solution already,
\(y = C_1 e^{kx} + C_2 e^{-kx}\)
and you've determined that
\(\dfrac{d^2y}{dx^2} = k^2 (C_1 e^{kx} + C_2 e^{-kx}) = k^2 y\)
Comparing this to the given ODE, it's obvious that \(k=7\), so you can just replace \(k\) with 7 in the given template solution.
Tutu and Pete go hiking. Tutu brings 7/10 liter of water. Pete brings 500 millimeters of water. How many more millimeters of water did tutu bring than Pete?
Answers
━━━━━━━━━━━━━━━ ♡ ━━━━━━━━━━━━━━━
1 liter of water equals 1000 milliliters.
To find who has more water, you need to convert (the unit) of each person to either liters or milliliters.
Since it asks for millimeters, I'm going to convert Tutu's 7/10 liters to milliliters. Since there are 1000 milliliters in every liter, you have to multiply 7/10 by 1000. 7/10 multiplied by 1000 is 700.
So Pete has 500 milliliters of water and Tutu has 700 milliliters of water.
Now you need to find the difference of 700 and 500 by subtracting.
700-500=200
Tutu bought 200 more milliliters of water than Pete.
━━━━━━━━━━━━━━━ ♡ ━━━━━━━━━━━━━━━
What is another name for Angle 2? Lines E H and D F intersect at point G. Angle 2 is formed by line segments D G and G E and angle 1 is formed by line segments E G and G F. Angle D G E Angle G E D Angle E G F Angle G E F
Answers
When two straight lines or rays intersect at a shared endpoint, an angle is generated. The correct option is A.
What is an angle?When two straight lines or rays intersect at a shared endpoint, an angle is generated. An angle's vertex is the common point of contact. Angle is derived from the Latin word angulus, which means "corner."
The diagram for the given problem can be made as shown below. Therefore, the other name for angle 2 will be ∠DGE.
Hence, the correct option is A.
Learn more about Angle:
https://brainly.com/question/7116550
#SPJ1

Answer:
a
Step-by-step explanation:
got it right
A rectangular picture is twice as long as it is wide. If the
area of the picture is 288 in^2, what are its dimensions?
The dimensions of the picture are_____ in long by_____ in wide.
Answers
Answer:
24 in long by 12 in wide.
Step-by-step explanation:
l=2w
288=(2w)×w
288=2w^2
144=w^2
12=w
width is 12 inches. Plug that in to find length...
l=2×12
l=24
y = -3x + 6
Slope:
y-intercept:
y = 4/3x - 1
Slope:
y-intercept:
y = -1/5x + 3
Slope:
y-intercept:
Answers
Answer:
Step-by-step explanation:
y = mx + c
Slope = m
y-intercept = c
1) y = -3x + 6
Slope = -3
y-intercept = 6
2) y = 4/3 x - 1
Slope = 4/3
y-intercept = -1
3) y = -1/5x+3
Slope = -1/5
y-intercept = 3
Answer:
Step-by-step explanation:
y= -3x +6 \(y=\frac{4}{3} x-1\)
slope: -3 slope=4/3x
y-intercept: (0,6) y-intercept:(0,-1)
\(y=-\frac{1}{5} x+3\)
slope: -1/5x
y-intercept: (0,3)
compare1/2 with 3/4 using (<>=)
Answers
Answer: 3/4 is greater than 1/2
>
Step-by-step explanation:
The data below represents the relationship between the number of incidences of UFO sightings in late 1930s and early 1940s. Draw a scatter plot for the data.
Year of Incidence
1936
1937
1938
1939
1940
1941
1942
1943
1944
1945
1946
Number of Incidences (percent)
0.9
0.8
0.8
1.3
1.4
1.2
1.7
1.8
1.6
1.5
1.5
a.
A graph has years of incidence on the x-axis from 1932 to 1948, and incidence on the y-axis, from 0 to 10. Points are around (1936, 0.9), (1937, 0.8), (1938, 0.8), (1939, 1.3), (1940, 1.4), (1941, 1.2), (1942, 1.7), (1943, 1.8), (1944, 1.6), (1945, 1.5), (1946, 1.5).
c.
A graph has years of incidence on the x-axis from 1932 to 1948, and incidence on the y-axis, from 0 to 10. Points are around (1936, 0.9), (1937, 0.8), (1938, 0.8), (1939, 1.3), (1940, 1.4), (1941, 1.2), (1942, 1.7), (1943, 1.8), (1944, 1.6), (1945, 1.5).
b.
A graph has years of incidence on the x-axis from 1932 to 1948, and incidence on the y-axis, from 0 to 10. Points are around (1936, 0.9), (1937, 1.7), (1938, 0.8), (1939, 1.3), (1940, 1.4), (1941, 1.2), (1942, 1.7), (1943, 1.8), (1944, 1.6), (1945, 1.5), (1946, 1.5).
d.
A graph has years of incidence on the x-axis from 1932 to 1948, and incidence on the y-axis, from 0 to 10. Points are around (1936, 0.9), (1937, 0.8), (1939, 1.3), (1940, 1.4), (1941, 1.2), (1942, 1.7), (1943, 1.8), (1944, 1.6), (1945, 1.5), (1946, 1.5).
Answers
The description of graph of the data about relationship of UFO sightings in late 1930s and early 1940s will be :A graph has years of incidence on the x-axis from 1932 to 1948, and incidence on the y-axis, from 0 to 10. Points are around (1936, 0.9), (1937, 0.8), (1938, 0.8), (1939, 1.3), (1940, 1.4), (1941, 1.2), (1942, 1.7), (1943, 1.8), (1944, 1.6), (1945, 1.5), (1946, 1.5).
Given:
Year of incidence percent
1936 0.9
1937 0.8
1938 0.8
1939 1.3
1940 1.4
1941 1.2
1942 1.7
1943 1.8
1944 1.6
1945 1.5
1946 1.5
We have been given the percentages of different years. The points will be (1936,0.9) , (1937,0.8) , (1938,0.8) , (1939,1.3) , (1940,1.4) , (1941,1.2) , (1942,1.7), (1943,1.8) , (1944,1.6) , (1945,1.5) , (1946,1.5).
We have to just plot the points on the graph to find scatter plot. It is called scatter plot as the points are not in line but they are scattered.
Learn more about graph at https://brainly.com/question/4025726
#SPJ10

please help!!!! need by tomorrow!!

Answers
Answer:
Step-by-step explanation:
Instructions: Use the ratio of a 30-60-90 triangle to solve for the variables. Leave your answers as radicals in simplest form.
If you are using a screen-reader, please consult your instructor for assistance.
x=
y=
Answers
Using the ratio of the sides, we have:$x\sqrt{3} = 12\sqrt{3}$ (opposite the $60^{\circ}$ angle is 12$\sqrt{3}$)$x = 2\sqrt{3}\cdot6$ (the hypotenuse is $2x = 12\sqrt{3}$)Simplifying, we have:$x = 12\sqrt{3}$. Therefore $x=y=12\sqrt{3}$, which is our answer
In a 30-60-90 triangle, the sides have the ratio of $1: \sqrt{3}: 2$. Let's apply this to solve for the variables in the given problem.
Instructions: Use the ratio of a 30-60-90 triangle to solve for the variables. Leave your answers as radicals in simplest form. x=y=Let's first find the ratio of the sides in a 30-60-90 triangle.
Since the hypotenuse is always twice as long as the shorter leg, we can let $x$ be the shorter leg and $2x$ be the hypotenuse.
Thus, we have: Shorter leg: $x$Opposite the $60^{\circ}$ angle: $x\sqrt{3}$ Hypotenuse: $2x$
Now, let's apply this ratio to solve for the variables in the given problem. We know that $x = y$ since they are equal in the problem.
Using the ratio of the sides, we have:$x\sqrt{3} = 12\sqrt{3}$ (opposite the $60^{\circ}$ angle is 12$\sqrt{3}$)$x = 2\sqrt{3}\cdot6$ (the hypotenuse is $2x = 12\sqrt{3}$)Simplifying, we have:$x = 12\sqrt{3}$
Therefore, $x=y=12\sqrt{3}$, which is our answer.
For more such questions on ratio of the sides
https://brainly.com/question/31529028
#SPJ8
What is the surface area of the sphere shown below with a radius of 7?
1
7
A. 49, sq. units
B. 65 sq. units
C. 196 sq. units
D. 457 sq. units
SUBMIT

Answers
Answer:
c
Step-by-step explanation:
the surface area for spheres is
4 × π × r²
4 × π × (7²) = 196 π
HELP I HAVE 3 minutes left

Answers
Answer:
The answer is C
Step-by-step explanation:
it
is
the
answer
C
Which box plot shows data that is skewed right?

Answers
Answer:
I think its a
Step-by-step explanation:
The box plot in option A is right-skewed or in other words positively skewed.
A box plot is a graphical representation of the distribution of a dataset, particularly picturizing its center, spread, and potential outliers. It is also used to find the skewness in the distribution.
It is also known as a box-and-whisker plot.
The given data points are 10, 20, 30, 40, 50, 60.
As the number of observations, n = 6, is even, the following formula will be used to find the median:
\(Med(X) = \dfrac{X_\frac{n}{2}+X_\frac{n}{2} _+_1 }{2}\),
where X is the random variable such that X ∈ [10, 60].
\(X_\frac{n}{2} = X_\frac{6}{2} = X_3 = 30\\X_\frac{n}{2}_+_1 = X_\frac{6}{2}_+_1 =X_{3+1} = X_4 = 40\)
\(Med(X) = \dfrac{30 + 40 }{2}\)
\(= \dfrac{70}{2} \\= 35\)
It is clear that the whiskers of the box plot in Figure A are shifted right to the median, 35.
Thus, the box plot in option A is right-skewed.
Learn more about Box Plot here:
https://brainly.com/question/9827993
#SPJ4
PLEASE HELP ME WITH THIS ONE MATH QUESTION

Answers
The transformation undergone by the function is:
A reflection over the x-axis and a shift of the function by 2 units to the right
What is the transformation of the function?There are different types of transformation such as:
Translation
Reflection
Rotation
Dilation
Now, the transformation rule when a function has a reflection over the x -axis is (x,y) → (x,−y) .
Since f(x) became negative, then we can say there was a reflection over the x-axis.
Now, we see it was subtracted by 2 which indicates a shift of the function by 2 units to the right
Read more about function transformation at: https://brainly.com/question/4289712
#SPJ1
1. A target is divided into 100 squares colored in dark blue, white, and light blue. Amber throws a beanbag that lands on the target.
co
9 25
dark blue
What is the probability that it will land on a dark blue square?
26
white
light blue

Answers
The probability of landing on the dark blue target is 2/5.
Finding probabilityProbability is the ratio of required to the total possible outcomes of an event.
The required outcome = dark blue= 25Total possible outcomes= entire sample Space = 100P(dark blue ) = 40/100
divide through by 20
P(dark blue ) = 2/5
Therefore, the probability of landing on target is 2/5
Learn more on probability:https://brainly.com/question/24756209
#SPJ1
The product of two positive numbers is 56. If their difference is 10 , find the numbers.
Answers
According to loyalty card data, the amount of money spent per shopper at the grocery store is normally distributed with a mean of $75 per trip and a standard deviation of $25 per trip. How much money does a shopper spend that is at the 95th percentile of this distribution
Answers
Answer:
A shopper that is at the 95th percentile of this distribution spends $116.125.
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Mean of $75 per trip and a standard deviation of $25 per trip.
This means that \(\mu = 75, \sigma = 25\)
How much money does a shopper spend that is at the 95th percentile of this distribution?
This is X when Z has a p-value of 0.95, so X when Z = 1.645.
\(Z = \frac{X - \mu}{\sigma}\)
\(1.645 = \frac{X - 75}{25}\)
\(X - 75 = 1.645*25\)
\(X = 116.125\)
A shopper that is at the 95th percentile of this distribution spends $116.125.
PLEASE ANSWER UNDER 5 MIN!!!! ily!!!!
what is the period of the sinusoidal function? enter your answer in the box.

Answers
Answer:
Step-by-step explanation:
10
Ws
What is the estimated mean28-day strength of this concrete if the 7-day strength is 3000psi?
Answers
Answer:
12,000psi
Step-by-step explanation:
Given the 7 days strength of a concrete to be 3000psi, to calculate the estimated mean28-day strength of this concrete the following equality equation is applied
7 days strength = 3000psi
28days strength = y
To get y, we will Cross multiply
7 × y = 28×3000
7y = 28×3000
7y = 84000
Divide both sides by 7
7y/7 = 84000/7
y = 12000
hence the estimated mean 28-day strength of this concrete is 12,000psi
speeeeeeeeeeeddddddddddddddddd (might give brainlest

Answers
Answer:
6
Step-by-step explanation:
6 times 6 is 36 and the formula for area is
lxw(Length times width)
Someone please help me with this qiesrion pls

Answers
The true statement on the height of the ball when thrown from a building, given the equation, can be found to be A. The ball reaches the ground in 3 seconds.
How to find the height ?The equation given of the ball being thrown from a building, gives us the height when solved.
The height of the ball when it reaches the ground is 0 feet so we can insert this in the formula to find the time:
0 = - 5 ( t - 3 ) ( t + 5 )
We can use the zero product property, which states that if the product of two factors is zero, then at least one of the factors must be zero. So, we can set each factor equal to zero and solve for t:
t - 3 = 0 or t + 5 = 0
Solving for t in the first equation, we get:
t - 3 = 0
t = 3
Seeing as t is 3 seconds the first option is correct.
Find out more on height at https://brainly.com/question/12446886
#SPJ1
Find the power of 9↑1. Type your answer using digits.
Answers
Answer:
9^1 has a power of 1. it evaluates to 9
Step-by-step explanation:
Answer Explanation:
I have 3 red balls, 3 blue balls and 3 yellow balls in a box. Total of 9 balls. Let's say that I randomly pick 3 balls, what are the chances of having at least 2 red balls in the 3 that I picked?
Answers
The probability of having at least 2 red balls in the 3 that I picked will be 1/3.
What is probability?Its fundamental concept is that someone will nearly surely occur. The proportion of positive events in comparison to the total of occurrences.
Then the probability is given as,
P = (Favorable event) / (Total event)
I have 3 red balls, 3 blue balls, and 3 yellow balls in a crate. All out of 9 balls.
If the three balls are picked randomly, then the probability of having at least 2 red balls in the 3 that I picked will be given as,
P = 3/9
P = 1/3
The probability of having at least 2 red balls in the 3 that I picked will be 1/3.
More about the probability link is given below.
https://brainly.com/question/795909
#SPJ1
Anyone know how to get the answer for central angle , 1/2 central angle , apothem, and area

Answers
The measure of a central angle of a decagon is 36 degrees.
the 1/2 central angle = 18 degrees
Apothem ≈ 16.93
Area of the decagon ≈ 931.15
How to find the central angleThe figure has ten sides hence a decagon
To find the measure of a central angle of a decagon, we need to use the formula:
Central angle = 360 degrees / number of sides
Substituting the value for a decagon, we get:
Central angle = 360 degrees / 10 sides
Central angle = 36 degrees
To find the 1/2 central angle, we simply divide the central angle by 2:
1/2 central angle = 36 degrees / 2
1/2 central angle = 18 degrees
To find the apothem, we use the formula:
Apothem = (Side length) / (2 x tan(180 / number of sides))
Substituting the given values, we get:
Apothem = (11) / (2 x tan(18 degrees))
Apothem ≈ 16.93
To find the area of the decagon, we first need to find the perimeter using the formula:
Perimeter = (Number of sides) x (Side length)
Perimeter = 10 x 11
Perimeter = 110
Now, we can use the formula for the area:
Area = (1/2) x Apothem x Perimeter
Area = (1/2) x 16.93 x 110
Area ≈ 931.15
Learn more about decagon at:
https://brainly.com/question/29456443
#SPJ1
Anyone know how to do this?
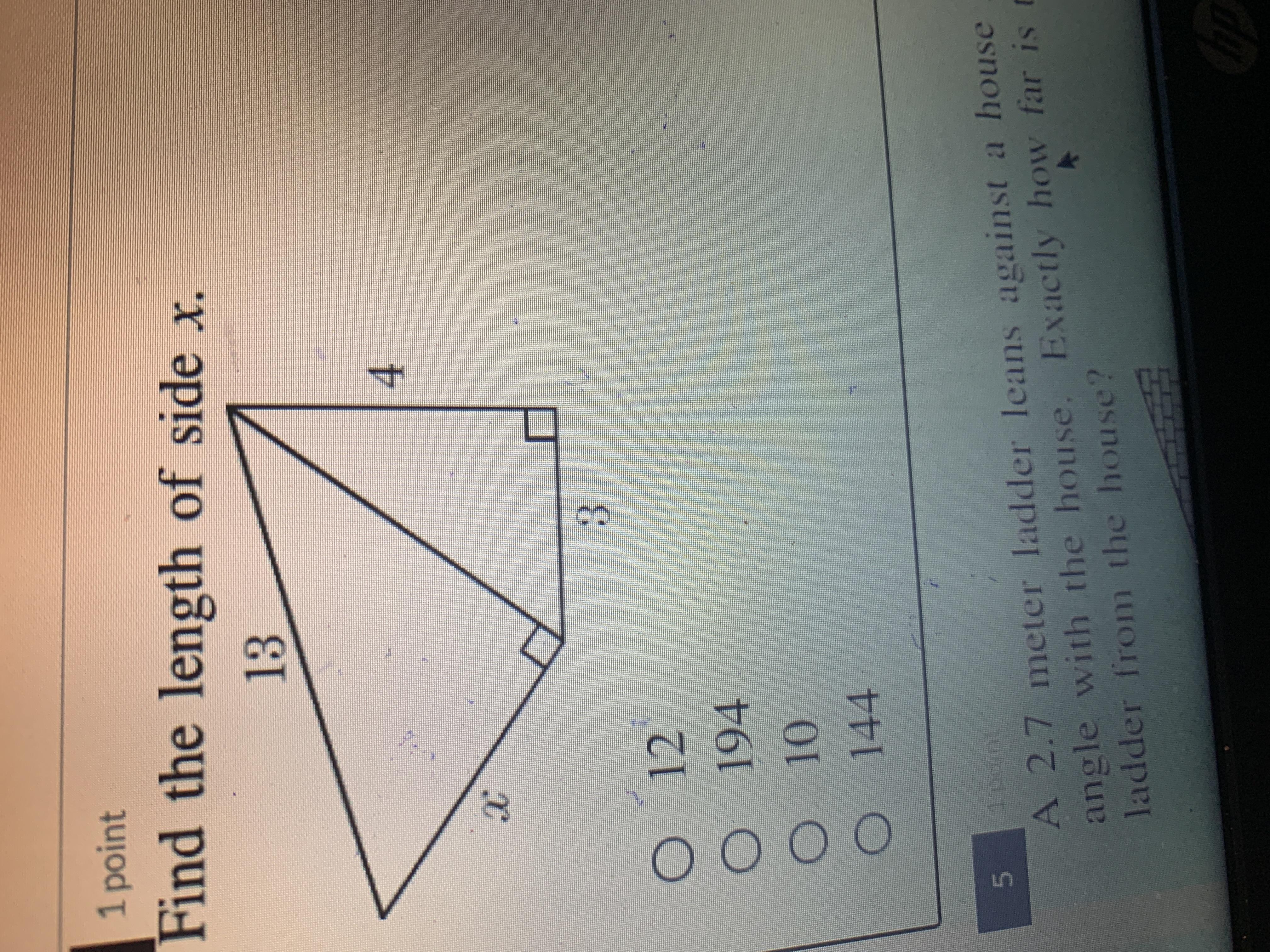
Answers
Answer:
It would be 10
Step-by-step explanation:
Its 10 because 12 is to long and the fact that 10 is a few inches shorter it looks correct :D
Answer:
A) 12
Step-by-step explanation:
Yes you have to do a² + b² = c²
So the bottom triangle is 3 and 4 so plug in.
4² + 3² = c² (simplify)
16 + 9 = c²
25 = c² (square root both sides)
5 = c
That gives us the vertical side of the second triangle.
So plug in again
5² + b² = 13² (simplify)
25 + b² = 169 (subtract 25 on both sides)
b² = 144 (square root both sides)
b = 12
x = 12
Hope this helps ya!!
