Simplify the expression below. 8^2-13 + 2^4 A. 11 B. 19 C. 59 D. 67
Answers
64 - 13 + 16
64 - 13 = 51
51 + 16 = 67
The answer choice is D.
Answer:
67Solution:
Simplify the exponents and add/subtract
=> \(8^2-13 + 2^4\)=> \(64 - 13 + 16\)=> \(67\)Hence, the answer is Option D (67).
Related Questions
Please helppp will give 15 Brainly
Answers
Answer:
What is 15 Brainly?
Step-by-step explanation:
Which fraction and decimal forms match the long division problem?

Answers
Answer: C
Step-by-step explanation: C
2 divided into 9 parts is 2/9.
Let's' explain this visually
Take this pizza, (image below)
Let's say we have two pizzas for 8 friends (including ourselves), so naturally, we'll cut the pizza's each into 9 slices, 1 for each, now everyone gets 1/9 of a pizza, but there are two pizzas, so if we add 1/9+1/9, we'll get two ninths.
Now 2/9=0.2 repeating!
This is how I got my answer sorry for the vague explanation

In order for a satellite to move in a stable
circular orbit of radius 6761 km at a constant
speed, its centripetal acceleration must be
inversely proportional to the square of the
radius r of the orbit. What is the speed of the satellite?
Find the time required to complete one orbit.
Answer in units of h.
The universal gravitational constant is
6. 67259 × 10^−11 N · m2/kg2 and the mass of
the earth is 5. 98 × 10^24 kg. Answer in units of m/s
Answers
The required answers are the speed of the satellite is `7842.6 m/s` and the time required to complete one orbit is `1.52 hours`.
Given that a satellite moves in a stable circular orbit of radius r = 6761 km and at constant speed.
And its centripetal acceleration is inversely proportional to the square of the radius r of the orbit. We need to find the speed of the satellite and the time required to complete one orbit.
Speed of the satellite:
We know that centripetal acceleration is given by the formula
`a=V²/r`
Where,a = centripetal accelerationV = Speed of the satellite,r = Radius of the orbit
The acceleration due to gravity `g` at an altitude `h` above the surface of Earth is given by the formula `
g = GM/(R+h)²`,
where `M` is the mass of the Earth, `G` is the gravitational constant, and `R` is the radius of the Earth.
Here, `h = 6761 km` (Radius of the orbit) Since `h` is much smaller than the radius of the Earth, we can assume that `R+h ≈ R`, where `R = 6371 km` (Radius of the Earth)
Then, `g = GM/R²`
Substituting the values,
`g = 6.67259 × 10^-11 × 5.98 × 10^24 / (6371 × 10^3)²``g = 9.81 m/s²`
Therefore, centripetal acceleration `a = g` at an altitude `h` above the surface of Earth.
Substituting the values,
`a = 9.81 m/s²` and `r = 6761 km = 6761000 m`
We have `a = V²/r` ⇒ `V = √ar`
Substituting the values,`V = √(9.81 × 6761000)`
⇒ `V ≈ 7842.6 m/s`
Therefore, the speed of the satellite is `7842.6 m/s`.
Time taken to complete one orbit:We know that time period `T` of a satellite is given by the formula
`T = 2πr/V`
Substituting the values,`
T = 2 × π × 6761000 / 7842.6`
⇒ `T ≈ 5464.9 s`
Therefore, the time required to complete one orbit is `5464.9 seconds` or `1.52 hours` (approx).
To know more about acceleration please visit :
https://brainly.com/question/460763
#SPJ11
I will give 30 points if u help now

Answers
Answer:
3. x=16
4. x=51
Step-by-step explanation:
3. 3x-8=x+24
2x=32
x=16
4. 2/3(x+27)= 180-(3x-25)
2/3x+18=180-3x+25
11/3x=187
11x=561
x=51
Step-by-step explanation:
Excercise 3:
By Alternate Exterior angles,
(x + 24)° = (3x - 8)°.
=> 2x = 32, x = 16.
Excercise 4:
By C-angles,
2/3 * (x + 27)° + (3x - 25)° = 180°.
=> 2x/3 + 18 + 3x - 25 = 180
=> 11x/3 = 187
=> x = 187 * (3/11) = 51.
3. The number of visitors to a website in the first week is 50. The number of visitors each week is double the number of visitors the previous week. What is the total number of visitors to the website in the first 8 week
Answers
The total number of visitors to the website in the first 8 weeks is 12,750.
To determine the total number of visitors to the website in the first 8 weeks, we can analyze the pattern of doubling the number of visitors each week.
Week 1: 50 visitors
Week 2: 2 * Week 1 = 2 * 50 = 100 visitors
Week 3: 2 * Week 2 = 2 * 100 = 200 visitors
Week 4: 2 * Week 3 = 2 * 200 = 400 visitors
Week 5: 2 * Week 4 = 2 * 400 = 800 visitors
Week 6: 2 * Week 5 = 2 * 800 = 1600 visitors
Week 7: 2 * Week 6 = 2 * 1600 = 3200 visitors
Week 8: 2 * Week 7 = 2 * 3200 = 6400 visitors
By following the pattern, we can see that each week the number of visitors doubles from the previous week.
To find the total number of visitors in the first 8 weeks, we sum up the number of visitors from each week:
Total number of visitors = Week 1 + Week 2 + Week 3 + Week 4 + Week 5 + Week 6 + Week 7 + Week 8
Total number of visitors = 50 + 100 + 200 + 400 + 800 + 1600 + 3200 + 6400
Total number of visitors = 12750
Therefore, the total number of visitors to the website in the first 8 weeks is 12,750.
For more such questions on number visit:
https://brainly.com/question/26460978
#SPJ8
a balloon is being filled with helim at the rate of 4 ft^3/moinj. the rate, in suare feet per minute, at which the surace area is increasing when the volume is 32 pi.3 ft ^3 is
Answers
The rate at which the surface area of the balloon is increasing when the volume is 32π.3 ft^3 is dr/dt = (1/4π)(dV/dt)/r^2.
We can relate the volume and surface area of a balloon using the formula for the volume of a sphere, which is V = (4/3)πr^3, and the formula for the surface area of a sphere, which is A = 4πr^2, where V is the volume and r is the radius of the balloon.
Given that the volume is 32π.3 ft^3, we can substitute this value into the volume formula to find the radius of the balloon. Since V = (4/3)πr^3, we have 32π.3 = (4/3)πr^3. Simplifying, we find r^3 = (3/4)(32π.3)/π, which gives r = 2.
To find the rate at which the surface area is increasing, we can differentiate the surface area formula with respect to time, using the chain rule. Let A be the surface area and t be the time. We are given that the volume is increasing at a rate of 4 ft^3/min. Using the related rates formula, dV/dt = 4 ft^3/min, we can solve for dr/dt, which gives dr/dt = (1/4π)(dV/dt)/r^2.
Substituting the given volume V = 32π.3 ft^3 and the radius r = 2 into the expression for dr/dt, we can calculate the rate at which the surface area is increasing. By plugging in these values, we can find the rate at which the surface area is increasing when the volume is 32π.3 ft^3.
Learn more about volume here:
https://brainly.com/question/30347304
#SPJ11
10 divided by 3.95 times 67=3?
Answers
Answer: (Decimal: x = 0.99746…)
Step-by-step explanation:
Which problem can be solved using the equation 9x + 14 = 100
Answers
Answer:
rounded form: x = 9.56
Step-by-step explanation:
9x + 14 =100
you would 1st subtract 14 from 100 so you're left with
9x = 86
now to get x alone, you divide both sides by 9 so now you have
x = 9.56
If a = 4+3√5 and b = 1 then what will be the value of 2 + 2 ?

Answers
Answer:
is this a trick question? the value of 2+2 = 4
if you are asking what a^2 + b^2 is then ... 1/a^2 + 45a^2 + 61
Step-by-step explanation:
I just need to know if the answer is B or D

Answers
Step 1. The two functions we have are:
\(\begin{gathered} f(x)=2x^2 \\ g(x)=\sqrt[]{x-2} \end{gathered}\)And we are asked to find the composite function f(g(x)) and the domain.
Step 2. The function that we need to find is:
\(f(g(x))\)To find this, we substitute g(x) into the x value of f(x):
\(f(g(x))=2(\sqrt[]{x-2})^2-1\)Step 3. Simplifying:
The square root and the power of two cancel each other
\(f(g(x))=2(x-2)^{}-1\)Distributing the multiplication by 2:
\(f(g(x))=2x-4-1\)Combining the like terms:
\(f(g(x))=\boxed{2x-5}\)Step 4. Find the domain. The domain is the set of possible values that the x variable can take.
Remember the two original functions:
\(\begin{gathered} f(x)=2x^2 \\ g(x)=\sqrt[]{x-2} \end{gathered}\)for f(x) x can take any value. But for g(x) the square root cannot be a negative number, therefore, x-2 has to be equal to or greater than 0:
\(\begin{gathered} \text{Domain:} \\ x-2\ge0 \end{gathered}\)Solving for x:
\(\begin{gathered} \text{Domain:} \\ x\ge2 \end{gathered}\)This domain also applies to the composite function f(g(x)), and it can be written as follows:
\(D\colon\mleft\lbrace x|x\ge2\mright\rbrace\)Answer: Option four
\(\begin{gathered} f(g(x))=2x-5 \\ D\colon\lbrace x|x\ge2\rbrace \end{gathered}\)(a) Determine the smallest positive value of n for which a simple graph on n vertices and 2n edges can exist. Give an example of such a graph for the smallest n. (b) Let G be a simple graph with 20 vertices. Suppose that G has at most two com- ponents, and every pair of distinct vertices u and v satisfies the inequality that deg(u) + deg(v) > 19. Prove that G is connected.
Answers
(a) The smallest positive value of n for which a simple graph on n vertices and 2n edges can exist is 3. An example of such a graph for the smallest n is a triangle, where each vertex is connected to the other two vertices.
In this case, we have 3 vertices and 2n = 2 * 3 = 6 edges, which satisfies the condition.
To determine the smallest positive value of n, we need to consider the conditions for a simple graph:
1. Each vertex must be connected to at least one other vertex.
2. There should be no multiple edges between the same pair of vertices.
3. There should be no self-loops (edges connecting a vertex to itself).
Considering these conditions, we start by trying with the smallest possible n, which is 3. We construct a graph with 3 vertices and connect each vertex to the other two vertices, resulting in a triangle. This graph satisfies the conditions and has 2n = 2 * 3 = 6 edges.
(b) To prove that G is connected, we will use a proof by contradiction.
Assume that G is not connected, meaning it has two or more components. Let's consider two distinct components, C1 and C2.
Since G has at most two components, each component can have at most 10 vertices (20 vertices / 2 components). Let's assume C1 has x vertices and C2 has y vertices, where x + y ≤ 20.
Now, let's consider two vertices u and v, where u belongs to C1 and v belongs to C2. According to the given condition, deg(u) + deg(v) > 19.
Since deg(u) represents the degree of vertex u, it means the number of edges incident to vertex u. Similarly, deg(v) represents the degree of vertex v.
In C1, the maximum possible degree for a vertex is x - 1 (since there are x vertices, each connected to at most x - 1 other vertices in C1). Similarly, in C2, the maximum possible degree for a vertex is y - 1.
Therefore, deg(u) + deg(v) ≤ (x - 1) + (y - 1) = x + y - 2.
But according to the given condition, deg(u) + deg(v) > 19. This contradicts the assumption that G has at most two components.
Hence, our assumption that G is not connected is false. Therefore, G must be connected.
In conclusion, if a simple graph G has 20 vertices, at most two components, and every pair of distinct vertices satisfies the inequality deg(u) + deg(v) > 19, then G is connected.
To learn more about vertices, click here: brainly.com/question/31767946
#SPJ11
Please help mee !!!!!!!

Answers
Answer:
Quadrilateral
Step-by-step explanation:
Its a quadrilateral. Quadrilateral means four sided shape, and the pic above shows a four sided shape
Which statement is true?

Answers
question choices
85
50
42.5
59
1.7
PLEASE HELP PLS

Answers
Answer:
42.5
Step-by-step explanation:
Multiply 50 by 0.85, which equals 42.5.
The ratio of fiction books to non-fiction books in Roxanne's library is 7 to 4 if roxxanne owns 182 fiction books, how man non-fiction books does she own
Answers
Answer:
Step-by-step explanation:
let she have x non fiction books
ratio of fiction books to non fiction books is 7:4
7/4=182/x(do cross multiplication)
4*182=7*x
728/7=x
104=x
therefore she has 104 non fiction books
The number of non-fiction books read by Roxanne is 104.
What is the application ratio and proportion?
A ratio is the relation between two numbers as a / b. A proportion is the equality of two ratios as a / b = c / d.
Ratio and proportion can be applied to solve Mathematical problems dealing with unit values of the quantities.
Given that,
The ratio of fiction books to non-fiction books is 7 : 4.
The number of fiction books is 182.
Suppose the number of non-fiction books be x.
Then, 7 : 4 = 182 : x
=> 7/4 = 182/x
=> x = (182 × 4)/7
= 104
Hence, the number of non-fiction books read is 104.
To know more about ratio and proportion click on,
brainly.com/question/14279414
#SPJ2
a 1 =−4a, start subscript, 1, end subscript, equals, minus, 4 a_i = a_{i - 1} \cdot 2a i =a i−1 ⋅2
Answers
The given equation is a recursive formula where a subscript i equals the product of a subscript i-1 and 2, with the initial value of a subscript 1 being -4a.
The equation represents a recursive relationship between the terms of the sequence. Starting with the initial term, a subscript 1, the subsequent terms are determined by multiplying the previous term, a subscript i-1, by 2. This recursive formula can be written as a subscript i = a subscript i-1 * 2.
Given that a subscript 1 = -4a, we can use this initial value to find the subsequent terms of the sequence. To calculate a subscript 2, we substitute i = 2 into the formula:
a subscript 2 = a subscript 2-1 * 2 = a subscript 1 * 2 = -4a * 2 = -8a.
Similarly, for a subscript 3:
a subscript 3 = a subscript 3-1 * 2 = a subscript 2 * 2 = -8a * 2 = -16a.
By applying the recursive formula repeatedly, we can generate the terms of the sequence. Each term is obtained by multiplying the previous term by 2.
Learn more about recursive formula here:
https://brainly.com/question/1470853
#SPJ11
A cylinder has a base radius of 5 inches and a height of 6 inches. What is its volume in cubic inches, to the nearest tenths place?
Answers
Answer:
V≈471.24
or to the nearest tenth is
471.2
Answer:
471.2
Step-by-step explanation:
Find the union, AUB, for of the following pair of sets. Enter "DNE" for the empty set.A = (-∞, - 5], B = [5, ∞)
![Find the union, AUB, for of the following pair of sets. Enter "DNE" for the empty set.A = (-, - 5], B](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/CzGGjQ94qMYNA1yvK5G49HCYGWV3sHjA.jpeg)
Answers
Given
Two sets A = (-∞, - 5], B = [5, ∞)
Find
union, AUB
Explanation
Union of two sets A and B is the set of all elements that are present in A or in B
so , here A = (-∞, - 5], B = [5, ∞)
then union of set A and B is given by
\(A\cup B=(-\infty,-5]\cup[5,\infty)\)Final Answer
Therefore., the union of A and B is (-∞, - 5] U [5, ∞)
Challenge #5: Shade all the points but leave the targets exposed with the fewest inequalities
Answers
The inequalities equation which will shade all the points except target point are, y >= 2, y >= -3.5x + 4.5 and y <= 1.25x - 1.5.
The line passing through P(-1,2) and P(-4,2) has a slope of 0 and a y-intercept of 2, so its equation is y = 2. The line passing through P(-1,2) and P(-2,0.5) has a slope of -3.5 and a y-intercept of 4.5, so its equation is y = -3.5x + 4.5. The line passing through P(-2,0.5) and P(-4,2) has a slope of 1.25 and a y-intercept of -1.5, so its equation is y = 1.25x - 1.5.
Now we can create a system of inequalities that will shade all of the points except for T(-2,2). We can do this by making sure that the inequality for each line is greater than or equal to the target point on one side of the line, and less than or equal to the target point on the other side of the line.
For the line y = 2, we can write the inequality y >= 2 on the side of the line that contains the target point T(-2,2). For the line y = -3.5x + 4.5, we can write the inequality y >= -3.5x + 4.5 on the side of the line that contains the point T(-2,2). For the line y = 1.25x - 1.5, we can write the inequality y <= 1.25x - 1.5 on the side of the line that contains the point T(-2,2).
Putting all of these inequalities together, we get:
y >= 2 (for the line passing through P(-1,2) and P(-4,2))
y >= -3.5x + 4.5 (for the line passing through P(-1,2) and P(-2,0.5))
y <= 1.25x - 1.5 (for the line passing through P(-2,0.5) and P(-4,2))
These inequalities should shade all of the points except for the target point T(-2,2), and they should do so with the fewest number of inequalities possible.
To know more about inequalities, here
brainly.com/question/30219862
#SPJ4
--The complete question is, With the fewest inequalities, shade all the points but leave the targets exposed. Write the inequality equations to do this.
Points are P(-1,2), P(-4,2) and P(-2, 0.5)
T(-2,2)
Graph is show in the image.--

of 4
Workers in an office of 40 staff were asked their favourite type of take-away.
The results are summarised in the table.
Take-away
Pizza
Curry
Fish & chips
Kebab
Other
What fraction of a person is one degree?
Give your answer in its simplest form.
Frequency
4
4
8
5
19
Angle
a
b
C
d
e

Answers
Workers in an office of 40 staff were asked their favourite type of take- away.1/9 bit of a person is one degree.
What's Fraction?
An element of a total is a bit. The number is represented mathematically as a quotient, where the numerator and denominator are resolve. Both are integers in a simple bit. A bit appears in the numerator or denominator of a complex bit. The numerator of a proper bit is lower than the denominator.
The magnitude of an angle is measured using a unit of dimension. In magnitude, 1 degree is original to1/360 of a full gyration.
Degree 1 – direct.
Degree 2 – quadratic.
Degree 3 – boxy.
Degree 4 – quartic( or, if all terms have indeed degree, biquadratic)
Given that;
total workers = 40
Bit of a person = 1 degree
we know that 360 ° = 40 person
so for 1 degree = 40/360 = 1/9
Hence,1/9 bit of a person is one degree.
Learn more about Fraction click here:
https://brainly.com/question/86977
#SPJ1
Solve the equation for x
z=m+x-y a)x=-z+m+y b)x=z-m+y c)x=z+m-y d)x=z+y+m
Answers
Answer:
x = z - m + y
Step-by-step explanation:
Given:
\(\displaystyle \large{z = m+x-y}\)
To solve for x-term, we have to isolate it. We can do by subtracting m-term both sides and add y-term both sides.
\(\displaystyle \large{z-m+y=m+x-y-m+y}\\\\\displaystyle \large{z-m+y=x}\\\\\displaystyle \large{x=z-m+y}\)
Therefore, the answer to this question is x = z - m + y
Please let me know if you have any questions regarding my answer or explanation!
HELPPPPPP ITS FOR MY FINALLLL
click the photo below

Answers
Answer:
28
Step-by-step explanation:
▪︎ ADE and ABC are similar triangles (AAA)
▪︎ DA = DB + BA = 30 + 12 = 42
▪︎ k = DA / BA = 42 / 12 = 3.5
▪︎ DE = BC * k = 8 * 3.5 = 28
A plane intersects only one nappe of a double-napped cone such that it is parallel to a generating line. Which conic section is formed?.
Answers
When a plane intersects only one nappe of a double-napped cone such that it is parallel to a generating line, it forms a parabola.
When a plane intersects only one nappe of a double-napped cone parallel to a generating line, it forms a conic section known as a parabola. This is because a parabola is defined as the set of all points that are equidistant to a fixed point (known as the focus) and a fixed line (known as the directrix).
When a plane intersects a double-napped cone parallel to a generating line, it intersects all the generatrices at the same angle, resulting in a curve that is symmetric and opens in one direction. This curve is a parabola, and it is commonly found in nature, such as the path of a thrown ball, the shape of a satellite dish, or the reflector of a car's headlights.
The properties of a parabola make it useful in various fields, including optics, physics, and engineering, where it is used to model and analyze a wide range of phenomena, such as the trajectory of projectiles, the behavior of lenses and mirrors, and the design of antennas and reflectors.
To know more about parabola:
https://brainly.com/question/21685473
#SPJ4
mthwetew can build a block wall in 3 days. andy can build the wall in 5 days. how long will it take if they work together?
Answers
It will take Mthwetew and Andy 1.875 days to build the block wall if they work together.
Hello! I understand that you'd like to know how long it will take Mthwetew and Andy to build a block wall if they work together. To answer this question, we will use the concept of work rates.
Mthwetew can build a wall in 3 days. This means Mthwetew's work rate is 1/3 (wall/day).
Andy can build the same wall in 5 days. This means Andy's work rate is 1/5 (wall/day).
To find out how long it will take them to build the wall together, we will add their work rates and solve for the time it would take them to complete the task.
Combined work rate: (1/3) + (1/5)
To add these fractions, find a common denominator, which in this case is 15.
(1/3) * (5/5) = 5/15
(1/5) * (3/3) = 3/15
Now, add the numerators:
5/15 + 3/15 = 8/15 (wall/day)
Their combined work rate is 8/15 (wall/day). To find out how long it takes them to build the wall together, we need to calculate the reciprocal of their combined work rate:
15/8 = 1.875 days
So, it will take Mthwetew and Andy 1.875 days to build the block wall if they work together.
for more questions on days
https://brainly.com/question/24900258
#SPJ11
if 5y - 8 < 12, what is the maximum possible value of 10y ?
Answers
Answer: The maximum possible value of y is 30 ;)
reflect..............................................

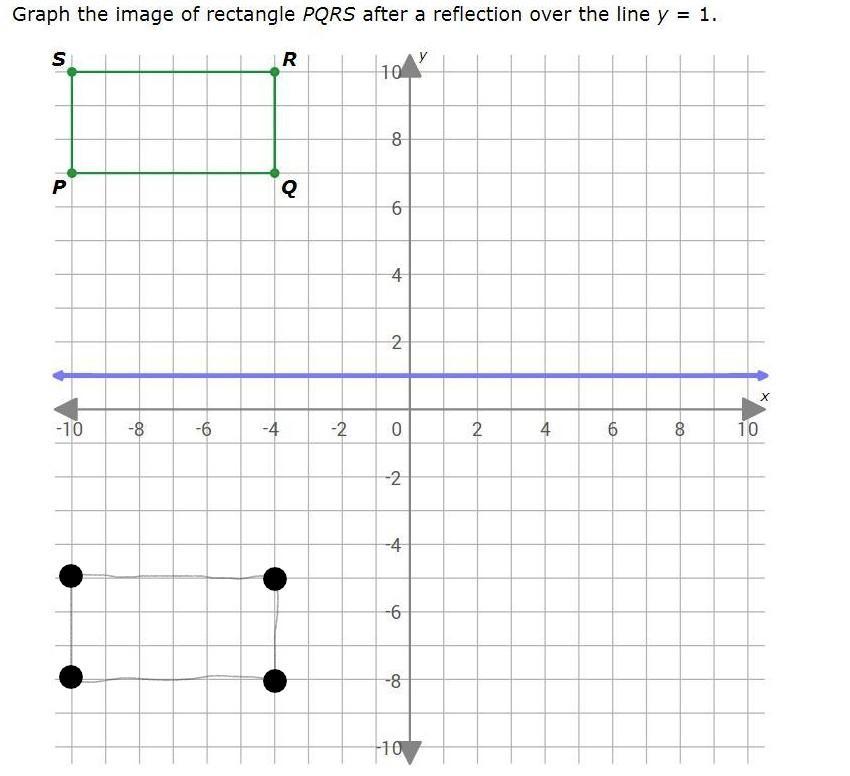
Answers
Answer:
Q (-4,-5)
R (-4,-8)
P (-10,-5)
S (-10,-8)
Step-by-step explanation:
The estimated population of a certain city over time is given in the table below. Answer the questions below to determine what kind of function would best fit the data, linear or exponential. 27909 23672
Number of Years Since Last Census, x
1
2
3
4
Estimated Population, f(x)
27909
23672
19401
15151
Box 1: Linear or Exponential?
Box 2: Additively or Multiplicatively?
Box3: Common difference or common ratio
Box4: Answer to box 3

Answers
Answer:
A linear function would better model the data because as x increases, the y values change additively, The common difference of the function is approximately 4253
Step-by-step explanation:
A linear function would better model the data because as x increases, the y values change additively,
(e.g, x from 1 to 2, so, y from 27909 to 23672
The difference is 27909 - 23672 = 4237
from 2 to 3, 23672 to 19401 with difference 23672 - 19401 = 4271
from 3 to 4, 19401 to 15151 with difference 19401 - 15151 = 4250)
The common difference of this is approximately, we use average of all the differences we have found above, so,
Average difference = (4237 + 4271 + 4250)/3 = 4253
The approximate common difference is 4253
A rectangular container 6.5 ft long, 3.2 ft wide and 2 ft high is filled with sand to a depth of 1.3 ft. How much sand is in the container?
Answers
Answer:
Therefore, there are 27.04 cubic feet of sand in the container.
Step-by-step explanation:
We can start by calculating the volume of the rectangular container:
Volume = length x width x height
Volume = 6.5 ft x 3.2 ft x 2 ft
Volume = 41.6 cubic feet
Since the sand fills the container to a depth of 1.3 feet, we can calculate the volume of the sand as follows:
Volume of sand = length x width x depth of sand
Volume of sand = 6.5 ft x 3.2 ft x 1.3 ft
Volume of sand = 27.04 cubic feet
Therefore, there are 27.04 cubic feet of sand in the container.
For any function, we call x the ____________ value and y is the _______________ value.
Answers
A fireman’s ladder leaning against a house makes an angle of 62 with the ground. If the ladder is 3 feet from the base of the house, how long is the ladder?
Answers
In the given scenario ladder is 6.52 feet long.
Given that,
The angle between ground and ladder = 62 degree
The distance of ladder from ground and ladder = 3 feet
We have to find the length of ladder.
Since we know that,
The trigonometric ratio
cosθ = adjacent/ Hypotenuse
Here we have,
Adjacent = 3 feet
Hypotenuse = length of ladder
Thus to find the length of ladder we have to find the value of hypotenuse.
Therefore,
⇒ cos62 = 3/ Hypotenuse
⇒ 0.46 = 3/ Hypotenuse
⇒ Hypotenuse = 3/0.46
= 6.52
Thus,
length of ladder = 6.52 feet.
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ1
