six more than twice a number is ten. find the number 8th grade math
write the equation
solve for the variable
Answers
Answer:
x = 2
Step-by-step explanation:
Equation: 2x + 6 = 10
2x = 4
x = 2
Answer:
let the number be x
then
2x + 6 = 10
2x = 10-6
2x = 4
x = 2
mark me as brainliest
Related Questions
find the lateral surface area of the prism
Answers
The lateral surface area of a prism is the sum of the areas of all its rectangular faces.
What is surface area?Surface area is a two-dimensional measure that refers to the total area of a surface, such as the area of a two-dimensional shape, a three-dimensional solid, or a combination of both. It is the sum of the areas of all the faces of a solid object. It is also referred to as the area of the boundary of a three-dimensional object. It can be used to calculate the volume of an object, and is also used in other calculations like area of the base of a triangle, area of a circle, and more.
It is calculated by multiplying the perimeter of the base by the height of the prism. For example, if the base of a prism is a square with side length s and the height is h, then the lateral surface area of the prism can be calculated as 4sh. If the base of the prism is a rectangle with length l and width w, then the lateral surface area of the prism can be calculated as 2lw + 2wh.
The lateral surface area of a prism can also be calculated by adding the areas of the triangular faces. If the base of the prism is a triangle with side lengths a, b, and c, then the lateral surface area of the prism can be calculated as a + b + c.
It is important to note that the lateral surface area of a prism is different from its surface area. The surface area of a prism is the sum of the areas of its lateral faces and its two bases.
To know more about surface area click-
brainly.com/question/1297098
#SPJ1
Complete question:
How to find the lateral surface area of the prism?
A researcher collected data on the latitude, in degrees north of the equator, and the average low temperature, in degrees Fahrenheit, for a random sample of cities in Europe. The data were used to create the following equation for the least-squares regression line. predicted average low temperature=65.5−0.70(latitude) Which of the following is the best interpretation of the slope of the line?
Answers
The best interpretation of the slope of the linear regression equation is given as follows:
For each increase of one degree of latitude, the average low temperature decreases by 0.70 degrees Fahrenheit.
What is the slope of a linear function?The slope represents the rate of change of the output variable relative to the input variable of a linear relation.
Hence, it can be said that the slope states by how much the output variable y changes when the input variable x is increased by 1.
The variables in this problem are given as follows:
Input: Latitude.Output: average low temperature.The negative slope of -0.7 means that for each increase of one degree of latitude, the average low temperature decreases by 0.70 degrees Fahrenheit.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
Answer:
B
Step-by-step explanation:
Simplify the expression: 3(x + 3)
Answers
Answer:
3x + 9
Step-by-step explanation:
Makesha lost 58.5 pounds in 18 weeks. Find her rate of loss in pounds per week.
Answers
Suppose that you are taking a course that has 4 tests. The first three tests are each worth 20% of your final grade, and the fourth test is worth 40% of the final grade. To get a B in the course, you must have an average of at least 80 percent on the 4 tests. Your scores on the first 3 tests were 63.5 %, 76 %, and 87 %. What is the minimum score you need on the fourth test to get a B for the course?. Don't round your answer.
Answers
Answer:
86.75
Step-by-step explanation:
Given test scores of 63.5, 76, and 87 that each count for 20% of your grade, you want to know the fourth test score needed for an average of 80, if the fourth test is worth 40% of your grade.
Course gradeThe grade for the course, with fourth test score x, will be ...
0.20(63.5 +76 +87) +0.40x = 80
0.40x +45.3 = 80
Solving for x, we get ...
0.40x = 34.7 . . . . subtract 45.3
x = 86.75 . . . . . . . divide by 0.4
The minimum score you need on the fourth test is 86.75.
<95141404393>

Find a and b using the factor theorem.
\(f(x)=x^3+ax^2+bx-12\) has factor \((x-1), (x+1)\)
Answers
The values of a and b using the factor theorem for the polynomial f(x), we set f(1) and f(-1) equal to zero. Solving the resulting system of equations, we find that a = 12 and b = -1.
To find the values of a and b using the factor theorem, we need to use the given factors (x - 1) and (x + 1) and the fact that they are roots of the polynomial f(x).
The factor theorem states that if (x - c) is a factor of a polynomial, then f(c) = 0. Therefore, we can set x = 1 and x = -1 in the polynomial f(x) to get two equations.
First, let's substitute x = 1 into f(x):
f(1) = (1)^3 + a(1)^2 + b(1) - 12
f(1) = 1 + a + b - 12
Next, let's substitute x = -1 into f(x):
f(-1) = (-1)^3 + a(-1)^2 + b(-1) - 12
f(-1) = -1 + a - b - 12
Since (x - 1) and (x + 1) are factors, f(1) and f(-1) must equal zero. Therefore, we can set the two equations equal to zero and solve for a and b:
1 + a + b - 12 = 0
-1 + a - b - 12 = 0
Rearraning the equations, we have:
a + b = 11
a - b = 13
Now, we can solve this system of equations. Adding the two equations, we get:
2a = 24
a = 12
Substituting the value of a into one of the equations, we find:
12 - b = 13
b = -1
Therefore, the values of a and b are 12 and -1 respectively.
For more such questions on polynomial
https://brainly.com/question/1496352
#SPJ8
express 7π/6 in degrees
Answers
Answer:
210°
Step-by-step explanation:
To change from radians to degrees, multiply 7π/6 by 180/π
That will give 210°
Would appreciate a Brainliest if this helped :)
Pls help me last question on math I got to finish the packet

Answers
The solutions to the linear function are;
1. The soccer team makes more money per car ($8) than the French club ($5).
2. The graph that demonstrates Arnold's journey is graph 3
3. The graph that demonstrates Francisco's journey is graph 1
4. The graph that demonstrates Celia's journey is graph 2
How do you solve for the linear function?
To determine which group makes the most money per car, we can calculate the slope of the linear function representing the amount earned per car washed for both the French club and the soccer team. The slope of a linear function is the change in the dependent variable (y) divided by the change in the independent variable (x).
Let's calculate the slope for the soccer team. We can choose any two points to calculate the slope. Let's use the points (3, 24) and (6, 48):
Slope (m) = (change in y) / (change in x) = (48 - 24) / (6 - 3) = 24 / 3 = 8
The soccer team earns $8 per car washed.
We can choose any two points to calculate the slope for the French club. Let's use the points (2, 10) and (4, 20):
(20 - 10) / (4 - 2) = 10 / 2 = 5
The French club earns $5 per car washed
The above answer is dependent on the questions below;
The french club and soccer team are washing cars to earn money. The amount earned, (y) dollars for washind (x) cars is a linear function. Which group makes the most money per car? explain
French club
Number of cars (x) Amount earned (y)
2 10
4 20
6 30
8 40
10 50
Soccer team
Number of cars (x) Amount earned (y)
3 24
6 48
9 72
Find more exercises on linear function;
https://brainly.com/question/20286983
#SPJ1
(6-2x) +(15-3x) where x=0.2
Answers
\( \sf{\blue{«} \: \pink{ \large{ \underline{A\orange{N} \red{S} \green{W} \purple{E} \pink{{R}}}}}}\)
Expression: \(\displaystyle\sf (6-2x) +(15-3x)\)
Substituting \(\displaystyle\sf x=0.2\):
\(\displaystyle\sf (6-2(0.2)) +(15-3(0.2))\)
Simplifying the expression inside the parentheses:
\(\displaystyle\sf (6-0.4) +(15-0.6)\)
\(\displaystyle\sf 5.6 +14.4\)
Calculating the sum:
\(\displaystyle\sf 20\)
Therefore, \(\displaystyle\sf (6-2x) +(15-3x)\) evaluated at \(\displaystyle\sf x=0.2\) is equal to \(\displaystyle\sf 20\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Homework part2 need help asap

Answers
The key features of the given quadratic functions are listed below.
What is the graph of a quadratic function?In Mathematics and Geometry, the graph of any quadratic function would always form a parabolic curve because it is a u-shaped. Based on the first quadratic function, we can logically deduce that the graph is an upward parabola because the coefficient of x² is positive and the value of "a" is greater than zero (0) i.e 3 > 0.
For the quadratic function y = 3x² - 5, the key features are as follows;
Axis of symmetry: x = 0.
Vertex: (0, -5).
Domain: [-∞, ∞]
Range: [-5, ∞]
For the quadratic function y = -2x² + 12x - 15, the key features are as follows;
Axis of symmetry: x = 3.
Vertex: (3, 3).
Domain: [-∞, ∞]
Range: [-∞, 3]
For the quadratic function y = -x² + 1, the key features are as follows;
Axis of symmetry: x = 0.
Vertex: (0, 1).
Domain: [-∞, ∞]
Range: [-∞, 1]
For the quadratic function y = 2x² - 16x + 30, the key features are as follows;
Axis of symmetry: x = 4.
Vertex: (4, -2).
Domain: [-∞, ∞]
Range: [-2, ∞]
Read more on quadratic functions here: brainly.com/question/24020644
#SPJ1

Evaluate the expression
6n + 3 if n=4
Answers
Answer:
27
Step-by-step explanation:
If n = 4, all we need to do is substitute the number into the equation.
6n + 3
= 6(4) + 3
= 24 + 3
= 27
I recommend checking out a few more problems like these to get the gist of it. You'll be using this a lot in the future! I recommend taking a look on Kahn Academy for more learning.
Good luck!
Type the correct answer in the box. Figure 1 is similar to figure 2. The height of the cone in figure 2 is centimeters.
On Plato!!!
Answers
The height of the cone in figure 2 is 4.5 centimeters.
Similar figureTwo figures are said to be similar if they have the same shape and the ratio of their corresponding sides are in the same proportion.
From the diagram, the two cone are similar. Let h represent the height of the cone in figure 2, hence:
h/3 = 12/8
h = 4.5 cm
The height of the cone in figure 2 is 4.5 centimeters.
Find out more on Similar figure at: https://brainly.com/question/4014697
Answer:
4.5
Step-by-step explanation:
Find slope of (- 6,1)and(8,-7)
Answers
The slope of the line passing through the points (-6, 1) and (8, -7) is -4/7.
What is the slope of the given points?Slope is simply expressed as change in y over the change in x.
Slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Given the data in the question;
Point A: ( -6,1 )
x₁ = -6
y₁ = 1
Point B: ( 8,-7 )
x₂ = 8
y₂ = -7
Now, plug the given x and y values into the slope formula above and simplify:
\(Slope\ m = \frac{y_2 - y_1}{x_2 - x_1} \\\\Slope\ m = \frac{-7 - 1}{8 - (-6)} \\\\Slope\ m = \frac{-7 - 1}{8 + 6} \\\\Slope\ m = \frac{-8}{14} \\\\Slope\ m = -\frac{4}{7}\)
Therefore, the slope of the line is -4/7.
Learn more about slope formula here: brainly.com/question/24578307
#SPJ1
he roots of the function f(x) = x2 – 2x – 3 are shown. What is the missing number?
x = –1 and x =
Answers
When is 9+10 really equal to 21
Answers
Answer:
it's equal to 21 when I say it's equal to 21
Use the scenario below to determine the correct values of n, p, q and x of the binomial distribution.
Suppose that in a certain video game there is a 1.9% item drop rate of frozen rain after defeating a Frigid Element.
What is the probability that 2 frozen rains will drop if 20 Frigid Elements are defeated?
n=
p=
q=
X =
Answers
The probability of obtaining exactly 2 frozen rains after defeating 20 Frigid Elements in the video game is approximately 0.2713 or 27.13%.
q = 1 - p
q = 1 - 0.019
q = 0.981
X: The number of successful outcomes.
In this scenario, we can model the situation using a binomial distribution. Let's determine the values of n, p, q, and X:
n: The number of trials or attempts.
In this case, the number of trials is the number of Frigid Elements defeated, which is given as 20.
n = 20
p: The probability of success on a single trial.
The probability of a frozen rain item dropping after defeating a Frigid Element is given as 1.9%, which can be expressed as 0.019.
p = 0.019
q: The probability of failure on a single trial.
The probability of failure is the complement of the probability of success. Therefore:
q = 1 - p
q = 1 - 0.019
q = 0.981
X: The number of successful outcomes.
We want to find the probability of 2 frozen rains dropping, so X is 2.
X = 2
Now that we have determined the values, we can calculate the probability using the binomial distribution formula. The formula for the probability mass function of the binomial distribution is:
P(X = x) = \((nCx) * (p^x) * (q^(n-x))\)
where nCx represents the binomial coefficient, which is the number of ways to choose x successes out of n trials.
Using this formula, we can substitute the values into the equation:
P(X = 2) = \((20C2) * (0.019^2) * (0.981^(20-2))\)
Calculating the binomial coefficient:
(20C2) = (20!)/(2!(20-2)!)
= (20 * 19 * 18!)/(2 * 18!)
= (20 * 19)/(2 * 1)
= 190
Now substituting the values:
P(X = 2) = \(190 * (0.019^2) * (0.981^18)\)
Now we can calculate the probability:
P(X = 2) ≈ 0.2713 or 27.13% (rounded to two decimal places)
Therefore, the probability of obtaining exactly 2 frozen rains after defeating 20 Frigid Elements in the video game is approximately 0.2713 or 27.13%.
For such more questions on Prob of 2 FRains
https://brainly.com/question/29127119
#SPJ8
A model train is built at a scale of 1 to 60. If the model train is 10 inches long, how many feet long is the actual train?

Answers
Answer:
60 feet
Step-by-step explanation:
please help me im doing pre alg and i cant figure out wether i shade up or to the side; graph x > 1
Answers
The representations of the inequality is an open circle is at 1 and a bold line starts at 1 and is pointing to the right.
How to graph an inequality?An inequality compares two values, showing if one is less than, greater than, or simply not equal to another value e.g. 5 < 6, x ≥ 2, etc.
Since our answer is x > 1. An open circle will be at 1 and a bold line starts at 1 and is pointing to the right (>). Check the attached image.
Note: You only shade up if you have ≤ (less than or equal) or ≥ (greater than or equal).
Learn more about inequality on:
brainly.com/question/25275758
#SPJ1

Solve for the missing side in the right triangle.
A) 5
B) 12
C) 13
D) 17
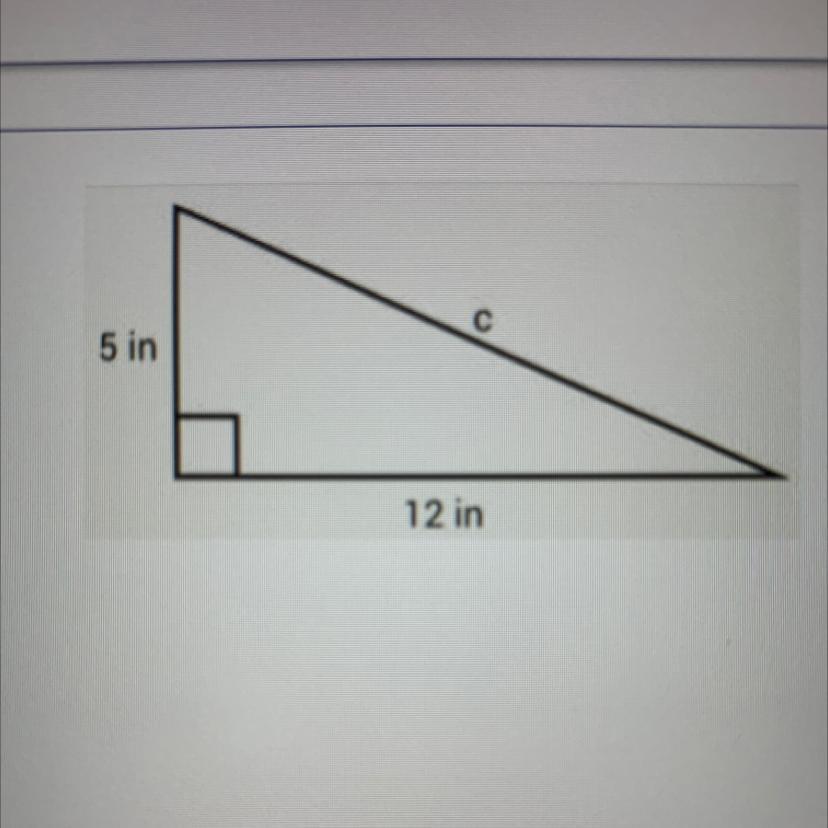
Answers
Answer:
c) 13
Step-by-step explanation:
\( {a}^{2} + {b}^{2} = {c}^{2} \\ {5}^{2} + {12}^{2} = {c}^{2} \\ 25 + 144 = {c}^{2} \\ 169 = {c}^{2} \\ c = 13\)
Answer:
C) 13
Step-by-step explanation:
Using the formula: \(a^{2} +b^{2}=c^{2}\), we can plug in 5 into a and 12 into b, since c is always the hypotenuse. Plug those numbers into the formula: \(5^{2} + 12^{2} =c^{2}\) and you get 25 + 144 = \(c^{2}\) or 169 = \(c^{2}\). You can then get rid of the square on the c by finding the square root of both sides. So, the square root of 169 would give you the answer of 13.
A cone has an apex. True False
Answers
Answer:
True, a cone has an apex which is the point where the sides of the cone meet to form a tip.
Suppose that f and g are functions that are differentiable at x = 1 and that f(1) = 2, f '(1) = −1, g(1) = −2, and g'(1) = 3. Find h'(1). h(x) = (x2 + 8)g(x)
Answers
Answer:
\(h'(1) = 23\)
Step-by-step explanation:
Let be \(h(x) = (x^{2}+8)\cdot g(x)\), where \(r(x) = x^{2} + 8\). If both \(r(x)\) and \(g(x)\) are differentiable, then both are also continuous for all x. The derivative for the product of functions is obtained:
\(h'(x) = r'(x) \cdot g(x) + r(x) \cdot g'(x)\)
\(r'(x) = 2\cdot x\)
\(h'(x) = 2\cdot x \cdot g(x) + (x^{2}+8)\cdot g'(x)\)
Given that \(x = 1\), \(g (1) = -2\) and \(g'(1) = 3\), the derivative of \(h(x)\) evaluated in \(x = 1\) is:
\(h'(1) = 2\cdot (1) \cdot (-2) + (1^{2}+8)\cdot (3)\)
\(h'(1) = 23\)
Find the axis of symmetry of the parabola y=2x^2+4x-1
Answers
Answer:22
Step-by-step explanation:
Add
Multiply
Divide
what is the solution to the inequality 7x^2 + 35x > 42?

Answers
In order to find the solution of this inequality, first let's find its roots:
\(\begin{gathered} 7x^2+35x=42 \\ 7x^2+35x-42=0 \\ x^2+5x-6=0 \\ a=1,b=5,c=-6 \\ \\ x_1=\frac{-b+\sqrt[]{b^2-4ac}}{2a}=\frac{-5+\sqrt[]{25-4\cdot1\cdot(-6)}}{2}=\frac{-5+\sqrt[]{49}}{2}=\frac{-5+7}{2}=1 \\ x_2=\frac{-b-\sqrt[]{b^2-4ac}}{2a}=\frac{-5-7}{2}=-6 \end{gathered}\)The roots are 1 and -6.
Since the concavity of this function is upwards (because a > 0), we have that the function is negative for value of x between the roots and positive for the other values (x < -6 or x > 1).
Since the inequality has the symbol "greater than or equal", we want the positive values, including zero, therefore the answer is x ≤ -6 or x ≥ 1 (option B).
Answer:
\(x < - 6 \ \text{and} \ x > 1\)
Step-by-step explanation:
GivensWe are given an inequality:
\(7x^2 + 35x > 42\)
We are asked to find the solution to this inequality.
SolveFirst, treat this as a quadratic equation. Get the inequality to quadratic form:
\(ax^2+bx+c > 0\\\\7x^2+35x > 42\\\\7x^2+35x-42 > 42-42\\\\7x^2+35x-42 > 0\)
Then, divide both sides by 7:
\(\displaystyle 7x^2+35x-42 > 0\\\\\frac{7x^2+35x-42}{7} > \frac{0}{7}\\\\x^2+5x-6 > 0\)
Then, separate 5x to create a factorable expression. Ask yourself: what two numbers will add up to -6 and multiply to create -6?
\(x^2+5x-6 > 0\\\\x^2+6x-x-6 > 0\)
Then, group the terms together:
\(x^2+6x-x-6 > 0\\\\(x^2+6x)(-x-6) > 0\)
Then, factor out x from the inequality:
\((x^2+6x)(-x-6) > 0\\\\x(x+6)(-x-6) > 0\)
Then, factor out the negative sign from the second part of the expression:
\(x(x+6)(-x-6) > 0\\\\x(x+6)-(x+6) > 0\)
Then, factor out x + 6 from the inequality:
\(x(x+6)-(x+6) > 0\\\\(x+6)(x-1) > 0\)
Then, separate the factors and create two separate inequality sets:
\((x+6)(x-1) > 0\\\\\displaystyle \left \{ {{x+6 > 0} \atop {x-1 > 0}} \right. \\\\\left \{ {{x+6 < 0} \atop {x-1 < 0}} \right.\)
Then, solve the inequalities for x:
\(x+6 > 0\\\\x+6-6 > 0-6\\\\x > -6\\---------------\\x-1 > 0\\\\x-1+1 > 0+1\\\\x > 1\\---------------\\x+6 < 0\\\\x+6-6 < 0-6\\\\x < -6\\---------------\\x-1 < 0\\\\x-1+1 < 0+1\\\\x < 1\)
Then, test each value in the inequality:
\(7x^2+35x > 42\\\\7(-5)^2+35(-5) > 42\\\\7(25)-175 > 42\\\\175-175 > 42\\\\0 \ngtr 42\\\\\text{x} > \text{-6 is not a solution.}\\---------------\\7x^2+35x > 42\\\\7(2)^2+35(2) > 42\\\\7(4)+70 > 42\\\\28+70 > 42\\\\98 > 42\\\\\text{x} > \text{1 is a solution.}\\---------------\)
\(\\7x^2+35x > 42\\\\7(-7)^2+35(-7) > 42\\\\7(49)-245 > 42\\\\343-245 > 42\\\\98 > 42\\\\\text{x} < \text{-6 is a solution.}\\---------------\\7x^2+35x > 42\\\\7(-1)^2+35(-1) > 42\\\\7(1)-35 > 42\\\\7-35 > 42\\\\-28\ngtr42\\\\\text{x} < \text{1 is not a solution.}\)
Final AnswerTherefore, the solutions are x > 1 and x < -6. This means that answer choice A is correct.
Find the area of the trapezoid

Answers
A=((a+b)/2) x h
So if you plug in the variables it will be
A=((9+15)/2) x 20
A=(24/2) x 20
A=12 x 20
A=240
Therefore, the area of the trapezoid is 240 m^2.
hope this helps!!
Answer:
The area of this trapezoid is equal to 240 \(m^{2}\)
Step-by-step explanation:
The area of a trapezoid can be found by using the following formula...
\(Area = \frac{(a + b)h}{2}\) (in this formula a and b are the bases of the trapezoid and h is
the height of the trapezoid).
Now we just substitute the values and get...
\(Area = \frac{(a + b)h}{2} = \frac{(9 + 15)(20)}{2} = \frac{480}{2} = 240m^{2}\)
What is the average
77,78,80
Answers
Answer:
78.3333333333
Step-by-step explanation:
77 + 78 + 80 = 235
235 ÷ 3 = 78.3333333333
Answer:
78.3333
Step-by-step explanation:
add all the numbers and divide by 3(as there are three numbers)
= 77+78+80 3= 235 3= 78.3333The function C(x) represents the cost, in dollars, of renting a bicycle for x hours.
Which statement BEST represents the statement C(5) = 15?
15 bicycles can be rented for 5 hours.
The cost of renting 5 bicycles is 15 dollars.
A
B
C
D
The cost of renting a bicycle for 5 hours is 15 dollars.
The cost of renting a bicycle for 15 hours is 5 dollars.
Answers
The best represents the statement C(5) = 15 is the cost of renting a bicycle for 5 hours is 15 dollars.
What is a function?
A function in mathematics from a set X to a set Y allocates exactly one element of Y to each element of X. The sets X and Y are collectively referred to as the function's domain and codomain, respectively.
Here, we have
Given the function C(x) represents the cost, in dollars, of renting a bicycle for x hours.
So, the best statement that represents the given statement C(5) = 15 is the cost of renting a bicycle for 5 hours is 15 dollars.
To learn more about the function from the given link
https://brainly.com/question/25638609
#SPJ1
Triangle in space with vertices P= (1, 0, 0), Q = (0,1,0), R=(0, 0, 2), find angle at P P=
Answers
Answer:
71.6°
Step-by-step explanation:
The angle can be found from the dot product of PQ and PR.
PQ·PR = |PQ|×|PR|×cos(α)
where α is the angle between the two segments.
cos(α) = (Q -P)·(R -P)/(|Q -P|×|R -P|)
= ((0, 1, 0) -(1, 0, 0))·((0, 0, 2) -(1, 0, 0))/(|Q -P|×|R -P|)
= (-1, 1, 0)·(-1, 0, 2)/(√(((-1)² +1²)((-1²) +2²)) = (1+0+0)/√10
α = arccos(1/√10) ≈ 71.6°
The angle at P is about 71.6°.
_____
Additional comment
The side lengths of the triangle are √2, √5, √5. As we have seen, the angle at P is bounded by the sides of length √2 and √5. The law of cosines can also be used to arrive at the angle between these sides.
Choose the correct description of how the graph of f(x)=x2 changes due to the transformation. Graph the function using your graphing calculator to check your answer. g(x)=−5x2
Answers
The answers are:
B. The graph of f(x) is shifted up 50 units
E. The graph of f(x) is shifted right 10 units
F. The graph of f(x) is reflected over the x-axis
How to calculate transformation?The given function is f(x) = x²
This is an upward-facing vertical parabola.
The vertex is the smallest.
The vertex's origin is at (0, 0).
g(x) = –5x² + 100x – 450
This is an open downhill vertical parabola.
The vertex is the greatest
The first thing to notice is that fx) opens up whereas g(x) opens down, indicating that a reflection across the x-axis was used.
Find the g(x) vertex.
change the form to vertex
g(x) = –5x² + 100x – 450
Complete the square
g(x) = -5(x² - 20x) - 450
g(x) = -5(x² - 20x + 100) - 450 + 500
g(x) = -5(x² - 20x + 100) + 50
g(x) = -5( x - 10)² + 50
The vertex is located at (10, 50).
To the vertex from (0,0) to (10,50)
The translational principle is
(x,y) ------> (x+10,y+50)
This implies ----> The translation is 50 units up and 10 units to the right.
The adjustments are
The f(x) graph is moved forward by 50 units.
The f(x) graph is 10 units to the right.
Over the x-axis is a reflection of the f(x) graph.
To know more about parabola, visit:
https://brainly.com/question/30769006
#SPJ1
The complete question is,
Which transformations have been applied to the graph of f(x) = x² to produce the graph of g(x) = –5x² + 100x – 450? Check all that apply.
A.The graph of f(x) = x² is shifted up 25 units.
B.The graph of f(x) = x² is shifted up 50 units.
C.The graph of f(x) = x² is shifted down 950 units.
D.The graph of f(x) = x² is shifted left 10 units.
E.The graph of f(x) = x² is shifted right 10 units.
F.The graph of f(x) = x² is reflected over the x-axis.
(11 - 8)3 – 2 x 6
What is the answer
Answers
Answer:
15
Step-by-step explanation:
If a coin flipped twenty five times and lands tails up seventeen times, the blank
Probability that the coin lands up is 17/25
