Sketch the Graph for each equation y= | 3x + 5 |
Answers
The Graph of y= |3x+5| is attached below.
We have the Equation:
y= |3x+ 5|
Now, if we plot the equation on the graph we get
Vertex of equation (-1.66, 0)
and, the y intercept (0, 5).
Also, the graph of equation y= |3x+5| is attached below.
Learn more about Graph here:
https://brainly.com/question/17267403
#SPJ1

Related Questions
Raymond has a credit card with a 21.99% Apr. His balance this month is 3,000. Calculate how much interest he will pay this month. Round to the nearest cent.
Answers
The interest Raymond will pay this month is $54.98
What does APR mean?
APR means annual percentage rate, which means that since we are computing monthly interest, the annual rate which is the whole 12 months needs to be divided by 12 to ascertain the equivalent monthly interest rate
monthly interest=21.99%/12
What is the monthly interest amount in dollars?
The monthly interest amount in dollars is determined as the monthly interest rate multiplied by the credit card balance at the end of the month
monthly interest=$3,000*21.99%/12
monthly interest=$54.98
Find out more about credit card balance on:https://brainly.com/question/6872962
#SPJ1
Rewrite in simplest rational exponent form square root of x times the fourth root of x. Show each step of your process.
Answers
Answer:
\( \sqrt[4]{ {x}^{3} } \)
Step-by-step explanation:
\( \sqrt{x} \times \sqrt[4]{x} \\ = {x}^{ \frac{1}{2} } \times {x}^{ \frac{1}{4} } \\ = {x}^{ \frac{1}{2} + \frac{1}{4} } \\ = {x}^{ \frac{3}{4} } \\ = \sqrt[4]{ {x}^{3} } \)
8 ft
10 ft
Find the perimeter of this figure to
the nearest hundredth.
Use 3.14 to approximate .
P = [?] ft
Notice that only half of the circle is included in the figure!
Answers
The perimeter of the figure is 4(π + 9)ft.
What is perimeter?A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length.
Given is a 2 - D figure as shown in the figure attached.
We can write the perimeter as -
P = P{rectangle} + P{semicircle}
P = 2(10 + 8) + (4π)
P = (4π) + (36)
P = 4(π + 9)
Therefore, the perimeter of the figure is 4(π + 9)ft.
To solve more questions on Perimeter, visit the link below -
https://brainly.com/question/14996609
#SPJ1
![8 ft10 ftFind the perimeter of this figure tothe nearest hundredth.Use 3.14 to approximate .P = [?] ftNotice](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/dFiczUV1VJQw8I5GGyu3EvpqmHvY45W3.png)
To find the distance AB across a river, a distance BC=290 is laid off on one side of the river. It is found that B=117degrees and C=24degrees. Find AB.
Answers
The value of distance AB is 187.5 units
What is sine rule?Law of sines defines the ratio of sides of a triangle and their respective sine angles are equivalent to each other.
sine rule can be expressed as;
a/sinA = b/sinB = c/sinC
The opposite side to angle A is BC
the opposite side to angle C is AB
therefore;
A = 180-( 117 +24)
A = 180- 141
A = 39°
290/sin 39 = x/ sin24
xsin39 = 290 × sin24
0.629x = 117.95
x = 117.95/0.629
x = 187.5
therefore the distance AB is 187.5
learn more about sine rule from
https://brainly.com/question/20839703
#SPJ1
f(x) = x³ + 2x - 1, a = -4
(f⁻¹)′( - 4) = ?
Answers
Recall the inverse function theorem. If \(f\) is invertible and differentiable in all the right places, then
\(f^{-1}\bigg(f(x)\bigg) = x \\\\ ~~~~~~~~ \implies \left(f^{-1}\right)'\bigg(f(x)\bigg) f'(x) = 1 \\\\ ~~~~~~~~ \implies \left(f^{-1}\right)'\bigg(f(x)\bigg) = \dfrac1{f'(x)} \\\\ ~~~~~~~~ \implies \left(f^{-1}\right)'(x) = \dfrac1{f'\left(f^{-1}(x)\right)} \\\\ ~~~~~~~~ \implies \left(f^{-1}\right)'(-4) = \dfrac1{f'\left(f^{-1}(-4)\right)}\)
Solve for \(x\) such that \(f(x)=-4\).
\(x^3 + 2x - 1 = -4 \\\\ x^3 + 2x + 3 = 0 \\\\ (x + 1) (x^2 - x + 3) = 0\)
\(x^2-x+3=0\) has non-real solutions, so we're left with
\(x+1 = 0 \implies x = -1\)
Then we have
\(f(-1) = -4 \implies f^{-1}(-4) = -1 \implies \left(f^{-1}\right)' (-4) = \dfrac1{f'(-1)} = \boxed{\dfrac15}\)
since
\(f(x) = x^3 + 2x - 1 \implies f'(x) = 3x^2 + 2 \implies f'(-1)=5\)
FIFO and LIFO Costs Under Perpetual Inventory System The following units of an item were available for sale during the year: Beginning inventory 30 units at $40 Sale 21 units at $62 First purchase 30 units at $42 Sale 19 units at $64 Second purchase 26 units at $44 Sale 23 units at $64 The firm uses the perpetual inventory system, and there are 23 units of the item on hand at the end of the year. a. What is the total cost of the ending inventory according to FIFO? $fill in the blank 1 b. What is the total cost of the ending inventory according to LIFO?
Answers
The ending inventory using LIFO is $920.
The ending inventory using FIFO is $1,472.
What is the ending inventory?
LIFO means last in first out. It means that it is the last purchased inventory that is the first to be sold. Ending inventory would consist of first purchased inventory.
23 x $40 = $920
FIFO means first in, first out. It means that it is the first purchased inventory that is the first to be sold. Ending inventory would consist of last purchased items in inventory.
23 x $64 = $1,472
To learn more about FIFO, please check: https://brainly.com/question/294129
#SPJ1
7+12x=103 show how you checked it was right
Answers
Answer:
x=8. You plug 8 in for x.
7+12(8)=103
7+96=103
Step-by-step explanation:
7+12x=103
or 12x=103-7
x=96/12=8
to check it 8 is needed.
7+12×8=103
Solve the inequality and enter your solution as an inequality in the box below,
using "<=" for sor">=' for if necessary.
-2(5x + 1) > 48
Answers
Answer:
x < -5
Step-by-step explanation:
-2(5x+1) >48
-10x-2 > 48
-10x-2+2 > 48+2
-10x > 50
p.s : when dividing by a negative number with inequalities, change the sign, i.e. < would then be >....
therefore:
x < -5
10z^2 -2z-2 10z 2 −2z−2
Answers
z =(2-√-116)/-20=1/-10+i/10√ 29 = -0.1000-0.5385i
z =(2+√-116)/-20=1/-10-i/10√ 29 = -0.1000+0.5385i
Step-by-step explanation:
Yoko, Austin, and Tom sent a total of 96 text messages over their cell phones during the weekend. Tom sent 3 times as many messages as Austin. Austin sent 6 fewer messages than Yoko. How many messages did they each send? Number of text messages Yoko sent: Number of text messages Austin sent: Number of text messages Tom sent:
Answers
Solution
Given that:
Total number of messages sent is 96
Let the number of messages Yoko sent be x
=> Austin will send x - 6 (since austin sent 6 fewer messages)
=> Tom will send 3(x - 6) (since Tom sent 3 times as many messages)
Since they make a total of 96
\(\begin{gathered} \Rightarrow x+x-6+3(x-6)=96 \\ \\ \Rightarrow x+x-6+3x-18=96 \\ \\ \Rightarrow5x-24=96 \\ \\ \Rightarrow5x=96+24 \\ \\ \Rightarrow5x=120 \\ \\ \Rightarrow x=\frac{120}{5} \\ \\ \Rightarrow x=24 \end{gathered}\)Hence, Yoko sent: 24 messages
Austin sent: 24 - 6 = 18 messages
Tom sent: 3(18) = 54 messanges
Number of text messages Yoko sent: 24 messages
Number of text messages Austin sent: 18 messages
Number of text messages Tom sent: 54 messanges
If the sum of two numbers is 4 and the sum of their squares minus three times their product is 76, find the numbers.
Answers
I'll be referring to each of these numbers as x and y.
x + y = 4
(x^2) + (y^2) - 3(x)(y) = 76
x = 4 - y
(4 - y)^2 + (y^2) - 3(4 - y)(y) = 76
(4 - y)(4 - y) + y^2 - (3y)(4 - y) = 76
16 - 4y - 4y + y^2 + y^2 - 12y + 3y^2 = 76
16 - 20y + 5y^2 = 76
5y^2 - 20y - 60 = 0
y^2 - 4y - 12y = 0
(y - 6)(y + 2) = 0
y = 6 or -2
x = 4 - 6 = -2
x = 4 - - 2 = 6
As you can see, we got the same numbers for both x and y, -2 and 6. Therefore, the two numbers are -2 and 6. But, we can check our work to ensure that the answer is correct.
x = -2
y = 6
6 - 2 = 4
4 = 4
(-2)^2 + (6^2) - 3(-2)(6) = 76
4 + 36 - 3(-12) = 76
40 + 36 = 76
76 = 76
Hope this helps!
Answer:
X and y = -2 or 6
Step-by-step explanation:

Find the value of x the is a geometry question please help

Answers
Answer:
x = 17
Step-by-step explanation:
In order to make any sense of this problem, we must assume the lines that look parallel are parallel. With that assumption, the two marked angles are supplementary:
61° +7x° = 180°
7x = 119 . . . . . . . subtract 61°, divide by °
x = 17 . . . . . . . . divide by 7
NO LINKS!!!
answer all 3!!!!
easy brainliest!!



Answers
Answer:
Step-by-step explanation:
1) DE = 6/sin63 = 6.7
DF = 6/tan63 = 3.1
m∠E = 180 - 90 - 63 = 27°
2) tan30 = 1/√3 = UV / (27√10)
UV = (27√10) / √3 · (√3/√3) = (27√30) / 3 = 9√30
3) cosV = 3/8
cos⁻¹(3/8) = 68
m∠V = 68°
A rare baseball card that was purchased increases in value over time. The function C(t) is represented on the following graph, where C represents the value of the card, and t is time in years since the card was purchased.
What is the initial value, and what does it represent?
Select the statement that answers both parts of the question correctly.
The initial value is 0 and it represents the lowest value of the card.
The initial value is 10 and it represents the amount of time it takes for the card to increase in value.
The initial value is 12,000 and it represents the price of the baseball card at the time of purchase.
The initial value is 12,000 and it represents the price of the card when it was new.

Answers
Answer: The initial value is 12,000 and it represents the price of the baseball card at the time of purchase.
Explanation: I just looked at the beginning of the graph, surprisingly I got it right.
Initial value is 12,000 and it represents the price of the baseball card at the time of purchase.
What is Graph?Graph is a mathematical representation of a network and it describes the relationship between lines and points.
Given,
The function C(t) is represented on the following graph, where C represents the value of the card, and t is time in years since the card was purchased.
We need to find the initial value and we have to select the statement which is true.
The initial value is 0 and it represents the lowest value of the card.
The initial value is 10 and it represents the amount of time it takes for the card to increase in value.
The initial value is 12,000 and it represents the price of the card when it was new.
Among the given statements, the 4th statement is true based on the graph.
Hence initial value is 12,000 and it represents the price of the baseball card at the time of purchase.
To learn more on Graphs click:
https://brainly.com/question/17267403
#SPJ2
lee is traveling by train. he has 270 miles left to travel.after 2 hours,he has 180 miles remaining.the train travels at a constant rate for the entire trip.what is the speed of the train and the distance of the trip?
Answers
The following sequence is a geometric sequence
17
,
51
,
153
,
459
,
1377
,
...
Find the sum of the first 13 terms of this sequence.
What is the common ratio for this sequence?
r
=
What is the index of the final term of this sum?
last index =
What is the sum?
Sum =
Answers
Answer:
13,551,737
Step-by-step explanation:
You want the sum of the first 13 terms of the geometric sequence with first term 17, and successive terms 51, 153, ....
Common ratioThe common ratio is found by dividing a sequence term by the one before it:
r = 51/17 = 3
The common ratio is 3.
IndexThe index of the 13th term of the sequence is n = 13.
SumThe sum of n terms of a geometric sequence with first term a1 and common ratio r is ...
Sn = a1·(r^n -1)/(r -1)
For a1 = 17, r = 3, and n = 13, the sum is ...
\(S_{13}=17\cdot\dfrac{3^{13}-1}{3-1}=17\cdot\dfrac{1594322}{2}=\boxed{13,\!551,\!737}\)
using the disk method, determine the volume of a solid formed by revolving the region bounded above by the line , on the left by the line , on the right by the curve , and below by the line the about the -axis.
Answers
The volume of a solid formed by revolving the region bounded above by the line is (932π/15)
To use the disk method, we need to integrate over the axis of revolution, which is the y-axis in this case. We can break the solid into vertical disks of thickness dy.
The radius of each disk is given by the distance between the y-axis and the curve \(x = y^2 - 1\). So the radius is:
\(r = y^2 - 1\)
The height of each disk is the difference between the y-coordinate of the top curve y = 3 and the y-coordinate of the bottom curve y = 1. So the height is:
h = 3 - 1 = 2
The volume of each disk is then:
\(dV = \pi r^2h dy\)
Substituting r and h, we have:
\(dV = \pi (y^2 - 1)^2 (2) dy\)
To find the total volume, we integrate over the range of y from 1 to 3:
\(V = \int_{1}^{3} \pi(y^2 - 1)^2 (2) dy\)
This integral can be simplified by expanding the squared term:
\(V = \int_{1}^{3} \pi (y^4 - 2y^2 + 1) (2) dyV = 2\pi \int_{1}^{3}(y^4 - 2y^2 + 1) dyV = 2\pi [(1/5)y^5 - (2/3)y^3 + y]^3_1\)
V = \(2\pi [(1/5)(3^5 - 1^5) - (2/3)(3^3 - 1^3) + (3 - 1)]\)
V = 2π [(1/5)(242) - (2/3)(26) + 2]
V = 2π [(242/5) - (52/3) + 2]
V = 2π [(726/15) - (260/15) + 30/15]
V = 2π [(466/15)]
V = (932π/15)
To learn more about Disk method :
https://brainly.com/question/29891838
#SPJ4
Note: The full question is
Use the disk method or the shell method to find the volumes of the solids generated by revolving the region bounded by the graphs of the equations about the given lines. y = 1, y = 3, x = y^2 - 1.
What is the measure
Pls help i will give brainliest
Picture included

Answers
100 is your answer
Hope this helps!
Please help me on this question. Thanks

Answers
Answer:
E. p - 7 + 7 = 22 + 7
Step-by-step explanation:
p - 7 + 7 = 22 + 7 ( -7 + 7 = 0)
p = 22 + 7
p - 7 = 22//
Based on the family the graph below belongs to, which equation could represent the graph? image below.
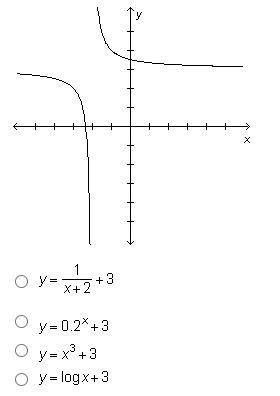
Answers
Answer:
y = 1/x+2 + 3
Step-by-step explanation:
x = -2
y = 3
A rectangular tank measuring 40 cm long, 30 cm wide and 35 cm high was filled with water to a hight of 15 cm. 4800 cm3 of water were poured into water. find the new height of water
answer ASAP
Answers
The volume of the rectangular tank is:
V = l × w × h = 40 cm × 30 cm × 35 cm = 42,000 cm³
The initial volume of water in the tank is:
V1 = l × w × h1 = 40 cm × 30 cm × 15 cm = 18,000 cm³
When 4800 cm³ of water is poured into the tank, the new volume of water becomes:
V2 = V1 + 4800 cm³ = 18,000 cm³ + 4800 cm³ = 23,800 cm³
Let's assume that the new water height is h2 cm. We can use the formula for the volume of a rectangular tank to find the new height:
V = l × w × h2
h2 = V / (l × w) = (23,800 cm³) / (40 cm × 30 cm) ≈ 19.83 cm
Therefore, the new height of the water in the tank is approximately 19.83 cm.
What percentage of the individuals rode the Ferris wheel and did not ride the roller coaster?

Answers
Answer:
B and D
Step-by-step explanation:
they both make srnse to me
The required percentage of individuals is 66.07%.
What is percentage?
A percentage is a value that indicates 100th part of any quantity.
A percentage can be converted into a fraction or a decimal by dividing it by 100.
The required data from the given table is as follows,
The total number of individuals is 112.
The number of individuals who ride Ferris wheel but not roller coaster is 74.
As per the question the percentage can be found as below,
Required percent = (The required number ÷ Total number) × 100
= (74 ÷ 112) × 100%
= 66.07%
Hence, the percentage of the individuals rode the Ferris wheel and did not ride the roller coaster is 66.07%.
To know more about percentage click on,
brainly.com/question/29306119
#SPJ2
How is your day? I hope you had a great one!
Answers
Answer:
great!
Step-by-step explanation:
how about you?
Jffkdjdjdjdkskkskskskskakskkdkdkskdk

Answers
Answer:
the anser is d
Step-by-step explanation:
Answer:
b) 7x² - 12x√14 + 72
Step-by-step explanation:
Let's solve the problem,
→ (x√7 - 3√8)(x√7 - 3√8)
→ (x√7 - 3√8)²
→ 7x² - 12x√14 + 72
Hence, option (b) is correct.
Please help
will mark BRAINLIEST

Answers
The angle sum property of a triangle and the angle formed between a tangent and a radius of a circle indicates.
m∠ADC = 58°
What is a tangent to a circle?A tangent to a circle is a straight line which touches the circumference of a circle at only one point.
The vertical angles theorem indicates that we get;
∠1 ≅ ∠2
Therefore; m∠1 = m∠2
The tangent to a circle indicates that we get;
The angle formed at vertex B and Q are 90 degrees angles and the triangles ABP and AQP are right triangles, which indicates that the acute angles of each of the right triangles are complementary, therefore;
m∠1 + 26° = 90°
m∠1 = 90° - 26° = 64°
Therefore, m∠2 = m∠1 = 64°
m∠2 = m∠CAD = 64°
The segments AC and AD are radial lengths therefore, the triangle ΔACD is an isosceles triangle.
m∠ADC ≅ m∠ACD (Base angles of an isosceles triangle)
The angles ∠ADC and ∠ACD are therefore;
m∠CAD + m∠ADC + m∠ACD = 180° (Angle sum property of a triangle)
m∠CAD + m∠ADC + m∠ADC = 180°
m∠CAD + 2 × m∠ADC = 180°
64° + 2 × m∠ADC = 180°
m∠ADC = (180° - 64°)/2 = 58°
m∠ADC = 58°
Learn more on the angle sum property of a triangle here: https://brainly.com/question/22262639
#SPJ1
PLEASE HELP!!!
The variables y and x have a proportional relationship, and y = 9 when x = 2.
What is the value of y when x = 3?
Enter your answer as a decimal in the box.
Answers
When value of x is given as 3 then according to the said proportional relationship y will be 13.15.
How can we explain it ?We are given that y and x have a proportional relationship, and y = 9 when x = 2. This means that there is a constant of proportionality, k, such that y = kx.
We can use the information given to find the value of k:
y = kx
9 = k(2)
k = 9/2
Now that we know the value of k, we can use it to find the value of y when x = 3:
y = kx
y = (9/2) * 3
y = 13.5
So the value of y when x = 3 is 13.5
What are ratios ?A ratio is a way of comparing two or more values or quantities. It is a mathematical expression that shows the relationship between different values, typically by using the symbol ":" to separate the values. For example, if we have three apples and two oranges, we can express the relationship between the apples and oranges as a ratio 3:2. Ratios can also be written as fractions, in this case the ratio 3:2 can be written as 3/2.
Learn more about Percentages here.
https://brainly.com/question/29116686
#SPJ1
Please help! I will mark brainliest if your correct!

Answers
The roof top would be 0. At 12 seconds the ball is at -225.6, which would be the ground so the building would be 225.6 meters tall.
The highest positive value is 81.6, so this is the highest the ball goes up.
The value changes from a positive to a negative between 8 and 10, which means that would be around the time it is the same height as the building.
The answers would be:
The first and third choices
Which equations can be used to find the lengths of the legs of the triangle? Select three options. 0.5(x)(x + 2) = 24 x(x + 2) = 24 x2 + 2x – 24 = 0 x2 + 2x – 48 = 0 x2 + (x + 2)2 = 100
Answers
The equations that can be used to find the lengths of the legs of the triangle are as follows:
100 = (x + 2)² + x²24 = 0.5 × (x + 2)(x)x² + 2x - 48 = 0How to find the equation of a right triangle?The equation that can be used to find the length of the leg of the right triangle uses Pythagoras theorem,
Therefore,
c² = a² + b²
where
c = hypotenuse sidea and b are the other legsTherefore,
10² = (x + 2)² + x²
100 = (x + 2)² + x²
Therefore, using the area of a triangle,
area of a triangle = 1 / 2 bh
where
b = baseh = heightTherefore,
area of the triangle = 1 / 2 × (x + 2)(x)
24 = 0.5 × (x + 2)(x)
24 = x² + 2x / 2
cross multiply
48 = x² + 2x
x² + 2x - 48 = 0
learn more on equation here: https://brainly.com/question/14992132
#SPJ1

What is the surface area of the image below I’ll give b brainliest

Answers
Answer:
50(5π + 6) cm²
Step-by-step explanation:
TSA of figure = 1/2 of TSA(Cylinder) + Area of rectangle
= 1/2 of 2πr(h+r) + 20*15
= πr(h+r) + 300
= 10π(15+10) + 300
= 250π + 300 cm²
or 50(5π + 6) cm²
Dawn spent $26.50, including sales tax, on 4 books and 3 folders. The books cost $5.33 each and the total sales tax was $1.73.
How much was each folder?
Explain your process and justify your reasoning.
Answers
Answer:
1.15
Step-by-step explanation:
26.50-1.73= 24.77
Each book was 5.33 and since there was 4 of them:
5.33 x 4 = 21.32
We subtract from the original answer
24.77- 21.32 = 3.45
3.45/3 = 1.15
Hope this makes sense
I had this question