solve 3x+4y=17
5x+4y=27
Answers
Answer:
(5x+4y)-(3x+4y)=27-17
2x=10
x=10÷2
=5
Answer:
x = 5, y = 1/2
Step-by-step explanation:
-3x - 4y = -17 Use the elimination method by adding the 2 equations together
5x+4y=27
2x = 10 ===> x = 5
3(5) + 4y = 17,
4y = 2 ===> y = 1/2
Related Questions
Subtract. Write your answer in simplest form. 8/13 - 2/13
Answers
Answer: 6/13
Step-by-step explanation:
6/13 is the simplest form
Answer:
Hi buddy
Step-by-step explanation:
step 1: just simply subtract the numerators because the denominators are the like numbers
:8-2=6
step 2 the answer is
6/13
NOTE: there Is no simple form because there is no simple form for 13
# continue learning #pls Mark me as the brainliestA perimeter of a square field is 20cm. what is the area of the field?
Select one:
a. 25cm2
b. 16cm2
c. 12cm2
d. 48cm2
Answers
The area will be 25cm²
HOPE IT HELPS YOU♡♡
Translate this phrase into an algebraic expression.
Seven more than the product of 20 and Carlos's savings
Use the variable C to represent Carlos's savings.
Answers
20c +9 is use the variable C to represent Carlos's savings.
What is simple solution to a variable?
A variable is a quantity that can be altered depending on the mathematical issue. The general letters that are utilized in many algebraic expressions and equations are x, y, and z.
To put it another way, a variable is a symbol for a numeric value for which there is no known value. In this case, x + 5 = 10. "X" in this case is a variable.
Product is multiplication.
The product of 20 and Chau's score would be written as 20c
Then you want 9 more, so you would add 9 at the end to get
20c +9
Learn more about variable
brainly.com/question/17344045
#SPJ1
a 3-ary tree is the tree in which every internal node has exactly 3 children. how many leaf nodes are there in a 3-are tree with 6 internal nodes
Answers
A 3-ary tree is a tree in which each internal node has exactly three children, there are 1086 leaf nodes in a 3-ary tree with 6 internal nodes.
What is the number of leaf nodes in a 3-ary tree with six internal nodes?For a 3-ary tree with 6 internal nodes, there will be a total of 7 levels (0 to 6). Consider the following formula for the number of nodes in a tree of height\(h: n = 1 + 3 + 3^2 + 3^ + ... + 3^h\) The given 3-ary tree has a height of 6, so its number of nodes is:\(n = 1 + 3 + 3^2 + 3^3 + 3^4 + 3^5 + 3^6\)
Using the geometric series formula, we can simplify this: \(n = (3^7 - 1) / 2n = (2186 - 1) / 2n = 1092\) The number of leaf nodes in a 3-ary tree with 6 internal nodes is:\(n - 6n - 6 = 1092 - 6n - 6 = 1086\) Therefore, there are 1086 leaf nodes in a 3-ary tree with 6 internal nodes.
See more about internal nodes at: https://brainly.com/question/29608280
#SPJ11
The four small circles are identical. The total area of the small circles is 36π square inches. What is the area of the larger circle?

Answers
Answer:
Check pdf
Step-by-step explanation:
The radius of the larger circle is 12 inches. Then the area of the larger circle will be 144π square inches.
What is the area of the circle?Let r be the radius of the circle. Then the area of the circle will be
A = πr² square units
The four small circles are identical. The total area of the small circles is 36π square inches. Then the radius of each small circle is given as,
36π = 4 × (πr²)
r² = 9
r = 3 inches
Then the radius of the larger circle is calculated as,
R = 4r
R = 4 × 3
R = 12
Then the area of the larger circle will be given as,
A = π × (12)²
A = 144π square inches
The radius of the larger circle is 12 inches. Then the area of the larger circle will be 144π square inches.
More about the area of a circle link is given below.
https://brainly.com/question/11952845
#SPJ2
Jill has a piece of aluminum. The aluminum hass a mass of 5.4g and a volume of 2cm^3. What is the density of the aluminum?
Answers
mass (m) = 5.4g
Volume (V) = 2 cm^3
To find the density (p), we have to apply the next formula:
p= m/v
Replacing:
p´= 5.4/2 = 2.7 g/cm^3
MP Reason Abstractly If y varies directly with x-
direct variation. Then find each value.
9. If y = 14 when x = 8, find y when x = 12.
Answers
I need a hard 8th-grade math question (ON LEVEL) please don't give me the answer also tell me how I can use it in real life
Answers
35 mm
10 cm
20 mm
45 mm
If the original ordered pair in a shape was ( 3, 4), what would the new ordered pair be after a Dilation with a scale factor of 2 ?
Answers
Answer:
(6, 8 )
Step-by-step explanation:
Assuming the dilatation is centred at the origin, then multiply the coordinates by the scale factor 2, that is
(3, 4 ) → (2(3) , 2(4) ) → (6, 8 )
PLS HELP I NEED AN A - 10 PTS AND BRAINLIEST FOR RIGHT ANSWER

Answers
Answer:
Well, count out how many nickels can go in $3.90. Then count out how many quarters. Make sure there are 6 more quarters than nickels, and make sure it all adds up to $3.90
Hope this helped! <3
Please answer this question now in two minutes
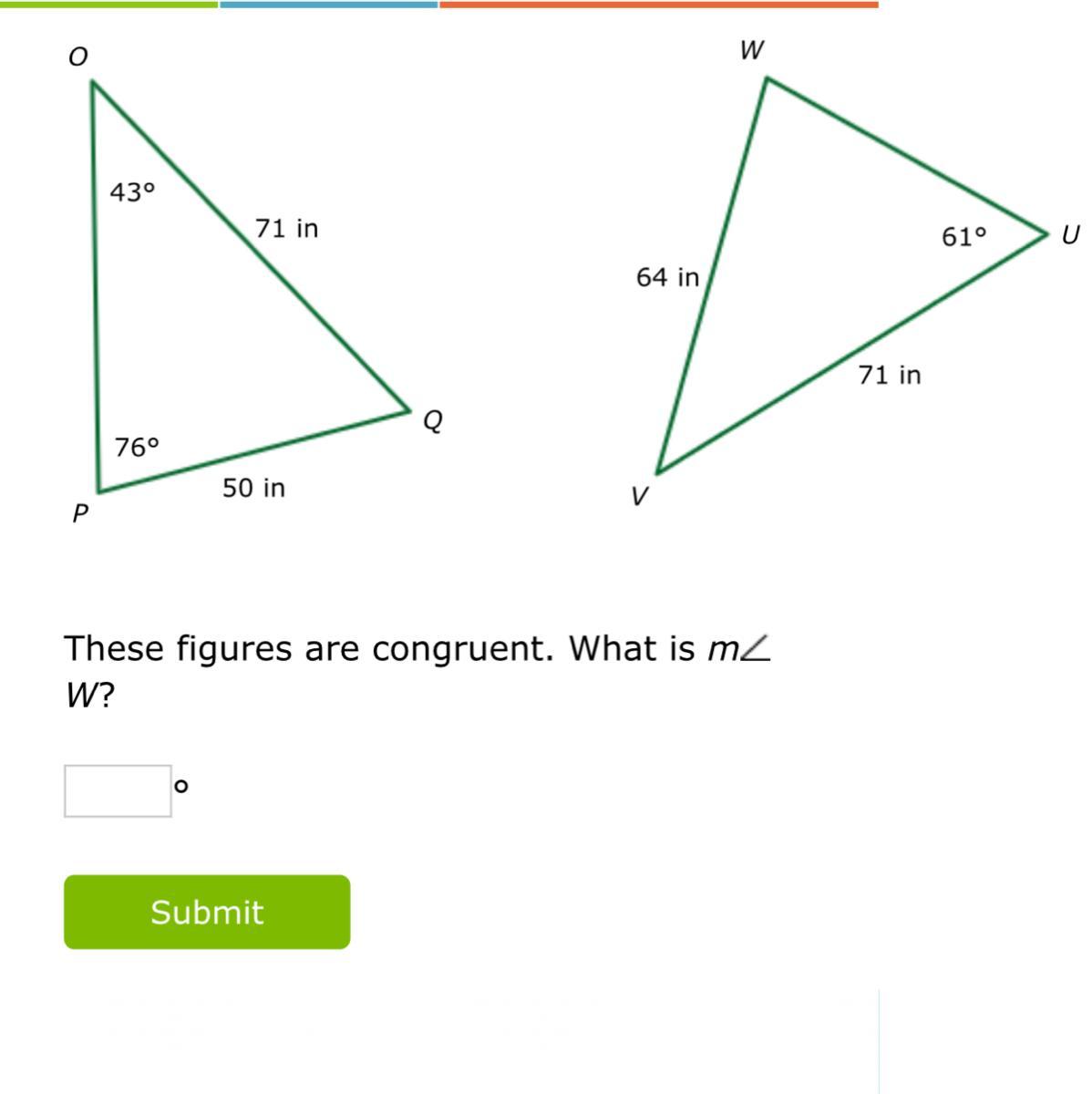
Answers
Answer:
76
Step-by-step explanation:
to check if add all angles and see if they add to 180,
then find the sides that are congruent
Solve each system of equations algebraically. y=x + 15, y= 2x
Answers
The solution to the system of equations is (15, 30).
What is system of equations?A group of two or more equations that must be solved all at once is known as a system of equations. The system's equations each show how two or more variables relate to one another. The variables' values that satisfy every equation in the system can be discovered using algebraic techniques.
Algebraic systems of equations can be solved using a variety of techniques, such as substitution, elimination, and graphing. The substitution approach involves solving one equation for one variable in terms of the other variable, and then substituting the result for that variable's expression into the other equation.
The given system of equations are y=x + 15, y= 2x.
Substitute the value of y from equation 2 in equation 1:
x + 15 = 2x
15 = x
Substitute the value of x to get the value of y:
y = 2x = 2(15) = 30
Hence, the solution to the system of equations is (15, 30).
Learn more about system of equations here:
https://brainly.com/question/13760328
#SPJ1
2 1/2 = 5n
I need help please
Answers
Answer:
1/2
Step-by-step explanation:
because 5 times 1/2 and you get 2 1/2
Why can the sine ratio never be greater than 1?
Answers
Because the sine and cosine ratios involve dividing a leg (one of the shorter two sides) by the hypotenuse (the longest side), the ratio values will never be greater than one, because (some number) / (a larger number) is always less than one.
What is sine and cosine?Sine & cosine are trigonometric functions of an angle in mathematics. In the context of a right triangle, the sine and cosine of an acute angle are defined as follows: for the specified angle, the sine is the ratio of the length of the side opposite that angle to the length of the triangle's longest side (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse.
The sine and cosine functions for an angle θ are simply denoted as sin θ and cos θ. In general, the definitions of sine and cosine can be extended to any real value expressed in terms of the lengths of specific line segments in a unit circle.
Learn more about sine and cosine
https://brainly.com/question/13813821
#SPJ4
Shane, Cheryl, and Isaac went to the store to buy school supplies. Shane bought 4 pens, 3 folders, and 2 notebooks for a total of $12.25. Cheryl bought 4 folders and 6 notebooks for a total of $22. Isaiah bought 2 pens, 1 folder, and 3 notebooks for a total of $10.25. How much does each supply cost? Each pen costs $(1.25 0.50 0.75 1.75). Each folder costs $(2.75 1.75 2.50 1.25). Each notebook costs $(2.75 1.75 2.50 1.25).
Answers
The cost of each entity: each pen is $\(1.75\), each folder is $\(2.50\), and each notebook is $\(1.75\).
Let's assign variables to the costs of each supply:
Let the cost of each pen be P dollars.
Let the cost of each folder be F dollars.
Let the cost of each notebook be N dollars.
According to the given information, we can form the following equations:
For Shane:
\(4P + 3F + 2N = 12.25 (Equation \ 1)\)
For Cheryl:
\(4F + 6N = 22 (Equation \ 2)\)
For Isaiah:
\(2P + F + 3N = 10.25 (Equation \ 3)\)
To solve this system of equations, we can use substitution or elimination method.
Using the elimination method, let's multiply Equation 2 by 2 and Equation 3 by 4 to eliminate F:
\(8F + 12N = 44 (Equation \ 4)\\8P + 2F + 12N = 41 (Equation \ 5)\)
Now, subtract Equation 4 from Equation 5 to eliminate F:
\(8P + 2F + 12N - (8F + 12N) = 41 - 44\\8P - 6F = -3\)
Simplifying further, we have:
\(8P - 6F = -3 (Equation \ 6)\)
Now, let's multiply Equation 1 by 4 and Equation 3 by 3 to eliminate N:
\(16P + 12F + 8N = 49 (Equation \ 7)\\6P + 3F + 9N = 30 (Equation \ 8)\)
Now, subtract Equation 8 from Equation 7 to eliminate N:
\(16P + 12F + 8N - (6P + 3F + 9N) = 49 - 30\\10P + 9F - N = 19\)
Simplifying further, we have:
\(10P + 9F - N = 19 (Equation \ 9)\)
Now we have a system of equations consisting of Equation 6, Equation 9, and Equation 2:
\(8P - 6F = -3 (Equation \ 6)\\10P + 9F - N = 19 (Equation \ 9)\\4F + 6N = 22 (Equation \ 2)\)
To find the values of P, F, and N, we can solve this system of equations using any suitable method, such as substitution or elimination.
For more such questions on cost of each entity:
https://brainly.com/question/22097711
#SPJ8
PLEASEEE HELPPP!!!!!!!! 50 POINTSSSSSS
(x+5i)(x-5i)(x-3-i)(x-3+i)
Answers
Answer:
\(x^{4}\) - 6x³ + 35x² - 150x + 250
Step-by-step explanation:
note that i² = - 1
(x + 5i)(x - 5i)(x - 3 - i)(x - 3 + i) ← expand the first pair of factors using FOIL
= ( x² - 5ix + 5ix - 25i²)((x - 3) - i)((x - 3) + i) ← expand second pair using FOIL
= (x² - 25(- 1))((x - 3)²+ i(x - 3) - i(x - 3) - i²)
= (x² + 25)(x² - 6x + 9 - (- 1))
= (x² + 25)(x² - 6x + 9 + 1)
= (x² + 25)(x² - 6x + 10)
each term in the second factor is multiplied by each term in the first factor
= x²(x² - 6x + 10) + 25(x² - 6x + 10) ← distribute parenthesis
= \(x^{4}\) - 6x³ + 10x² + 25x² - 150x + 250 ← collect like terms
= \(x^{4}\) - 6x³ + 35x² - 150x + 250
$10,000 is what percent of $10,000?
Ples help me
Answers
Answer:
100%
Step-by-step explanation:
Answer:
100 percent
Step-by-step explanation:
This is very easy. Try learning it yourself as when you'll grow the stuff you are learning now will be essential to your learning. Your future learning depends on it.
30 points
Findlay spun the lucky wheel. The lucky wheel is divided into 9 sectors of equal size lettered A through I.
What is P(vowel or D)?

Answers
The probability of vowel or letter D is determined as 4/9.
What is P(vowel or D)?The probability of vowel or letter D is calculated by applying the formula for probability of an event as follows;
Mathematically, the formula for probability is given as;
P (E) = number of outcomes in event E / total number of outcomes in sample space
If the lucky wheel is divided into 9 sectors of equal size lettered A through I, the number of outcomes include the following;
number of outcomes = A, B, C, D, E, F, G, H, I
vowels in the outcome = A, E, I
letter D in the outcome = D
number of outcomes = {A, E, I} or {D}
P(vowel or D) = 3/9 or 1/9
P(vowel or D) = 3/9 + 1/9
P(vowel or D) = 1/3 + 1/9
P(vowel or D) = 4/9
Learn more about probability here: https://brainly.com/question/25870256
#SPJ1
Factor the polynomial
HELPPP I NEED THIS DUE ASAP

Answers
Answer:
Tony is not correct because 3(x^2-25) can be factored further. The final answer is 3(x+5)(x-5)
Step-by-step explanation:
finally answer
If a simple machine requires an effort of 20 newtons to lift a load of 100 newtons, its
mechanical advantage is:
a. 5
b. 5N
c. 5MA
Answers
Answer:
A. 5
Step-by-step explanation:
Hope this helps!
Suppose we want to prove the following using a proof by contraposition: Any natural number x that is divisible by 4 is even. With what assumption(s) could you start your proof? x is an arbitrary natural number that is not even x is an arbitrary natural number that is divisible by 4 and not even x is an arbitrary natural number that is odd x=4 x is an arbitrary even natural number x is an arbitrary natural number divisible by 4
Answers
To start a proof by contraposition, we need to assume the negation of the conclusion and then try to prove the negation of the premise.
In this case, the conclusion is "x is even" and the premise is "x is divisible by 4."
So, we should start with the assumption that x is an arbitrary natural number that is not even. This is the negation of the conclusion. From this assumption, we will try to prove that x is not divisible by 4, which is the negation of the premise.
Therefore, the correct assumption to start the proof by contraposition is: "x is an arbitrary natural number that is not even."
The other options are incorrect because they do not correctly negate the conclusion or the premise.
For example, "x is an arbitrary natural number that is divisible by 4 and not even" is not the negation of the conclusion, and "x is an arbitrary natural number that is odd" is not the negation of the premise.
To know more about contraposition click on below link:
https://brainly.com/question/5306301#
#SPJ11
During lunchtime, customers arrive at a postal office at a rate of = 36 per hour. The interarrival time of the arrival process can be approximated with an exponential distribution. Customers can be served by the postal office at a rate of = 45 per hour. The system has a single server. The service time for the customers can also be approximated with an exponential distribution.
What is the probability that at most 4 customers arrive within a 5-minute period? You can use Excel to calculate P(X<=x). What is the probability that the service time will be less than or equal to 30 seconds? You can use Excel to calculate P(T<=t). (Round your answer to four decimals)
Answers
The probability that at most 4 customers arrive within a 5-minute period is approximately 0.128 and the probability that the service time will be less than or equal to 30 seconds is 0.5276.
Given that during lunchtime, customers arrive at a postal office at a rate of 36 per hour. The interarrival time of the arrival process can be approximated with an exponential distribution. Customers can be served by the postal office at a rate of 45 per hour. The system has a single server. The service time for the customers can also be approximated with an exponential distribution.
We need to calculate the probability that at most 4 customers arrive within a 5-minute period.
We know that,
λ = 36 customers per hour
So, μ = 36 customers per 60 minutes
= 0.6 customers per minute
P(X ≤ 4) = P(0) + P(1) + P(2) + P(3) + P(4)
= e^-λ + λe^-λ + (λ^2 / 2)e^-λ + (λ^3 / 6)e^-λ + (λ^4 / 24)e^-λ
= e^-36 (1 + 36 + (36^2 / 2) + (36^3 / 6) + (36^4 / 24))≈ 0.128
We need to calculate the probability that the service time will be less than or equal to 30 seconds.
We know that,
μ = 45 customers per hour
= 0.75 customers per minute
P(T ≤ 30 seconds) = P(T ≤ 0.5 minutes)
= 1 - e^-μT
= service time
= 30 seconds
= 0.5 minutes
∴ P(T ≤ 0.5)
= 1 - e^-0.75
= 1 - 0.4724
= 0.5276
Hence, the probability that at most 4 customers arrive within a 5-minute period is approximately 0.128 and the probability that the service time will be less than or equal to 30 seconds is 0.5276.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
Using vertex form write an equation for the parabola that passes through the point ( 2 , 5 ) and has a vertex ( 1 , 3 ).
Answers
The equation of the parabola is y = 2(x - 1)² + 3
How to determine the equation of the parabola?From the question, we have the following parameters that can be used in our computation:
Vertex = (1. 3)
Point = (2, 5)
These parameters can be expressed as
(h, k) = (1, 3)
(x, y) = (2. 5)
A parabola can be represented as
y = a(x - h)² + k
Substitute the known values in the above equation, so, we have the following representation
y = a(x - 1)² + 3
Next, we have
5 = a(2 - 1)² + 3
Evaluate the difference and the exponent
5 = a + 3
So, we have
a = 2
Substitute a = 2 in y = a(x - 1)² + 3
y = 2(x - 1)² + 3
Hence, the equation is y = 2(x - 1)² + 3
Read more about parabola at
https://brainly.com/question/1480401
#SPJ1
a particle moves in a straight line with the given velocity ()=6cos() (in m/s).v(t)=6cos(t) (in m/s). find the displacement and distance traveled over the time interval [0,5].[0,5π].
Answers
The displacement and distance traveled depend on the given time interval.
To find the displacement, we need to integrate the velocity function from 0 to 5 or 0 to 5π, depending on the given time interval.
If the time interval is [0,5], we have:
Displacement = ∫[0,5] v(t) dt
Displacement = ∫[0,5] 6cos(t) dt
Displacement = [6sin(t)] from 0 to 5
Displacement = 6sin(5) - 6sin(0)
Displacement ≈ 2.785 meters
If the time interval is [0,5π], we have:
Displacement = ∫[0,5π] v(t) dt
Displacement = ∫[0,5π] 6cos(t) dt
Displacement = [6sin(t)] from 0 to 5π
Displacement = 0 - 6sin(0)
Displacement = 0 meters
To find the distance traveled, we need to integrate the absolute value of the velocity function over the given time interval.
If the time interval is [0,5], we have:
Distance = ∫[0,5] |v(t)| dt
Distance = ∫[0,5] |6cos(t)| dt
Distance = ∫[0,π/2] 6cos(t) dt + ∫[π/2,5] -6cos(t) dt
Distance = [6sin(t)] from 0 to π/2 + [-6sin(t)] from π/2 to 5
Distance = 6 - 6sin(5) ≈ 2.215 meters
If the time interval is [0,5π], we have:
Distance = ∫[0,5π] |v(t)| dt
Distance = ∫[0,5π] |6cos(t)| dt
Distance = ∫[0,π] 6cos(t) dt + ∫[π,2π] -6cos(t) dt + ∫[2π,3π] 6cos(t) dt + ∫[3π,4π] -6cos(t) dt + ∫[4π,5π] 6cos(t) dt
Distance = [6sin(t)] from 0 to π + [-6sin(t)] from π to 2π + [6sin(t)] from 2π to 3π + [-6sin(t)] from 3π to 4π + [6sin(t)] from 4π to 5π
Distance = 0 meters
Know more about displacement here;
https://brainly.com/question/30087445
#SPJ11
solve the equation for the indicated variable
A = 1/2(pi)(r)^2 solve for pi
Answers
Answer:
(2A)/(r^2)=pi
Step-by-step explanation:
The goal is to get pi by itself, so you have to move all the other elements over
2A=pir^2
(2A)/(r^2)=pi
find the value of k for which the vectors [−1−514] and [05−4k] are orthogonal.
Answers
Given the two vectors are orthogonal vectors. Then, the value of k is found to be \(k=-\frac{25}{56}\).
When the two vectors are perpendicular or right angle to each other and their dot product value is equal to zero, they are considered orthogonal vectors. Consider two vectors u and v. These two vectors are considered orthogonal when their inner product is zero. That is, \(u\cdot v=u_1v_1+u_2v_2+\cdots+u_nv_n=0.\)
They also have a magnitude of 1. So the three conditions required for the vectors to be orthogonal are:
\(u\cdot v=0\)\(\|{u}\|=0\)\(\|{v}\|=0\)Given the two vectors,
\(\mathbf{x}=\left[\begin{array}{ccc}-1\\-5\\14\end{array}\right]\)
\(\mathbf{y}=\left[\begin{array}{ccc}0\\5\\-4k\end{array}\right]\)
Then, their dot product is given as follows,
\(\begin{aligned}x\cdot y&=0\\(-1\times0)+(-5\times5)+(14\times-4k)&=0\\-25-56k&=0\\-56k&=25\\k&=\frac{-25}{56}\end{aligned}\)
The required answer is \(k=-\frac{25}{56}\).
To know more about orthogonal vectors:
https://brainly.com/question/28503609
#SPJ4
The complete question is -
Find the value of k for which the vectors \(\mathbf{x}=\left[\begin{array}{ccc}-1\\-5\\14\end{array}\right]\) and \(\mathbf{y}=\left[\begin{array}{ccc}0\\5\\-4k\end{array}\right]\) are orthogonal.
a pizza restaurant sells pizzas in three sizes, and a customer can choose up to three toppings, from a list of ten. a customer may not repeat toppings (e.g. they cannot order triple pepperoni, or pepperoni pepperoni sausage). how many pizza configurations are possible?
Answers
There are 360 possible pizza configurations possible.
To find the number of pizza configurations that a customer can choose, use the fundamental principle of counting where we multiply the number of choices for each category.
For the pizza size, there are 3 options to choose from.
For the toppings, there are 10 options for the first topping, 9 options for the second topping, and 8 options for the third topping.
However, since the order of the toppings doesn't matter (e.g. pepperoni, sausage, and mushroom is the same as mushroom, sausage, and pepperoni), we have to divide the result by the number of ways to arrange each group of toppings, which is 3! (factorial of 3).
So, the number of pizza configurations that a customer can choose can be calculated as follows:
Number of configurations = 3(10)(9)(8) / 3!
= 3(720) / 6
= 3(120)
= 360
Therefore, there are 360 possible pizza configurations that a customer can choose.
Learn more about fundamental principle of counting here: https://brainly.com/question/2063455
#SPJ4
Name the polygon. Then tell whether it is a regular polygon or not a regular polygon.

Answers
Answer:
not a regular polygon
Step-by-step explanation:
A regular polygon is an n-sided polygon in which the sides are all the same length and are symmetrically placed about a common center
While scanning through the dessert menu of your favorite restaurant, you notice that it lists 12 desserts that include yogurt, fruit, or both. Of these, 8 include yogurt, and 7 include fruit. How many of the desserts with yogurt also include fruit
Answers
There are 7 desserts that have both yogurt and fruit. Therefore, the answer to your question is 7.
To find out how many of the desserts with yogurt also include fruit, we need to use the concept of intersection in set theory. We can create two sets: one for desserts with yogurt and another for desserts with fruit.
The set of desserts with yogurt has 8 elements, and the set of desserts with fruit has 7 elements. We can represent these sets as follows:
Y = {yogurt desserts} = {1, 2, 3, 4, 5, 6, 7, 8}
F = {fruit desserts} = {1, 2, 3, 4, 5, 6, 7}
Now we need to find the intersection of these sets, i.e., the desserts that have both yogurt and fruit. To do this, we can count the number of elements in the set Y ∩ F:
Y ∩ F = {yogurt and fruit desserts} = {1, 2, 3, 4, 5, 6, 7}
So there are 7 desserts that have both yogurt and fruit. Therefore, the answer to your question is 7.
Visit here to learn more about intersection : https://brainly.com/question/14217061
#SPJ11
Michael is collecting sea glass from the beach. He begins with 14 pieces in his collection and adds 3 new pieces per day. How many days will it take Michael to have 80 pieces of sea glass in his collection?
Answers
Answer:
It would take Michael 22 days
Explanation:
The end goal is to have 80 and we begin with 14
So, 80 - 14 = 66 pieces left to collect
If he collects 3 per day we'll divide 66 by 3, which equals 22
Therefore it takes him 22 days!
(hope this helps :D )
Answer: 22 days
Step-by-step explanation: 22 x 3 = 66, 66 + 14 equals 80