Solve for A if
π = 3.14 and r = 3.
A = πr²
Answers
Answer:
28.26
Step-by-step explanation:
Formula: A = πr² OR A = π × r × r
π = 3.14 and r = 3.
We take these numbers and plug them into the formula.
A = π × r × r ⇒ A = 3.14 × 3 × 3
= 28.26
Related Questions
Isabelle went for a hike on Wednesday at camp. The hike took 2 hours and 10 minutes. As soon as she got back, Isabelle played volleyball for 1 hour and 55 minutes. It was 11:15 A.M. When Isabelle finished playing volleyball. What time did Isabelle start her hike?
Answers
Answer: 5:10 A.M.
Step-by-step explanation:
First find the total time that Isabelle spent playing volleyball and hiking.
= 2 hours and 10 minutes + 1 hour and 55 minutes
= 4 hours and 5 minutes
If she finished both activities at 11:15 am, the time she started was:
= 11:15 - 4 hours 5 minutes
= 5:10 A.M.
Additional Mathematics

Answers
Answer:
a = 1000, p = 10
Step-by-step explanation:
Given
y = - 3lg x + lg a
in the form y = mx + c ( m is the slope and c the y- intercept )
From the graph
(a)
c = 3 , then
lg a = 3 , that is
a = 10³ = 1000
(b)
Replace x by p and y = 0 in the equation
0 = - 3lg p + 3 ( subtract 3 from both sides )
- 3 = - 3lg p ( divide both sides by - 3 )
1 = lg p
p = 10 [ \(log_{10}\) 10 = 1 ]
76. 6 25. 5 10. 87 =
What wa Sela' etimate and what i the actual um of the number?
Answers
The estimate for the sum of the numbers is 230, and the actual sum of the numbers is 209.
To estimate the sum of the numbers, we can round each number to the nearest ten and then add them together. When rounding off to the nearest tens, we look at the number at the tenth position. If it is five and above, we round it off to the next nearest tens number and if it is below five, we round it off to the previous nearest tens number.
76 rounds to 80 since 6 is above 5
6 rounds to 10 since 6 is above 5
25 rounds to 30 since 5 is located at 5 and above interval
5 rounds to 10 since 5 is located at 5 and above interval
10 rounds to 10 since 0 is below 5
87 rounds to 90 since 7 is above 5
So, the estimate for the sum of the numbers is: 80 + 10 + 30 + 10 + 10 + 90 = 230
To find the actual sum of the numbers, we simply add them together without rounding:
76 + 6 + 25 + 5 + 10 + 87 = 209
The complete question is: 76. 6 25. 5 10. 87 =
What was Sela's estimate and what is the actual sum of the number?
More such examples on estimation of numbers can be found here: https://brainly.com/question/30545404
#SPJ11
Law of sines: startfraction sine (uppercase a) over a endfraction = startfraction sine (uppercase b) over b endfraction = startfraction sine (uppercase c) over c endfraction 2.2 units 2.4 units 3.0 units 3.3 units
Answers
The possible approximate lengths of b are: 2.3 units and 7.8 units
We know that the law of sines for triangle is:
The ratios of the length of all sides of a triangle to the sine of the respective opposite angles are in proportion.
This means, for triangle ABC,
\(\frac{sin~ A}{a} =\frac{sin~B}{b} =\frac{sin~ C}{c}\)
where a is the length of side BC,
b is the length of side AC,
c is the length of side AB.
For triangle ABC consider an equation from sine law,
\(\frac{sin~ A}{a} =\frac{sin~ C}{c}\)
here, c = 5.4, a = 3.3, and m∠A = 20°
\(\frac{sin~ 20}{3.3} =\frac{sin~ C}{5.4}\\\\\frac{0.3420}{3.3} =\frac{sin~ C}{5.4}\)
0.3420 × 5.4 = 3.3 × sin(C)
sin(C) = 0.5596
∠C = arcsin(0.5596)
∠C = 34.03° OR 145.9°
∠C ≈ 34° OR 146°
We know that the sum of all angles of triangle is 180 degrees.
so, ∠A + ∠B + ∠C = 180°
when m∠C = 34°,
20° + ∠B + 34.03° = 180°
∠B = 125.97°
m∠B = 126°
when m∠C = 146°,
20° + ∠B + 146° = 180°
m∠B = 14°
Now consider equation,
\(\frac{sin~ A}{a} =\frac{sin~ B}{b}\\\\\frac{sin~20^{\circ}}{3.3} =\frac{sin~ 126^{\circ}}{b}\)
b × 0.3420 = 0.8090 × 3.3
b = 7.8 units
when m∠B = 14°,
\(\frac{sin~20^{\circ}}{3.3} =\frac{sin~ 14^{\circ}}{b}\)
b × 0.3420 = 0.2419 × 3.3
b = 2.3 units
Learn more about the law of sines here:
https://brainly.com/question/17289163
#SPJ4
The complete question is:
Law of sines: StartFraction sine (uppercase A) Over a EndFraction = StartFraction sine (uppercase B) Over b EndFraction = StartFraction sine (uppercase C) Over c EndFraction
In ΔABC, c = 5.4, a = 3.3, and measure of angle A = 20 degrees. What are the possible approximate lengths of b? Use the law of sines to find the answer.
2.0 units and 4.6 units
2.1 units and 8.7 units
2.3 units and 7.8 units
2.6 units and 6.6 units
could u plz answer this
2x-7=13
3x+4=25
Answers
Answer:
x=10
Step-by-step explanation:
16. p(ski | does not snowboard)
a. 3/17 b.7/17 c.3/7 d. 3/13
- this is the part i need help with
Answers
The correct option is b) In order to determine the probability of skiing given that someone does not snowboard, we need to use conditional probability. We know that the probability of not snowboarding is 1 minus the probability of snowboarding, which is 1 - 7/17 = 10/17.
Now, we can use Bayes' theorem to find the probability of skiing given that someone does not snowboard:
P(ski | not snowboard) = P(not snowboard | ski) * P(ski) / P(not snowboard)
We don't have the probability of not snowboarding given that someone skis, so we have to assume that it's the same as the probability of not skiing given that someone snowboards, which is 3/7. We also know that the probability of skiing is 3/13. So, plugging these values into the formula:
P(ski | not snowboard) = (3/7) * (3/13) / (10/17) = 27/130
Therefore, the answer is not listed among the choices given.
To know more about Probability visit :
https://brainly.com/question/31828911
#SPJ11
Find x parallel angle measures
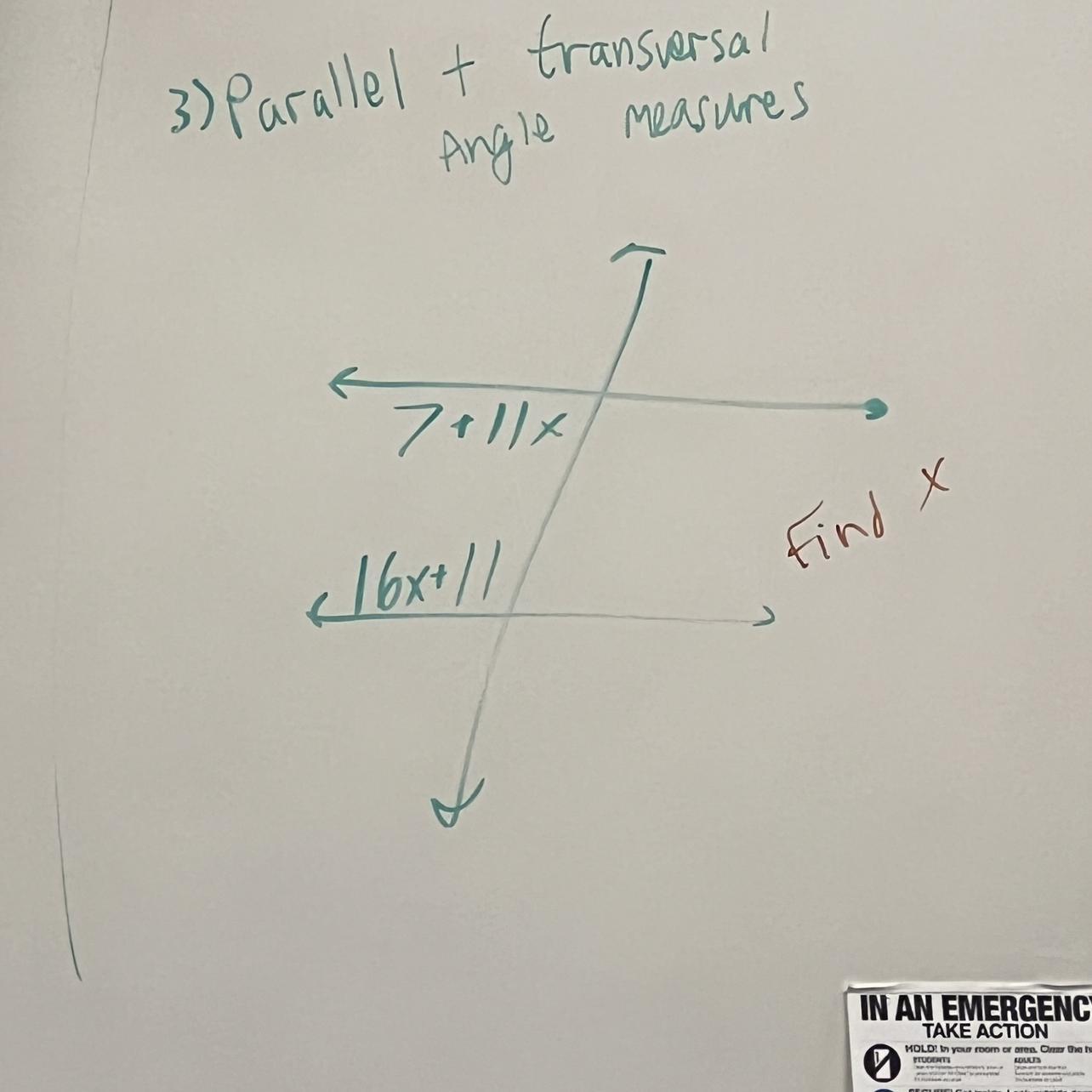
Answers
Answer:
6
Step-by-step explanation:
(7+11x)+(16x+11)=180⁰ (being co-interior angle)
or, (18+27x)=180⁰
or, 27x=180⁰-18
or, 27x=162⁰
or, x=162/27
or, x=6 Answer.
Kerry wants to give each student in her class 1/2 of a small pizza for lunch. There are 30 students in her class
Answers
Answer:
15
Step-by-step explanation:
she will need 15 pizzas because there is 30 students in her class and each will have 1/2 meaning there is 1 whole pizza per two students and 30 divided by 2 is 15
If f(1) = 7 and f(n) = -3f(n − 1) then find the value of f(6).
Answers
Answer:
-1701
Step-by-step explanation:
The recursion relation tells you each term of the sequence is -3 times the previous term. Then the first 6 terms are ...
7, -21, 63, -189, 567, -1701
The value of f(6) is -1701.
_____
Additional comment
The explicit formula for a geometric sequence with first term 7 and common ratio -3 is ...
f(n) = 7×(-3)^(n-1)
Then f(6) is ...
f(6) = 7×(-3)^5 = 7×(-243) = -1701
A math test has a total of 25 problems. Some problems are worth 2 points and some are worth 4 points. They add up to 60 points. How many problems worth 2 points and problems worth 4 points are there on the test?
Answers
Answer:
25.
Step-by-step explanation:
can someone help me please

Answers
Answer:
(4x + 5)(x² + 25)
Step-by-step explanation:
Given
4x³ + 5x² + 100x + 125 ( factor the first/second and third/fourth terms )
= x²(4x + 5) + 25(4x + 5) ← factor out (4x + 5) from each term
= (4x + 5)(x² + 25)
have yall answer fast please and thank you

Answers
what the answer for order of operations 50+50-25x0+2+2 ?
Answers
help pls im stuck thank u guys

Answers
Answer:
The answer is 36.
Step-by-step explanation:
*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^
First, divide 108 by 12.
The result is 9.
Now square root 9.
The result is 3.
Now, multiply 12 by 3.
The result is 36.
To check that this is the pattern, we multiply 36 by 3, and we indeed see that 3 times 36 is equal to 108.
*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^
#teamtrees #WAP (Water And Plant)
What happens if you try to use l' Hospital's Rule to find the limit? lim_x rightarrow infinity x/Squareroot x^2 + 3 You cannot apply l' Hospital's Rule because the function is not continuous. You cannot apply l'Hospital's Rule because the denominator equals zero for some value x = a. You cannot apply l'Hospital's Rule because the numerator equals zero for some value x = a You cannot apply l'Hospital's Rule because the function is not differentiable. Repeated applications of l'Hospital's Rule result in the original limit or the limit of the reciprocal of the function Evaluate the limit using another method.
Answers
The limit lim(x→∞) x/√(x^2 + 3) is 1, and there is no need to apply L'Hospital's Rule in this case.
When trying to use L'Hospital's Rule to find the limit lim(x→∞) x/√(x^2 + 3), it is important to note that L'Hospital's Rule can only be applied if the function is continuous and differentiable. In this case, the function is continuous and differentiable, but applying L'Hospital's Rule is not necessary as the limit can be evaluated using another method.
First, let's rewrite the given function by dividing both the numerator and the denominator by x:
lim(x→∞) (x/x) / (√(x^2 + 3)/x) = lim(x→∞) 1 / √(1 + 3/x^2)
As x approaches infinity, the term 3/x^2 approaches 0, so the limit becomes:
lim(x→∞) 1 / √(1 + 0) = 1 / √(1) = 1
Therefore, the limit lim(x→∞) x/√(x^2 + 3) is 1, and there is no need to apply L'Hospital's Rule in this case.
To know more about Limit visit:
https://brainly.com/question/12207539
#SPJ11
5/2 , 2.45, 2 2/5 , 6√ Put the numbers in order from least to greatest.
Answers
154b
Step-by-step explanation:
the tortoise and the hare are running a 1 km race. after running comfortably for 7 s, the hare is so far ahead that he decides to take a nap under a tree, 100 m away from the finish line. if the tortoise is moving constantly at a speed of 0.27 m/s, and the maximum speed of the hare is 15 m/s, how long can the hare afford to nap if he does not want to lose the race?
Answers
The hare can afford to nap for a maximum time of 3,690 seconds without losing the race if his speed is 15 m/s.
After running for 7 seconds, the hare has covered a distance of:
\(distance = speed \times time\\distance = 15 \times 7\\\)
distance = 105m
The hare is now 895 m away from the starting line and 100 m away from the finish line.
The hare needs to cover a distance of 100 m to reach the finish line, while the tortoise needs to cover a distance of 895 m.
calculate the time it would take the tortoise to reach the finish line:
\(time = \frac{100}{0.27}\) = 3704 seconds
The maximum speed of the hare is 15 m/s, which means the time it would take the hare to cover the distance is:
\(time = \frac{100}{15}\) = 6.67 seconds
so, the time hare have to nap so that he does not lose race = 3704 - (7+6.67) ≅3690 seconds
To know more about speed
https://brainly.com/question/30670429
#SPJ4
The boom of a sailboat is 26 feet long. If the sail is an equilateral triangle how much cloth will be required to make the sail of the boat?
Answers
The area or amount of cloth that will be required to make the sail of the boat is 50.5 square feet (approx.).
Given that the boom of a sailboat is 26 feet long and the sail is an equilateral triangle. We have to determine the amount of cloth that will be required to make the sail of the boat.
The formula to calculate the area of an equilateral triangle is:
A = (√(3)/4)*a²,
where
A represents the area of the equilateral triangle
a represents the side of the equilateral triangle.
Here, the sail is an equilateral triangle.
Therefore, the length of each side of the sailboat is given as:
Length of each side of the sailboat = 26 feet / 3
= 8.67 feet or 8 feet (approximately)
We can calculate the area of the sail using the below formula;
A = (√(3)/4)×a²,
where,
A represents the area of the equilateral triangle
a represents the length of each side of the sailboat.
By substituting the value of a = 8.67 in the above equation, we get the area of the sail as follows:
A = (√(3)/4)×a²
A = (√(3)/4)*(8.67)²
A = 50.5 square feet (approx.)
Hence, the amount of cloth that will be required to make the sail of the boat is 50.5 square feet (approx.).
To know more about equilateral triangle, visit:
https://brainly.com/question/32499398
#SPJ11
how do you find out 5 times 14 in distributiveprpoerty
Answers
Answer:70
Step-by-step explanation:
5(14)=5x14=70
The Steady Price Phone Company has a new calling plan that charges a flat fee plus a per minute fee as described by the equation below. Determine which table matches the equation: y = $0.25x + $35.95.

Answers
To determine which of the tables matches with the equation, we will need to substitute the X value and check which one is the one that matches with it.
Because for Minutes = 24 each SPPC Pricing Plan has a different cost, we will use it to determine easily which one is the correct.
By substituting 24 in the equation, we have the following:
\(\begin{gathered} y=0.25\cdot24+35.95 \\ y=6+35.95 \\ y=R\$41.95 \end{gathered}\)From the solution developed above, the only possible correct answer for the present question is the table C)
Two opposite angles of a parallelogram are 3x+4 and 5x-2 find measure of all angles of parallelogram
Answers
Answer:
=The opposite angles of a parallelogram are equal
=(3x+4)
=(5x-2)
=-2x=-6
=x=6+2
=x=3=
1st angle=3x+4=13
3rd angle=5x-2=13
=sum of adjacent side of angle is 180°
=Let the adjacent (2nd angle ) be y=
y+13°=180°
=y=180°-13°
=y=167°=
2nd angle=4th angle
=2nd angle=167°
=4th angle=167°
Step-by-step explanation:
This might be confusing, but I hope it helps <3
Fill in the next multiple of 6 and the next multiple of 10.
1. List the multiples of each number, starting with each number itself.
2. Keep listing multiples until a number common to both lists is found.
Multiples of 6: 6, 12, 18,
...
Multiples of 10: 10, 20, 30,
...
Answers
40
Step by step explanation This is how I got the answer to your question and I gave you the solution I hope this helps you out
A study on students drinking habits wants to determine the true average number of alcoholic drinks all uf greek students have in a one week period. We know from preliminary studies that the standard deviation is around 6. 3. How many students should be sampled to be within 0. 5 drink of population mean with 95% probability?.
Answers
Number of students need to be sampled = 610
A study to determine the true average number of alcoholic drinks consumed by Greek students is conducted.
Standard Deviation, σ = 6.3
Margin Error of population mean, E = 0.5
Probability = 95% = 0.95
The p-value corresponding to 0.95 probability = (1+0.95)/2 = 0.975
The z-score corresponding to this p-value = 1.96 [from the z-tables]
Now, The margin error, E = zσ/√n, where n is the sample size
⇒ n = (zσ/E)²
⇒ n = (1.96 x 6.3/0.5)²
⇒ n ≈ 610
Hence 610 students need to be sampled.
Learn more about z-score at https://brainly.com/question/25638875
#SPJ4
find the remainder in the taylor series centered at the point a for the following function. then show that limn→[infinity]rn(x)=0 for all x in the interval of convergence. f(x)=e−x, a=0
First find a formula for f^n(x). f^n(x) = (Type an exact answer.) Next, write the formula for the remainder. R_n(x) = /(n 1)!^n 1, for some value c between x and 0 (Type exact answers.) Find a bound for |R_n(x)| that does not depend on c, and thus holds for all n, Choose the correct answer below. A. |R_n(x)| greaterthanorequalto 1/(n 1)!(x-theta)^n 1 B. |R_n(x) lessthanorequalto e|x|/(n 1)! |x|^n 1 C. |R_n(X)| lessthanorequalto 1/(n 1)! (x-e)^n 1 D. |R_n(X)| lessthanorequalto e^x/(n 1)! x^n 1 E. |R_n(X)| greaterthanorequalto e^|x|/(n 1)! |x|^n 1 F. |R_n(x) greaterthanorequalto e^-x/(N 1)!|x-e|
Answers
To find the remainder in the Taylor series centered at a=0 for f(x)=e^(-x), we start by finding the nth derivative of f(x). Differentiating f(x) repeatedly, we observe that f^n(x) = (-1)^n * e^(-x).
The formula for the remainder in the Taylor series is given by R_n(x) = (f^(n+1)(c) * (x-a)^(n+1))/(n+1)!, where c is some value between x and a.
For our function, f^(n+1)(x) = (-1)^(n+1) * e^(-x), so the remainder becomes R_n(x) = (-1)^(n+1) * e^(-c) * (x-0)^(n+1)/(n+1)!
To find a bound for |R_n(x)| that does not depend on c, we can use the fact that e^(-c) is always less than or equal to 1. Therefore, we have |R_n(x)| ≤ (x)^(n+1)/(n+1)!.
Based on this, the correct answer is A. |R_n(x)| ≥ 1/(n+1)!(x-θ)^(n+1), where θ is some value between x and 0.
Learn more about Taylor series here: brainly.com/question/32067845
#SPJ11
Eight less than three times a number is -23
Answers
Answer: 10 is your answer bud ❤
notre prof de math vient de nous envoyer se travaille pour lundi je ne comprends rien sil vous plait aider moiii
Answers
Answer: f(2)=-10 f(-3)=15
Step-by-step explanation:
Let the number conceived be x.
Hence,
f(x)=(x+5)(-3)-2x+15
f(x)=-3x-15-2x+15
f(x)=-5x
Thus,
f(2)=(-5)(2)
f(2)=-10
f(-3)=(-5)*(-3)
f(-3)=15
Below are the jersey numbers of 11 players randomly selected from a football team. Find the range, variance, and standard deviation for the given sample data. What do the results tell us? 40 39 8 82 25 53 97 1 28 41 94
Answers
Answer:
(a)Range = 96
(b)Variance=1059.36
(c)Standard Deviation =32.55
Step-by-step explanation:
(a)Range
Highest Value = 97Lowest Value = 1Range = Highest Value - Lowest Value
=97-1
=96
(b)Variance
The variance of a sample for ungrouped data is defined by the formula:
\(Variance, s^2 = \dfrac{\sum(x-\overline{x})^2}{n-1}\)
First, we determine the mean of the sample data.
\(Mean = \dfrac{40 +39+ 8+ 82+ 25+ 53+ 97+ 1+ 28+ 41+ 94}{11} \\=\dfrac{508}{11}\\\\ \overline{x}=46.2\)
\(\sum(x-\overline{x})^2=(40-46.2)^2 +(39-46.2)^2+ (8-46.2)^2+ (82-46.2)^2+ (25-46.2)^2+ (53-46.2)^2+ (97-46.2)^2+ (1-46.2)^2+ (28-46.2)^2+ (41-46.2)^2+ (94-46.2)^2\\\\=38.44+51.84+1459.24+1281.64+449.44+46.24+2580.64+2043.04+331.24+27.04+2284.84\)
=10593.64
Therefore:
Variance, Variance,
\(Variance, s^2 = \dfrac{10593.64}{11-1}\\\\=1059.36\)
(c)Standard Deviation
\(s=\sqrt{Variance}\\ =\sqrt{1059.36}\\s=32.55\)
The results tell us that there is great variability in the number of jerseys of the player as evidenced by the high standard deviation and range.
Use the One-to-One Property to solve the equation for x. (Enter your answers as a comma-separated list.) log5(x+1)=log5(9) x=
Answers
The correct answer to the equation log5(x+1) = log5(9) is x = 8.
To solve the equation using the One-to-One Property of logarithms, we can equate the arguments of the logarithms: x + 1 = 9
Now, we can solve for x:
x = 9 - 1
x = 8 Therefore, the solution to the equation log5(x+1) = log5(9) is x = 8.
Let's go through the steps in more detail.
The equation we have is log5(x+1) = log5(9).
According to the One-to-One Property of logarithms, if two logarithms with the same base are equal, then their arguments must be equal as well.
In this case, since the base is 5, we can write:
x + 1 = 9
To solve for x, we isolate it on one side of the equation:
x = 9 - 1
x = 8
Therefore, the solution to the equation log5(x+1) = log5(9) is x = 8.
In summary, by using the One-to-One Property, we equated the arguments of the logarithms and solved for x to find the value that satisfies the equation.
Learn more about logarithms here:
https://brainly.com/question/30193034
#SPJ11
Find the area of the sector of the circle with radius r and central angle 0 R= 4 in 0= 3.14/4
Answers
The area of the sector of the circle is 12.56 in.²
How to Find the Area of a Sector of a Circle?Area of a sector of a circle = (θ/2) × r², given that:
r = radius of the circle
∅ = central angle of the sector in radians
Given the following:
Central angle of the sector (∅) = 3.14/4 =
Radius of the circle (r) = 4 in.
π = 3.14
Plug in the values into Area of a sector of a circle:
Area of a sector of a circle = 3.14/4 × 4²
Area of a sector of a circle = 3.14/4 × 16
Area of a sector of a circle = 3.14 × 4
Area of a sector of a circle = 12.56 in.²
Learn more about the area of a sector in:
https://brainly.com/question/22972014
#SPJ1
4/7
of a number is 36
What is the number?
Answers
\(\text{If the number is x,}\\\\~~~~~\dfrac 47 \cdot x =36\\\\\implies 4x = 36 \times 7\\\\\implies x =\dfrac{36 \times 7}4\\ \\\implies x = 9 \times 7\\\\\implies x = 63\\\\\text{Hence, the number is 63.}\)
Answer:
\(\huge\boxed{\bf\:x = 63}\)
Step-by-step explanation:
Given,
4/7th of a number = 36Let's take the unknown number as 'x'.
Now,
4/7 × x = 36
Take the reciprocal of 4/7 to the other side of the equation .
x = 36 × 7/4
Cancel 36 by 4.
x = 9 × 7
Multiply the 2 numbers
x = 63
\(\rule{150pt}{2pt}\)