Solve for x: 5x+2(3x+7)=3(x-6)
Answers
Answer:x=−2
Step-by-step explanation:
Related Questions
Suppose a population contains 20,000 people. All else being equal, a study
based on a population sample that includes which of the following numbers
of respondents would be the most reliable?
A. 200
OB. 20
C. 2000
D. 2
Answers
A study based on a population sample that includes 2000 respondents would be the most reliable out of the given options.
In statistical analysis, the reliability of a study depends on the representativeness and size of the sample.
A larger sample size generally provides more reliable results as it reduces the sampling error and increases the precision of the estimates.
Given that the population contains 20,000 people, we need to consider which number of respondents would yield the most reliable study.
Option A: 200 respondents
This represents only 1% of the population.
While it is better than having just 2 respondents, it may not be sufficient to accurately capture the characteristics of the entire population.
Option B: 20 respondents
This represents only 0.1% of the population.
With such a small sample size, the study would likely suffer from a high sampling error and may not provide reliable results.
Option C: 2000 respondents
This represents 10% of the population.
While it is a larger sample size compared to the previous options, it still only captures a fraction of the population.
The study may provide reasonably reliable results, but there is room for potential sampling error.
Option D: 2 respondents
This represents an extremely small sample size, accounting for only 0.01% of the population.
With such a small sample, the study would be highly susceptible to sampling bias and would likely yield unreliable results.
Based on the options provided, option C with 2000 respondents would be the most reliable study.
Although it does not include the entire population, a sample size of 2000 respondents provides a larger representation of the population and reduces the potential for sampling error.
However, it's important to note that the reliability of a study depends not only on sample size but also on the sampling method, data collection techniques, and other factors that ensure representativeness.
For similar question on population sample.
https://brainly.com/question/27859177
#SPJ8
Can you help me in this question?
(Also please write me how to solve it and ill check the answer if it is true then i will make you the brainliest.)

Answers
Answer:
C
Step-by-step explanation:
2m + 3m = 5m
9m - 5m = 4m
11m - 6m = 5m
Therefore, the expression 11m - 6m is equivalent to 2m + 3m
(as they both equal 5m)
Answer:
C. The expression 11m - 6m is equivalent to 2m + 3m.
Step-by-step explanation:
9m - 5m = 4m
11m - 6m = 5m
2m + 3m = 5m
verify sin2θ/1+cos2θ =tanθ

Answers
Answer:
LHS.= Sin 2x /( 1 + cos2x )
We have , sin 2x = 2 sinx•cosx
And. cos2x = 2cos^2 x - 1
i.e . 1+ cosx 2x = 2cos^2x
Putting the above results in the LHSwe get,
Sin2x/ ( 1+ cos2x ) =2 sinx•cosx/2cos^2x
=sinx / cosx
= Tanx
.•. sin2x/(1 + cos2x)= tanx
Step-by-step explanation:
Anne owns an art supply store. Anne is analyzing the store's expenses and income because she wants to increase the store's profits. The expenses include renting 1,250 square feet of space for $13,750 per month. The store has only one employee, who is paid $8.00 per hour plus 8% commission. Much of the
store's income comes from the sales of blank painting canvases and frames. The table shows the prices of the canvases and frames sold at the store.
Answers
$590
Correct me if I’m wrong
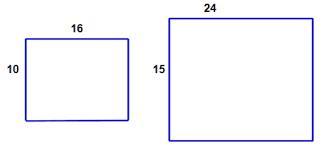
Jason says that all rectangles are similar because any two rectangles he chooses have 4 pairs of congruent corresponding angles. Gabby says Jason is wrong. Who is correct? Explain your answer.
Answers
Jason is right while Gabby is wrong because, two congruent rectangles are similar, but two similar rectangles may not be congruent.
For two figures to be considered similar, the following criterion must be satisfied:
All corresponding angles must be congruent.This means the only criterion necessary for two figures to be considered congruent is that they must have the same shape but not necessary the same size. i.e. equal corresponding angles and the same ratio of corresponding lengths.
On the other hand, for two figures to be considered congruent, the following must be satisficed:
Have equal corresponding side lengthsHave equal corresponding anglesThis implies that they must have the same shape and size.
Thus, if two rectangles have the 4 pairs of corresponding angles that are congruent, they are said to be similar.
The diagram of two similar rectangles is shown in the image attached below.
Therefore, Jason is right: all rectangles are similar.
Learn more about rectangles here:
https://brainly.com/question/20859443
a water snake in a well is 30 M below the ground level its lights 20 m upward and then slips down 10 M how far it is from the ground level
\( - 30 - + 20 - - 10\)
Answers
If the water snake is initially 30 meters below the ground level and then climbs 20 meters upward, it will be 30 - 20 = 10 meters below the ground level. However, if it then slips down 10 meters, it will be 10 + 10 = 20 meters below the ground level.
whats the answer for 3(h-5g) while using distributive property
Answers
Answer:
3h - 15g
Step-by-step explanation:
All you have to do is multiply 3 by h, and 3 by 5g, but you have to keep the subtraction, so it would be 3h - 15g
I really need help quickly please!!!!

Answers
Answer:The third one is!!
Step-by-step explanation:
The commutative property of addition says that changing the order of addends does not change the sum. Here's an example: 4 + 2 = 2 + 4 4 + 2 = 2 + 4 4+2=2+4
Write and solve an inequality to find the possible values of x.

Answers
The inequality tha calculates the possible values of x is x < 2
How to determine the inequality tha calculates xFrom the question, we have the following parameters that can be used in our computation:
The figure
Where, we have
3x + 2 < 10
And, we have
2x + 6 < 10
Evaluate the expressions
So, we have
3x < 8 and 2x < 4
Evaluate
x < 8/3 and x < 2
Hence, the inequality tha calculates x is x < 2
Read more about inequality at
https://brainly.com/question/32124899
#SPJ1
Calculate: ㅤ \(\lim_{x \rightarrow +\infty}x(\sqrt{x^{2}-1}-x)\)
Answers
Answer:
\(\displaystyle \large \boxed{ \lim_{x \rightarrow +\infty} {x\left(\sqrt{x^2-1}-x\right)}=-\dfrac{1}{2}}\)
Step-by-step explanation:
Hello, please consider the following.
\(\sqrt{(x^2-1)}-x\\\\=\sqrt{x^2(1-\dfrac{1}{x^2})}-x\\\\=x\left( \sqrt{1-\frac{1}{x^2}}-1\right)\)
For x close to 0, we can write
\(\sqrt{1+x}=1+\dfrac{1}{2}x-\dfrac{1}{8}x^2+o(x^2)\\\\\ \text{x tends to } +\infty \text{ means }\dfrac{1}{x} \text{ tends to 0}\\\\\text{So, when }\dfrac{1}{x}\text{ is close to 0, we can write.}\\\\\sqrt{1-\dfrac{1}{x^2}}=1-\dfrac{1}{2}\dfrac{1}{x^2}-\dfrac{1}{8}\dfrac{1}{x^4}+o(\dfrac{1}{x^4})\)
So,
\(x\left( \sqrt{1-\frac{1}{x^2}}-1\right)\\\\=x(1-\dfrac{1}{2}\dfrac{1}{x^2}+o(\dfrac{1}{x^2})-1)\\\\=-\dfrac{1}{2x}+o(\dfrac{1}{x})\)
It means that
\(\displaystyle \lim_{x \rightarrow +\infty} {x\left(\sqrt{x^2-1}-x\right)}\\\\=\lim_{x \rightarrow +\infty} {-\dfrac{x}{2x}}=-\dfrac{1}{2}\)
Thank you
A man gave 90000.00 to his two daughters Jane and Lydia, 75.00 was given to Lydia to pay her load. After sharing the money Lydia has twice as
much as Jane. How much did each received?
Answers
Jane received $30025 and Lydia received $60000. Let's assume the amount of money that Jane received as x; then Lydia's share of the money will be twice the share of Jane.
We are to find out the share of each person. Here is the solution in steps:Suppose Jane's share was x dollars, and Lydia's share was y dollars.
Given that the total amount given to the two daughters was $90000. Also, given that Lydia paid off her $75, hence she got $75 less than Jane.
Therefore, y = 2x - 75; this is because we are given that Lydia got twice the share of Jane, and also, she got $75 less than Jane. Hence, x + y = $90000, this is because the total sum of money shared is $90000.
Substituting y = 2x - 75 into x + y = $90000 gives x + (2x - 75) = $90000.
Simplifying, we have :3x = $90000 + 75 = $90075.
Dividing both sides by 3, we get:x = $30025. Hence, Jane's share is $30025 Lydia's share = 2x - 75 = 2($30025) - $75 = $60075 - $75 = $60000.
Therefore, Jane received $30025 and Lydia received $60000.
For more question on amount
https://brainly.com/question/25720319
#SPJ8
Here is the problem I need help with

Answers
Answer:
8.302
Step-by-step explanation:
cos(41)x/11
since x is on top then just multiply
cos(41)(11)
x=8.302 round it how u like
Answer:
8.3
Step-by-step explanation:
It has been awhile since I have done this so I may be a bit rusty.
a = (sin(A)⋅b) / sin(B) = (sin(49.00∘)⋅11.00) / (sin(90.00∘)) = 8.30
Complete the equation that can be used to find the final sale price of an item after a 6% markup if the original price was C and the final
price is f.
HELP PlSS
Answers
Answer:
Step-by-step explanation:
You paid C dollars for an item that you sold at a 6% profit.
F = 1.06C
4. What is the y-intercept of this equation?
y=7X-6
Answers
Answer:
-6
Step-by-step explanation:
\(y = 7x - 6 \\ \\ equating \: it \: with \\ \\ y = mx + b \\ \\ b = - 6 \\ y - intercept = - 6\)
Prove: Quadrilateral EFGH is a trapezoid but not an isosceles trapezoid

Answers
It is true that the quadrilateral EFGH is a trapezoid but not an isosceles trapezoid
The coordinates are given as:
E = (-3,-5)F = (-2,0)G = (2,3)H = (5,1)How to prove that EFGH is not an trapezoidStart by calculating the slopes of the parallel sides (i.e. sides FG and EH) using the following slope formula
\(m = \frac{y_2 -y_1}{x_2 -x_1}\)
So, we have:
\(m_{FG} = \frac{3-0}{2 +2}\)
\(m_{FG} = \frac{3}{4}\)
\(m_{EH} = \frac{1 +5}{5 +3}\)
\(m_{EH} = \frac{6}{8}\)
Reduce the fraction
\(m_{EH} = \frac{3}{4}\)
By comparison, the slopes of the parallel sides are equal (i.e 3/4)
Next, calculate the side lengths of the slant sides (i.e. EF and GH) using the following distance formula
\(d = \sqrt{(x_2 -x_1)^2 + (y_2 - y_1)^2}\)
So, we have:
\(d_{EF} = \sqrt{(-2 +3)^2+ (0+5)^2 }\)
\(d_{EF} = \sqrt{26}\)
\(d_{GH} = \sqrt{(5 -2)^2 + (1 - 3)^2}\)
\(d_{GH} = \sqrt{13}\)
By comparison, the side lengths of the slant sides are not equal
Because the slant sides do not have congruent side lengths, and the slopes of the parallel sides are equal; then the quadrilateral EFGH is a trapezoid but not an isosceles trapezoid
Read more about isosceles trapezoids at:
https://brainly.com/question/4758162
4. Both the Galapagos Islands and the island of Naura are on the Equator, but the Galapagos Islands are at 90.30◦W whereas the island of
Nauru is at 166.56◦E. How far is it from the Galapagos Islands to
Nauru traveling over the Pacific ocean along the Equator, correct to
the nearest km ?
Answers
Answer:
Distance between Nauru and Galapagos islands = 11525 Km to the nearest Km
Step-by-step explanation:
The angle between the two Islands is given as X
X = (180 - 166.56) + (180 - 90.30)
X = 13.44° + 89.70°
X = 103.14
Distance between the islands = length of the arc with angle X subtended at the center of the earth of radius R.
Length of arc = (X/360) × 2πR
Where, R, radius of the earth = 6400 Km
Length of arc = (103.14/360) × 2π × 6400 Km
Length of arc = 11525.48 Km
Therefore, distance between Nauru and Galapagos islands = 11525 Km to the nearest Km
Ed bought some
t-shirts at a yard sale.
He gave 3 to his sister
and had 6 left. How
many t-shirts did Ed
buy at the yard sale?
Answers
Answer:
9. he bought 9.
Sphenathi and other matriculants plan to pass Bloemfontein at 07.25 to travel the above stated distance to Uptington. Determine (to the nearest km/h) the average speed at which they must travel to be in Uptington by 09:45.
Answers
Sphenathi and the other matriculants must travel at an average speed of approximately 107 km/h to reach Uptington by 09:45.
To determine the average speed at which Sphenathi and the other matriculants must travel to reach Uptington by 09:45, we need to calculate the time available for the journey and the distance between the two locations.
The time available is from 07:25 to 09:45, which is a total of 2 hours and 20 minutes. We need to convert this time to hours by dividing by 60:
2 hours + 20 minutes / 60 = 2.33 hours
Now, let's calculate the distance between Bloemfontein and Uptington. Suppose the distance is 'd' kilometers.
We can use the formula for average speed: average speed = distance / time
In this case, the average speed should be such that the distance divided by the time is equal to the average speed.
d / 2.33 = average speed
Now, let's assume that Sphenathi and the other matriculants must travel a distance of 250 kilometers to reach Uptington. We'll substitute this value into the equation:
250 / 2.33 = average speed
To find the average speed to the nearest km/h, we'll calculate the result:
average speed ≈ 107.3 km/h
Therefore, Sphenathi and the other matriculants must travel at an average speed of approximately 107 km/h to reach Uptington by 09:45.
For more questions on average speed
https://brainly.com/question/553636
#SPJ8
• The volume of a cube is 17 cubic inches. What expression represents the length of one side of the cube?
(remember the cube problem from the review yesterday!)
If the volume of a cube is an integer value of cubic inches, when will the length of one side of the cube be
irrational?
Answers
Step-by-step explanation:
The volume of a cube is 17 cubic inches.
The formula used to find the volume of a cube is given by :
\(V=x^3\)
x is the side of the cube
\(x=(V)^{1/3}\\\\x=(17)^{1/3}\\\\x=2.57\ \text{inches}\)
The fraction that cannot be written in the form of p/q is irrational no. If the cube root a number is not possible, then the length is considered to be irrational.
Solve the equation below. If the solution is not an integer, give it in fractional form reduced to lowest terms.
X-9 over 4 =3
Answers
Answer:
x = 21
eliminate the denominator of 4
you can do this buy multiplying both sides by 4
x -9 = 12
x = 21
solve z^3=27 it's a complex number
Answers
Answer:
z³=27
³√z³=³√27
z=3
Step-by-step explanation:
z³=27
³√z³=³√27
z=3
Answer:
the answer is 3
if you want the answer with complex number the Answer will be (-3i⁶)
because (-3)³ equal -27
and (i⁶)³ its i¹⁸ and the same time its i² so its -1
A three digit number is formed at random using the digits
2, 3 and 4. If no digit can be repeated in any one number, find the probability that the number formed is greater than 300.
Answers
Answer:
2/3, or 66.7%
Step-by-step explanation:
There are 2 options for the first digit (3 or 4).
After the first digit is selected, it cannot be repeated, so there are 2 options left for the second digit.
After the first two digits are selected, there is only 1 option for the third digit.
So there are 4 permutations greater than 300.
The total number of permutations is 3! = 6.
So the probability is 4/6 = 2/3.
Question 9
Use algebra to show that 4.57 (5 and 7 recurring) equal 4 and 19/33
Answers
o show that 4.57 (5 and 7 recurring) is equal to 4 and 19/33, we can use algebraic equations. First, let x = 4.57 (5 and 7 recurring), then we multiply both sides by 100 to get 100x = 457.5757... Next, we subtract x from 100x to get 99x = 453. Thus, x = 453/99. We can simplify this fraction by dividing both the numerator and denominator by 3, giving us 151/33. Finally, we can write 151/33 as a mixed number, which is 4 and 19/33. Therefore, we have shown that 4.57 (5 and 7 recurring) is equal to 4 and 19/33 using algebraic equations.
please help I'll give brilliantist:)

Answers
Answer:
-7
Step-by-step explanation:
The full coordinate is (-7,3) the dot is on the line between -6 and -8
Answer:
-7
Step-by-step explanation:
x = 3
y = -7
the answer is just -7
Suppose a random variable, x, follows a Poisson distribution. Let μ = 2.5 every minute, find the P(X ≥ 125) over an hour. Round answer to 4 decimal places.
Answers
Answer:
P(X ≥ 125) = 0.9812
Step-by-step explanation:
To solve this question, we need to understand the Poisson distribution and the normal distribution.
Poisson distribution:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:
\(P(X = x) = \frac{e^{-\lambda}*\lambda^{x}}{(x)!}\)
In which
x is the number of sucesses
e = 2.71828 is the Euler number
\(\lambda\) is the mean in the given interval, which is the same as the variance.
Normal distribution:
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
The Poisson can be approximated to the normal, with \(\mu = \lambda, \sigma = \sqrt{\lambda}\)
Let μ = 2.5 every minute
This is the mean of the Poisson, so \(\lambda = 2.5n\), in which n is the number of minutes.
P(X ≥ 125) over an hour
An hour has 60 minutes, so \(n = 60, \lambda = 2.5*60 = 150, \sigma = \sqrt{150} = 12.25\)
Using continuity correction, this is \(P(X \geq 125 - 0.5) = P(X \geq 124.5)\), which is 1 subtracted by the pvalue of Z when X = 124.5. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{124.5 - 150}{12.25}\)
\(Z = -2.08\)
\(Z = -2.08\) has a pvalue of 0.0188
1 - 0.0188 = 0.9812
So
P(X ≥ 125) = 0.9812
Find the solution of the system for which

Answers
Answer:
3,0,-6,0
Step-by-step explanation:
x1=3 because 3+0+0=3
since x2 and s2=0.
Solve (x+1)2 =13/4 using the square root property
Answers
Answer:
Starting with the equation:
(x + 1)^2 = 13/4
We can use the square root property, which states that if a^2 = b, then a is equal to the positive or negative square root of b.
Taking the square root of both sides, we get:
x + 1 = ±√(13/4)
Simplifying under the radical:
x + 1 = ±(√13)/2
Now we can solve for x by subtracting 1 from both sides:
x = -1 ± (√13)/2
Therefore, the solutions to the equation are:
x = -1 + (√13)/2 or x = -1 - (√13)/2
Step-by-step explanation:
Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers.
Write with fractional exponents. (Do not use parentheses.)

Answers
Answer:
4\(y^{\frac{3}{2} }\)
Step-by-step explanation:
using the rule of exponents/ radicals
\(\sqrt[n]{a^{m} }\) = \(a^{\frac{m}{n} }\)
then
4 \(\sqrt{y^{3} }\)
= 4\(y^{\frac{3}{2} }\)
convert the following to decimal fractions 99 by 5
Answers
Answer:
divide 99 by 5
99/5= 19.8
Bryan invests $6500 in two different accounts. The first account paid 11 %, the second account paid 7 % in interest. At the end of the first year he had earned $519 in interest. How much was in each account?
$ at 11 %
$ at 7 %
Answers
Bryan invested $1600 in the first account (earning 11% interest) and $4900 (6500 - 1600) in the second account (earning 7% interest).
Let's assume that Bryan invested an amount of x dollars in the first account, which earns 11% interest, and (6500 - x) dollars in the second account, which earns 7% interest.
The interest earned from the first account can be calculated as 0.11x, and the interest earned from the second account can be calculated as 0.07(6500 - x).
According to the problem, the total interest earned after one year is $519. So we can set up the equation:
0.11x + 0.07(6500 - x) = 519
Simplifying the equation:
0.11x + 455 - 0.07x = 519
0.04x + 455 = 519
0.04x = 64
x = 64 / 0.04
x = 1600
Therefore, Bryan invested $1600 in the first account (earning 11% interest) and $4900 (6500 - 1600) in the second account (earning 7% interest).
for such more question on Bryan invested
https://brainly.com/question/20690803
#SPJ8