Solve system of equations given below using both inverse matrix (if possible) and reduced row echelon forms. (20 Points each) a) xy + 2x2 + 2x3 = 1 X1 - 2x2 + 2x3 = -3 3x1 - x2 + 5x3 = 7 - b) x1 + 2xy + 2x3 + 5x4 = 0 *1 - 2x2 + 2x2 - 4x4 = 0 3x1 - x2 + 5x3 + 2x4 = 0 3x, -2x2 + 6x3 - 3x4 = 0.
Answers
The solution to the system of equations is x1 = -(9/7)x4, x2 = (2/7)x4, x3 = -(1/7)x4, and x4 is a free variable.
a) xy + 2x2 + 2x3 = 1 X1 - 2x2 + 2x3 = -3 3x1 - x2 + 5x3 = 7
We can solve the system of equations using both inverse matrix (if possible) and reduced row echelon forms.
We begin by converting the above equations into matrix form as follows:
[xy+2x2+2x3=1] [X1-2x2+2x3=-3] [3x1-x2+5x3=7] = [1] [-3] [7]
We represent the coefficient matrix by A and the variable matrix by X.
Then we have AX = B where B = [1] [-3] [7]
To find the inverse of A.
If the inverse of A exists, we can use it to find X = A^(-1)B.
We can find the inverse of A using the formula A^(-1) = adj(A)/|A| where adj(A) is the adjugate of A and |A| is the determinant of A.
We have: det(A) = |[1,2,2;-1,-2,2;3,-1,5]| = 9adj(A) = [11,6,-4;19,9,-5;-7,-4,3]
Therefore, A^(-1) = adj(A)/|A| = [11/9,2/3,-4/9;19/9,1/3,-5/9;-7/9,-4/3,1/9]
We can use A^(-1) to find X as follows:
X = A^(-1)B = [11/9,2/3,-4/9;19/9,1/3,-5/9;-7/9,-4/3,1/9][1;-3;7] = [-5/3;1/3;2/3]
Therefore, the solution to the system of equations is x = -5/3, y = 1/3, z = 2/3.
We can also solve the system of equations using the reduced row echelon form of the augmented matrix as follows:[1,2,2,1;-1,-2,2,-3;3,-1,5,7] [R2+R1,R3-3R1] [1,2,2,1;-4,-3,4,-2;0,-7,-1,4] [R2/(-4),R3/(-7)] [1,2,2,1;1/4,1,-1,1/2;0,1,1/7,-4/7] [R1-2R2, R3-(1/7)R2] [1,0,3/2,-1/2;0,1,1/7,-4/7;0,0,0,0]
The last row of the above matrix represents the equation 0x1 + 0x2 + 0x3 + 0x4 = 0, which is an identity.
The system of equations is consistent, and we can solve for x, y, and z using the first two rows of the above matrix as follows:
x + (3/2)z = (-1/2)y + (1/7)z = (4/7)
Solving for z, we have: z = 2/3
Substituting z into the first equation, we have:
x + (3/2)(2/3) = (-1/2)x = -5/3
Substituting z into the second equation, we have:
y + (1/7)(2/3) = (4/7)y = 1/3
Therefore, the solution to the system of equations is x = -5/3, y = 1/3, z = 2/3.b) x1 + 2xy + 2x3 + 5x4 = 0 *1 - 2x2 + 2x2 - 4x4 = 0 3x1 - x2 + 5x3 + 2x4 = 0 3x, -2x2 + 6x3 - 3x4 = 0
To solve this system of equations, we begin by converting it into matrix form as follows:[1,2y,2,5;0,-2,2,-4;3,-1,5,2;3,-2,6,-3] [x1;x2;x3;x4] = [0;0;0;0]
We represent the coefficient matrix by A and the variable matrix by X.
Then we have AX = 0. Our task is to find the reduced row echelon form of the augmented matrix [A|0].
We perform the following elementary row operations to the above matrix to obtain the reduced row echelon form:[1,2y,2,5,0;0,-2,2,-4,0;3,-1,5,2,0;3,-2,6,-3,0] [R1-2yR2, R3-3R2, R4-3R2] [1,0,-2y-1,2y+5,0;0,-2,2,-4,0;0,-7,-1,14,0;0,-8,0,9,0] [R3/(-7), R4/(-8)] [1,0,-2y-1,2y+5,0;0,-2,2,-4,0;0,1,1/7,-2/7,0;0,1,0,-9/8,0] [R1+(2y+1)R3] [1,0,0,9/7,0;0,-2,0,-2/7,0;0,1,1/7,-2/7,0;0,0,0,0,0]
The last row of the above matrix represents the equation 0x1 + 0x2 + 0x3 + 0x4 = 0, which is an identity.
The system of equations is consistent, and we can solve for x1, x2, x3, and x4 using the first three rows of the above matrix as follows:
x1 = -(9/7)x4x2 = (2/7)x4x3 = -(1/7)x4
Therefore, the solution to the system of equations is x1 = -(9/7)x4, x2 = (2/7)x4, x3 = -(1/7)x4, and x4 is a free variable.
To learn more about matrix
https://brainly.com/question/28180105
#SPJ11
Related Questions
4. For what values of p and q is ABCD a parallelogram?
Answers
The values of p and q that will make quadrilateral ABCD a parallelogram are: p = 1; q = 2.
What is the Value of p and q that Makes the Figure a Parallelogram?Recall that the diagonals of a parallelogram bisect each other to form congruent segments. Therefore, if the image in the attachment is a parallelogram, then the segments formed by the diagonals must be equal to each other.
Therefore, we have:
7p + 1 = 5p + 3
Combine like terms:
7p - 5p = -1 + 3
2p = 2
p = 1
3q + 1 = 2q + 3
Combine like terms:
3q - 2q = -1 + 3
q = 2.
Learn more about parallelogram on:
https://brainly.com/question/4314341
#SPJ1
7x - 3x + 2 = 8x - 6
Answers
Answer:
x=2
Step-by-step explanation:
What polygon is shown?

Answers
Answer:
Pentagon
Step-by-step explanation:
Madison has $6.50. Potatoes are $0.50 per pound. How many pounds of potatoes can Madison afford to buy?
In two or more complete sentences write and solve an inequality for this situation. Explain how you would solve this inequality.
Answers
Answer:
Part A:
You are given the amount of money Madison can spend and the price per pound for the potatoes. To find how many pounds Madison can buy, you would need to divide the amount of money she has by the price per pound.
The equation would be Pounds of potatoes = 6.50 / 0.50
Part B:
The only step required to solve the equation from part A is division.
Dividing 6.50 by 0.50 = 13. This means Madison can buy 13 pounds of potatoes.
To produce x units of a religious medal costs C(x) = 11x + 36. The revenue is R(x) = 23x. Both cost and revenue are in dollars. a. Find the break-even quantity. b. Find the profit from 470 units. c. Find the number of units that must be produced for a profit of $120. a. ___ units is the break-even quantity. (Type an integer) b. The profit for 470 units is $___ c. ___ units make a profit of $120. (Type an integer.)
Answers
The break-even quantity is 3 units. The profit for producing 470 units is $5624. 13 units must be produced for a profit of $120.here both cost and revenue are in dollars.
(a) To find the break-even quantity, we set the cost function C(x) equal to the revenue function R(x) and solve for x:
\(11x + 36 = 23x\)
\(36 = 12x\)
\(x = 3\)
Therefore, the break-even quantity is 3 units.
(b) The profit for producing 470 units can be calculated by subtracting the cost from the revenue:
\(Profit = Revenue - Cost\)
\(Profit = R(470) - C(470)\)
\(Profit = 23(470) - (11(470) + 36)\)
\(Profit = 10810 - 5186\)
\(Profit = $5624\)
The profit for producing 470 units is $5624.
(c) To find the number of units that must be produced for a profit of $120, we set the profit equation equal to $120 and solve for x:
\(Profit = Revenue - Cost\)
\($120 = R(x) - C(x)\)
\($120 = 23x - (11x + 36)\)
\($120 = 12x - 36\)
\(12x = 156\)
\(x = 13\)
Therefore, 13 units must be produced for a profit of $120.
Learn more about profit here:
https://brainly.com/question/12634106
#SPJ11
a house is advertised as having 1640 square feet under roof. what is the area of this house in square meters?
Answers
The area of this house in square meters is 152.24.
To convert square feet to square meters, you can use the conversion factor of 1 square foot = 0.092903 square meters.
A house is advertised as having 1640 square feet under the roof.
So, the area of the house in square meters is:
1640 square feet * 0.092903 square meters/square foot = 152.24 square meters.
Unit Conversion: It is defined as the changing from one quantity unit to another quantity unit followed by the method of division, and multiplication by a conversion factor.
Thus, the area of this house in square meters is 152.24 if the house is advertised as having 1640 square feet under the roof.
Learn more about the unit conversion here:
brainly.com/question/14350438
#SPJ4
Find the value of x. Please help :(

Answers
Answer:
x=100, hope this helped.
What is the longest increasing subsequence problem in dynamic programming?
Answers
The Longest Increasing Subsequence (LIS) problem is a classic problem in dynamic programming. Given a sequence of numbers, the problem is to find the longest subsequence in which the numbers are in increasing order. For example, given the sequence {3, 1, 5, 2, 4}, the longest increasing subsequence is {1, 2, 4}, which has length 3.
The LIS problem can be solved using dynamic programming by defining an array to store the length of the longest increasing subsequence that ends at each position in the sequence. The array is initialized to 1, and then for each position i in the sequence, the length of the longest increasing subsequence that ends at i is calculated by finding the maximum length of any subsequence that ends at a position j < i and has a smaller value than the value at i. The final solution is the maximum length of any subsequence in the array.
Find out more about dynamic programming
brainly.com/question/29809157
#SPJ4
21. A triangle has vertices A(-2,4), B(6,2), and C(1,-1). Prove using the Distance Formula and
Slope Formula that ABC is an isosceles right triangle.
Answers
To prove that triangle ABC is an isosceles right triangle, we need to show that two sides of the triangle are equal in length and one angle is a right angle.
Distance Formula:
The distance between two points (x₁, y₁) and (x₂, y₂) is given by the distance formula:
d = √[(x₂ - x₁)² + (y₂ - y₁)²]
Using the distance formula, we can calculate the lengths of the three sides of the triangle:
Side AB: d₁ = √[(6 - (-2))² + (2 - 4)²] = √[8² + (-2)²] = √(64 + 4) = √68
Side BC: d₂ = √[(1 - 6)² + (-1 - 2)²] = √[(-5)² + (-3)²] = √(25 + 9) = √34
Side AC: d₃ = √[(-2 - 1)² + (4 - (-1))²] = √[(-3)² + 5²] = √(9 + 25) = √34
Slope Formula:
The slope between two points (x₁, y₁) and (x₂, y₂) is given by the slope formula: m = (y₂ - y₁) / (x₂ - x₁)
Using the slope formula, we can calculate the slopes of the three sides of the triangle:
Slope AB:
m₁ = (2 - 4) / (6 - (-2)) = (-2) / 8 = -1/4
Slope BC:
m₂ = (-1 - 2) / (1 - 6) = (-3) / (-5) = 3/5
Slope AC:
m₃ = (4 - (-1)) / (-2 - 1) = 5 / (-3) = -5/3
From the distances calculated and the slopes of the sides, we can see that side AB is equal in length to side BC (both √34), indicating that two sides are equal. Additionally, the slope of side AC (m₃ = -5/3) is the negative reciprocal of the slope of side AB (m₁ = -1/4), indicating that the two sides are perpendicular, and hence, one angle is a right angle.
Therefore, triangle ABC is an isosceles right triangle.
Learn more about isosceles here
https://brainly.com/question/29793403
#SPJ11
If the area of square
A is 225 f12 and the
area of square B is 400
ft2, what is the area of
square C?

Answers
Answer:
Step-by-step explanation:
Square A:
Area = 225 square feet
side *side = 225
Side =√225
\(=\sqrt{15*15}\)
Side of square A = 15 ft
Square B:
Area = 400 square feet
Side =√400
= \(\sqrt{20*20}\)
Side of square B = 20 ft
Use Pythagorean theorem for finding the side of Square C.
Side of square A is the altitude ; side of square B is the base and side of square C will be the hypotenuse
hypotenuse² = base² + altitude²
= 15² + 20²
= 225 + 400
= 625
hypotenuse = \(\sqrt{625} =\sqrt{25*25}\) = 25 ft
Area of square C = 625 square ft
In short,
Area of square C = area of square B + area of square A
= 400 + 225
= 625 square ft
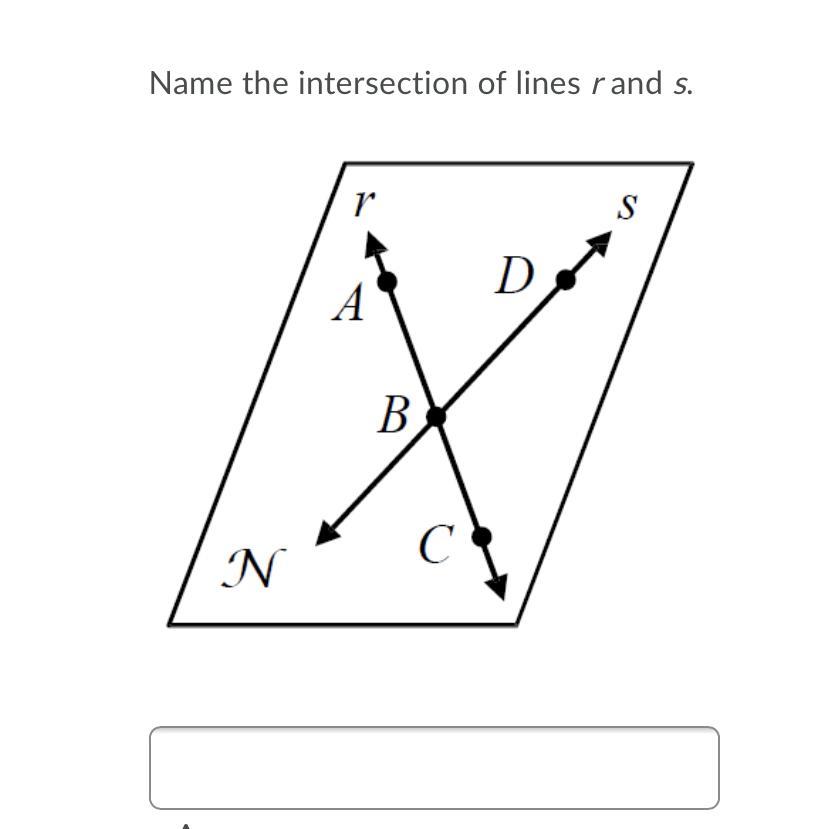
Name the intersection of lines r and s.
Answers
If three coins are thrown what is the probcbility Obtaining at least two head?
Answers
Answer:
2 head and 1 tail form my side
Paul’s mom needed a small carpet for the bathroom floor. There was room for a carpet that was 9/10 of a meter long and 4/5 of a meter wide. Choose the model that shows the area of the carpet.
options:
(the photos)
Answers
The area of the carpet is 9/10 square meters. Looking at the given options, we can see that only option (A) shows 9/10 square meters as the area of the carpet, so that is the correct answer.
The formula for the area A of a rectangle is: Area is a measure of the size of a two-dimensional surface, such as the surface of a square, rectangle, triangle, or circle. It is typically measured in square units, such as square meters, square feet, or square inches. The formula for calculating the area of a given shape depends on the shape itself.
A = length × width
In this case, the length of the carpet is 9/10 of a meter, and the width of the carpet is 4/5 of a meter.
Multiplying these values, we get:
A = (9/10) × (4/5)
To simplify this expression, we can first reduce the fractions:
A = (9/10) × (4/5)
A = (9/2) × (1/5)
A = (9/10)
To know more about meter here
https://brainly.com/question/1578784
#SPJ4
4+(−634) please answer
Answers
The solution to the expression 4+(−634) is -630
How to evaluate the expression?From the question, we have the following parameters that can be used in our computation:
4+(−634)
Rewrite the expression properly
So, we have the following representation
4 + (−634)
Remove the bracket in the above expression
This gives
4 + (−634) = 4 - 634
Evaluate the difference
4 + (−634) = -630
Hence, the solution is -630
Read more about expression at
https://brainly.com/question/15775046
#SPJ1
giving brainliest to the best answer

Answers
If two even integers are multiplied, then the product is also even. Hypothesis: Two even integers are multiplied. Hypothesis starts after the word "if". Conclusion starts after the word "then".
How do you identify a hypothesis and conclusion?The sentence that comes just after the word "if" in a conditional statement is known as the hypothesis. The sentence that comes after the word then in a conditional statement is the conclusion.
If you earn high grades, the portion that follows the "if" is referred to as a hypothesis, and if you get good grades, the part that follows the "then" is referred to as a conclusion.
An if-then statement, also known as a conditional statement, is a set of hypotheses followed by a conclusion.
p → q
Read this: if p, then q.
If the hypothesis is correct but the conclusion is untrue, a conditional statement is false. If the statement in the example above read, "If you achieve good marks then you will not get into a good college," it would be untrue.
To learn more about Hypothesis refer :
brainly.com/question/606806
#SPJ1
If two even integers are multiplied, then the product is also even. Hypothesis: Two even integers are multiplied. Hypothesis starts after the word "if". Conclusion starts after the word "then".
How do you identify a hypothesis and conclusion?The sentence that comes just after the word "if" in a conditional statement is known as the hypothesis. The sentence that comes after the word then in a conditional statement is the conclusion.
If you earn high grades, the portion that follows the "if" is referred to as a hypothesis, and if you get good grades, the part that follows the "then" is referred to as a conclusion.
An if-then statement, also known as a conditional statement, is a set of hypotheses followed by a conclusion.
p → q
Read this: if p, then q.
If the hypothesis is correct but the conclusion is untrue, a conditional statement is false. If the statement in the example above read, "If you achieve good marks then you will not get into a good college," it would be untrue.
To learn more about Hypothesis refer :
brainly.com/question/606806
#SPJ1
Which value for x proves that abc=def by sss

Answers
Answer:
7
Step-by-step explanation:
DE corresponds to AB.
37=5x+2
-2 -2
35=5x
7=x
50 POINTS WILL GIVE BRA1NLIEST

Answers
Answer:
Step-by-step explanation:
Answer
Likes music 60
Likes sports 26
Doesn't like 34
Does not like music 40
70% watch sports 28
Don't watch sports 12
===================================================
Comments
Those that like music have a total of 60
26 watch sports 60 - 26 = 34 do not watch sports
Those who do not like music are 100 - 60 = 40
Of the 40, 70/100 * 40 do watch sports = 28
The rest do not 12
Answer:
60 34 26
Step-by-step explanation:
I had the test once
Drag each tile to the table to multiply each row heading by
each column heading.

Answers
Answer:
Hey there!
4t(5t)=20t^2
4t(-4)=-16t
5(5t)=20t
5(-4)=-20
Hope this helps :)
Step-by-step explanation:
This is just a matter of multiplication. 4t x 5t = \(20t^{2}\), so that will be in your first box. 4t x -4 = -16t, so that'll be in your second box. 5 x 5t = 25t, so that will be in your bottom-first box, and 5 x -4 = -20, so that will be in your last one.
8 7 12 7 11
10 7 12
Find:
a)the median
b) the range
c)the mode
Answers
Answer:
a) Median: 9
b) Range: 5
c) Mode: 7
Step-by-step explanation:
The median is the number in the middle.
First, you put the numbers in order: 7, 7, 7, 8, 10, 11, 12, 12
The middle of this is 8 and 10, so you plus them and divide by to 2, then it gives 9, so the median is 9.
To find the range, you minus the highest number and the lowest number, 12-7=5.
Mode is the most occurring and repetitive number, in this case, 7, because it is written 3 times.
Hope this helps!!!
Answer:
\(\boxed{\mathrm {Median = 9}}\)
\(\boxed{\mathrm{Range = 5}}\)
\(\boxed{\mathrm{Mode = 7}}\)
Step-by-step explanation:
The observations are:
8,7,12,7,11,10,7,12
In ascending order:
=> 7,7,7,8,10,11,12,12
A) Median => Middlemost no.
Median = 8,10
=> \(\frac{8+10}{2}\)
=> \(\frac{18}{2}\)
Median = 9
B) Range = Highest No. = Lowest No.
RANGE = 12-7
Range = 5
C) Mode => frequently occurring number
Mode = 7
Find the gradient vector field of f.
f
(
x
,
y
)
=
y
sin
(
x
y
)
Answers
A gradient vector field of a function f(x,y) is a vector field that points in the direction of the greatest rate of increase of the function. In other words, the gradient vector field is the collection of all the gradient vectors of a function over a given domain.
The gradient vector field of f can be found by taking the partial derivatives of f with respect to x and y and constructing a vector field from these partial derivatives.
Here,
f(x,y) = ysin(xy),so we have
fx(x,y) = y*cos(xy)
fy(x,y) = sin(xy) + xy*cos(xy)
Thus, the gradient vector field of f is given by the vector field
F(x,y) = (y*cos(xy),
sin(xy) + xy*cos(xy))
This vector field can be visualized as a collection of vectors at each point (x,y) in the plane,
where the direction of the vector is determined by the partial derivatives and the magnitude of the vector represents the rate of change of the function in that direction.
Note that the gradient vector field is always perpendicular to the level curves of the function (i.e., the curves where f(x,y) is constant),
since the gradient vector points in the direction of greatest increase and the level curves are the contours where the function is constant.
Overall, the gradient vector field of
f(x,y) = ysin(xy) is
F(x,y) = (y*cos(xy), sin(xy) + xy*cos(xy)),
which is a vector field that represents the direction and rate of change of the function at each point in the plane.
To know more about gradient vectors visit:
https://brainly.com/question/29751488
#SPJ11
The number of people call 911 on March 25th?
A) continuous
B) discrete
C) categorical
Answers
Answer:
I think the answer is continuous hope this helps
Step-by-step explanation:
Also got subscribe to my YT channel BlxeVxbes
if you traveled in space at a speed of 1000 miles per house, how far would you travel in 7.5*10^5 houes
Answers
Traveling at a speed of 1000 miles per hour for 7.5 * 10⁵ hours would result in traveling a distance of 7.5 * 10⁸ miles.
To calculate the distance traveled, we can multiply the speed by the time traveled.
Speed = 1000 miles per hour
Time = 7.5 * 10⁵ hours
Distance = Speed * Time
Distance = 1000 miles/hour * 7.5 * 10⁵ hours
To perform this calculation, we can multiply the numerical values and keep the scientific notation for the result:
Distance = 1000 * 7.5 * 10⁵ miles
Distance = 7.5 * 10⁸ miles
Therefore, traveling at a speed of 1000 miles per hour for 7.5 * 10⁵ hours would result in traveling a distance of 7.5 * 10⁸ miles.
Learn more about Distance here
https://brainly.com/question/18815731
#SPJ4
The table shows the number of blue marbles and red marbles that four friends have collected.
Blue and Red Marbles
Blue
Red
Jasmine
12
10
Aaron
3
2
Lucian
10
10
Gretchen
14
2
Which person has the highest ratio of blue to red marbles?
Answers
Answer:
Gretchen
Step-by-step explanation: This is since 14 to 2 is saying that gretchen has 7 times the blue marbles than red
Please help. I don’t fully understand yet!

Answers
The surface area of the cylinders are: 7794 square units, 904.9 square units, 12804 square units
What is a cylinder?recall that a cylinder is a three-dimensional solid with two parallel circular bases joined by a curved surface at a fixed distance from the center. It is considered a prism with a circle as its base and is a combination of two circles and a rectangle
the general formula for the surface area of a cylinder is
SA = 2пr(r+h)
1 SA =2*22/7*20 (20+42)
125.7(62)
SA = 7794 square units
2) SA = 2пr(r+h)
Sssurface rea = 2*3.142*9(9+7)
Surface area = 56.6(16)
Surface area = 904.9 square units
3) SA = 2пr(r+h)
surface area = 2*3.142*21(21+76)
Surface area = 132(97)
Surface area = 12804 square units
Learn more about surface area of cylinders on https://brainly.com/question/29015630
#SPJ1
Please help.
Is algebra.
PLEASE HELP NO LINKS OR FILES.
I don't want links.

Answers
Question 2: Answer D - IV, I, II, III
Locksmith Larry charges $90 for a house call plus $20 per hour. Locksmith Barry charges $50 for a house call plus $30 per hour. Write a one-variable equation for the charges of locksmith Larry
Answers
Answer:
Barry: g(x) = 50 + 30x
Larry: f(x) = 90 + 20x
If Locksmith Larry charges $90 for a house call plus $20 per hour. Locksmith Barry charges $50 for a house call plus $30 per hour. Then f(x)=90+20x is one-variable equation for the charges of locksmith Larry
What is Equation?Two or more expressions with an Equal sign is called as Equation.
Given,
Locksmith Larry charges $90 for a house call plus $20 per hour
f(x) represents this situation
f(x) equal to ninety plus twenty times of x
f(x)=90+20x
Locksmith Barry charges $50 for a house call plus $30 per hour
g(x) represents this situation
g(x) equal to fifty plus thirty times of x
g(x)=50+30x
Here x represents the number of hours
Hence f(x)=90+20x is the one-variable equation for the charges of locksmith Larry
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ5
A certain circle can be represented by the following equation. x^2+y^2+8x-16y+31=0x 2 +y 2 +8x−16y+31=0x, squared, plus, y, squared, plus, 8, x, minus, 16, y, plus, 31, equals, 0 What is the center of this circle ? ((left parenthesis ,,comma ))right parenthesis What is the radius of this circle ? units
Answers
Answer:
center = \((-4,8)\)
Radius = 7 units
Step-by-step explanation:
Given: Equation of circle is \(x^2+y^2+8x-16y+31=0\)
To find: Radius and center of the circle
Solution:
Equation of circle is \((x-a)^2+(y-b)^2=r^2\)
Here, \((a,b)\) is the center and r is the radius.
\(x^2+y^2+8x-16y+31=0\\\left [ x^2+2(4)x+4^2 \right ]+\left [ y^2-2(8)y+8^2 \right ]+31=4^2+8^2\)
Use formula \((u+v)^2=u^2+v^2+2uv\)
\((x+4)^2+(y-8)^2=16+64-31\\(x+4)^2+(y-8)^2=49=7^2\)
On comparing this equation with equation of circle,
center = \((-4,8)\)
Radius = 7 units
Answer:
center: (4,-4)
Radius: 9
Step-by-step explanation:
KHAN ACADEMY
Consider the PDE au(x, t) = 4 d²u(x, t) 2 Ət əx² For each of BCs and ICs, solve the initial value problem. du(π,t) a) BCs: u(0,t)=0 = = 0 and əx IC: u(x,0) = x ANSWER: f(x)= n=1 u(2,t) = 0 and u(0,t)=0 u(x,0)=sin x ANSWER: f(x)=¹1_sin(2 + nx) na n=1 1+ 2 X b) BCs: IC: 8 (2n-1) T n+1 (-1)041 -4(2n-1)²t sin(2-nπ) nπ 1- 2 e sin (2n-1) 2 na sin X 2 -(nn)²t x -X
Answers
the solution for the initial value problem is: u(x, t) = sin(sqrt(-λ² * (a / 4)) * x) * exp(-λ² * t) where λ = ± sqrt(-4n² / a), and n is a non-zero integer.
The given partial differential equation is:
au(x, t) = 4 * (d²u(x, t) / dt²) / (dx²)
a) BCs (Boundary Conditions):
We have u(0, t) = 0 and u(π, t) = 0.
IC (Initial Condition):
We have u(x, 0) = x.
To solve this initial value problem, we need to find a function f(x) that satisfies the given boundary conditions and initial condition.
The solution for f(x) can be found using the method of separation of variables. Assuming u(x, t) = X(x) * T(t), we can rewrite the equation as:
X(x) * T'(t) = 4 * X''(x) * T(t) / a
Dividing both sides by X(x) * T(t) gives:
T'(t) / T(t) = 4 * X''(x) / (a * X(x))
Since the left side only depends on t and the right side only depends on x, both sides must be equal to a constant value, which we'll call -λ².
T'(t) / T(t) = -λ²
X''(x) / X(x) = -λ² * (a / 4)
Solving the first equation gives T(t) = C1 * exp(-λ² * t), where C1 is a constant.
Solving the second equation gives X(x) = C2 * sin(sqrt(-λ² * (a / 4)) * x) + C3 * cos(sqrt(-λ² * (a / 4)) * x), where C2 and C3 are constants.
Now, applying the boundary conditions:
1) u(0, t) = 0:
Plugging in x = 0 into the solution X(x) gives C3 * cos(0) = 0, which implies C3 = 0.
2) u(π, t) = 0:
Plugging in x = π into the solution X(x) gives C2 * sin(sqrt(-λ² * (a / 4)) * π) = 0. To satisfy this condition, we need the sine term to be zero, which means sqrt(-λ² * (a / 4)) * π = n * π, where n is an integer. Solving for λ, we get λ = ± sqrt(-4n² / a), where n is a non-zero integer.
Now, let's find the expression for u(x, t) using the initial condition:
u(x, 0) = X(x) * T(0) = x
Plugging in t = 0 and X(x) = C2 * sin(sqrt(-λ² * (a / 4)) * x) into the equation above, we get:
C2 * sin(sqrt(-λ² * (a / 4)) * x) * C1 = x
This implies C2 * C1 = 1, so we can choose C1 = 1 and C2 = 1.
Therefore, the solution for the initial value problem is:
u(x, t) = sin(sqrt(-λ² * (a / 4)) * x) * exp(-λ² * t)
where λ = ± sqrt(-4n² / a), and n is a non-zero integer.
Note: Please double-check the provided equation and ensure the values of a and the given boundary conditions are correctly represented in the equation.
To know more about Equation related question visit:
https://brainly.com/question/29657983
#SPJ11
How do you simplify and verify trig identities?
Answers
In order to simplify and verify trig identities, one needs to use the rules of trigonometry and algebra to manipulate the equation until it is in a simplified form.
The most common trig identities to remember include the Pythagorean identity, reciprocal identities, quotient identities, and sum and difference identities. When simplifying an equation, it is important to remember to include the negative sign when necessary and to factor out any common factors.
After simplifying, it is important to verify the equation. This can be done by plugging in known values for the variables and verifying that the equation is true. By utilizing the rules of trigonometry and algebra, one can simplify and verify trig identities. This process is essential for working with trigonometric functions.
know more about algebra here
https://brainly.com/question/24875240#
#SPJ11
Which set of numbers can represent the side lengths, in inches, of an acute triangle?
o 4,5,7
O 5,7,8
O 6,7, 10
O 7.9, 12
Answers
Answer:
5 , 7 , 8 represent the side of acute angled triangle
Set B with sides 5 , 7 , 8 represent the side of acute angled triangle.
What is mean by Triangle?A triangle is a three sided polygon, which has three vertices and three angles which has the sum 180 degrees.
Given that:
Set of numbers.
Now, We use the following result:
When given 3 triangle sides then to determine if the triangle is acute angled , right angled or obtuse angled.
First find Square all 3 sides, then Sum the squares of the 2 shortest sides and then Compare the sum to the square of the last side.
if sum > Square of last side ⇒ it is Acute Triangle
if sum = Square of last side ⇒ it is Right Triangle
if sum < Square of last side ⇒ it is Obtuse Triangle
a). 4 , 5 , 7
4² = 16 , 5² = 25 , 7² = 49
16 + 25 = 41
Hence, 41 < 49
⇒ It is an Obtuse Triangle.
b). 5 , 7 , 8
5² = 25 , 7² = 49 , 8² = 64
25 + 49 = 74
Hence, 74 > 64
⇒ It is an acute Triangle.
c). 6 , 7 , 10
6² = 36 , 7² = 49 , 10² = 100
36 + 49 = 85
Hence, 85 < 100
⇒ It is an Obtuse Triangle.
d). 7 , 9 , 12
7² = 49 , 9² = 81 , 12² = 144
49 + 81 = 130
Hence, 130 < 144
⇒ It is an Obtuse Triangle.
Therefore, Set B with sides 5 , 7 , 8 represent the side of acute angled triangle.
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ7