Solve the equation for a
5n + 34 = -2(1 - 7n)
a equals
Answers
Answer:
n = 4
Step-by-step explanation:
Where's a or did you mean n?
Answer:
n=4
Step-by-step explanation:
5n+34=-2(1-7n)
1. So first expand.
5n+34=−2+14n
2 Regroup terms.
5n+34=14n−2
3 Subtract 5n from both sides.
34=14n−2−5n
4 Simplify 14n-2-5n to 9n-2.
34=9n−2
5 Add 22 to both sides.
34+2=9n
6 Simplify 34+2 to 36.
36=9n
7 Divide both sides by 9.
36/9=9
8 Simplify 36/9 to 4
4=n
9 Switch sides.
n=4
Related Questions
Analyzing the y-intercept

Answers
Answer:
The value of b to 2
Step-by-step explanation:
This causes the graph to go down 3 units because the one ordered to the origin (b) was initially at 5 and when subtracting three it goes down to 2
I hope this help you
(No joke answers)
A savings account pays a 3% nominal annual interest rate and
has a balance of$1,000. Any interest earned is deposited into
the account and no further deposits or withdrawals are made.
If interest is compounded semi-annually (every six months),
what interest rate would be used for each calculation?
O 0. 5%
O 3%
0 1. 5%
6%
Answers
The interest rate used for each semi-annual calculation for a savings account with a nominal annual interest rate of 3% and balance of $1,000, compounded semi-annually, is option (b) 3%
If the nominal annual interest rate is 3%, and interest is compounded semi-annually, then we need to find the semi-annual interest rate.
The formula for calculating the effective interest rate for a given nominal interest rate compounded semi-annually is
r = (1 + (i/n))^(n/t) - 1
Where:
r = the semi-annual interest rate
i = the nominal annual interest rate (as a decimal)
n = the number of times interest is compounded per year (in this case, 2)
t = the time period over which interest is calculated (in this case, 1 year)
Plugging in the values, we get
r = (1 + (0.03/2))^(2/1) - 1
r = (1 + 0.015)² - 1
r = 0.03
t = 3%
Therefore, the correct option is (b) 3%
Learn more about interest rate here
brainly.com/question/30573341
#SPJ4
3.5 x 10^3 divided by 7 x 10^-2
Answers
Answer:
5 · \(10^{4}\)
Step-by-step explanation:
(✿◡‿◡) <--- she wants Brainliest
Answer: 3.5 times 10^3 is the same as 3.5 times 1000 so you get 3,500 now 7 times 10^-2 is the same as 7 times 1/100 and you get 7/100 so now we can divide 3,500 divided by 7/100 and we get 50,000
Step-by-step explanation:
Question 7 of 25
URGENT! PLEASE ANSWER
Which of these changes
produces a chemical change?
A. A large rock is crushed into gravel.
B. Lava cools and changes from a thick fluid to solid rock.
C. A stone fizzes and forms a gas when acid is dropped on it.
D. Limestone slowly dissolves in water and forms a cave.
Answers
Answer:
Answer is C.
Step-by-step explanation:
it changes the CHEMICAL composition of it
What is 2/3x + y = 2 graphed?
Answers
y=-2/3x+2
16,000 lb = _______ T
If you are able to help please do! <3 it’s highly appreciated
Answers
Answer:
\(8\) tons
Step-by-step explanation:
Divide the mass value by 2000, easy.
Answer:
IT'S
7.143 Tons
Step by Step:
For an approximate result,
divide the mass value by 2205
Eva invested $500 in an account paying an interest rate of 4 5/8% compounded daily.
Amira invested $500 in an account paying an interest rate of 4 3/4% compounded
monthly. After 15 years, how much more money would Amira have in her account
than Eva, to the nearest dollar?
Answers
The total amount accrued of Eva principal plus interest, with compound interest on a principal of $500.00 at a rate of 4% per year compounded 365 times per year over 15 years is $911.03.
The total amount accrued of Amira principal plus interest, with compound interest on a principal of $500.00 at a rate of 4% per year compounded 12 times per year over 15 years is $910.15.
Compounded interest adds interest not only to your principle amount, but your accumulated interest over time.
To calculate compound interest we use the formula below where A = total balance after t years, P = principal amount (amount borrowed or invested), r = interest rate (decimal form), and t = time in years.
Eva invested $500 in an account paying an interest rate of 4 5/8% compounded daily.
A = $911.03
A = P + I where
P (principal) = $500.00
I (interest) = $411.03
First, convert R as a percent to r as a decimal
r = R/100
r = 4/100
r = 0.04 rate per year,
Then solve the equation for A
A = P(1 + r/n)nt
A = 500.00(1 + 0.04/365)(365)(15)
A = 500.00(1 + 0.00010958904109589)(5475)
A = $911.03
Hence, The total amount accrued of Eva principal plus interest, with compound interest on a principal of $500.00 at a rate of 4% per year compounded 365 times per year over 15 years is $911.03.
Amira invested $500 in an account paying an interest rate of 4 3/4% compounded monthly.
Given Principal (P) = $500
Interest rate (r) = 6%
Time (t) = 15 years
By taking compound interest formula:
\(A = P(1+\frac{r}{n} )^{\frac{n}{t} }\)
First, convert R as a percent to r as a decimal
r = R/100
r = 4/100
r = 0.04 rate per year,
Then solve the equation for A
\(A = P(1+\frac{r}{n})^{\frac{n}{t} }\)
A = 500.00(1 + 0.04/12)(12)(15)
A = 500.00(1 + 0.0033333333333333)(180)
A = $910.15
Hence the answer is, The total amount accrued, principal plus interest, with compound interest on a principal of $500.00 at a rate of 4% per year compounded 12 times per year over 15 years is $910.15.
To learn more about compound interest click here https://brainly.com/question/28020457
#SPJ1
Answer:18
Step-by-step explanation:
Please someone help me. Im giving brainliest!!!

Answers
Answer:
Step-by-step explanation:
b
What is the intersection of two planes 1⃣ point 2⃣ segment 3⃣ straight line 4⃣ plane?
Answers
the intersection of two planes 1⃣ point 2⃣ segment 3⃣ straight line 4⃣ plane has The intersection of two planes is a straight line.
When two planes intersect each other, the intersection of two plane is a line. This line is formed by the points that satisfy the equations of the two planes.When two planes intersect each other, their intersection is a straight line. This line is determined by the points which are common to both planes and which satisfy the equations of the two planes. The line is the shortest path between any two points on the surface of the planes.
Learn more about intersection of two plane here
https://brainly.com/question/9462569
#SPJ4
if q is the point x, 4 3 − x , find the slope of the secant line pq (correct to six decimal places) for the following values of x.
Answers
You can find the slope of the secant line PQ for other values of x by substituting them into the expression for the slope:
For x = 2:
slope = -1 / (3 - 2(2))
slope = -1 / (3 - 4)
slope = -1 / (-1)
slope = 1
To find the slope of the secant line PQ, we need two points on the line: P(x, 4) and Q(3 - x, 3).
The slope of a line passing through two points (x1, y1) and (x2, y2) is given by the formula:
slope = (y2 - y1) / (x2 - x1)
In this case, the coordinates of P are (x, 4) and the coordinates of Q are (3 - x, 3). Plugging these values into the slope formula, we have:
slope = (3 - 4) / (3 - x - x)
slope = -1 / (3 - 2x)
To find the slope of the secant line for different values of x, we substitute those values into the expression for the slope.
For example, if x = 1, the slope of the secant line PQ is:
slope = -1 / (3 - 2(1))
slope = -1 / (3 - 2)
slope = -1 / 1
slope = -1
Similarly, you can find the slope of the secant line PQ for other values of x by substituting them into the expression for the slope:
For x = 2:
slope = -1 / (3 - 2(2))
slope = -1 / (3 - 4)
slope = -1 / (-1)
slope = 1
And so on, you can calculate the slope of the secant line for different values of x.
Learn more about expression from
brainly.com/question/1859113
#SPJ11
Which expression below is equivalent to 1/2x-1/8
a. 2(x-1/8)
b. 1/2(x-1/4)
c. 1/2(x-1/8)
d. 1/4(1/2x-1/2)
Answers
1/2(x-1/4)
Distribute 1/2(x) and 1/2(1/4)
19. A soccer field is a rectangle 90 meters wide and 120 meters long. If you were
asked to run from one corner to the other corner diagonally across, what is the
distance?
a. 150 meters
b. 1500 meters
c. 15 meters
d. 200 meters
Answers
90x90=8100
14400+8100=22500
Square root of 22500=150
Hope this helps!
Maura spends $5.50 in materials to make a scarf. She sells each scarf for 600% of the cost of materials.
Complete the sentence by selecting the correct word from the drop down choices.
Maria sells each scarf for Choose... ✓ or

Answers
The price that Maura sell each scarf would be =$33. Maura sells each scarf for $33. That is option A.
How to calculate the selling price of each scarf?To calculate the amount of money that Maura spends on each scarf the following is carried out.
The amount of money that she spends on the scarf material = $5.50
The percentage selling price of each scarf = 600% of $5.50
That is ;
= 600/100 × 5.50/1
= 3300/100
= $33.
Therefore, each price that is sold by Maura would probably cost a total of $33.
Learn more about cost price here:
https://brainly.com/question/26008313
#SPJ1
PLEASE HELP MEEE I DONT GET THISSSSS

Answers
Answer:
Root is a fancy word for a zero.
Using the quadratic formula you will get
x = 1.2, -.25
B is the correct answer. (-1/4)
what is the value of x

Answers
Answer: x⁰ = 104⁰
Ok done. Thank to me :>

In ΔTUV, the measure of ∠V=90°, UT = 65, VU = 56, and TV = 33. What ratio represents the cosine of ∠T?
Answers
Answer: \(\frac{33}{65}\)
Step-by-step explanation:
cosine of ∠T = \(\frac{adjacent}{hypotenuse}\)
For ∠T,
Adjacent side = 33Hypotenuse = 65cosine of ∠T = \(\frac{33}{65}\)

The value of the trigonometric relation cos ∠T = 0.507
What are trigonometric relations?Trigonometry is the study of the relationships between the angles and the lengths of the sides of triangles
The six trigonometric functions are sin , cos , tan , cosec , sec and cot
Let the angle be θ , such that
sin θ = opposite / hypotenuse
cos θ = adjacent / hypotenuse
tan θ = opposite / adjacent
tan θ = sin θ / cos θ
cosec θ = 1/sin θ
sec θ = 1/cos θ
cot θ = 1/tan θ
Given data ,
Let the triangle be represented as ΔTUV
where the measure of ∠UVT = 90°
And , the measure of side UT = 65 units
The measure of VU = 56 units
And , the measure of TV = 33 units
From the trigonometric relations ,
cos θ = adjacent / hypotenuse
On simplifying , we get
cos ∠T = TV / UT
cos ∠T = 33 / 65
cos ∠T = 0.50769
Hence , the trigonometric relation is solved
To learn more about trigonometric relations click :
https://brainly.com/question/14746686
#SPJ2
4.5. Let N be a nonnegative integer-valued random variable. For nonnegative values aj.J > = I. show that Then show that and
Answers
We have shown that P(N < aJ) ≤ 1 - J for nonnegative values aj.N is a nonnegative integer-valued random variable
To prove the given inequality, let's start by defining the indicator random variable Ij, which takes the value 1 if aj ≤ N and 0 otherwise.
We have:
Ij = {1 if aj ≤ N; 0 if aj > N}
Now, we can express the expectation E(Ij) in terms of the probabilities P(aj ≤ N):
E(Ij) = 1 * P(aj ≤ N) + 0 * P(aj > N)
= P(aj ≤ N)
Since N is a nonnegative integer-valued random variable, its probability distribution can be written as:
P(N = n) = P(N ≤ n) - P(N ≤ n-1)
Using this notation, we can rewrite the expectation E(Ij) as:
E(Ij) = P(aj ≤ N) = P(N ≥ aj) = 1 - P(N < aj)
Now, let's consider the sum of the expectations over all values of j:
∑ E(Ij) = ∑ (1 - P(N < aj))
Expanding the sum, we have:
∑ E(Ij) = ∑ 1 - ∑ P(N < aj)
Since ∑ 1 = J (the total number of values of j) and ∑ P(N < aj) = P(N < aJ), we can write:
∑ E(Ij) = J - P(N < aJ)
Now, let's look at the expectation E(∑ Ij):
E(∑ Ij) = E(I1 + I2 + ... + IJ)
By linearity of expectation, we have:
E(∑ Ij) = E(I1) + E(I2) + ... + E(IJ)
Since the indicator random variables Ij are identically distributed, their expectations are equal, and we can write:
E(∑ Ij) = J * E(I1)
From the earlier derivation, we know that E(Ij) = P(aj ≤ N). Therefore:
E(∑ Ij) = J * P(a1 ≤ N) = J * P(N ≥ a1) = J * (1 - P(N < a1))
Combining the expressions for E(∑ Ij) and ∑ E(Ij), we have:
J - P(N < aJ) = J * (1 - P(N < a1))
Rearranging the terms, we get:
P(N < aJ) = 1 - J * (1 - P(N < a1))
Since 1 - P(N < a1) ≤ 1, we can conclude that:
P(N < aJ) ≤ 1 - J
Therefore, we have shown that P(N < aJ) ≤ 1 - J for nonnegative values aj.
Learn more about Probabilities here,https://brainly.com/question/13604758
#SPJ11
Consider a competitive industry with a large number of firms, all of which have identical cost functions c(y) = 2y² +8 for y> 0 and c(0) = 0. Marginal cost is MC(y) = 4y. Suppose that initially the demand curve for this industry is given by D(p) = 20 - p (The output of a firm does not have to be an integer number, but the number of firms does have to be an integer) (a) What is the supply curve of an individual firm? If there are n firms in the industry, what will be the industry supply curve? (b) What is the smallest price at which the product can be sold? (c) What will be the equilibrium number of firms in the industry? equilibrium price? What will be the equilibrium output of each firm? equilibrium output of the industry? (d) Now suppose that the demand curve shifts to D(p) = 21 p. What will be the equilibrium number of firms? (Hint: Can a new firm enter the market and make nonnegative profits?) (e) With the new demand curve D(p) 21 p, what will be the equilibrium price? What will be the equilibrium output of each firm? What will be the equilibrium output of the industry? (f) Now suppose that the demand curve shifts to D(p) = 24 - p. What will be the equi- librium number of firms? What will be the equilibrium price? What will be the equilibrium output of each firm? What will be the equilibrium profits of each firm? = What will be the What will be the
Answers
The equilibrium number of firms will be the smallest integer such that the price is 6 or higher. This occurs when n = 2. At this equilibrium, the price is P = 6, the output of each firm is y = 3/2, the industry's output is Y = 3, and the profit of each firm = -2.
a) Supply curve of an individual firm
The price received by the individual firm will be P. Its demand curve is given by
D(p) = 20 - p.
Each firm chooses output to maximize its profit. Profit maximization occurs when the price is equal to the marginal cost. Mathematically,
P = MC(y)
4y = P
y = P/4
Thus the supply curve of the firm is y = P/4
b) The smallest price at which the product can be sold. The product can be sold at the minimum of the supply curve, which is y = 0, given P ≥ 0. Therefore the smallest price is P = 0.
c) Equilibrium price and output
Equilibrium occurs when each firm is producing at its profit-maximizing output given the output of other firms. Let the number of firms in the industry be n. The output of the industry is Y = ny. The industry supply curve is given by
S(P) = nP/4
The equilibrium price intersects the industry supply curve with the demand curve. Thus the equilibrium price satisfies
S(P) = Y
nP/4 = 20 - P
=> P = 80/(4 + n).
The equilibrium number of firms is the number that makes the industry supply curve equal to the demand curve. Thus
20 - P = nP/4
=> P = 80/(4 + n)
=> n = (80 - 20P)/P
= 20/P - 4.
Thus the equilibrium number of firms is a function of P and can range between 1 and infinity, but it must be an integer. The equilibrium output of each firm is given by
y = P/4 = 20/(4n + n²)
The equilibrium output of the industry is given by
Y = n
y = 5/P = (n² + 4n)/80.
d) Equilibrium number of firms with new demand curve D(p) = 21 - p.
The intersection of this curve with the marginal cost curve is at p = 21/5. This is greater than the minimum possible price of 0. Thus there is a positive profit to be earned in this industry, and new firms can enter the market.
e) Equilibrium price and output with new demand curve with the new demand curve D(p) = 21 - p, the industry supply curve and the equilibrium price are as given in part (d). The equilibrium output of each firm is given by y = P/4 = 21/20, and the equilibrium output of the industry is given by Y = 21/4.
f) Equilibrium number of firms, price, output, and profit with demand curve D(p) = 24 - p. This demand curve intersects the marginal cost curve at p = 6. The minimum possible price is P = 0. Thus there is a range of prices from 0 to 6 where firms can profit positively.
The equilibrium number of firms will be the smallest integer such that the price is 6 or higher. This occurs when n = 2. At this equilibrium, the price is P = 6, the output of each firm is y = 3/2, the output of the industry is Y = 3, and the profit of each firm is (6)(3/2) - (2)(2(3/2)² + 8) = -2.
To know more about the demand curve, visit:
brainly.com/question/13131242
#SPJ11
This laboratory experiment requires the simultaneous solving of two equations each containing two unknown variables. There are two mathematical methods to do this. One: rearrange one equation to isolate one variable (eg, AH = ...), then substitute that variable into the second equation. Method two: subtract the two equations from each other which cancels out one variable. Prepare by practicing with the data provided below and use equation 3 to solve for AH, and AS. Temperature 1 = 15K Temperature 2 = 75 K AG= - 35.25 kJ/mol AG= -28.37 kJ/mol
Answers
The values for AH and AS using the given data and the two methods described are:
AH = -36.4 kJ/mol.
AS = -0.115 kJ/(mol*K),
How to solve for AH and As using the two methods?We shall apply the two provided methods to solve for AH and AS on the provided data.
Method One:
We'll use the Gibbs free energy equation:
ΔG = ΔH - TΔS
where:
ΔG = change in Gibbs free energy,
ΔH = change in enthalpy,
ΔS = change in entropy,
T= temperature in Kelvin.
Given:
T1 = 15 K
T2 = 75 K
ΔG1 = -35.25 kJ/mol
ΔG2 = -28.37 kJ/mol
We set up two equations using the provided data:
Equation 1: ΔG1 = ΔH - T1ΔS
Equation 2: ΔG2 = ΔH - T2ΔS
Method Two:
We subtract Equation 1 from Equation 2 to eliminate ΔH:
ΔG2 - ΔG1 = (ΔH - T2ΔS) - (ΔH - T1ΔS)
ΔG2 - ΔG1 = -T2ΔS + T1ΔS
ΔG2 - ΔG1 = (T1 - T2)ΔS
Now we have two equations:
Equation 3: ΔG1 = ΔH - T1ΔS
Equation 4: ΔG2 - ΔG1 = (T1 - T2)ΔS
Next, we solve these equations to find the values of AH and AS.
Plugging in the values from the given data into Equation 3:
-35.25 kJ/mol = AH - 15K * AS
AH = -35.25 kJ/mol + 15K * AS
Put the values from the given data into Equation 4:
(-28.37 kJ/mol) - (-35.25 kJ/mol) = (15K - 75K) * AS
6.88 kJ/mol = -60K * AS
So, we got two equations:
Equation 5: AH = -35.25 kJ/mol + 15K * AS
Equation 6: 6.88 kJ/mol = -60K * AS
We can solve these two equations simultaneously to find the values of AH and AS.
Substituting Equation 6 into Equation 5:
AH = -35.25 kJ/mol + 15K * (6.88 kJ/mol / -60K)
AH = -35.25 kJ/mol - 1.15 kJ/mol
AH = -36.4 kJ/mol
Put the value of AH into Equation 6:
6.88 kJ/mol = -60K * AS
AS = 6.88 kJ/mol / (-60K)
AS = -0.115 kJ/(mol*K)
So, AH = -36.4 kJ/mol and AS = -0.115 kJ/(mol*K).
Learn more about Gibbs free energy equation at brainly.com/question/9179942
#SPJ4
for a second-order homogeneous linear ode, any linear combination of two solutions on an open interval i need not be a solution of the ode on i. TRUE OR FALSE?
Answers
The statement "for a second-order homogeneous linear ode, any linear combination of two solutions on an open interval i need not be a solution of the ode on" provided is actually FALSE.
For a second-order homogeneous linear ODE, any linear combination of two solutions on an open interval is indeed a solution of the ODE on that interval.
Let y1(x) and y2(x) be two solutions of a second-order homogeneous linear ODE on an open interval I. Then, the ODE can be written in the form:
\(L[y] = y''(x) + p(x)y'(x) + q(x)y(x) = 0\)
where L is a linear differential operator, p(x) and q(x) are continuous functions on I.
Since y1(x) and y2(x) are solutions, we have:
L[y1] = 0 and L[y2] = 0
Now consider any linear combination of y1(x) and y2(x):
y(x) = C1*y1(x) + C2*y2(x)
where C1 and C2 are constants. Let's apply the linear operator L to this linear combination:
L[y] = L[C1*y1(x) + C2*y2(x)]
Using the linearity property of the operator L, we have:
L[y] = C1*L[y1] + C2*L[y2]
Since L[y1] = 0 and L[y2] = 0:
L[y] = C1*0 + C2*0 = 0
Thus, y(x) is also a solution of the second-order homogeneous linear ODE on the open interval I.
To know more about second-order homogeneous linear ODE, refer here:
https://brainly.com/question/31399883
#SPJ11
What is the value of x? What is the length of MN
Please explain how you got the answer.
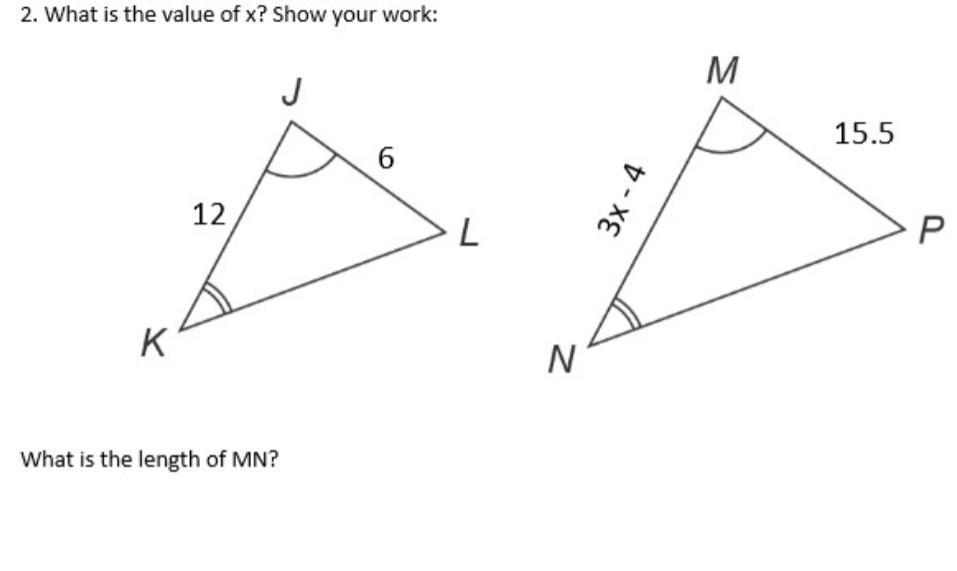
Answers
Answer:
x=35/3
Step-by-step explanation:
The two triangles are similar
So the equation is
12/6=3x-4/15.5
2=3x-4/15.5
3x-4=31
3x=35
x=35/3
Square WXYZ has coordinates W(-4, 5), X(-1, 5), Y(-1, 8), and Z(-4, 8). If the square is translated 1 unit left and 1 unit up, what are the coordinates of W'?
Answers
Answer:
it would be (-5,6) your welcome
I WILL GIVE BRAINRLY

Answers
Answer:
a
Step-by-step explanation:
f(x)-g(x)=2x square-3x+6-(3x square +4x-8)
2x square-3x+6-3x square-4x+8
-x square-7x+14
McKenna and Lara work for their uncle Eddie, who repairs skateboards and bicycles. Uncle Eddie is leaving for a vacation to the Amazon. He asks the girls to order 54 new wheels for the 21 skateboards and bicycles in his repair shop. How many bicycles and how many skateboards are in Uncle Eddie's shop? From the list of facts, circle those you need to solve Lara and McKenna's problem. McKenna and Lara's uncle is named Eddie. There are 21 skateboards and bicycles in the shop. Uncle Eddie went on a trip. A bicycle has two wheels, and a skateboard has four wheels. 54 new wheels are needed. How many bicycles and how many skateboards are in the shop? Show your work.
Answers
Answer:
There are 21 skateboards and bicycles in the shop.
A bicycle has two wheels, and a skateboard has four wheels
54 new wheels are needed
Number of bicycles = 15
Number of skateboards = 6
Step-by-step explanation:
Number of bicycles and skateboards = 21
Number of new wheels ordered = 54
Number of wheels in a bicycle = 2
Number of wheels in a skateboard = 4
Number of skateboards and bicycles in shop?
Let number of bicycles = b
Number of skateboards = s
b + s = 21 - - - (1)
(2*b) + (4*s) = 54
2b + 4s = 54 - - - - - - (2)
From (1)
b = 21 - s
2(21 - s) + 4s = 54
42 - 2s + 4s = 54
42 + 2s = 54
2s = 54 - 42
2s = 12
s = 6
From : b = 21 - s
b = 21 - 6
b = 15
Number of bicycles = 15
Number of skateboards = 6
24.7% of the products in the local shop are specialty soaps. 76% of those soaps are made with fresh herbs. if there are 350 bars of specialty soap in the shop, approximately how many of them are not made with fresh herbs? round your answer up to nearest whole number
Answers
we know that 76% of the specialty soaps are made with fresh herbs, and we also know that there are a total of 350 specialty soap bars, so how many are made with fresh herbs? well, just 76% of those 350
\(\begin{array}{|c|ll} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{76\% of 350}}{\left( \cfrac{76}{100} \right)350}\implies 266\)
Please Help me - You will get 60 points for the rapid reply- Use isosceles trapezoid ABCD to determine the following measurements-

Answers
Answer:
1) AD = 9 in
2) DE = 9.25 in
3) ∠EDC = 36°
4) ∠AEB = 108°
5) 11.5 in
Step-by-step explanation:
1) AD = BC = 9in
2) AC = BD (diagonals are equal)
⇒ BD = 14.25
⇒ BE + DE = 14.25
⇒ 5 + DE = 14.25
DE = 9.25
3) Since AB ║CD,
∠ABE = ∠EDC = 36°
4) ∠ABE = ∠BAE = 36°
Also ∠ABE + ∠BAE + ∠AEB = 180 (traingle ABE)
⇒ 36 + 36 + ∠AEB = 180
∠AEB = 108
5) midsegment = (AB + CD)/2
= (8 + 15)/2
11.5
PLEASE PLEASE HELP! QUICKLY!

Answers
Step-by-step explanation:
we have
m∠3 = 128°
m∠3 = m∠7---------------- > Corresponding Angles
180°=m∠7+m∠8---------- > Supplementary Angles
therefore
m∠8=180°-128°=52°
the answer is the m∠8 is 52°
Liv earns $9.50 for every two bracelets she sells. The equation y = 4.75x can be used to represent this situation.
What is the constant of proportionality? Express your answer in decimal form.
Answers
Answer:
2.58
Step-by-step explanation:
In the terminal side of an angle in standard position lies on -4y=3x and x>0, find the exact values of the trigonometric functions of 0
Answers
Answer:
sec ∅ = 5/4
cosec ∅ = -5/3
cot ∅ = -4/3
Tan ∅ = - 3/4
sin ∅ = -3/5
cos ∅ =4/5
Step-by-step explanation:
Given : -4y = 3x , x > 0
i.e. 3x + 4y = 0 , x >0
4y = -3x ∴ y = - 3/4 x
The values of trigonometric functions of ∅ are
Tan ∅ = opposite / adjacent
= - 3/4 ( given that y = slope which is = Tan ∅ )
now we will find the hypothenuse ( c )
c^2 = a^2 + b^2 = 9 + 16 = 25
therefore ; c = √25 = 5
hence the trig functions are :
sin ∅ = -3/5
cos ∅ =4/5
sec ∅ = 5/4
cosec ∅ = -5/3
cot ∅ = -4/3
Given the function of f(x)=e^xsinx at x = 0.5 and h = 0.25 What is the derivative of the given function using forward finite difference O(h)? a. 0.61036 b. 1.61036 c. 2.61036 d. 3.61036
Answers
The derivative of the given function using forward finite difference O(h) is approximately 0.61036.
To find the derivative of the function f(x) = e^xsinx at x = 0.5 using forward finite difference O(h), we can use the following formula:
f'(x) ≈ (f(x + h) - f(x)) / h
Given that h = 0.25, we can substitute the values into the formula:
f'(0.5) ≈ (f(0.5 + 0.25) - f(0.5)) / 0.25
Next, we need to evaluate the function at the given values:
\(f(0.5) = e^(^0^.^5^)sin(0.5)\)
f(0.5 + 0.25) = e^(0.75)sin(0.75)
Now we can substitute these values into the formula:
f'(0.5) ≈ \((e^(^0^.^7^5^)sin(0.75)\) - \(e^(^0^.^5^)sin(0.5)\)) / 0.25
Using a calculator or numerical methods, we can evaluate this expression and obtain the approximate value of the derivative as 0.61036.
Learn more about Derivative
brainly.com/question/32963989
#SPJ11