Solve the following one-step equations using inverse operations.
1) X + 6 = 13
X =
2) Y - 5 = 22
Y =
3) 8M = -72
M =
4)
E =
Simplify the following problems by combining like terms.
5) 5x + 9 - 2x - 7 =
Simplify the following problem by using the Distributive Property.
6) -5(x + 8) =
Simplify the following problem by Factoring.
7) 10w - 20 =
Answers
2.) 27
3.) -9
5.)
Related Questions
I NEED HELP ASAP!!!!!!!

Answers
Answer:
9/25 = 36%
Step-by-step explanation:
First add up all of the students (150)
Then divide 54 by 150, 0.36
0.36 = 36% = 9/25
What is the name of the segment inside the large triangle?
1. Perpendicular bisector
2.Midsegment
3.Angle Bisector
4.Median

Answers
The name of the segment inside the large triangle is called the: 3. angle bisector.
What is an Angle Bisector?The word "bisect" means to divide into two equal halves. Therefore, an angle bisector can be defined as a line segment that divides the an angle in a triangle into two parts that are of the same angle measure.
The image shows a triangle which has a segment that divides a vertex angle into equal parts. Thus, the segment can be named as an angle bisector.
A perpendicular bisector divides a segment into two equal halves at right angle, while a midsegment joins the middle points of two sides of a triangle. The median also, is a segment that joins a vertex of a triangle to the midpoint of the side that is opposite the angle.
Therefore, we can state that the name of the segment is: 3. angle bisector.
Learn more about the angle bisector on:
https://brainly.com/question/24334771
#SPJ1
Joyce was given a fixed amount of pocket money each month. In January, she spent $100 and saved the rest. In Febuary, she spent 10% less and her saving increased by 25%. How much was Joyce's pocket money for each month.
Answers
Answer:
40
Step-by-step explanation:
By spending10% less ,she saved $10,which was equal to 25%
Joyce's pocket money for each month is $140.
What is a percentage?A ratio or value that may be stated as a fraction of 100 is called a percentage. And it is represented by the symbol '%'.
Given:
Joyce was given a fixed amount of pocket money each month.
In January, she spent $100 and saved the rest.
In February, she spent 10% less,
Spent = 10% of $100 = $10
And her saving increased by 25%.
Savings : 25% = $10
100% = $40
Total : $100 + $40 = $140
Therefore, the total money is $140.
To learn more about the percentage;
https://brainly.com/question/24159063
#SPJ2
Euler method in Matlab
30. Solve: Nxy - 0.5ye-0.1x for osx54 with y(0) = 6.5 dx Plot the solution. =
Answers
The differential equation to be solved is Nxy - 0.5ye-0.1x for osx54 with y(0) = 6.5 dx. This can be solved using Euler's method in MATLAB.
Follow the steps below.
Step 1: Create a function file - The differential equation needs to be defined in a function file first. Let's create a function file named "odefun.m".function dydx = odefun(x,y)
dydx = N*x*y - 0.5*y*exp(-0.1*x);
where N is a constant value that needs to be defined.
Step 2: Define the given values - Define the given values such as N, initial value y(0), and step size dx.
N = ...; %
Define N herey 0 = 6.5; %
Define initial value of y here. dx = ...; %
Define step size here
Step 3: Use Euler's method to solve the differential equation - Now, use Euler's method to solve the differential equation using a for loop. The MATLAB code is as follows: x = 0:dx:54; %
Define range of x values here y = zeros(size(x)); %
Initialize y as a vector of zeros y(1) = y0; %
Assign initial value of y to y(1) for i = 1: length(x)-1 dydx = odefun(x(i),y(i)); y(i+1) = y(i) + dydx*dx; end
Step 4: Plot the solution - Finally, plot the solution using the MATLAB command plot(x,y).
The complete MATLAB code is given below:
N = ...; %
Define N here y0 = 6.5; %
Define initial value of y here dx = ...; %
Define step size here x = 0:dx:54; %
Define range of x values here y = zeros(size(x)); % Initialize y as a vector of zeros y(1) = y0; %
Assign initial value of y to y(1) for i = 1: length(x)-1 dydx = odefun(x(i),y(i)); y(i+1) = y(i) + dydx*dx; end plot(x,y)
The plot of the solution will be displayed.
Learn more about differential equation visit:
brainly.com/question/32645495
#SPJ11
felicia went out to dinner with friends. when the check came, she said she would pay the tip. the tip was 10 percent of the total bill for all 4 people was $22.00. what was the total tip she paid?
Answers
Answer:
$2.20
Step-by-step explanation:
The tip is 10% of $22, or 0.1 * 22 = 2.2
So $2.20 (we can add a hidden 0 on the end)
The length of three sides of a triangle are 3x + 12, 2x +14, and x +12.
6x+5/4
6x+3/4
5x+5/4
5+5/4
Answers
Answer:
6x+5/4
Step-by-step explanation:
Pythagoras
Round the answer to 1 decimal place
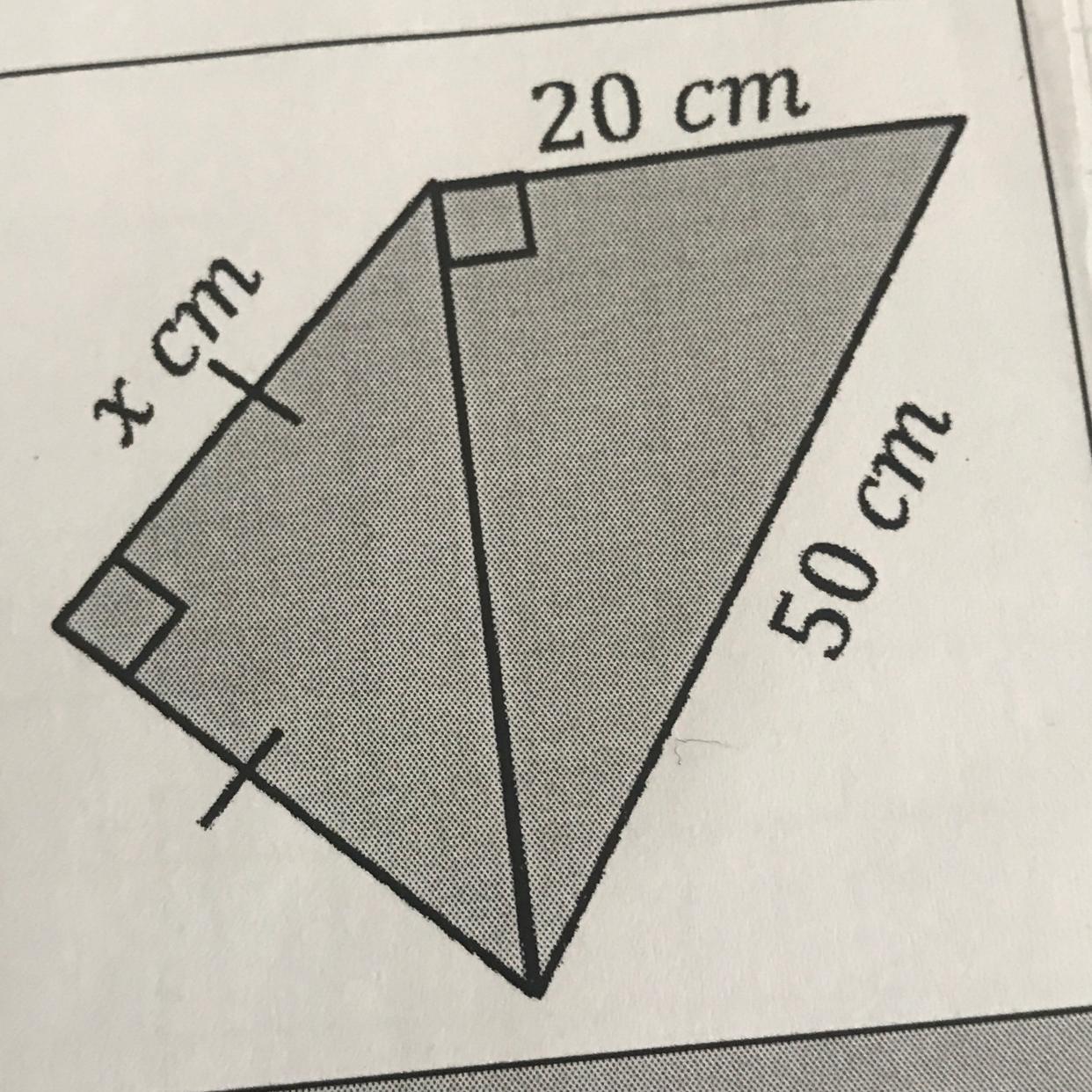
Answers
Answer:
To one decimal place, x = 32.4 cm
Step-by-step explanation:
We can find x by first finding the middle length using the triangle on the right,
let the middle length be c
for the triangle on the right,
hypotenuse = 50 cm
base = 20 cm
Using the Pythagorean theorem,
\((hypotenuse)^2=(base)^2+(height)^2\)
Putting values, we get,
\(50^2 = 20^2+c^2\\c^2 = 50^2-20^2\\c^2=2500-400\\c^2=2100\\c=10\sqrt{21}\)
so, c = 10(sqrt(21))
For the triangle on the left
Now,
For the triangle on the left, the middle length is the hypotenuse,
and we see that both the base and the height are equal (from the small dashes on these sides). i.e base = height = x
So, applying the theorem, we get,
\(c^2 = x^2+x^2\\c^2=2x^2\\(10\sqrt{21})^2=2x^2\\ 2100=2x^2\\2100/2=x^2\\1050 = x^2\\x= 5\sqrt{42}\)
Now, to 1 decimal place, x is,
x = 32.4 cm
katherine gives piano lessons for $15 per hour. she also grows flowers, which she arranges and sells at the local farmer’s one day she spends 5 hours planting $50 worth of seeds in her garden. once the seeds have grown into flowers, she can sell them for $150 at the farmer’s market. katherine’s accounting profits are
Answers
Katherine will make a profit of $100.
To calculate the profit, we need to calculate the total revenue and the total cost. The total cost includes the cost of growing flowers, and the total revenue includes the amount from selling the flowers as well as the money made from piano lessons.The total cost is given by the sum of the cost of planting seeds and growing flowers.
Cost of planting seeds = $50
Total hours spent in planting seeds = 5
Cost of growing flowers = 0 (because the problem doesn’t state how much it costs to grow flowers)
Total Cost = Cost of planting seeds = $50
Total Revenue:The total revenue is given by the sum of the money earned from selling the flowers and the money earned from giving piano lessons.
Money earned from selling flowers = $150
Money earned from piano lessons = 0 (because it is not mentioned in the problem)
Total Revenue = Money earned from selling flowers = $150
Profit:Total profit is given by the difference between total revenue and total cost.
Profit = Total Revenue - Total Cost = $150 - $50 = $100
Therefore, A profit of $100 is made by Katherine.
To know more about profit: https://brainly.com/question/1078746
#SPJ11
Can anyone answer this for me?

Answers
Answer:
y = 2 - \(x^{2}\)
Step-by-step explanation:
\(x^{2}\) results in a parabola (U-shape). Adding a negative in front of it flips the parabola to look like an upside-down U.
The 2 makes it shift up two decimal spots to (0,2).
Let f(x,y) = e2cosy. Find the quadratic Taylor polynomial about (0,0). = + . 8 8 5. Let f(x, y) = xy + Find all of the critical points off and classify each of the critical point of f as 2 y? local maxima, local minima, saddle points, or neither.
Answers
Let f(x,y) = e2cosy. Find the quadratic Taylor polynomial about (0,0). = + . 8 8 5. Let f(x, y) = xy. for the function f(x, y) = xy, the critical point is (0, 0), and it is classified as a saddle point.
To find the quadratic Taylor polynomial about (0,0) for the function f(x, y) = e^(2cos(y)), we need to find the first and second partial derivatives of the function at (0,0).
The first partial derivatives are:
∂f/∂x = 0
∂f/∂y = -2e^(2cos(y))sin(y)
The second partial derivatives are:
∂²f/∂x² = 0
∂²f/∂y² = -4e^(2cos(y))sin(y) - 4e^(2cos(y))cos²(y)
The mixed partial derivative is:
∂²f/∂x∂y = 4e^(2cos(y))sin(y)cos(y)
To obtain the quadratic Taylor polynomial, we evaluate the function and its derivatives at (0,0) and plug them into the general quadratic polynomial equation:
P(x, y) = f(0, 0) + ∂f/∂x(0, 0)x + ∂f/∂y(0, 0)y + 1/2 * ∂²f/∂x²(0, 0)x² + ∂²f/∂y²(0, 0)y² + ∂²f/∂x∂y(0, 0)xy
Plugging in the values, we get:
P(x, y) = 1 + 0x + 0y + 0x² - 4y² + 0xy
Simplifying, we have:
P(x, y) = 1 - 4y²
Therefore, the quadratic Taylor polynomial about (0,0) for the function f(x, y) = e^(2cos(y)) is P(x, y) = 1 - 4y².
For the function f(x, y) = xy, to find the critical points, we need to set both partial derivatives equal to zero:
∂f/∂x = y = 0
∂f/∂y = x = 0
From the first equation, y = 0, and from the second equation, x = 0. Thus, the only critical point is (0, 0).
To classify the critical point, we can use the second partial derivative test. However, since we only have one critical point, the test cannot be applied. In this case, we need to examine the behavior of the function around the critical point.
Considering the function f(x, y) = xy, we can see that it takes the value of zero at the critical point (0, 0). However, there is no clear trend of local maxima or minima in the vicinity of this point. As a result, we classify the critical point (0, 0) as a saddle point.
In summary, for the function f(x, y) = xy, the critical point is (0, 0), and it is classified as a saddle point.
Learn more about Taylor polynomial here:
https://brainly.com/question/32073784
#SPJ11
A bag holds 12 red marbles, 11 green
marbles, 17 blue marbles, and 5 yellow
marbles. What is the probability that
you will NOT choose a blue marble?
5
A
45
(В)
11
45
12
© 45
28
45
Answers
Answer:
62.22%
Step-by-step explanation:
First, find how many total marbles there are:
12 + 11 + 17 + 5
= 45
Then, find how many marbles that are not blue:
12 + 11 + 5
= 28
Then, divide 28 by 45, and multiply by 100
(28/45) x 100
= 62.22% is the probability of not choosing a blue marble
Y=yes
T=total
The Bakhshali Manuscript shows that another method for calculating nonperfect squares was being used in India by 400 CE. Use this method to find the approximate value of. The nearest perfect square that is less than 22 is , whose square root is. Add the square root from step 1 to to get 4. 75. Calculate the quantity one-half times the square of divided by the value found in step 2, or 4. 75. Subtract the value found in step 3 from the value found in step 2, or 4. 75. The approximate value of is.
Answers
The Bakhshali Manuscript reveals an alternate method for calculating nonperfect squares used in ancient India around 400 CE. To find the approximate value of a nonperfect square, we can follow these steps:
The Bakhshali Manuscript provides insights into ancient Indian mathematical techniques, including a method for calculating nonperfect squares. To illustrate this method, let's consider finding the approximate value of a nonperfect square.
First, we need to identify the nearest perfect square that is smaller than the given number. In this case, the nearest perfect square less than 22 is 16, whose square root is 4.
Next, we add the square root obtained in the previous step (4) to the given number (22). This gives us 26.
Then, we calculate one-half times the square of the given number (22) and divide it by the value obtained in the previous step (26). This results in 4.75.
Finally, we subtract the value obtained in the previous step (4.75) from the value obtained in step two (26). The result is approximately 21.25. Therefore, the approximate value of the nonperfect square is 21.25.
This method, found in the Bakhshali Manuscript, provides an ancient technique for estimating the values of nonperfect squares in India during the 4th century CE.
Learn more about square root here: https://brainly.com/question/29286039
#SPJ11
The temperature that milk is pasteurised to kill off most germs:
Answers
Answer:
160 degrees Fahrenheit for 15 seconds
Step-by-step explanation:
Conventionally, milk is pasteurized, or heated at high temperatures to kill harmful germs, at roughly 160 degrees Fahrenheit for 15 seconds. While pasteurization kills most germs, it does not wipe out bacterial spores, the dormant versions of the germs, which are extremely resistant to any form of destruction.
Answer:
160⁰ and 15 minutes can the germs canbe die and the milk can be so clean
A remote control truck at a constant rate of 108 feet in 6 seconds
Answers
Answer:
idk if this is what you wanted or not, but I will tell you the feet per second, because that is what it sounds like you want: The truck travels 18 feet every second
Step-by-step explanation:
all you have to do is divide 108 by 6, and the answer is 18 equation:
108 / 6= 18
PLEASE HELP. it is in the attachment

Answers
Answer:
<JKL=123
Step-by-step explanation:
57+57=114
360-114=246
246/2=123
<JKL=123
Answer:
angle JKL=123 degrees
Step-by-step explanation:
since sides of a rhombus are parallel, angle JKL is supplementary to angle KJM (or same side interior) so angle JKL is 180-57=123 degrees
Determine whether the graphs of y=-2x-7 and -y=2x=13 are parallel, perpendicular, coincident, or none of these.
Answers
Answer:
Step-by-step explanation:
y = -2x - 7
-y = 2x - 13
y = -2x + 13
parallel
pls pls pls pls help me istg ill be your best friend and give you brianliest and all the points i can give and ill love you forvever pls pls pls pls

Answers
a. The chart did not maintain consistent scaling
b. The graph is not the appropriate graph type to display such data
c. The display had inaccurate or distorted visual representations
How do we explain?When the actual data may not support it, changing the scales on the axes might give the appearance of big changes or differences.
The visual effect of data can be exaggerated or minimized, for instance, by adopting a non-linear scale or deleting specific sections of the axis.
So it important to Choose appropriate graph type that best represents the data and the relationship you want to convey.
It also advisable to make use of clear and accurate labeling with descriptive titles and units of measurement.
Learn more about graphs at:
https://brainly.com/question/19040584
#SPJ1
A confectionery company mixes three types of toffees to form one kilogram " toffee packs. the pack is sold at rs. 17. the three types of toffees cost rs.20, rs. 10, rs. 5 per kg. resp. the mixture must contain atleast 300 gms of first type. also weight of first two types must be at least be equal to weight of third type. find the optimal mix for maximum profit.answer
Answers
The maximum profit is 6 and it is obtained when we mix 0.6 kg of type A, 0 kg of type B, and 0.4 kg of type C.
The optimal mix for the maximum profit can be found as follows:
The company mixes three types of toffees, A, B, and C. Let the weights of type A, B, and C be a, b, and c kg, respectively. Let us assume that we are making 1kg of toffee pack. Therefore, the weight of type C should be 1 - (a + b) kg. Also, the mixture must contain at least 300 gms of type A i.e a >= 0.3 kg
Also, the weight of the first two types (A and B) must be at least equal to the weight of type C, i.e a + b >= c. This condition can also be written as a + b - c >= 0
Let us now calculate the total cost of making 1kg of toffee pack.
Cost = 20a + 10b + 5c
If the pack is sold at Rs. 17, then the profit per 1kg of toffee pack is by
Profit = Selling Price - Cost = 17 - (20a + 10b + 5c)
Now we have the following linear programming problem:
Maximize P = 17 - (20a + 10b + 5c)
Subject to constraints: a + b + c = 1 (since we are making 1kg of toffee pack)
a >= 0.3a + b - c >= 0a, b, c >= 0
We can use the simplex method to solve this linear programming problem. However, to save time, we can solve it graphically. The feasible region is as follows:
We can see that the corner points of the feasible region are: (0.3, 0, 0.7), (0.6, 0, 0.4), (0, 0.5, 0.5), and (0, 1, 0).
Let us calculate the profit at each of these corner points. For example, at the point (0.3, 0, 0.7), we have a = 0.3, b = 0, and c = 0.7. Therefore, the profit is
P = 17 - (20(0.3) + 10(0) + 5(0.7)) = 3.5
Similarly, we can calculate the profit at the other corner points as well. The corner point (0.3, 0, 0.7) gives a profit of 3.5
Corner point (0.6, 0, 0.4) result in a profit of 6
Corner point (0, 0.5, 0.5) results in a profit of 5
Corner point (0, 1, 0) gives a profit of 3
You can learn more about optimal mix at: brainly.com/question/30629565
#SPJ11
solve the equation 14m-7m=-56
Answers
Answer:
m=-8
Step-by-step explanation:
14m-7m=-56
7m=-56
m=-8
i think... :)
Answer:
m=-8
Step-by-step explanation:
14m-7m= -56 -----> Combine like terms
7m=-56 ------> Divide -56 by 7
m= -8
Please I need help with questions 8,9,10 and 13 ASAP is due tomorrow

Answers
I HOPE IT WILL HELP YOU.
Thank you.
^ - ^
Sorry if it is wrong.


12) A new amusement park decides to offer its visitors a choice between two plans. With Plan 1 they pay $6 to enter
the park and they pay $3.50 for each ride. With Plan 2 they pay $12 to enter the park and $1.50 for each ride. Write an
equation then find the number of rides when the cost will be the same. What will that cost be?
Answers
Answer:
I don't really understand the question and what they're wanting so sorry
Step-by-step explanation:
Which triangle correctly shows that the side opposite the larger angle is the larger side?
A triangle has side lengths of 13, 5, 10 and angle measures of 30 degrees, 100 degrees, and 50 degrees.
A triangle has side lengths of 5, 5, 5 and angle measures of 60 degrees, 60 degrees, 60 degrees.
A triangle has side lengths 5, 13, 12 and angle measures of 90 degrees, 67 degrees, 23 degrees.
Answers
Answer:
It's the third one for edgen2020!
Step-by-step explanation:
Answer:
it's the third one
Step-by-step explanation:
I just took the test on edg2020 and got it right. I hope this helps you guys.
The cost of a diamond varies as the square of its weight. A diamond weighing 20 decigrams costs Rs. 4,800. Find the cost of a diamond of the same kind weighing 8 decigrams.
Answers
Answer:
768
Step-by-step explanation:
let C represent cost and w weight, then the equation relating them is
C = kw² ← k is the constant of variation
To find k use the condition w = 20, C = 4800, that is
4800 = k × 20² = 400k ( divide both sides by 400 )
12 = k
C = 12w² ← equation of variation
When w = 8, then
C = 12 × 8² = 12 × 64 = 768
after creating a ratio table if each ratio was simplified will you get the same answer for each?plz help 30 points
Answers
Answer:
no that is just impossible to get the same for each
Step-by-step explanation:
Write True and false
A test statistic based on point estimation is used to construct the decision rule which defines the rejection region.
Answers
The given statement is False. A test statistic based on point estimation is not used to construct the decision rule which defines the rejection region.
In hypothesis testing, a test statistic is calculated using sample data and a specific hypothesis to assess the strength of evidence against the null hypothesis. The decision rule, which determines whether to reject or fail to reject the null hypothesis, is based on the test statistic's distribution under the null hypothesis, rather than the point estimate itself.
The construction of the decision rule involves selecting a significance level (alpha), which represents the probability of rejecting the null hypothesis when it is actually true. The rejection region is determined based on the chosen significance level and the distribution of the test statistic. If the calculated test statistic falls within the rejection region, the null hypothesis is rejected; otherwise, it is not rejected.
Point estimation, on the other hand, is used to estimate an unknown parameter of interest, such as the population mean or proportion, based on sample data. It involves calculating a single value (point estimate) that represents the best guess for the parameter value. The point estimate is not directly involved in constructing the decision rule or defining the rejection region in hypothesis testing.
Learn more about test statistic here:
https://brainly.com/question/31746962
#SPJ11
False. A test statistic based on point estimation is not used to construct the decision rule that defines the rejection region.
The process of hypothesis testing involves constructing a decision rule to determine whether to accept or reject a null hypothesis based on sample data. The decision rule is typically defined using a critical region or rejection region, which is a range of values for the test statistic.
Point estimation, on the other hand, is a method used to estimate an unknown population parameter based on sample data. It involves calculating a single value (point estimate) that serves as an estimate of the population parameter.
While point estimation and hypothesis testing are both important concepts in statistics, they serve different purposes. Point estimation is used to estimate population parameters, whereas hypothesis testing involves making decisions based on sample data.
The decision rule for hypothesis testing is typically constructed based on the significance level (alpha) and the distribution of the test statistic, such as the t-distribution or the standard normal distribution. The test statistic is calculated using sample data and compared to critical values or calculated p-values to determine whether to reject the null hypothesis.
Therefore, the statement that a test statistic based on point estimation is used to construct the decision rule defining the rejection region is false.
Learn more about statistic here:
https://brainly.com/question/32201536
#SPJ11
x - y = 2x + 4y = -3
Answers
Step 1:
Write the two equations
x - y = 2 Equation 1
x + 4y = -3 Equation 2
Step 2:
From equation 1 , make x subject of the formula and substitute in equation 2.
\(\begin{gathered} \text{From 1} \\ \text{x - y = 2} \\ \text{x = 2 + y} \end{gathered}\)Step 3:
Substitute x = 2 + y in equation 2
\(\begin{gathered} In\text{ equation 2} \\ x\text{ + 4y = -3} \\ 2\text{ + y + 4y = -3} \\ 5y\text{ = -3 - 2} \\ \text{5y = -5} \\ y\text{ = }\frac{-5}{5} \\ \text{y = -1} \end{gathered}\)Step 4
Substitute y = -1 in x = 2 + y to find x
x = 2 - 1
x = 1
Final answer
x = 1 , y = -1
Equation: x - y = 2x + 4y = -3 x - y = -3 Equations 1st and 2 (x - y = -3) 2 equations 1 2x - 2y = -6 equation 1 -(2x + 4y = -3) equation 2 are obtained.
In the second equation, 2x - 2y = -6, 2x -4y = 3, 6y = 3, and 6y = -3/-6 = 1/2.
2x + 4y = -3 , 2x + 4×1/2 = -3
2x +2 = -3 , 2x = -3 -2 , 2x = -5 ,x = -5/2
The last solution is y = 1/2 and x = -5/2.
What you want altered should go here. After that, click the button below. It's that simple!
Find all cube roots of the complex number in the image provided. Workout out the problem and leave the answers in polar form.

Answers
Given the complex number:
\(z=r\cdot(\cos \theta+i\cdot\sin \theta)\text{.}\)The n n-th roots of the complex number z are given by:
\(w_k=\sqrt[n]{r}\cdot\lbrack\cos (\frac{\theta+k\cdot360\degree}{n})+i\cdot\sin (\frac{\theta+k\cdot360\degree}{n})\rbrack\text{ where }k=0,1,2,\ldots,n-1.\)We must find all the cube roots of the following complex number:
\(z=64\cdot(\cos (219\degree)+i\cdot\sin (219\degree)).\)For this number, we identify:
\(\begin{gathered} r=64, \\ \theta=219\degree. \end{gathered}\)Using the formula above with these numbers, we get:
\(\begin{gathered} w_0=\sqrt[3]{64}\cdot\lbrack\cos (\frac{219\degree+0\cdot360\degree}{3})+i\cdot\sin (\frac{219\degree+0\cdot360\degree}{3})\rbrack=4\cdot\lbrack\cos (73\degree)+i\cdot\sin (73\degree)\rbrack, \\ w_1=\sqrt[3]{64}\cdot\lbrack\cos (\frac{219\degree+1\cdot360\degree}{3})+i\cdot\sin (\frac{219\degree+1\cdot360\degree}{3})\rbrack=4\cdot\lbrack\cos (193\degree)+i\cdot\sin (193\degree)\rbrack, \\ w_2=\sqrt[3]{64}\cdot\lbrack\cos (\frac{219\degree+2\cdot360\degree}{3})+i\cdot\sin (\frac{219\degree+2\cdot360\degree}{3})\rbrack=4\cdot\lbrack\cos (313\degree)+i\cdot\sin (313\degree)\rbrack\text{.} \end{gathered}\)Answer
\(\begin{gathered} w_0=4\cdot\lbrack\cos (73\degree)+i\cdot\sin (73\degree)\rbrack \\ w_1=4\cdot\lbrack\cos (193\degree)+i\cdot\sin (193\degree)\rbrack \\ w_2=4\cdot\lbrack\cos (313\degree)+i\cdot\sin (313\degree)\rbrack \end{gathered}\)The quadratic formula can be used to solve any quadratic equation in standard form.
True or False
Answers
Answer:
True
Step-by-step explanation:
The quadratic formula can be applied to any quadratic equation in the form \(ax^2+bx+c=0\) (standard form).
The quadratic formula: \(\displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
I hope this helps!
Answer:
its true
Step-by-step explanation:

Rewrite x(t)=(1.45)^t/2 in the form y=a(1+r)^t or y=a(1-r)^t to determine whether it represents exponential growth or exponential decay. Round a and r to the nearest hundredth if necessary.
Answers
The given function represents exponential growth, the value of a is 1 and the value of r is 0.45.
What is the exponential growth?The quantity increases slowly after which the rate of change and the rate of growth increases over a period of time rapidly. This increase in growth is calculated by using the exponential growth formula.
The exponential growth formula is \(Amount = Initial value(1+\frac{r}{100} )^{\frac{t}{n}}\).
The given exponential function is \(x(t)=(1.45)^{\frac{t}{2} }\).
Now, \(x(t)=(1+0.45)^{\frac{t}{2} }\)
Compare, \(x(t)=(1+0.45)^{\frac{t}{2} }\) with \(y=a(1+r)^t\), we get
a=1 and r=0.45
Therefore, the value of a is 1 and the value of r is 0.45.
Learn more about the exponential growth and decay here:
https://brainly.com/question/13674608.
#SPJ9
brainiest help and points !!!! Point A has coordinates (4,2). The x-coordinate of point B is 13. The distance between point A and point B is 15 units. Your friend says the coordinates of point B could be (16,11). What are the possible coordinates of point B? What mistake did your friend make? The possible coordinates of point B are nothing. (Type an ordered pair. Use a comma to separate answers as needed.) What mistake did your friend make? A. Your friend switched the hypotenuse length for one of the leg lengths. B. Your friend used the given distance as one of the leg lengths instead of the hypotenuse length. C. Your friend's point does not have the same x-coordinate as point B. Your friend switched the leg lengths of the right triangle. D. Your friend moved the correct distance but the incorrect direction on the coordinate plane.
Answers
Answer:
B. Your friend used the given distance as one of the leg lengths instead of the hypotenuse length.