Solve the system of linear equations.
y=−2x−4
y=2x−4
(−1, 2)
(2, 2)
(−2, 0)
(3, 7)
(0,−4)
(7, 7)
(0, 4)
no solution
(1, 1)
infinitely many solutions
Answers
Answer:
Infinitely many solutions.
Step-by-step explanation:
(Y= -2x-4) (y=2x-4)
-2x - 4 = 2x - 4
-2x + 2x = -4 + 4
0 = 0
Related Questions
What is the area of this tile? in. in? 4 in. I in.

Answers
Answer:
1*4 = 4 in^2
Step-by-step explanation:
The area for this shape is calculated by multiplying width and length:
1*4 = 4 in^2
the rotational speed of a driven gear is inversely proportional to the number of teeth on a gear. you are replacing a gear having 200 teeth with one that has 50 teeth and turns 2,000 rpm. what was the rpm of the gear having 200 teeth?
Answers
The revolution of the gear having 200 teeth was 500 rpm.
What is Ratio?The ratio is defined as a relationship between two quantities, it is expressed as one divided by the other.
Given that the rotational speed of a driven gear is inversely proportional to the number of teeth on a gear.
T1/T2 = R2/R1
As per the question, the required values as
T1 = 200
T2 = 50
R2 = 2,000 rpm
200/50 = 2,000 /R1
R1 = (2,000 × 50)/200
R1 = 500
Therefore, the revolution of the gear having 200 teeth was 500 rpm.
Learn more about the Ratio here:
brainly.com/question/1504221
#SPJ1
need help understanding

Answers
Answer:
you need to write a problem with it
Step-by-step explanation:
for example,
Q4 will be 9n
n is the unknown number
9 is what n will be multiplyed with
multiplied since product means answer of a multiplication problem
hoped this helps
Drag the tiles to the boxes to form correct pairs. Not all tiles will be used. Match the circle equations in general form with their corresponding equations in standard form. x2 + y2 − 4x + 12y − 20 = 0
(x − 6)2 + (y − 4)2 = 56
x2 + y2 + 6x − 8y − 10 = 0
(x − 2)2 + (y + 6)2 = 60
3x2 + 3y2 + 12x + 18y − 15 = 0
(x + 2)2 + (y + 3)2 = 18
5x2 + 5y2 − 10x + 20y − 30 = 0
(x + 1)2 + (y − 6)2 = 46
2x2 + 2y2 − 24x − 16y − 8 = 0
x2 + y2 + 2x − 12y − 9 = 0
Answers
Answer:
1) For \(x^2 + y^2 - 4x + 12y - 20 = 0\), the standard form is \((x-2)^2 + (y+6)^2 = 60\\\)
2) For \(x^2 + y^2 + 6x - 8y - 10 = 0\), the standard form is \((x + 3)^2 + (y - 4)^2 = 35\\\)
3) For \(3x^2 + 3y^2 + 12x + 18y - 15 = 0\), the standard form is \((x + 2)^2 + (y+ 3)^2 = 18\\\)
4) For \(5x^2 + 5y^2 - 10x + 20y - 30 = 0\), the standard form is \((x - 1)^2 + (y+ 2)^2 = 11\\\)
5) For \(2x^2 + 2y^2 - 24x - 16y - 8 = 0\), the standard form is \((x - 6)^2 + (y+ 4)^2 = 56\\\)
6) For\(x^2 + y^2 + 2x - 12y - 9 = 0\), the standard form is \((x+1)^2 + (y-6)^2 = 46\\\\\)
Step-by-step explanation:
This can be done using the completing the square method.
The standard equation of a circle is given by \((x - a)^2 + (y-b)^2 = r^2\)
1) For \(x^2 + y^2 - 4x + 12y - 20 = 0\)
\(x^2 - 4x + y^2 + 12y = 20\\x^2 - 4x + 2^2 + y^2 + 12y + 6^2 = 20 + 4 + 36\\(x-2)^2 + (y+6)^2 = 60\\\)
Therefore, for \(x^2 + y^2 - 4x + 12y - 20 = 0\), the standard form is \((x-2)^2 + (y+6)^2 = 60\\\)
2) For \(x^2 + y^2 + 6x - 8y - 10 = 0\)
\(x^2 + 6x + y^2 - 8y = 10\\x^2 + 6x + 3^2 + y^2 - 8y + 4^2 = 10 + 9 + 16\\(x + 3)^2 + (y- 4)^2 = 35\\\)
Therefore, for \(x^2 + y^2 + 6x - 8y - 10 = 0\), the standard form is \((x + 3)^2 + (y - 4)^2 = 35\\\)
3) For \(3x^2 + 3y^2 + 12x + 18y - 15 = 0\)
Divide through by 3
\(x^2 + y^2 + 4x + 6y = 5\)
\(x^2 + y^2 + 4x + 6y = 5\\x^2 + 4x + 2^2 + y^2 + 6y + 3^2 = 5 + 4 + 9\\(x + 2)^2 + (y+ 3)^2 = 18\\\)
Therefore, for \(3x^2 + 3y^2 + 12x + 18y - 15 = 0\), the standard form is \((x + 2)^2 + (y+ 3)^2 = 18\\\)
4) For \(5x^2 + 5y^2 - 10x + 20y - 30 = 0\)
Divide through by 5
\(x^2 + y^2 - 2x + 4y = 6\)
\(x^2 + y^2 -2x + 4y = 6\\x^2 - 2x + 1^2 + y^2 + 4y + 2^2 = 6 + 1 + 4\\(x - 1)^2 + (y+ 2)^2 = 11\\\)
Therefore, for \(5x^2 + 5y^2 - 10x + 20y - 30 = 0\), the standard form is \((x - 1)^2 + (y+ 2)^2 = 11\\\)
5) For \(2x^2 + 2y^2 - 24x - 16y - 8 = 0\)
Divide through by 2
\(x^2 + y^2 - 12x - 8y = 4\)
\(x^2 + y^2 - 12x - 8y = 4\\x^2 - 12x + 6^2 + y^2 - 8y + 4^2 = 4 + 36 + 16\\(x - 6)^2 + (y+ 4)^2 = 56\\\)
Therefore, for \(2x^2 + 2y^2 - 24x - 16y - 8 = 0\), the standard form is \((x - 6)^2 + (y+ 4)^2 = 56\\\)
6) For \(x^2 + y^2 + 2x - 12y - 9 = 0\)
\(x^2 + 2x + y^2 - 12y = 9\\x^2 + 2x + 1^2 + y^2 - 12y + 6^2 = 9 + 1 + 36\\(x+1)^2 + (y-6)^2 = 46\\\)
Therefore, for\(x^2 + y^2 + 2x - 12y - 9 = 0\), the standard form is \((x+1)^2 + (y-6)^2 = 46\\\\\)
For Plato / Edmentum
Just to the test and got it right ✅

Answer and Complete all the problems.
I will mark brainiest.

Answers
Answer:
Answer given below
Step-by-step explanation:
1. A = (0, 5) = on y axis
2. B = (0, -3) = on x axis
3. C = (1, 2) = 1st quadrant
4. D = (-4, -3) = 3rd quadrant
5. E = (5, -5) = 4th quadrant
6. x axis
7. y axis
See the question above.
A) 96 ft2
B) 24 ft2
C) 48 ft2
D) 38 ft2

Answers
Answer:
C. 48 \(ft^2\)
Step-by-step explanation:
The formula for finding the area of a triangle is:
\(\frac{1}{2}bh\)
The "\(b\)," is the base (10), and the "\(h\)," is the height (9.6), so plug it in:
\(\frac{1}{2} (10)(9.6)\\\)
\(\frac{1}{2} (96)\)
48 \(ft^2\)
I need help again! :)

Answers
Answer:
Fraction: x= 4/5
Decimal: x= 0.8
The probability of selecting a T or a P on the second draw, given that an F was selected on the first draw is
Answers
The probability of selecting a T or a P on the second draw, given that an F was selected on the first draw is 0.39.
What is probability?The probability of selecting a T or a P on the second draw, given that an F was selected on the first draw, can be calculated using conditional probability.
P(A|B) = P(A and B) / P(B)
P(A and B) = P(T or P on second draw and F on first draw) = P(T on second draw and F on first draw) + P(P on second draw and F on first draw)
= (3/9) x (4/10) + (2/9) x (4/10) = 14/90
To find P(B), we know that it is 0.4.
Therefore, the conditional probability of selecting a T or a P on the second draw, given that an F was selected on the first draw, is:
P(A|B) = P(A and B) / P(B) = (14/90) / 0.4 ≈ 0.39
So the probability of selecting a T or a P on the second draw, given that an F was selected on the first draw, is approximately 0.39.
Learn more about probability, here:
https://brainly.com/question/30034780
#SPJ1
Which statement about the value of x is true? x > 38 x < 39 x < 77 x > 103
Answers
Answer:
The correct answer is x>38
Step-by-step explanation:
The solution is : x = 77 and x > 38
What is an angle?In Plane Geometry, a figure which is formed by two rays or lines that shares a common endpoint is called an angle. The two rays are called the sides of an angle, and the common endpoint is called the vertex.
Given that,
Sum of all angles in a triangle is 180.
The angle PNO will hence be:
180 - 38 - 39 = 103 degrees.
The angle PNO + angle x = 180 degrees (straight line)
So 103 + x = 180,
therefore x = 180 - 103 = 77.
Which is also greater than 38,
so, x > 38 is also correct.
Hence the solution is : x = 77 and x > 38
To learn more on angle click:
brainly.com/question/28451077
#SPJ7

True or False.
If a set of vectors {v1, v2, ...., vp} in R^n is linearly dependent, then p>n.
Answers
The statement "If a set of vectors {v₁, v₂, ...., vp} in Rⁿ is linearly dependent, then p>n" is False.
Let {v₁, v₂, ...., vp} be a set of p vectors in Rⁿ, then the following are equivalent statements:
1. The set of vectors is linearly dependent.
2. There exist constants c₁, c₂, ... cp, not all of them zero, such that:
c₁v₁+c₂v₂+...+cpvp = 0 (zero vector)
For the above to be possible, the following must hold true: p≥n
Because in Rⁿ, each vector has n components.
So, the total number of unknowns is p, while the total number of equations that we have is n.
Hence p≥n for the system of linear equations above to have a non-zero solution.
Hence, the statement "If a set of vectors {v₁, v₂, ...., vp} in Rⁿ is linearly dependent, then p>n" is False.
To learn more about set of vectors from the given link.
https://brainly.com/question/15519257
#SPJ11
measuring the entire population is usually preferred over measuring a sample from the population.
T/F
Answers
The given statement "Measuring the entire population is usually preferred over measuring a sample from the population" is False because measuring the entire population is often impractical or impossible.
When dealing with large populations, it is typically more feasible to gather data from a representative sample rather than measuring the entire population. This approach saves time, resources, and effort. Sampling allows statisticians to make reliable inferences about the population based on the characteristics observed in the sample.
Carefully chosen samples can accurately reflect the population's attributes and provide valuable insights.
However, it is crucial to ensure that the sample is representative and unbiased to avoid potential sampling errors and ensure the validity of the conclusions drawn from the data.
For more questions like Population click the link below:
https://brainly.com/question/27779235
#SPJ11
Solve:
\(0=x^{5}+x^{4}-20x^{3}-68x^{2}-80x-32\)
Answers
The solution to the equation is x = -2, -1.46, -1, x = 5.46
How to determine the solution to the equationFrom the question, we have the following parameters that can be used in our computation:
0 = x^{5}+x^{4}-20x^{3}-68x^{2}-80x-32
Express properly
So, we have
x^5 + x^4 - 20x^3 -68x^2 -80x - 32 = 0
Next, we plot the graph of x^5 + x^4 - 20x^3 -68x^2 -80x - 32 = 0 to determine the solution graphically
See attachment for graph
From the graph, we have
x = -2, -1.46, -1, x = 5.46
Read more about equations at
brainly.com/question/2972832
#SPJ1
![Solve: [tex]0=x^{5}+x^{4}-20x^{3}-68x^{2}-80x-32[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/rdMOFg1zczNLSWw93JzNS1sgYUJSEChQ.jpeg)
4. A right triangle has legs with lengths of 6 feet and 9 feet. The hypotenuse of the triangle, in feet,
is between:
A. 4 and 5
B. 6 and 9
C. 9 and 10
D. 10 and 11
E. 11 and 13

Answers
C^2 = A^2 + B^2
C^2 = (6)^2 + (9)^2
C^2 = 36 + 81
C^2 = 117
C = square root of 117
C = About 10.81 feet
So, in conclusion, the hypotenuse or the longest side of the triangle in feet is: D. Between 10 feet and 11 feet.
Answer:
D. 10 and 11
Step-by-step explanation:
This problem would use pythagorean theorem because we're finding the hypotenuse of a right triangle. This is its standard equation:
\(a {}^{2} + {b}^{2} = {c}^{2} \)
The legs represent \(a\) and \(b\) respectively, and \(c\) represents the hypotenuse. After plugging in the legs' respective values, the equation looks like this:
\(6^{2} + {9}^{2} = {c}^{2} →36 + 81 = {c}^{2} →117 = c^{2} \)
To isolate \(c\), you would find the square root of \(117\). In this case, we're just finding which integers\( \sqrt{117} \) is between. \(\sqrt{100}(=10)\) is the closest integer value below \(\sqrt{117}\) and \(\sqrt{121}(=11)\) is the closest integer value above \(\sqrt{117}\). So the answer is D. 10 and 11.
the ratio of peas Julia had to a number of peas Vlada had was 3:2 after Julia gave 15 peas, she still has 10 more peas than Vlada. How many peas did Julia have at first?
Answers
Answer:
Julia had 120 peas to start .
Answer:
120 peas
Step-by-step explanation:
Before Julia gave Vlada 15 peas, the ratio of their numbers was 3:2. Afterward, Julia still had 10 more peas. You want to know the number Julia started with.
SolutionLet j represent the initial number of peas Julia had. Then Vlada had 2/3j peas. After the transfer, the difference was ...
(j -15) -(2/3j +15) = 10
1/3j -30 = 10
1/3j = 40
j = 120
Julia had 120 peas at first.
__
Additional comment
The transfer of peas decreases the difference by 30, so if it remains 10 it must have originally been 40. The difference in initial ratio units is 3-2 = 1, so Julia's initial 3 ratio units represent 3·40 = 120 peas.
<95141404393>
Suppose that A and B are points on the number line.
If AB=5 and B lies at 12, where could A be located?
If there is more than one location, separate them with commas.
:0
Location(s) of A :
0.0....
X

Answers
Answer:
locations of A are 7, 17
Step-by-step explanation:
since B is positioned at 12 and AB = 5 , then
A = 12 - 5 or 12 + 5 = 7 , 17
Having trouble solving this:

Answers
Answer:
3\(\frac{727}{1000}\)
List the whole number factors of 18
Answers
Answer:
3,6, and 9
Step-by-step explanation:
Answer:
1, 2, 3, 6, 9, 18
Step-by-step explanation:
1 x 18
2 x 9
3 x 6
A farmer has 20 boxes of eggs
there are 6 eggs in each box
write as a ratio, the number of eggs in two boxes to the total number of eggs
Give your answer in its simplest form
Answers
Answer:
1 : 10 is the answer.
Step-by-step explanation:
Total number of eggs in 2 boxes = 6 x 2 = 12
Total number of eggs in 20 boxes = 120
12 : 120
1 : 10
Answer:
1:6
Step-by-step explanation:
PLEASE ANSWER TOADAY !!!!!!!!!!!!!!!!!

Answers
Answer:
most likely next spring
Step-by-step explanation:
Step-by-step explanation:
the variance of a sample of 81 observations is 64. calculate the standard deviation. round your answer to two decimals.
Answers
The standard deviation is 8.
What is standard deviation?Data dispersion in regard to the mean is quantified by a standard deviation, or. Data are said to be more closely grouped around the mean when the standard deviation is low and more dispersed when the standard deviation is high. A measure of a group of values' variance or dispersion in statistics is called the standard deviation. The values tend to be close to the set's mean when the standard deviation is low, while the values are dispersed over a larger range when the standard deviation is high. The dispersion of the data around the mean value is measured by the standard deviation. It might be helpful when comparing data sets that may have the same mean but a different range.
To know more about standard deviation ,visit:
brainly.com/question/13905583
#SPJ4
a carpenter is building a rectangular room with a fixed perimeter of 600 feet. what are the dimensions of the largest room that can be built? what is its area? 150 ft by 150 ft; 22,500 ft2 300 ft by 300 ft; 90,000 ft2 60 ft by 540ft; 32,400 ft2 150 ft by 450 ft; 67,500 ft2
Answers
To find the dimensions of the largest room that can be built with a fixed perimeter of 600 feet.
We need to divide the perimeter by 2 and use that as the sum of two adjacent sides. Let's call the length of the rectangle "l" and the width "w".
So we have: 2l + 2w = 600
Simplifying: l + w = 300
We want to maximize the area of the rectangle, which is given by: A = lw
We can solve for one variable in terms of the other: l = 300 - w
Substituting into the area equation:
A = (300 - w)w
A = 300w - w^2
To maximize the area, we need to find the value of w that makes the derivative of A with respect to w equal to 0: dA/dw = 300 - 2w = 0
w = 150
So the width of the rectangle is 150 feet. Substituting back into the perimeter equation: l + 150 = 300
l = 150
So the length of the rectangle is also 150 feet.
Therefore, the largest room that can be built has dimensions 150 ft by 150 ft, and its area is: A = lw = 150 * 150 = 22,500 ft^2
The dimensions of the largest rectangular room a carpenter can build with a fixed perimeter of 600 feet are 150 ft by 150 ft. The area of this room is 22,500 ft². This is because when the length and width are equal, the area of the rectangle is maximized.
To know more about dimensions visit:-
https://brainly.com/question/2346024
#SPJ11
problem 1 (100 points) fig. 1 depicts a sample power system. suppose the three units are always running, with the following characteristics: unit 1: pmin
Answers
The total cost of power generation for a specific load demand can be calculated by optimally allocating the load demand to each unit based on their power output limits. The allocation is done in a way that minimizes the overall cost while meeting the load demand.
In the given power system depicted in Figure 1, there are three units that are always running. Each unit has specific characteristics regarding their minimum power output (Pmin), maximum power output (Pmax), and incremental cost (Ci). Let's discuss the characteristics of each unit and calculate the total cost of power generation for a given load demand.
Unit 1:
Pmin = 200 MW
Pmax = 500 MW
Ci = $50/MWh
Unit 2:
Pmin = 150 MW
Pmax = 400 MW
Ci = $40/MWh
Unit 3:
Pmin = 100 MW
Pmax = 300 MW
Ci = $30/MWh
To calculate the total cost of power generation for a given load demand, we need to determine the optimal power output for each unit. We start by considering the units with the lowest incremental cost first.
Suppose the load demand is D MW. We allocate the load demand to the units as follows:
Step 1: Check if Unit 1 can meet the load demand within its power range. If yes, allocate the load demand to Unit 1 and calculate the cost:
Cost1 = Ci * P1, where P1 is the power output of Unit 1.
Step 2: If there is still remaining load demand, allocate it to Unit 2:
Cost2 = Ci * P2, where P2 is the power output of Unit 2.
Step 3: If there is still remaining load demand, allocate it to Unit 3:
Cost3 = Ci * P3, where P3 is the power output of Unit 3.
Finally, the total cost of power generation, Cost_total, is the sum of Cost1, Cost2, and Cost3:
Cost_total = Cost1 + Cost2 + Cost3
To find the optimal power output for each unit, we consider the load demand and compare it to the minimum and maximum power output limits for each unit. The power allocation is based on meeting the load demand while minimizing the overall cost of power generation.
In summary, given the characteristics of the three units in the power system (Pmin, Pmax, and Ci), the total cost of power generation for a specific load demand can be calculated by optimally allocating the load demand to each unit based on their power output limits. The allocation is done in a way that minimizes the overall cost while meeting the load demand.
Learn more about demand here
https://brainly.com/question/14274996
#SPJ11
(a) Determine the smallest positive value of n for which a simple graph on n vertices and 2n edges can exist. Give an example of such a graph for the smallest n. (b) Let G be a simple graph with 20 vertices. Suppose that G has at most two com- ponents, and every pair of distinct vertices u and v satisfies the inequality that deg(u) + deg(v) > 19. Prove that G is connected.
Answers
(a) The smallest positive value of n for which a simple graph on n vertices and 2n edges can exist is 3. An example of such a graph for the smallest n is a triangle, where each vertex is connected to the other two vertices.
In this case, we have 3 vertices and 2n = 2 * 3 = 6 edges, which satisfies the condition.
To determine the smallest positive value of n, we need to consider the conditions for a simple graph:
1. Each vertex must be connected to at least one other vertex.
2. There should be no multiple edges between the same pair of vertices.
3. There should be no self-loops (edges connecting a vertex to itself).
Considering these conditions, we start by trying with the smallest possible n, which is 3. We construct a graph with 3 vertices and connect each vertex to the other two vertices, resulting in a triangle. This graph satisfies the conditions and has 2n = 2 * 3 = 6 edges.
(b) To prove that G is connected, we will use a proof by contradiction.
Assume that G is not connected, meaning it has two or more components. Let's consider two distinct components, C1 and C2.
Since G has at most two components, each component can have at most 10 vertices (20 vertices / 2 components). Let's assume C1 has x vertices and C2 has y vertices, where x + y ≤ 20.
Now, let's consider two vertices u and v, where u belongs to C1 and v belongs to C2. According to the given condition, deg(u) + deg(v) > 19.
Since deg(u) represents the degree of vertex u, it means the number of edges incident to vertex u. Similarly, deg(v) represents the degree of vertex v.
In C1, the maximum possible degree for a vertex is x - 1 (since there are x vertices, each connected to at most x - 1 other vertices in C1). Similarly, in C2, the maximum possible degree for a vertex is y - 1.
Therefore, deg(u) + deg(v) ≤ (x - 1) + (y - 1) = x + y - 2.
But according to the given condition, deg(u) + deg(v) > 19. This contradicts the assumption that G has at most two components.
Hence, our assumption that G is not connected is false. Therefore, G must be connected.
In conclusion, if a simple graph G has 20 vertices, at most two components, and every pair of distinct vertices satisfies the inequality deg(u) + deg(v) > 19, then G is connected.
To learn more about vertices, click here: brainly.com/question/31767946
#SPJ11
plz help me step by step

Answers
Answer:
x = - 6
Step-by-step explanation:
Equation
1/3 * (-9x +12) = 22 Multiply both sides by 3
Solution
3 * 1/3(-9x + 12) = 22*3
- 9x + 12 = 66 Subtract 12 from both sides.
-9x = 66 - 12 Combine
-9x = 54 Divide by -9
x = 54/-9
x = - 6
andre drew a plan of a courtyard at a scale of 1 to 60. in his drawing, one side of the courtyard is 2.75 inches. what is the actual measurement of that side of the courtyard (in inches)?
Answers
The actual measurement of that side of the courtyard = 165 inches
In this question, we have been given Andre drew a plan of a courtyard at a scale of 1 to 60. in his drawing, one side of the courtyard is 2.75 inches.
We need to find the actual measurement of that side of the courtyard.
In order to calculate the real length,
real length = scale length / scale ratio
here, scale length = 2.75 inches
scale ratio = (1/60)
so, the real length would be,
real length = 2.75/ (1/60)
real length = 2.75 * 60
real length = 165 inches
Therefore, the actual measurement of that side of the courtyard = 165 inches
Learn more about scaling here:
https://brainly.com/question/11349851
#SPJ4
For the linear regression y = ẞ1 + ẞ2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 +681 +382 + 18ẞ1ẞ2
Derive the partial derivatives of SSE with respect to B1 and B2 and solve the optimal values of these parameters.
a. B₁ = B1
b. B₂ =
Answers
The optimal values of these parameters are:
a. β₁ = 0
b. β₂ = 0
The linear regression y = β1 + β2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 + 681 + 382 + 18β1β2
Derive the partial derivatives of SSE with respect to β1 and β2 and solve the optimal values of these parameters.
Given that SSE = 382 + 681 + 382 + 18β1β2 ∂SSE/∂β1 = 0 ∂SSE/∂β2 = 0
Now, we need to find the partial derivative of SSE with respect to β1.
∂SSE/∂β1 = 0 + 0 + 0 + 18β2 ⇒ 18β2 = 0 ⇒ β2 = 0
Therefore, we obtain the optimal value of β2 as 0.
Now, we need to find the partial derivative of SSE with respect to β2. ∂SSE/∂β2 = 0 + 0 + 0 + 18β1 ⇒ 18β1 = 0 ⇒ β1 = 0
Therefore, we obtain the optimal value of β1 as 0. Hence, the partial derivative of SSE with respect to β1 is 18β2 and the partial derivative of SSE with respect to β2 is 18β1.
Thus, the optimal values of β1 and β2 are 0 and 0, respectively.
Therefore, the answers are: a. β₁ = 0 b. β₂ = 0
Learn more about regression analysis at
https://brainly.com/question/31691955
#SPJ11
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!8

Answers
\(\huge \bf༆ Answer ༄\)
The Slope of the line is the rate of change shown in the graph.
Taking two points on the line (1 , 6) and (2 , 12)
Slope (m) is equal to : -
\( \sf \dfrac{y_2 - y_1}{x_2 - x_1} \)\( \sf \dfrac{12 - 6}{2 - 1} \)\( \sf \dfrac{6}{1} \)\( \sf6\)Hence, Rate of change is $6 / hour
\(꧁ \: \large \frak{Eternal \: Being } \: ꧂\)
What is the smallest positive integer that is both a multiple of $7$ and a multiple of $4$?
Answers
The smallest positive integer that is both a multiple of 7 and a multiple of 4, is 28 .
How to find the smallest positive integer ?To find the smallest positive integer that is both a multiple of 7 and a multiple of 4, first find the multiples of both 4 and 7 to see which multiples are common between them and which are the lowest.
The multiples of 4 and 7 are:
Multiples of 4 :
4, 8, 12, 26, 20, 24, 28, 32, 36, 40,
Multiples of 7 :
7 , 14 , 21 , 28 , 35 , 42 , 49
The smallest positive integer that is both a multiple of 7 and a multiple of 4 is therefore 28.
Find out more on multiples at https://brainly.com/question/14312051
#SPJ1
Seriously, somebody please help me! I've been asking all day, someone actually help me and not just halfassly answer it for points.
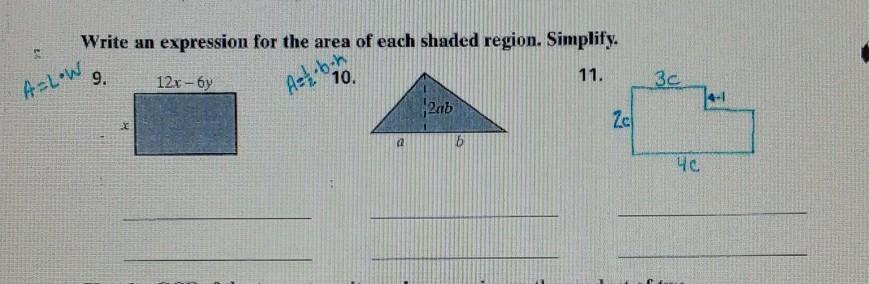
Answers
Answer:
9. A = Length by Width
Length = x
Width = 12x - 6y
A = x(12x - 6y)
A = 12x² - 6xy
10. A = ½bh
h = 2ab
A = ½(b)(2ab)
A = ab²
17/21 + 2/3
please help me.
it's actually confusing for me to understand that the 2 changes to 14, but how?
step by step explanation please.
Answers
Answer:
31/21
Step-by-step explanation:
17/21+2/3
First step is to get both denominators equal so 3 should be multiplied by 7 to get 21 and 2 should also be multiplied by 7,
This leaves 17/21+14/21 which equals to 31/21
Answer:
Step-by-step explanation:
What you want to do is find a common denominator of this equation. You can actually use 21 as that denominator because 7×3=21.
You'll keep the 17/21 for your first value, and for the second...
multiply each side of 2/3 by 7/7. That will end up being 14/21.
Finally, you will add those two values up and get 31/21 or 1 10/21.