Solve the system : { x1+x2-2x3=-1 , 5x1+6x2-4x3=8.
Answers
The solution to the system of equations is x₁ = 3, x₂ = -2, and x3 = 2.
The given system of equations is as follows:
Equation 1: x₁ + x₂ - 2x₃ = -1Equation 2: 5x₁ + 6x₂ - 4x₃= 8To solve this system, we can use the method of elimination or substitution. Let's use the method of elimination to find the values of x₁, x₂, and x₃.
First, we'll eliminate the x₁ term by multiplying Equation 1 by -5 and adding it to Equation 2:
-5(x₁ + x₂ - 2x₃) = -5(-1)-5x₁ - 5x₂ + 10x₃ = 5The new Equation 2 becomes:
-5x₂ + 6x₂ - 4x₃ + 10x₃ = 5 + 8x₂ + 6x₃ = 13Now, let's eliminate the x₂ term by multiplying Equation 1 by 6 and subtracting it from Equation 2:
6(x₁+ x₂ - 2x₃) = 6(-1)6x₁ + 6x₂ - 12x₃ = -6The new Equation 2 becomes:
-5x₁ + 6x₁ - 4x₃ - 12x₃ = 8 - 6x₁ - 16x₃ = 2We now have a system of two equations with two unknowns:
Equation 3: x₂ + 6x₃= 13Equation 4: x₁ - 16x₃ = 2To solve this system, we can solve Equation 4 for x₁:
x₁ = 16x₃ + 2
Now substitute this value of x₁ into Equation 3:
16x₃ + 2 + 6x₃ = 1322x₃ = 11x₃= 11/22x₃ = 1/2Substituting this value of x₃ back into Equation 4:
x₁= 16(1/2) + 2x₁= 8 + 2x₁= 10Finally, substitute the values of x₁ and x₃ into Equation 3:
x₂ + 6(1/2) = 13x₂ + 3 = 13x₂ = 13 - 3x₂ = 10Therefore, the solution to the system of equations is x₁ = 10, x₂ = 10, and x₃ = 1/2.
Learn more about elimination
brainly.com/question/32403760
#SPJ11
Related Questions
The table represents quadratic function g. Which statement is true about the function?
I
-5
-4 -3
-2 -1 0
-1
0
-1
-4 -9 -16
O A. The minimum occurs at the function's x-intercept.
O B.
The maximum occurs at the function's x-intercept.
O C.
The maximum occurs at the function's y-intercept.
The minimum occurs at the function's y-intercept.
O D.
Answers
Answer:
B. The maximum occurs at the function's x-intercept.
Step-by-step explanation:
Given table:
\(\large\begin{array}{| c | c | c | c | c | c | c |}\cline{1-7} x & -5 & -4 & -3 & -2 & -1 & 0\\\cline{1-7} g(x) & -1 & 0 & -1 & -4 & -9 & -16\\\cline{1-7}\end{array}\)
From inspection of the table, we can see that:
\(g(-5) = -1\) and\(g(-3) = -1\)This indicates symmetry.
The line of symmetry is the mid-point between the two x-values.
Therefore, the line of symmetry is x = -4
The vertex (minima/maxima) is on the line of symmetry, therefore the vertex is at (-4, 0). As the function decreases as x → 0, the vertex is a maximum.
As the y-value of the vertex is 0, the maximum occurs at the function's x-intercept.
Answer:
B
Step-by-step explanation:
Finding the line of symmetry :
⇒ Two x-values have the same y-coordinate → (-5) and (-3)
⇒ This means the symmetry is exhibited and it lies between these 2 x-values
⇒ Line of symmetry : x = -4
=============================================================
Now, on plotting these points on a graph we see that this graph has a negative coefficient.
⇒ This means this graph will have a maximum point as the vertex
⇒ The vertex lies on the line of symmetry, hence the vertex (according to the graph and table) is (-4, 0)
Hence, we can say that the maximum occurs at the function's x-intercept.

Perimeter is 25 cm, find x 10 8.2 cm
Answers
2. Order the numbers from smallest to largest. *
Order the rational numbers listed below from smallest value to
largest value using the numbers 1, 2, 3, and 4.
Use the number 1 to represent the smallest value.
Use the number 4 to represent the largest value.
Order:
Rational
Number:
23
(0.7)
0.75
Your answer
Answers
Answer:
1. 0.7
2. 0.75
3. 23
Step-by-step explanation:
You didn't provide a fourth number.
HELP if a person runs 5 miles in 25 minute, how long will it take them to run 8 miles at the same rate?
Answers
Answer:1.6
Step-by-step explanation:
25/5=5
8/5=1.6
Answer:
40 MinutesStep-by-step explanation:
if 5miles = 25 minutes
then, 8 miles = X
hence X minutes
\(x = \frac{25minutes}{5miles} \times 8miles\)
X=40 minutesa student applies for ten different scholarships to various universities. seven of the scholarships pay for books. four scholarships include a meal ticket. two of the scholarships exclude meals and books. how many scholarships pay for both books and meals? use a venn diagram to illustrate and help solve this problem
Answers
The number of scholarships that pay for both books and meals is 1.
To solve this problem, we need to use the concept of set intersection. Let B be the set of scholarships that pay for books, and M be the set of scholarships that include a meal ticket. We want to find the number of scholarships that pay for both books and meals, which is the size of the set intersection B ∩ M.
From the problem statement, we know that:
|B| = 7 (seven scholarships pay for books)
|M| = 4 (four scholarships include a meal ticket)
We can use the inclusion-exclusion principle to find |B ∩ M|:
|B ∩ M| = |B| + |M| - |B U M|
We need to find the size of the union of the sets B and M, which includes all scholarships that pay for books, all scholarships that include a meal ticket, and possibly some scholarships that pay for both. From the problem statement, we know that there are two scholarships that exclude both meals and books, so we can subtract that from the union:
|B U M| = |B| + |M| - |B ∩ M| + 2
Substituting the known values, we get:
|B ∩ M| = |B| + |M| - |B U M| + 2
|B ∩ M| = 7 + 4 - (7 + 4 - |B ∩ M| + 2) + 2
|B ∩ M| = 1 + |B ∩ M|
Solving for |B ∩ M|, we get
|B ∩ M| = 1
Learn more about inclusion-exclusion principle here
brainly.com/question/27975057
#SPJ4
The given question is incomplete, the complete question is:
A student applies for ten different scholarships to various universities. seven of the scholarships pay for books. four scholarships include a meal ticket. two of the scholarships exclude meals and books. how many scholarships pay for both books and meals?
The joint probability density function of X and Y is given by f(x, y) = ce^(−x−2y) , 0 ≤ x < [infinity], 0 ≤ y < [infinity].
a. Find c.
b. Find P(X < 1, Y < 1).
c. Find P(X > Y ).
d. Find the distribution function of the random variable X − Y .
e. Are X and Y independent?
f. Compute the conditional density of X given that Y = y, where 0 ≤ y < [infinity].
Answers
a. the value of c is 2. b. the probability P(X < 1, Y < 1) is given by 1 - e^-1 - e^-2 + e^-3. c. P(X > Y ) is (-e^(-x-2y) + e^(-2y)y) + e^(-2y) - e^(-2y)y.
a. Finding the value of c:
To find the value of c, we need to integrate the joint probability density function (PDF) over the entire range of x and y and set it equal to 1, since the PDF must satisfy the normalization condition.
The joint PDF is given by f(x, y) = ce^(-x-2y)
∫∫f(x, y) dx dy = 1
∫∫ce^(-x-2y) dx dy = 1
Integrating with respect to x first:
∫[0,∞] ce^(-x-2y) dx = [-ce^(-x-2y)] [0,∞] = ce^(-2y)
Integrating the result with respect to y:
∫[0,∞] ce^(-2y) dy = [-1/2 * ce^(-2y)] [0,∞] = 1/2
Setting this equal to 1:
1/2 = 1/c
Solving for c:
c = 2
Therefore, the value of c is 2.
b. Calculating P(X < 1, Y < 1):
To find the probability P(X < 1, Y < 1), we need to integrate the joint PDF over the given region.
P(X < 1, Y < 1) = ∫[0,1] ∫[0,1] 2e^(-x-2y) dx dy
Integrating this expression, we get:
P(X < 1, Y < 1) = ∫[0,1] [-2e^(-x-2y)] [0,1] dy
= ∫[0,1] -2e^(-1-2y) + 2e^(-2y) dy
= [-e^(-1-2y) + e^(-2y)] [0,1]
= (-e^(-1-2) + e^(-2)) - (-e^(-1) + e^0)
= (-e^-3 + e^-2) - (-e^-1 + 1)
= 1 - e^-1 - e^-2 + e^-3
Therefore, the probability P(X < 1, Y < 1) is given by 1 - e^-1 - e^-2 + e^-3.
c. Finding P(X > Y):
To find the probability P(X > Y), we need to integrate the joint PDF over the region where X > Y.
P(X > Y) = ∫[0,∞] ∫[y,∞] 2e^(-x-2y) dx dy
Integrating this expression, we get:
P(X > Y) = ∫[0,∞] [-e^(-x-2y)] [y,∞] dy
= ∫[0,∞] -e^(-x-2y) + e^(-2y)y dy
= [-e^(-x-2y) + e^(-2y)y] [y,∞]
= (-e^(-x-2y) + e^(-2y)y) - (-e^(-2y) + e^(-2y)y)
= (-e^(-x-2y) + e^(-2y)y) + e^(-2y) - e^(-2y)y
Learn more about probability here
https://brainly.com/question/13604758
#SPJ11
Choose all the statements about the hexagon that are true.
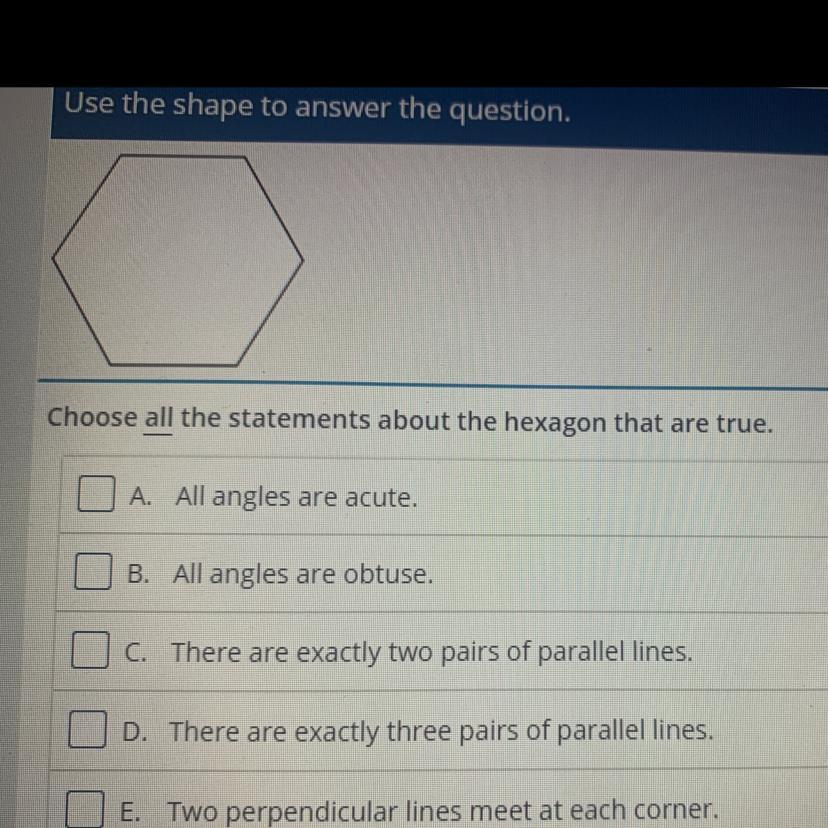
Answers
Answer:
B, D
Step-by-step explanation:
Sorry if I'm wrong. I dont know if E is right or not
Answer:
B, D
Step-by-step explanation
Select the correct answer.
Simplify the following polynomial expression.
3x(4x + 5) 4(-x - 3)(2x - 5)
20x² +59x - 15
O
O
1
20x² + 19x 60
4x² +59x + 60
-
4x2 + 19x + 15

Answers
Answer:
d. 4x² + 19x + 15.
Step-by-step explanation:
To simplify the given polynomial expression, we will apply the distributive property and combine like terms.
The expression is:
3x(4x + 5) - 4(-x - 3)(2x - 5)
Let's simplify each term step by step:
Expand the first term, 3x(4x + 5):
= 12x² + 15x
Expand the second term, -4(-x - 3)(2x - 5):
= -4(-x - 3)(2x) + (-4)(-x - 3)(-5)
= 8x² + 12x + 20x + 60
= 8x² + 32x + 60
Now, let's combine like terms:
12x² + 15x - 4x² - 32x - 60
Combining the x² terms and the x terms:
(12x² - 4x²) + (15x - 32x) - 60
= 8x² - 17x - 60
Therefore, the simplified form of the polynomial expression 3x(4x + 5) - 4(-x - 3)(2x - 5) is:
8x² - 17x - 60
Hence, the correct option is d. 4x² + 19x + 15.
Children should be encouraged to use the standard algorithms only, as these are widely used by adults.
TrueFalse
Answers
Solve 5h + 2(11 - h) = -5 (Find h. Explain each step please.)
Answers
Answer:
h = -9
Step-by-step explanation:
Distribute the 2 to the parentheses:
5h + 2(11 - h) = -5
5h + 22 - 2h = -5
Add like terms:
3h + 22 = -5
3h = -27
h = -9
Answer:
h = -4.5
Step-by-step explanation:
5h + 2(11-h) = -5
5h + 2(11-h)
+h +h
6h + 2 x 11 = -5
6h + 22 = -5
- 22 -22
6h = -27
/6 /6
h = -4.5
I hope this helps, I know the explanation is kinda confusing but I tried my best to explain :))
Aubree mowed 5 lawns in 4 hours. What was her rate of mowing in lawns per hour? Express your answer in simplest form.
Answers
Answer:
1.25 lawns/per hour
Step-by-step explanation:
Solve the system by graphing, then state the solution as an ordered pair
HELP ASAP!!!!!

Answers
Step-by-step explanation:
Simply graph the two equations....the intersection of the two graphs is the solution

a forest manager has pair of landsat satellite images for each of 1,250 plots of land. a proportion p of these plots were logged within the past ten years. each day she chooses a simple random sample of four plots, checks their image pairs, and categorizes them as logged or not by completing a spreadsheet like this:
Answers
A forest manager is using Landsat satellite images to determine whether 1,250 plots of land have been logged within the past ten years.
The proportion of logged plots is represented by 'p'.
The manager follows these steps daily:
1. Selects a simple random sample of four plots.
2. Examines the image pairs for each selected plot.
3. Categorizes the plots as logged or not logged.
4. Records the results in a spreadsheet.
The forest manager repeats this process daily to gather data on the proportion of logged plots (p) among the 1,250 plots of land.
For similar question on satellite.
https://brainly.com/question/30081351
#SPJ11
can anyone help me with this I tried to do it but i got to the wrong answer so i need help.

Answers
To use the quadratic formula, we need to identify the values of a, b, and c.
1. In this case, the equation is 4x² - 3x - 8 = 0, so a = 4, b = -3, and c = -8.
2. x = (-b ±√(b² - 4ac))/2a.
3. x = (3 ±√137)/8.
What is Quadratic Formula?The Quadratic Formula is a mathematical equation used to solve second-degree equations.
To use the quadratic formula, we need to identify the values of a, b, and c in the equation ax² + bx + c = 0.
In this case, the equation is
4x² - 3x - 8 = 0,
so a = 4, b = -3, and c = -8.
Once the values of a, b, and c are known, we can substitute them into the Quadratic Formula:
x = (-b ±√(b² - 4ac))/2a.
In this equation, a = 4, b = -3, and c = -8, so the equation becomes
x = (-(-3) ±√((-3)² - 4(4)(-8)))/2(4).
Simplifying, we get x = (3 ±√(9 + 128))/8.
Finally, solving for x yields x = (3 ±√137)/8.
Therefore, the solution to the equation is
x = (3 ±√137)/8.
For more questions related to equation
https://brainly.com/question/2228446
#SPJ1
Cindy can type 1080 words in 40 minutes, then how many words per minute can she type?
Answers
Answer:
27 words per minute
Step-by-step explanation:
1080/40= 27
Answer:
You can type 27 words/min
Step-by-step explanation
A box had 20 light bulbs, 5 of which are defective. A group of 8 bulbs is randomly selected.
a) what is the probability that none of the 8 bulbs are defective?
b) what is the probability that exactly one of the 8 is defective?
Answers
The probability that none of the 8 bulbs are defected is 0.12035, or approximately 12.04%. And the probability that exactly one of the 8 is defective will be 0.36256, or approximately 36.26%.
a) In the first case, we are required to calculate the probability that none of the 8 bulbs are defected. So, we need to obtain the probability of selecting 8 non-defected bulbs out of the 15 non-defected bulbs.
The probability of selecting one good bulb out of the 15 good bulbs is 3/4. Since we are selecting 8 bulbs without replacing it, the possibility of selecting 8 good bulbs out of the 15 good bulbs can be calculate here,
(15/20) x (14/19) x (13/18) x (12/17) x (11/16) x (10/15) x (9/14) x (8/13) = 0.12035
Hence , the probability that none of the 8 bulbs will be defective is calculated to be 0.12035, or approximately 12.04%.
b) Now to calculate the probability that exactly one of the 8 bulbs will be defected, there can be two possible cases which are needed to be considered. First case is selecting 1 defective bulb out of the 5 defective bulbs and 7 good bulbs out of the 15 good bulbs, and second, selecting 7 good bulbs out of the 15 good bulbs and 1 defective bulb out of the 5 defective bulbs.
The probability of selecting 1 defected bulb out of the 5 defected bulbs and 7 good bulbs out of the 15 good bulbs can be found by the calculation below :
(5/20) x (15/19) x (14/18) x (13/17) x (12/16) x (11/15) x (10/14) x (9/13) = 0.18128
The probability of selecting 7 working bulbs out of the 15 working bulbs and 1 defective bulb out of the 5 defective bulbs is the same as the probability of selecting 1 defected bulb out of the 5 defected bulbs and 7 good bulbs out of the 15 good bulbs, so the total probability of selecting exactly one defective bulb is calculated by the addition of the both probabilities
0.18128 + 0.18128 = 0.36256
Therefore, the probability of selecting exactly one of the 8 bulbs is defective is found to be 0.36256, or approximately 36.26%.
Learn more about probability :
https://brainly.com/question/11034287
#SPJ4
The graph of f(x)= x is translated 3 units down to form the graph of g(x). Which of the following is g(x)
Answers :
A: g(x)= -3x
B: g(x)= 3x
C: g(x)= x - 3
D: g(x)= x + 3

Answers
Answer:
I'll edit the answer and try to answer it, but where is the graph?
Answer:
C: g(x)= x- 3
Step-by-step explanation:
translated 3 units down means you go 3 down on the y-axis. Therefore it is g(x)= x-3
Nationwide, it is estimated that 40% of service stations have gas tanks that leak to some extent. A new program in California is designed to lessen the prevalence of these leaks. We want to assess the effectiveness of the program by seeing if the percentage of service stations whose tanks leak has decreased. To do this, we randomly sample 27 service stations in California and determine whether there is any evidence of leakage. In our sample, only 7 of the stations exhibit any leakage. Is there evidence that the new program is effective
Answers
Answer:
Since the calculated value of z= -1.496 does not fall in the critical region z < -1.645 we conclude that the new program is effective. We fail to reject the null hypothesis .
Step-by-step explanation:
The sample proportion is p2= 7/27= 0.259
and q2= 0.74
The sample size = n= 27
The population proportion = p1= 0.4
q1= 0.6
We formulate the null and alternate hypotheses that the new program is effective
H0: p2> p1 vs Ha: p2 ≤ p1
The test statistic is
z= p2- p1/√ p1q1/n
z= 0.259-0.4/ √0.4*0.6/27
z= -0.141/0.09428
z= -1.496
The significance level ∝ is 0.05
The critical region for one tailed test is z ≤ ± 1.645
Since the calculated value of z= -1.496 does not fall in the critical region z < -1.645 we conclude that the new program is effective. We fail to reject the null hypothesis .
Be sure to show your work and solve for f:
8=f−(13−2)
13-2=11
Answers
According to the given equation, the solution is f = 19
What is an equation?
An equation is a mathematical statement that shows that two expressions are equal. It consists of two sides separated by an equals sign (=).
We can start by simplifying the expression inside the parentheses:
f - (13 - 2) = f - 11
Then, we can rewrite the original equation using this simplified expression:
8 = f - 11
To solve for f, we want to isolate it on one side of the equation. We can do this by adding 11 to both sides:
8 + 11 = f - 11 + 11
19 = f
Therefore, the solution is:
f = 19
To know more about equations visit:
brainly.com/question/17499155
#SPJ1
Which of the following could be the interpretation of the distance vs time graph shown?
Which of these answers this Question, Is It 1, 2, or 3 that's in parentheses???
( 1.) A biker takes off on a course that begins with a small ramp. The biker bikes up a hill and across a flat portion of the course before heading down a steep descent.
( 2.) A driver leaver her house and slows down to make a stop at her neighbor's house. She then drives at a constant speed and stops at a house further down the street. After visiting with her neighbor, she quickly drives back home.
( 3.) A hiker begins hiking, but shortly after realized he left his water bottle in his car. He turns around to get his water bottle and then starts hiking again at a constant rate. The hiker stops for lunch at the furthest point of his hike and then hikes back at a quicker constant rate.

Answers
Answer:
3
Step-by-step explanation:
If you notice the y is the change in distance, so #3 has the best explanation.
Given the graph of f(x) above, find the value of integral(from 0 to 7) f(x)dx

Answers
The area under a curve between two points can be found out by doing the integral between the two points. In other words, the integral
\(\int ^7_0f(x)dx\text{ = Area betw}een\text{ x=1 and x=2 + Area betw}een\text{ x=2 and x=4 + Area betwe}en\text{ x=4 and x=5 - Area betw}een\text{ x=5 and x=7}\)Let's make a picture of the problem
Then, the integral will be equal to
\(\int ^7_0f(x)dx\text{ = Area black zone + Area red zone + Area gr}een\text{ zone - Area blue zone}\)The area of the black region is given by the area of the triangular part plus the rectangular part, that is
\(\begin{gathered} \text{ Area black zone = }\frac{1}{2}2\times1+2\times1 \\ \text{ Area black zone =}1+2 \\ \text{ Area black zone =}3 \end{gathered}\)The area of the red zone is the area of the rectangle
\(\begin{gathered} \text{ Area red zone = 2}\times2 \\ \text{ Area red zone =}4 \end{gathered}\)The green area is equal to the area of the green triangle,
\(\begin{gathered} \text{ Area gre}en\text{ zone=}\frac{1}{2}1\times2 \\ \text{ Area gre}en\text{ zone=}1 \end{gathered}\)and the blue area is the area of the blue triangle,
\(\begin{gathered} \text{ Area blue zone = }\frac{1}{2}2\times2 \\ \text{ Area blue zone = }2 \end{gathered}\)By substituting these values, the integral is given by
\(\int ^7_0f(x)dx\text{ = }3+4+1-2\)Therefore, the answer is:
\(\int ^7_0f(x)dx\text{ = }6\)
3.3615 rounded to the nearest tenth
Answers
The answer is 3.4
Because the 3 is in the tenths place. Since 6 is greater than 5 it gives 1 to the 3 which makes it a 4.
Sheri is making a large soccer ball for a stadium display. How many pentagons and hexagons does Sheri need altogether?
Clue 1: Sheri needs 3 pentagons for every 5 hexagons.
Clue 2: Sheri needs between 10 and 15 pentagons.
Clue 3: The number of hexagons is a multiple of 4.
Sheri needs __ pentagons and hexagons altogether.

Answers
The total amount of pentagons and hexagons that Shari does need altogether is given as follows:
32.
How to obtain the total amount?The total amount is obtained applying the proportions and ratios in the context of the problem.
Sheri needs 3 pentagons for every 5 hexagons, hence the equation is:
H = 5P/3.
Sheri needs between 10 and 15 pentagons, hence the possible amounts are given as follows:
10 pentagons: H = 5 x 10/3 = 16.67 hexagons.11 pentagons: H = 5 x 11/3 = 18.33 hexagons.12 pentagons: H = 5 x 12/3 = 20 hexagons -> multiple of 4.Hence the amount is of 12 pentagons and 20 hexagons, thus the amount is:
12 + 20 = 32 pentagons and hexagons altogether.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
Circle A has center of (6, 7), and a radius of 4 and circle B has a center of (2, 4), and a radius of 16. What steps will help show that circle A is similar to circle B? (6 points)
Group of answer choices
Translate circle A using the rule (x + 4, y + 3).
Rotate circle A 45° about the center.
Dilate circle A by a scale factor of 4.
Reflect circle A about the origin.
Answers
Answer is option-A and option-C
Translate and scale factor of Circle:
The translation rule can be expressed as ,
\((x,y) = > (x+a,y+b)\)
And the radius of dillated circle = scale factor * radius of original circle.
(Here),
First, Translate circle A using the rule (x + 4, y + 3)
i.e., to translate circle A we translate the Center of circle.
=> Center of Circle-A = (2 + 4 , 4 + 3)
=> Center of Circle-A = (6, 7)
scale factor = 4
Now, radius of dillate Circle-A i.e., the radius of circle-A is multiplied by 4.
i.e., radius of Circle A = 4 * 4 = 16.
Learn more about scale factor of circle here:
https://brainly.com/question/21481648?referrer=searchResults
#SPJ2
in a small fast food restaurant, on average, 10 customers come per hour. the restaurant can serve 12 customers per hour. on average, a customer spends 14 minutes in the restaurant. what is the average length of the line?
Answers
Therefore, the estimated average length of the line is 3 customers.
We can approach this problem by using the M/M/1 queueing model, which assumes a Poisson arrival process, an exponential service time distribution, and a single server.
In this case, the arrival rate (lambda) is 10 customers per hour, the service rate (mu) is 5 customers per hour (since the average servicem time is 14 minutes or 0.2333 hours), and there is one server.
The utilization factor (rho) is given by rho = lambda / mu = 10 / 5 = 2, which is greater than 1. This means that the system is not stable, and the queue will grow indefinitely.
To find the average length of the line, we can use Little's Law, which states that the long-term average number of customers in a stable system is equal to the long-term average arrival rate multiplied by the long-term average time spent in the system:
L = lambda * W
where L is the average number of customers in the system, lambda is the arrival rate, and W is the average time spent in the system.
In this case, since the system is not stable, we cannot use Little's Law directly. However, we can still estimate the average length of the line as follows:
Let's assume that the queue is at its steady-state when there are N customers in the system (i.e., being served plus waiting in the line). Then, the average length of the line (Lq) is:
Lq = N - 1
since one customer is being served and the remaining N-1 customers are waiting in the line.
The steady-state condition requires that the arrival rate equals the departure rate, which is the service rate in this case. Therefore, we can use the following formula to estimate N:
N = lambda / (mu - lambda)
Plugging in the values, we get:
N = 10 / (5 - 10) = -2
This negative value indicates that the system is not stable, and there are more customers arriving than the system can handle. However, we can still estimate the average length of the line as:
Lq = |N - 1| = |-2 - 1| = 3
To know more about average,
https://brainly.com/question/14896563
#SPJ11
Are the ratios 3:9 and 1:3 equivalent
Answers
Answer:
\(yes \\ 1 : 3 = 3 : 9\)
Step-by-step explanation:
yes.
\(1 : 3 = 3 : 9\)
Let see how is it possible,
\(3 \times 1 : 3 \times 3 = 3 :9 \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: 3 : 9 = 3 : 9\)
Also,
\(1 : 3= 3 \div 3 : 9 \div 3 \\ 1 : 3 = 1 : 3\)
hope this helps
brainliest appreciated
good luck! have a nice day!
what is the volume in cubic inches of a pyramid with a square base if the primeter of the base is 60 inches and the height is 20 inches
Answers
V = (1/3)(225)(20) = 1500 cubic inches. The volume of a pyramid with a square base can be calculated using the formula V = (1/3)Bh, where B is the area of the base and h is the height of the pyramid.
To find the area of the base, we need to first find the length of one side of the square base by dividing the perimeter (60 inches) by 4, which gives us 15 inches. Then, we can find the area of the base by squaring this length, which gives us 225 square inches. Plugging in the values of B = 225 and h = 20 into the formula, we get V = (1/3)(225)(20) = 1500 cubic inches.
we used the formula for the volume of a pyramid with a square base, which is V = (1/3)Bh. We then found the area of the base by finding the length of one side of the square base (perimeter divided by 4) and squaring it. Finally, we plugged in the values of the base area and height into the formula to get the volume in cubic inches.
To know more about perimeter refer to
https://brainly.com/question/30252651
#SPJ11
To make purple paint, we need to maintain a 3:2 ratio of red paint to blue paint. Red paint costs $20 a gallon and blue paint costs $25 a gallon. A coupon gives a 10% discount on red paint and a 20% on blue paint. If you have $500 for paint, what is the maximum amount of red blue paint you can buy to make purple paint?
Answers
Answer:
the most you can buy is 15 red paints and 10 blue. discounted the red paint is 18 and the blue is 20.
Step-by-step explanation:
18x15 is 270
20x10 is 200
so in total you would have spent 470
Write the equation of the trigonometric graph.
5
3
21
8
JVVV
-1
-2
-3
ch
즈
4
37
4

Answers
The trigonometric equation is:
y = 2*cos(2x) - 2
How to find the trigonometric equation?The general form of the equation is:
y = A*cos(k*x) + M
Where A is the amplitude, k is the angular frequency and M is the midline.
First, A is half of the difference between a maximum and a minimum, soi:
A = (0 - (-4))/2 = 2
M is the maximum minus the amplitude:
M = 0 - 2 = -2
So we have:
y = 2*cos(kx) - 2
And we can see that we have a maximum at 0 and the next one is at π/2.
So the value of K must be 2, because the number of maximums is doubled in that interval.
y = 2*cos(2x) - 2
Learn more about trigonometric equations at:
https://brainly.com/question/24349828
#SPJ1
There are 15 pieces of the same size candy in a bag. Four are banana flavored, three strawberry flavored, six cherry flavored, and two orange flavored. What would be the probability of picking a banana, cherry, or a strawberry flavored candy from the bag? Write your answer as a simplified fraction in a/b form.
Answers
Answer:
The answer is 7/15