Answers
Answer:
Both questions 5 and 7 are D
Step-by-step explanation:
Question 5:
Berry is 3. 17-3 = 14 this is the number of all of the other drinks.
14/17 = 0.82352941176 To turn into a percent, move the decimal two places to the right and then round to the nearest percent.
82% Letter D.
Question 7:
The graph is showing percents, so add heating and cooling together.
29 + 17 = 46 Letter D
Helping in the name of Jesus.
Related Questions
pls some help im so stuck im stuck as a cat in a tree dude plz help i
ill give u 100 pointes

Answers
Answer:
It's the positive i, no matter what i is equal to.
Sakura has a birdhouse with rectangular walls, a rectangular bottom, and a rectangular entry,like the one modeled below. She will paint the four outside walls but not the bottom or the roof of the birdhouse. What is the area that Sakura will paint? 140 in.2 300 in.2 160 in.2 320 in.2
Answers
Area of the birdhouse that Sakura will paint is 300 inches².
What is Area?Area of a two dimensional shape is the total region which is bounded by the object's shape.
Given that,
Sakura has a birdhouse with rectangular walls, a rectangular bottom, and a rectangular entry.
She will paint the four outside walls but not the bottom or the roof of the birdhouse.
We have to find the remaining area of the birdhouse without bottom and roof.
Area of the rectangular walls.
The two walls are of dimensions 10 inch × 6 inch and the other two are of the dimensions 10 inch × 10 inch.
One of the wall has a rectangular entry. so we have to subtract the area of the entry.
Total area = (10 × 6) + (10 × 6) + (10 × 10) + [(10 × 10) - (4 × 5)]
= 60 + 60 + 100 + [100 - 20]
= 300 inches²
Hence the total area needed to paint is 300 inches².
Learn more about Area here :
https://brainly.com/question/20693059
#SPJ2

Consider the system of equations
below. What is the solution of the
system?
y=4x-8
4x + 2y = 20
Answers
Answer:
x = 3, y = 4
Step-by-step explanation:
Substitute 4x - 8 in for y and then solve for x:
4x + 2(4x - 8) = 20
Then, 4x + 8x - 16 = 20 --> 12x = 36 --> x = 3.
Once you have x, you can solve for y.
y = 4x - 8 = 4(3) - 8 = 12 - 8 = 4
So, x = 3, y = 4
......//...//../././//..//.././.?
Answers
Answer:.//./././/..
Step-by-step explanation:.././././..././..././//...../
4 5/7 + 3 3/4 = ??
Simplify ur answer
Show ur work
Answers
Answer:
237/28
Step-by-step explanation:
4 5/7=33/7
3 3/4=15/4
----------------
33/7+15/4=132/28+105/28=237/28
Answer:
8 13/28 or as a decimal: 8.46
Step-by-step explanation:
Rewrite the sum:
(4+3)+(5/7+3/4)
Add the numbers 4+3:
7+(5/7+3/4)
Add the fractions:
7+41/28
Convert the improper fraction into a mixed number:
7 + 1 13/28
Write the mixed number as a sum of the whole number and the fractional part:
7+1+13/28
Add the numbers 7+1 and then there is your answer!
8 13/28
If your paper, quiz, homework, etc says decimal form or alternative form then the decimal form is 8.46 and the alternate form is 237/26. But 8 13/28 cannot be reduced any lower.
Tell whether the ordered pair (4, -2) is a solution to
2x - y > -5
y <-3x - 3
Answers
b. if a is a 35 matrix and t is a transformation defined by t(x)ax, then the domain of t is .
Answers
For the matrix the true statement is given by option d. Both A and B are false.
Let's analyze each statement of the matrix as follow,
A) If A is a 3 times 5 matrix and T is a transformation defined by T(x) = Ax, then the domain of T is R⁵.
This statement is false.
The domain of the transformation T is not R⁵.
The domain of T is determined by the dimensionality of the vectors x that can be input into the transformation.
Here, the matrix A is a 3 times 5 matrix, which means the transformation T(x) = Ax can only accept vectors x that have 5 elements.
Therefore, the domain of T is R⁵, but rather a subspace of R⁵.
B) If A is a 3 times 2 matrix, then the transformation x right arrow Ax cannot be onto.
This statement is also false.
The transformation x → Ax can still be onto (surjective) even if A is a 3 times 2 matrix.
The surjectivity of a transformation depends on the rank of the matrix A and the dimensionality of the vector space it maps to.
It is possible for a 3 times 2 matrix to have a rank of 2,
and if the codomain is a vector space of dimension 3 or higher, then the transformation can be onto.
Therefore, as per the matrix both statements are false, the correct answer is d. Both A and B are false.
Learn more about matrix here
brainly.com/question/29132693
#SPJ4
The above question is incomplete, the complete question is:
Which of the following best characterizes the following statements:
A) If A is a 3 times 5 matrix and T is a transformation defined by T(x) = Ax, then the domain of T is R^5
B) If A is a 3 times 2 matrix, then the transformation x right arrow Ax cannot be onto
a. Only A is true
b. Only B is true
c. Both A and B are true
d. Both A and B are false
according to a recent student poll, \frac{5}{7} of the 21 members of the finance club are interested in a career in investment banking. if two students are chosen at random, what is the probability that at least one of them is interested in investment banking?
Answers
The probability that at least one of them is not interested in investment banking is 13/14.
What is a probability?It is a branch of mathematics. The possibility of the outcome of any random event is termed as probability. The range of the probability must be between o to 1. Here o indicates impossibility of an event and 1 indicates certainty. Probability can be expressed in proportions. Probability deals in finding the occurrence of an event.
Probability of the first person who is not interested in investment banking is 6/21
Probability of the second person who is not interested in investment banking and also first person was not interested then it is taken as 5/20.
probability that at least one is not interested in investment banking
=1- The probability that neither one of them is not interested in investment banking
=1-((6/21)×(5/20)
=13/14
Therefore, the probability that at least one of them is not interested in investment banking is 13/14.
To know more about probability, visit:
https://brainly.com/question/11234923
#SPJ4
Math help please show work

Answers
Answer:
7 in
Step-by-step explanation:

Answer:
a = 7 in
Step-by-step explanation:
\(Area = \frac{a+b}{2} \times h\\\\26.25 = \frac{a + 10.5}{2} \times 3\\\\26.25 \times 2 = (a+ 10.5) \times 3\\\\52.5 = (A + 10.5) \times 3\\\\\frac{52.5}{3} = a + 10.5\\\\17.5 = a + 10.5\\\\a = 17.5 - 10.5 = 7\)
a real number $a$ is chosen randomly and uniformly from the interval $[-20, 18]$. the probability that the roots of the polynomial $x^4 2ax^3 (2a - 2)x^2 (-4a 3)x - 2$ are all real can be written in the form $\dfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. find $m n$.
Answers
Since, m and n are prime positive number. Therefore,
m + n = 18 + 19 =037
The polynomial we are given is rather complicated, so we could use Rational Root Theorem to turn the given polynomial into a degree-2 polynomial. With Rational Root Theorem, x = 1, -1, 2, -2 are all possible rational roots. Upon plugging these roots into the polynomial, x = -2 and x = 1 make the polynomial equal 0 and thus, they are roots that we can factor out.
The polynomial becomes:
(x - 1)(x + 2)(x^2 + (2a - 1)x + 1)
Since we know 1 and -2 are real numbers, we only need to focus on the quadratic.
We should set the discriminant of the quadratic greater than or equal to 0.
(2a - 1)^2 - 4 ≥ 0.
This simplifies to:
a ≥ 3/2
or,
a ≤ - 1/2
This means that the interval (- 1/2 ,3/2) is the "bad" interval. The length of the interval where a can be chosen from is 38 units long, while the bad interval is 2 units long. Therefore, the "good" interval is 36 units long.
36/38 = 18/19
18+ 19 = 037
Learn more about Prime Positive Number :
https://brainly.com/question/24635729
#SPJ4
15. What is the length of the diagonal for the given rectangular prism to the nearest whole unit?
0 10 cm
011 cm
06 cm
O13 cm
Length = 8 cm
Width =3 cm
Height = 7 cm
Answers
c = 11.05 ≈ 11 cm. When the diagonal length for the rectangular prism is given is to the nearest whole unit, the correct answer is B.
what is length ?A quantity known as length has the ability to calculate approximate distance between two areas. In addition to height the breadth, it creates an object's length. Children will learn about length in math lessons to help them solve practical challenges both inside and outside of the classroom. the length or width that is possible to measured; a thing's greatest or longest dimension. 10 feet in length. Table of Metric units, Metric System Table: The length characteristic. The quantity or measurement between two points is the definition of length. In other words, a geometric arrangement or object's largest two or highest three dimensions.
given
Start by calculating the length of the base's diagonal using the Pythagorean theorem:
a² + b² = c²
Fill in the equation with the length and width:
8² + 3² = c²
64 + 9 = c²
73 = c²
c ≈ 8.54 cm
Using our estimated diagonals for the base and the height, we can now determine the prism's diagonal's length. Apply the same formula:
(8.54)² + 7² = c²
73 + 49 = c²
122 = c²
√122 = c
c = 11.05 ≈ 11 cm. When the diagonal length for the rectangular prism is given is to the nearest whole unit, the correct answer is B.
To know more about length visit :-
https://brainly.com/question/30100801
#SPJ1
Evaluate the given integral. (Hint: Exploit the fact that D is symmetric with respect to both axes.) //g(x2 tan (z) + ã¡ + 3)dA, where D = {(x, y)|x2 + y2 4) Gn
Answers
To evaluate the given integral, we can use the fact that D is symmetric with respect to both axes. This means that we can rewrite the integral as:
∫∫D g(x^2 tan(z) + ã¡ + 3) dA
= 4 ∫∫D g(x^2 tan(z) + ã¡ + 3) dxdy where we have used the symmetry of D to change the limits of integration.
Next, we can convert to polar coordinates, which is particularly convenient since D is defined in terms of x and y in terms of their distance from the origin. Specifically, we can substitute x = r cos(θ) and y = r sin(θ), and also use the identity tan(z) = sin(z) / cos(z) = y/x:
∫∫D g(x^2 tan(z) + ã¡ + 3) dxdy
= 4 ∫θ=0^2π ∫r=2^√(9 - r^2 cos^2(θ)) 0 g(r^2 sin(θ) cos(θ) + ã¡ + 3) rdrdθ where we have used the equation of the circle r^2 = x^2 + y^2 = 4 to set the limits of integration for r.
Now we can simplify the integrand by noting that r^2 sin(θ) cos(θ) = (r^2/2) sin(2θ). We also have the constant term ã¡ + 3, which does not depend on r or θ. Thus, we can pull it out of the integral:
4 ∫θ=0^2π ∫r=2^√(9 - r^2 cos^2(θ)) 0 g((r^2/2) sin(2θ) + ã¡ + 3) rdrdθ
= (ã¡ + 3) 4 ∫θ=0^2π sin(2θ) dθ ∫r=2^√(9 - r^2 cos^2(θ)) 0 g(r^2/2) rdr
The inner integral can be evaluated using the substitution u = r^2/2, so that rdr = du/sqrt(2), and the limits of integration become u = 0 to u = 9/2 cos^2(θ). We can then use the fact that g is an arbitrary function, so we can write:
∫r=2^√(9 - r^2 cos^2(θ)) 0 g(r^2/2) rdr
= ∫u=0^9/2cos^2(θ) g(u) du/sqrt(2)
Finally, we can substitute back into the original expression:
4 ∫θ=0^2π sin(2θ) dθ ∫r=2^√(9 - r^2 cos^2(θ)) 0 g(r^2/2) rdr
= (ã¡ + 3) 4 ∫θ=0^2π sin(2θ) dθ ∫u=0^9/2cos^2(θ) g(u) du/sqrt(2)
= 2π (ã¡ + 3) ∫u=0^9/2 g(u) du
Learn more about arbitrary function here:
https://brainly.com/question/15688392
#SPJ11
A clinical laboratory scientist performs 30 replicate hemoglobin determinations on a single blood sample. When statistics are used to determine the precision of the method, the mean is 13.8 g/dL and 1 SD is 0.1 g/dL. This means that 95.5% of the results on this specimen lie: 9).
A) between 13.6 and 14.0 g/dL.
B) between 13.4 and 14.2 g/dL.
C) between 13.7 and 13.9 g/dL.
D) between 13.5 and 14.1 g/dL.
Answers
The correct option is (A) between 13.6 and 14.0 g/dL.
A clinical laboratory scientist performs 30 replicate hemoglobin determinations on a single blood sample. When statistics are used to determine the precision of the method, the mean is 13.8 g/dL and 1 SD is 0.1 g/dL. This means that 95.5% of the results on this specimen lie between 13.6 and 14.0 g/dL.What is Standard deviation?Standard deviation measures the spread of a dataset. In the context of science experiments, it's a way of measuring how much the individual results of an experiment deviate from the average value.
The standard deviation (SD) is the most commonly used measure of the spread of a dataset. It measures the degree of variability in a set of measurements, in this case, hemoglobin levels. The mean, also known as the average, of these hemoglobin measurements is 13.8 g/dL.Therefore, the 95.5 percent of the results of this specimen lie between 13.6 and 14.0 g/dL. So, the correct option is (A) between 13.6 and 14.0 g/dL.
Learn more about the word hemoglobin here,
https://brainly.com/question/5385828
#SPJ11
A bag of sweets contains 11 red sweets and 7 green sweets . Alice chooses a swee from the bag at random , eats it , then chooses a second sweet at random .
What fractions should go in the boxes marked A,B,C below? Give your answers in their simplest form
Answers
The probability of one red sweet and one green sweet is 1/77
How to determine the probability of one red sweet and green sweetFrom the question, we have the following parameters that can be used in our computation:
Red sweet = 11
Green sweet = 7
This means that
P(Red) = 1/11
P(Green) = 1/7
So, the required probability is
P = 1/11 * 1/7
Evaluate
P = 1/77
Hence, the probability is 1/77
Read more about probability at
https://brainly.com/question/251701
#SPJ1
factorize = n!+(n-1)!
Answers
Answer:
Hello,
Step-by-step explanation:
n! + (n-1)!
=(n-1)! * n+ (n-1)!
=(n-1)! * (n+1)
Calculate the angular velocity of the earth about its axis.
Answers
By dividing the angle of rotation by the duration of one rotation, the angular velocity of the Earth around its axis can be determined. The time it takes the Earth to complete one full rotation, which is equivalent to 360 degrees or 2 radians, is roughly 24 hours.
Angle change divided by time change equals angular velocity (v), as follows:
ω = θ / t
We can substitute the following values into the equation since the Earth completes one rotation every 24 hours:2 radians each day equals.
By multiplying by 3600 (the amount of seconds in an hour), we may convert the time from hours to seconds:
2 radians are equal to (24 hours * 3600 seconds/hour)
Condensing the equation:
learn more about angular here :
https://brainly.com/question/15487308
#SPJ11
2/3 + 2/7 HELP ASAP PLEASE
Answers
Answer:
step by step explanation is given above .

please, help me out !!

Answers
Answer:
Correct Statements:
1. The graph of A(t) decreases exponentially
4. The graph of A(t) has a y-intercept at (0,1200)
5. Every year, the cell phone loses 8% of its value.
Step-by-step explanation:
Exponential functions are in the form \(y=a(b)^x\), meaning this is a exponential function, so it cannot be linear
a on the exponential function form represents the initial value, otherwise known as the y-intercept, and 1200 is a for the given equation
To find the multiplier, you do 1 -r, and since its 0.92, we do 1-0.92 = 0.08 value per year.
can someone pls help

Answers
The required area of the parallelogram and pentagon is 91 unit² and 75 unit².
What is surface area?The surface area of any shape is the area of the shape that is faced or the Surface area is the amount of area covering the exterior of a 3D shape.
A parallelogram in is shown in figure 1 with the dimensions height = 7 and base = 13,
Area of the parallelogram = 13 × 7 = 91 unit²
Now,
A pentagon is shown in figure 2,
Area of the pentagon = 5 [1/2 × height × side]
= 5 [1/2 × 5 × 6]
= 75 suqare units.
Thus, the required area of the parallelogram and pentagon is 91 unit² and 75 unit².
Learn more about the surface area here: https://brainly.com/question/2835293
#SPJ1
The polygons are similar. Find the value of x.

Answers
Answer:
x= 28
Explanation:
. (a) In the following model for the growth of rabbits, foxes, and hu- mans, R' = R + .3R - 17 - 2H F = F + 4R ..2F .3H H' = H + .IR + 1F + 1H determine the sum and max norms of the coefficient matrix A. (b) If the current vector of population sizes is p = [10, 10, 10], de- termine bounds (in sum and max norms) for the size of p' Ap. Compute p' and see how close it is to the norm bounds. (c) Give a sum norm bound on the size of population vector after four periods, p(4).
Answers
In a population growth model for rabbits, foxes, and humans, the sum norm of the coefficient matrix is 4.5 and the max norm is 4.4. Using these norms, we can bound the size of the population vector after one period.
(a) To find the coefficient matrix A, we identify the coefficients of the variables R, F, and H in the given model equations. Once we have A, we can calculate its sum norm by adding up the absolute values of its elements and its max norm by taking the maximum absolute value among its elements. (b) Given the population vector p = [10, 10, 10], we can calculate p'Ap by multiplying p' (transpose of p) with A and then with p. The resulting value will provide the bounds for the size of p'Ap in both sum and max norms. Comparing this value with the norm bounds will indicate how close they are. (c) To determine the sum norm bound for the population vector after four periods, p(4), we need to multiply A by itself four times and calculate the sum of the absolute values of its elements. This sum will give us the desired sum norm bound.
To know more about population growth here: brainly.com/question/18415071
#SPJ11
Based on the information given, compute yearly total dividends as well as dividends per share paid to common and preferred stockholders. There are 5,000 shares of $50 par value preferred stock outstanding, and 25,000 shares of common stock outstanding. Preferred stock has an 8 percent guaranteed rate of return. Dividends are declared of $1. 25 per share of common stock, together with the guaranteed rate for preferred stock. Common Stock: $
Preferred Stock: $
Answers
1. Yearly total dividends paid are $151,250.
2. The dividends per share are $1.25 for common stockholders
3. The dividends per share are $4 for preferred stockholders.
What are yearly total dividends and dividends per share?We must calculate amount of dividends paid to the preferred stockholders in order to get dividends per share for common and preferred stockholders.
The per dividends paid to the preferred stockholders is:
= $50 par value x 8% guaranteed rate of return
= $4 per share
The total dividends paid to preferred stockholders:
= $4 per share x 5,000 shares
= $20,000
The per dividends paid to those stockholder is calculated as:
= Common stock + Preferred stock
= $1.25 per share + $4 per share
= $5.25 per share
The total dividends paid to common stockholders:
= $5.25 per share x 25,000 shares
= $131,250.
Read more about dividends
brainly.com/question/2960815
#SPJ4
In the image, point A marks the center of the circle. Which two lengths must form a ratio of 1:2?
a. HI:EF
b. EF:AD
c. AD:AH
d. AH:HI
e. BC:HI
Answers
From the given circle image, we can say that the two lengths that must form the ratio of 1:2 is; d. AH:HI
How to find the ratio lengths?From the image attached, we are given that Point A is the center of the circle.
Let us access each of the options to find out which one of the two lengths must form a ratio of 1:2;
Option a. HI:EF
We see that both HI and EF are diameters of the circle. Thus, their ratio cannot be equal to 1:2.
Option b. EF:AD
We see that EF is the diameter while s the radius, we can say that;
Diameter = 2 × Radius
Thus;
EF : AD = 2:1
Option c: AD : AH
We see that both D and AH are radius and as such their ratio can never be 1:2.
Option d : AH:HI
We see that AH is the radius while HI is the diameter. Thus, their ratio will be; AH:HI = 1:2
Option e; BC:HI
We see that BC is a chord and we are not given its' length and so we can't ascertain if it forms a ratio of 1:2 with HI
Read more about ratio length at; https://brainly.com/question/11983035
#SPJ1

Help plz I will give brainliest if it's right
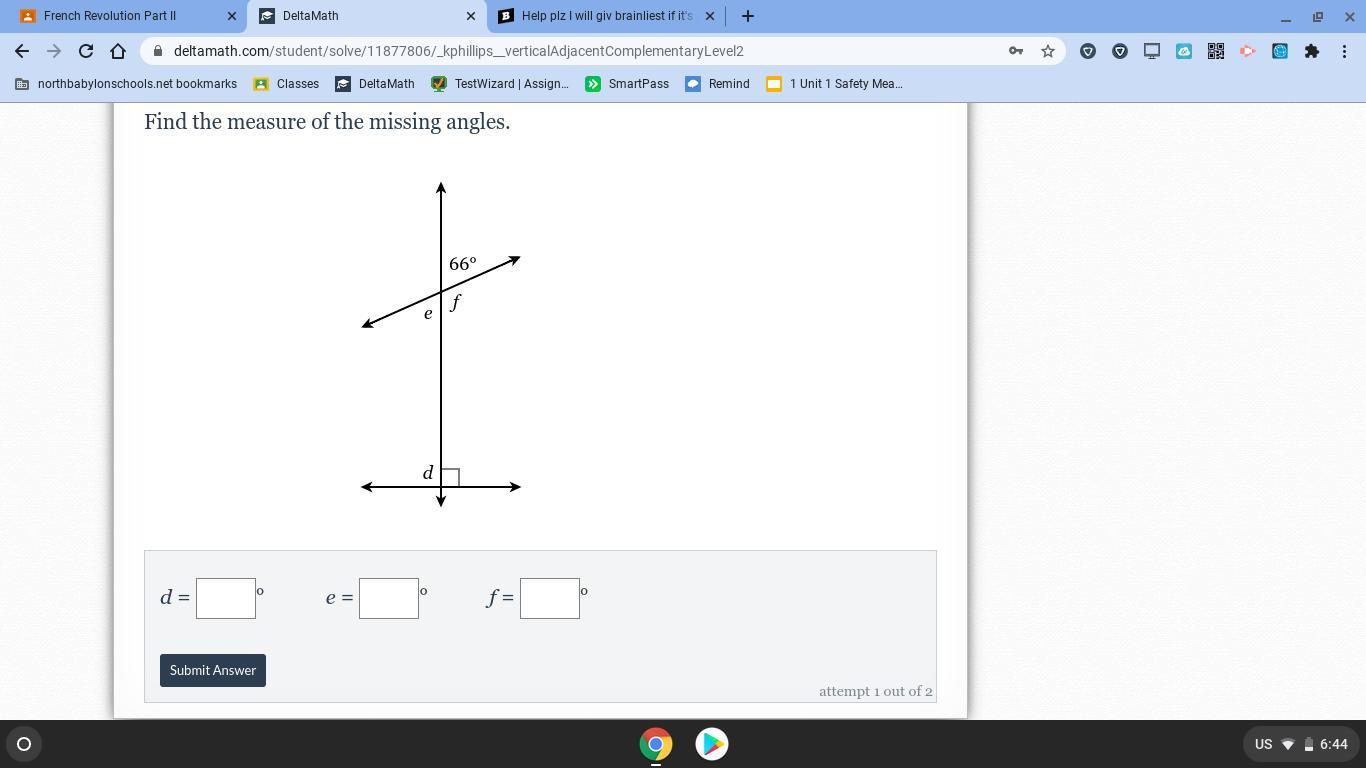
Answers
Answer:
66
Step-by-step explanation:
let, the missing angle be x.
x= 66°{being the corresponding angle}
: the value of missing angle is 66°
Pam has 228 ounces of lemonade. she pours the lemonade into
8-ounce cups, filling as many as she can until all the lemonade is
gone. the last cup is not completely full. how much lemonade is
in the last cup?
a: 4ounces
b: 8 ounces
c: 12 ounces
d: 3 ounces
Answers
The last cup contains 4 ounces of lemonade. Option (a) is correct.
Pam has 228 ounces of lemonade and she pours it into 8-ounce cups. To determine the amount of lemonade in the last cup, we divide the total amount of lemonade by the size of each cup.
228 ounces ÷ 8 ounces = 28 cups with a remainder of 4 ounces.
Since the last cup is not completely full, the remaining 4 ounces of lemonade are in the last cup. This means option (a), which states that there are 4 ounces in the last cup, is the correct answer.
By dividing the total amount of lemonade by the cup size and considering the remainder, we can determine the quantity of lemonade in the last cup, which in this case is 4 ounces.
To know more about ounces,
https://brainly.com/question/29374025#
#SPJ11
A small business assumes that the demand function for one ofits new products can be modeled by p=Cekx. When p=$45, x= 1000 units and when p=$40, x = 1200 units.
a) solve for C and k.
b) Find the values of x and p that will maximize the revenuefor this product
Answers
a) As per the demand function, the solution for C is $160, and k is 0.0006
b) The optimal price and quantity that will maximize the revenue for the small business's new product are approximately $48.56 and 414 units, respectively.
To solve for C and k, we need to eliminate one of the variables, either C or k. We can achieve this by taking the ratio of the two equations, which yields:
\($45/40 = (Cek(1000))/(Cek(1200))$\)
Simplifying the equation, we get:
\($1.125 = e^{200k}$\)
Taking the natural logarithm of both sides, we get:
ln(1.125) = 200k
Therefore, k=ln(1.125)/200 = 0.0006
Substituting this value of k in one of the equations, we can solve for C. We can use the first equation:
\($45=Ce^{ln(1.125)*1000/200}$\)
Simplifying, we get:
C=180/1.125 ≈ $160
To find the quantity that maximizes revenue, we need to take the derivative of the revenue function with respect to x and set it equal to zero, and then solve for x.
Taking the derivative of R(x), we get:
\(R'(x) = 160e^{(ln(1.125)x/200)} + 160x\times(ln(1.125)/200)\times e^{(ln(1.125)x/200)}\)
Setting R'(x) = 0, we get:
\(160e^{(ln(1.125)x/200)} + 160x\times(ln(1.125)/200)\times e^{(ln(1.125)x/200)}=0\)
Simplifying the equation, we get:
\(e^{(ln(1.125)x/200)} = -x\times(ln(1.125)/200)\)
Taking the natural logarithm of both sides, we get:
\(ln(e^{(ln(1.125)x/200)}) = ln(-x\times(ln(1.125)/200))\)
x = -200/ln(1.125) ≈ -414.72
The negative value of x is not meaningful in this context, so we can ignore it. Therefore, the quantity that maximizes revenue is approximately 414 units.
To find the corresponding price that yields the maximum revenue, we can substitute x = 414 in the demand function:
p = \(160e^{(ln(1.125)*414/200)}\)≈ $48.56
To know more about demand function here
https://brainly.com/question/28198225
#SPJ4
Find the perimeter. Simplify your answer.
6a-5
a+1
a+1
6a-5

Answers
2(6a - 5) + 2(a + 1) =
= 12a - 10 + 2a + 2 =
= 12a + 2a - 10 + 2 = 14a - 8
Answer:
14a-8
Step-by-step explanation:
A perimeter is the sum of the length of each side. So we can find the perimeter by adding: (a+1)+(a+1)+(6a-5)+(6a-5).
Combine like terms to get: 14a+2-10 = 14a-8.
Without knowing what a is, the perimeter is 14a-8.
Part 2: Parallel Lines and Transversals
6.) Name the relationship between <4 and <6: __________
7.) Name the relationship between <4 and <2: __________
8.) Name the relationship between <2 and <3: __________
9.) Name the relationship between <2 and <8: __________
10.) Name the relationship between <3 and <7: __________
11.) Name the relationship between <2 and <5: __________
12.) Name the relationship between <5 and <1: __________
~Word Bank
*Corresponding Angles
*Alternate Exterior Angles
*Supplementary
*Parallel
*Transversal
*Alternate Interior Angles
*Consecutive Interior Angles
*Vertical Angles

Answers
6) alternate exterior angles
7) vertical angles
8) supplementary
9) alternate interior angles
10) corresponding angles
11) consecutive interior angles
12) corresponding angles
1. What value of x makes a true equivalent fraction statement.
8/40=x/30
Answers
Hey there!
=> 8/40 = x/30
=> (40)(x) = (8)(30)
=> 40x = 240
Divide both sides by 40
=> 40x/40 = 240/40
=> x = 240/40
=> x = 6
Therefore, the value of x makes a true equivalent fraction statement is 6
Value of x is:
x = 6Step-by-step explanation:
Given Fraction,
\( \dfrac{8}{40} = \dfrac{x}{30} \)
Further we can solve by cross multiplication,
\( \sf 40 \times x = 8 \times 30 \)
\( \sf 40x = 240 \)
Divide both sides by 40,
\( \sf \dfrac{40x}{40} = \dfrac {240}{40} \)
\( \sf x = 6 \)
Verifying our answer.
Simply put the value of x in the given fraction ,
\( \dfrac{8}{40} = \dfrac{6}{30} \)
We know that,
8 × 5 = 406 × 5 = 30\( \sf \dfrac{1}{5}= \dfrac{1}{5}\)
Hence, x = 6 makes a true equivalent fraction statement.
A customer paid for different items at a farmer's
market. Find the cost for 1 pound for the
following item
$5 for 4 pounds of apples
Answers
You simply do $5/4 and get 1.25
