Student scores on Professor Combs' Stats final exam are normally distributed with a mean of 76 and a standard deviation of 7.2Find the probability of the following:**(use 4 decimal places)**a.) The probability that one student chosen at random scores above an 81. b.) The probability that 20 students chosen at random have a mean score above an 81. c.) The probability that one student chosen at random scores between a 71 and an 81. d.) The probability that 20 students chosen at random have a mean score between a 71 and an 81.
Answers
a) \(IP=0.2437.\)
b) \(IP=0.0009.\)
c) \(IP= 0.5126.\)
d) \(IP=0.9982.\)
Step-by-step explanation:a.) The probability that one student chosen at random scores above an 81.x= 81
u= 76
s= 7.2
\(Z=\frac{(81)-(76)}{7.2}=0.6944\)
(Check the attached images) Using the function "NORM.S.DIST" on Microsoft Excel we get:
IP(S>81)= 0.2437.
b.) The probability that 20 students chosen at random have a mean score above an 81.Now, we need to calculate the Z value with the following formula, because we are nor working with a sample (the 20 students):
\(Z=\frac{x-u}{(\frac{s}{\sqrt{n} } )}\)
"n" is the sample size, and it equals 20 for this case.
\(Z=\frac{81-76}{(\frac{7.2}{\sqrt{20} } )}=3.1056\)
\(IP(x > 81,n=20)=0.0009\)
c.) The probability that one student chosen at random scores between a 71 and an 81.The answer to this problem is given by:
IP= (Probability of a student scoring 81 or less)-(Probability of a student scoring 71 or less)
1. For the probability of a student scoring 81 or less:
\(Z=\frac{81-76}{7.2} =0.6944\)
\(IP(Z < 0.6944)=0.7563\)
2. For the probability of a student scoring 81 or less:
\(Z=\frac{71-76}{7.2} =-0.6944\)
\(IP(Z < -0.6944)=0.2437\)
IP=0.7563-0.2437= 0.5126.
d.) The probability that 20 students chosen at random have a mean score between a 71 and an 81.\(Z_{1} (x < 71,n=20)=-3.1056\\ \\Z_{2} (x < 81,n=20)=3.1056\\ \\IP(Z < 3.1056)=0.9991\\ \\IP(Z < -3.1056)=0.0009\\ \\IP(Z_{1} < Z < Z_{2} )=0.9991-0.0009=0.9982\)
Please check the attached document to better understand the process for calculating all the answers.-------------------------------------------------------------------------------------------------------
Learn more about probabilities from the normal distribution here:https://brainly.com/question/30016719
https://brainly.com/question/28227075
https://brainly.com/question/28227076
Related Questions
Which function includes the pony (0, 9) on its graph?
Answer choices:
A: x=9
B: y=9x^2
C: y= √x + 3
D: y= -1/3x + 9
Answers
Answer:
D is d because when You have to do they graph You have multiplicar
1) 2 + 24 + 40 + 39- (33 - 30)
=
Answers
Answer:
102
Step-by-step explanation:
hope this helps
Answer:
2+24+40+39-(33-30)
105-33+30
135-33
132
Is d = 6 a solution to the inequality below?
13 < d + 3
Answers
Answer:
Step-by-step explanation:
d = 6 would not be a solution to the inequality below because it would make the inequality untrue! Plugging in, we get:
13 < d + 3
13 < 6 + 3
13 < 9
We know that 9 is not a solution to the inequality!
To solve, we isolate the d, and from there we can find all values that are a solution to the inequality to the solution!
\(13 < d + 3\\\\13 - 3 < d\\\\10 < d\)
Thus, one can say that the solutions to the inequality are: [R, d > 10]!
PLS HELP :( i’ve been trying to understand this but i cant. please explain this if you know how to do it pleaseee

Answers
Answer:
\(\huge\boxed{\sf x = 17}\)
Step-by-step explanation:
Since m is a straight line, its measure is 180 degrees.
So,
2x + 5 + 8x + 5 = 180
2x + 8x + 5 + 5 = 180
10x + 10 = 180
10x = 180 - 10
10x = 170
Divide both sides by 10
x = 17
\(\rule[225]{225}{2}\)
Hope this helped!
~AH1807Peace!please answer with explanation

Answers
Answer: 624
Step-by-step explanation:
The area of a rhombus is the product of the diagonals divided by 2 so the area of the rhombus in this case is 12 * 16 / 2 or 96 multiply with 6.5 we get 624 so that's the answer
0.834
0.861
0.927
0.877
0.831
0.925
0.912
0.83
0.849
0.933
0.884
find mean, median, maximum, minimum, and mode
Answers
Mean ≈ 0.874
Median ≈ 0.877
Maximum = 0.933
Minimum = 0.83
Mode = None
To find the mean, median, maximum, minimum, and mode of the given numbers:
Mean: The mean is the average of a set of numbers.
To calculate the mean, add up all the numbers and divide the sum by the total count.
Mean = (0.834 + 0.861 + 0.927 + 0.877 + 0.831 + 0.925 + 0.912 + 0.83 + 0.849 + 0.933 + 0.884) / 11
Mean ≈ 0.874
Median: The median is the middle value when the numbers are arranged in ascending or descending order.
Since there are 11 numbers, the median would be the 6th number when arranged in order.
Arranging the numbers in ascending order:
0.83, 0.831, 0.834, 0.849, 0.861, 0.877, 0.884, 0.912, 0.925, 0.927, 0.933
Median ≈ 0.877
Maximum: The maximum is the largest value among the given numbers.
Maximum = 0.933
Minimum: The minimum is the smallest value among the given numbers.
Minimum = 0.83
Mode: The mode is the value(s) that appear most frequently in the given numbers.
If there is no value that appears more than once, there is no mode.
For such more questions on Mean
https://brainly.com/question/21133077
#SPJ8
In art class students are mixing blue and red paint to make purple paint. Isaiah mixes 3 cups of blue paint and 7 cups of red paint. Casho mixes 4 cups of blue paint and 13 cups of red paint. Use Isaiah and Casho's percent of red paint to determine whose purple paint will be redder.
Answers
Based on the percent of red paint, Casho's purple paint will be redder than Isaiah's.
To determine whose purple paint will be redder based on the percent of red paint, we need to compare the ratios of red paint to the total paint used by Isaiah and Casho.
Isaiah's Ratio:
Isaiah mixes 3 cups of blue paint and 7 cups of red paint, making a total of 3 + 7 = 10 cups of paint.
To calculate the percent of red paint, we divide the amount of red paint (7 cups) by the total amount of paint (10 cups) and multiply by 100 to get the percentage:
Red paint percentage for Isaiah = (7 cups / 10 cups) * 100 = 70%
Casho's Ratio:
Casho mixes 4 cups of blue paint and 13 cups of red paint, making a total of 4 + 13 = 17 cups of paint.
To calculate the percent of red paint, we divide the amount of red paint (13 cups) by the total amount of paint (17 cups) and multiply by 100 to get the percentage:
Red paint percentage for Casho = (13 cups / 17 cups) * 100 = 76.47% (rounded to two decimal places)
Comparing the percentages, we can see that Casho's purple paint will be redder because Casho's paint has a higher percentage of red paint (76.47%) compared to Isaiah's paint (70%).
Therefore, based on the percent of red paint, Casho's purple paint will be redder than Isaiah's.
for such more question on percent
https://brainly.com/question/24877689
#SPJ8
the next model of a sports car will cost 14.4% more than the current model the current model cost $41,000 how much would a price increase in dollars what would the price of the next model?
Answers
Given that the current model of the car cost;
\(\text{ \$41,000}\)We are informed that the next model of a sports car will cost 14.4% more than the current model.
The price increase in dollars will then be given as;
\(\begin{gathered} \frac{14.4}{100}\times41000 \\ =\text{ \$}5904 \end{gathered}\)Answer 1: Price increase in dollars is $5904
The cost of the next model will then be the sum of the current model and the price increase in dollars.
This would give;
\(\text{ \$41000+\$5904=\$46904}\)Answer 2: The cost of the next price model is $46904
An incomplete table of values for an exponential function is shown. The exponential function is of the form y=a\cdot b^x where a is a real number such that a\ne0 and b is a positive real number not equal to 1.
Enter the values of a and b in the boxes given below, then complete the table with possible values for the exponential function.
X- 0-1-2-3
Y-96------
Answers
Answer:
−3−99
because if
+0−1−2−3−96
x+0−1−2−3−96
−99−3
The required exponential function will be \(f(x) =9(\frac{2}{3} )^x\) with a and b values 9 and 2/3 respectively.
The given exponential function is:
\(f(x) = ab^x\)
What is a function?A function is a rule that relates two variables.
Point (0,9) lies on the graph of the given function.
So, \(9=ab^0\)
\(a=9\)
So, f(x) becomes \(f(x)=9b^x\)
Point (1,6) also lies on the graph of the given function.
So, \(6=9b\)
\(b=\frac{2}{3}\)
So, the required function will be \(f(x) =9(\frac{2}{3} )^x\)
Therefore, The required exponential function will be \(f(x) =9(\frac{2}{3} )^x\) with a and b values 9 and 2/3 respectively.
To get more about exponential function visit:
https://brainly.com/question/2456547
4.
Mrs. Smith has a cardboard box in the shape of a rectangular prism. She plans to cover it with
paper. The dimensions of the box are 3in by 4in by 6in. What is the minimum amount of paper
needed to completely cover the box?
Answers
Answer:
108 inches²
Step-by-step explanation:
Rectangular prism = cuboid
To find how much paper is required to cover the box, we need to find the TSA of the cuboid.
TSA of cuboid = 2 [LB + LH + HB] = 2 [ (3×4) + (3×6) + (4×6) ] = 2 [ 12+18+24 ] = 2 × 54 = 108 inches²
Question 10 of 10
How does the graph of f (x) 3x +2 +4 relate to its parent function?
A. The parent function has been compressed.
B. The parent function has been translated up.
C. The parent function has been stretched.
D. The parent function has been translated to the left.
SUBMIT
Answers
The graph of f(x) relate to its parent function by B. The parent function has been translated up.
How does the graph of f(x) relate to its parent function?Given that
f(x) = 3x +2 +4
When evaluated, we have
f(x) = 3x + 6
The parent function of the above is
f(x) = 3x
When f(x) = 3x is compared to f(x) = 3x + 6, we have
Difference = 6
This means that the parant function is translated up by 6 units
Read more about transformation at
https://brainly.com/question/1548871
#SPJ1
2/3 ounce servings are in 5 1/2 ounces of oatmeal
Answers
Answer: 4/33
Step-by-step explanation:
just divide
Answer:
The answer is 4/33.
Step-by-step explanation:
to get this you just have to divide.
you're welcome.
Jadan has a drawer of different colored t-shirts. He has 4 white t-shirts, 5 black t-shirts, 3 red t-shirts and 2 blue t-shirts. He is going out of town and is in need of 2 t-shirts. What is the probability that he will randomly choose a white t-shirt without replacement and then choose a blue t-shirt?
Answers
Answer:
25%
Step-by-step explanation:
Add or subtract the following monomials 25x-(-30x)
Answers
Answer:
Negative times a negative equals a positive
25x + 30x
55x
Define a storehouse of value. An item that maintains its worth over time.
Answers
The equation n = 0.03t² -0.6t+ 3.93, models, n , the number (in millions) of people who moved to another state in the year that is t years since 1990. The table below shows some of the data that were used to find this model. Year 1995 1998 2001 2004 2006 Number of People Who Moved to Another State (millions) a. When t O what is the value of n ? What does it mean in this situation? Select an answer 1.7 1.1 1.0 1.5 2.1 b. Estimate the number of people who moved to another state in 2005. million (Round to the nearest tenth of a million.) c. Predict the number of people who moved to another state in 2014. million (Round to the nearest tenth of a million.)
Answers
When t = 0, the value of n is approximately 3.93 million. The estimated number of people who moved to another state in 2005 is approximately 1.68 million. The predicted number of people who moved to another state in 2014 is approximately 6.81 million.
we need to substitute the given values of t (years since 1990) into the equation n = 0.03t² - 0.6t + 3.93. Let's calculate the values accordingly:
a. When t = 0 (which corresponds to the year 1990), we substitute this value into the equation:
n = 0.03(0)² - 0.6(0) + 3.93
n = 0 + 0 + 3.93
n ≈ 3.93
So, when t = 0, the value of n is approximately 3.93 million. In this context, it means that in the year 1990, around 3.93 million people moved to another state.
b. To estimate the number of people who moved to another state in 2005 (t = 2005 - 1990 = 15), we substitute this value into the equation:
n = 0.03(15)² - 0.6(15) + 3.93
n = 0.03(225) - 9 + 3.93
n = 6.75 - 9 + 3.93
n ≈ 1.68
Therefore, the estimated number of people who moved to another state in 2005 is approximately 1.68 million.
c. To predict the number of people who moved to another state in 2014 (t = 2014 - 1990 = 24), we substitute this value into the equation:
n = 0.03(24)² - 0.6(24) + 3.93
n = 0.03(576) - 14.4 + 3.93
n = 17.28 - 14.4 + 3.93
n ≈ 6.81
Hence, the predicted number of people who moved to another state in 2014 is approximately 6.81 million.
For more such questions on number , Visit:
https://brainly.com/question/26460978
#SPJ11
please help me with this dont guess pls!

Answers
Answer:
B
Step-by-step explanation:
Answer:
3357
Step-by-step explanation:
Why does Paine use the example of
Massanello?
O to compare the situation to a man who insisted on
independence from Spain and then became king
O to illustrate the importance of protesting loudly in a public
place to get support for the fight for freedom
O to identify a hero that the American colonists can look up
to and model their fight after
O to prove that even simple fishermen have something
important to contribute to society
Answers
Answer: A
Step-by-step explanation: I just did it.
Please help!!
One thousand people stood in a very large circle. Each person wore a sign on their back
with a numeral from 1 to 1000, in a clockwise sequence. They began counting off. The
first person, person A, said "one-in," and remained in the circle. Person B, the person to
the left of A, said "two-out," and left the circle. The person to the left of B, person C, said
"three-in," and remained in the circle. The person to the left, person D, said "four-out,"
and stepped out of the circle.
So it continued with each person wearing an odd number saying "in," and remaining in
the circle, and with every person wearing an even numeral leaving the circle.
It was easy to visualize who remained in the circle when the count off made it all the way
around back to the first person. Since the last person said "one thousand-out," person A,
the first person, said "one-in," and stayed in, while person C, now the next person, said
"three-out," and left the circle. This process would keep going on and on until only one
person was left in the circle.
Who was the last person standing?
Answers
The person who gets to say the last number, 1000, will be Person 6.
Here, we have,
In this scenario, we have seven people sitting in a circle and counting clockwise. The goal is to determine which person will say the last number when they reach 1000. To solve this problem, we can use the concept of modular arithmetic.
When dividing 1000 by the total number of people (7), we get a quotient of 142 and a remainder of 6 (1000 = 142*7 + 6). This means that after completing 142 full rounds of counting, the group will have reached the number 994 (142*7). In the next round, they will continue counting from 995 to 1000.
Since the remainder is 6, it indicates that the last number (1000) will be spoken by the person sitting 6 positions after the first person in the circle (clockwise). In other words, Person 1 says numbers 1, 8, 15, and so on, while Person 6 will say 6, 13, 20, and so on.
To learn more about modular arithmetic click here
brainly.com/question/29022762
#SPJ1
complete question:
10) Seven people sit in a circle and begin counting clockwise starting from 1.Each person in the group is keeping track of the numbers she is saying (e.g. 1,8, 15...) If they continue in this way, counting on and on, until they reach 1000, which person will get to say the last number
A neighborhood is trying to set up school carpools, but they need to determine the number of students who need to travel to the elementary school (ages 5-10), the middle school (ages 11-13), and the high school (ages 14-18). A histogram summarizes their findings:
Histogram titled Carpool, with Number of Children on the y axis and Age Groups on the x axis. Bar 1 is 5 to 10 years old and has a value of 3. Bar 2 is 11 to 13 years old and has a value of 7. Bar 3 is 14 to 18 years old and has a value of 4.
Which of the following data sets is represented in the histogram?
{3, 3, 3, 7, 7, 7, 7, 7, 7, 7, 4, 4, 4, 4}
{5, 10, 4, 11, 12, 13, 12, 13, 12, 11, 14, 14, 19, 18}
{5, 6, 5, 11, 12, 13, 12, 13, 14, 15, 11, 18, 17, 13}
{3, 5, 10, 11, 13, 7, 18, 14, 4}
Answers
The correct answer is that the data set {3, 7, 4} is represented in the given histogram.(option-a)
The given histogram represents the number of children in each age group who need to travel to school. Since the histogram has only three bars, we can conclude that there are only three age groups.
The first bar represents children aged 5-10, of which there are 3. The second bar represents children aged 11-13, of which there are 7. The third bar represents children aged 14-18, of which there are 4.
Therefore, the data set that is represented in the histogram is:
{3, 7, 4}
None of the other data sets given match the values in the histogram. The first data set has duplicate values and is not sorted by age group. The second data set includes ages that are not represented in the histogram. The third data set has values for ages 6, 11, 12, 13, 14, 15, 17, and 18, but the histogram does not have bars for all those ages. (option-a)
For such more questions on histogram
https://brainly.com/question/32761368
#SPJ8
In the following function defined by an equation in the form y = ax^2+ bx+c, identify the values of a, b, and c.
y = 5x²+2x-1
Answers
Im pretty sure it’s B
The sum of the first two terms of a G.P is 5/2 , and the sum of the first four terms is 65/18. Find the G.P if r>0
Answers
Answer:
Common ratio r = \(\dfrac{2}{3}\)
Sequence is described by
\(a_n = \dfrac{3}{2}\cdot \left(\dfrac{2}{3}\right)^{n-1}\\\)
Step-by-step explanation:
\(S_n = \dfrac{a_1(1-r^n)}{1-r}\)
where
r = common ratio
a₁ = first term
Sum of first two terms
\(S_2 = \dfrac{a_1(1-r^2)}{1-r}\)
Sum of first four terms:
\(S_4 = \dfrac{a_1(1-r^4)}{1-r}\)
\(\dfrac{S_4}{S_2} = a_1 \cdot \dfrac{1-r^4}{1-r} \div a_1 \cdot \dfrac{1-r^2}{1-r}\\\)
To divide, flip the divisor and multiply
\(\dfrac{S_4}{S_2} =\dfrac{a_1(1-r^4)}{1-r} \times \dfrac{1-r}{a_1(1-r^2)}\)
The a₁ and (1-r) terms cancel out from numerator and denominator leaving
\(\dfrac{S_4}{S_2} =\dfrac{1-r^4}{1-r^2} \cdots [1]\)
Using the identity
\(a^2 - b^2 = (a- b)(a+b)\)
\(1- r^4 = 1^4 - r^4 = (1^2 - r^2)(1^2+r^2) = (1-r^2)(1+r^2)\)
Plugging this into equation 1 we get
\(\dfrac{S_4}{S_2} =\dfrac{(1-r^{2})(1+r^{2})}{1-r^{2}}\)
The \(1- r^2\) terms cancel out leaving:
\(\dfrac{S_4}{S_2} =1 + r^2\)
We are given
\(S_4 =\dfrac{65}{18}\\\\S_2 = \dfrac{5}{2}\)
\(\dfrac{S_4}{S_2} = \dfrac{65}{18} \div \dfrac{5}{2}\)
To divide, flip the denominator \(\dfrac{5}{2}\) and multiply
\(\dfrac{S_4}{S_2} = \dfrac{65}{18} \times \dfrac{2}{5}\\\\= \dfrac{13}{9}\)
Therefore
\(1 + r^2 = \dfrac{13}{9}\\\\r^2 = \dfrac{13}{9} - 1\\\\= \dfrac{13}{9} - \dfrac{9}{9}\\\\= \dfrac{4}{9}\)
\(r = \sqrt{\dfrac{4}{9}}\\\\= \dfrac{\sqrt{4}}{\sqrt{9}}\\\\= \dfrac{2}{3}\)
So the common ratio
\(r = \dfrac{2}{3}\)
To find the first term we have sum of first two terms = 5/2
\(S_2 = \dfrac{a_1(1-r^2)}{(1-r)} = a_1 (1+ r)\)
Plugging in knowns
\(\dfrac{5}{2} = a_1(1+\dfrac{2}{3})\\\\= a_1 \cdot \dfrac{5}{3}\)
Multiply both sides by 3/5 to get
\(a_1 = \dfrac{5}{2} \times \dfrac{3}{5}\\\\a_1 = \dfrac{3}{2}\)
The nth term of a GP is
\(a_n = a_1 \cdot r^{n-1}\\\)
Plugging in the values obtained
\(a_n = \dfrac{3}{2}\cdot \left(\dfrac{2}{3}\right)^{n-1}\\\)
Which description is paired with its correct expression?
four less than the quotient of a number cubed and seven, increased by three; 4-2+3
five times the difference of a number squared and six; 5(6-n²)
nine more than the quotient of six and a number cubed, decreased by four; 8+²-4
9+
O twice the difference of nine and a number squared; 2(9-n²)
Answers
The correct pairings are:
a) Four less than the quotient of a number cubed and seven, increased by three: (n³/7) - 4 + 3
b) Five times the difference of a number squared and six: 5(n² - 6)
c) Nine more than the quotient of six and a number cubed, decreased by four: (6/n³) + 9 - 4
d) O twice the difference of nine and a number squared: 2(9 - n²)
The correct pairings of descriptions and expressions are as follows:
Four less than the quotient of a number cubed and seven, increased by three: (n³/7) - 4 + 3
This expression represents taking a number, cubing it, dividing the result by seven, subtracting four, and then adding three.
Five times the difference of a number squared and six: 5(n² - 6)
This expression represents taking a number, squaring it, subtracting six, and then multiplying the result by five.
Nine more than the quotient of six and a number cubed, decreased by four: (6/n³) + 9 - 4
This expression represents taking the cube of a number, dividing six by the cube, adding nine, and then subtracting four.
O twice the difference of nine and a number squared: 2(9 - n²)
This expression represents taking a number, squaring it, subtracting it from nine, and then multiplying the result by two.
For more questions on quotient
https://brainly.com/question/11418015
#SPJ8
An automatic car wash takes exactly 5 minutes to wash a car. On average, 10 cars per hour arrive at the car wash. Suppose that, 30 minutes before closing time, five cars are in line. If the number of cars in any time interval follows a Poisson distribution, and if the car was is in continuous operation until closing time, what is the probability that anyone will be in line at closing time
Answers
Answer:
0.9595724
Step-by-step explanation:
Time taken to wash a car (μ) = 5 minutes
Hence, Number of cars washed per hour = 60/5 = 12 cars
If 5 cars arrive, 30 minutes to closing ; it takes 25 minutes to finish up ;
If 1 more car arrives, then it takes exactly 30 minutes
Hence, there will be no one in line at closing ;
IF 0 or 1 car arrives, if more than 1 car arrives, then there will be people in line at closing.
Hence, probability of waiting in line at closing :
1 - [p(0) + p(1)]
Using poisson :
P(x) = [(e^-μ) * (μ^x)] / x!
If x = 0
P(0) = [(e^-5) * (5^0)] / 0!
P(0) = (0.0067379 * 1) / 1
P(0) = 0.0067379
X = 1
P(1) = [(e^-5) * (5^1)] / 1!
P(0) = (0.0067379 * 5) / 1
P(0) = 0.0336897
Hence,
1 - (0.0067379 + 0.0336897)
1 - 0.0404276
= 0.9595724
Hence, the probability that anyone would be in the car washing line after closing is 0.9595724
Give your answer in scientific notation using only WHOLE numbers.

Answers
The number of pennies weighing as much s earth is 193 × 10²⁴
What are index forms?Index forms are described as described as those forms that are used to represent numbers that are too large or small in more proper ways.
Other names for index forms are scientific notation and standard forms.
What is ratio?Ratio is described as the comparison of numbers or variables on the basis of their size.
It shows how many times one number contains another.
From the information given, we have that;
The earth weighs = 5. 972 × 10 ²⁴ kilograms
The penny weighs = 3.1 × 10 ⁻³ kilograms
Divide the values
= 5. 972 × 10 ²⁴/3.1 × 10 ⁻³
= 1.93 × 10 ²⁶
= 193 × 10²⁴
Learn about index forms at: https://brainly.com/question/15361818
#SPJ1
Help asap giving branlist!!!
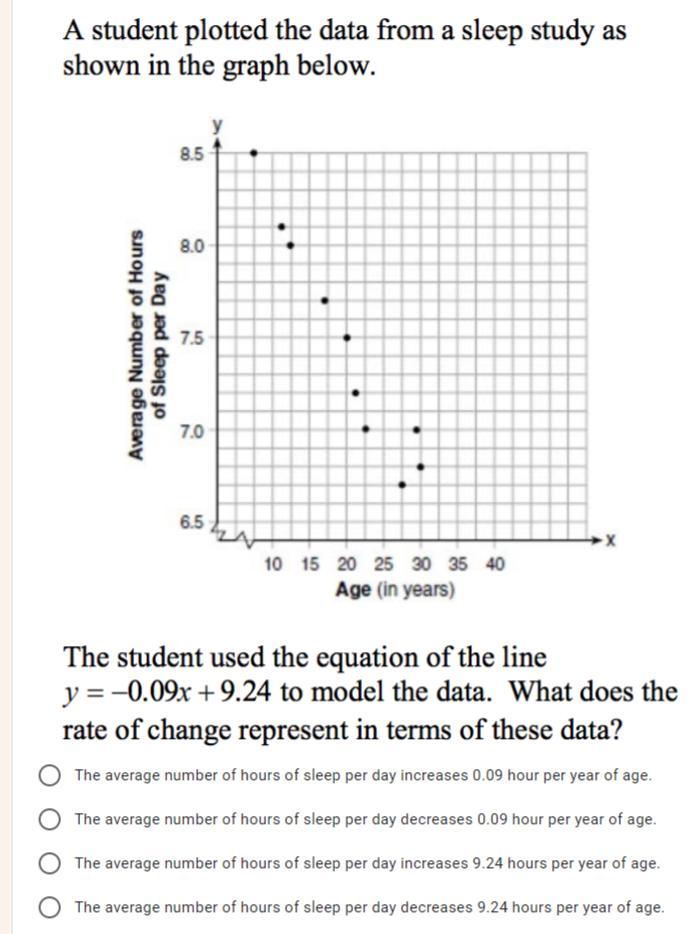
Answers
Answer:
Option 2
Step-by-step explanation:
Because the slope is -0.09 the answer is the second option. A negative slope means a decrease.
Solve for x.
89(54x−36)+2=−34(−40+16x)+90x
Answers
The value of x for the equation is 0.35.
What is simplification?Simply put, to simplify is to make something simpler. Simplifying an equation, fraction, or issue in mathematics entails taking something complex and making it simpler. The issue is made simpler by calculations and problem-solving strategies. We can simplify fractions by removing all common elements from the numerator and denominator and putting the fraction in its simplest/lowest form.
Given equation,
89 (54x − 36) + 2 = -34( −40 + 16x) + 90x
using PEMDAS
solving Parentheses first,
89(54x) - 36(89) + 2 = -34(-40) + 16x(-34) +90x
4806x - 3204 +2 = -1360 - 544x + 90x
4806x + 544x - 90x = -1360 + 3204 -2
5260x = 1842
x = 0.35
Hence the value of x is 0.35.
Learn more about simplification;
https://brainly.com/question/2804192
#SPJ1
A
X
Find the value of x.
D
X+2
x = [?]
B
3
E
2
C
![AXFind the value of x.DX+2x = [?]B3E2C](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/NizqkSoyno5R9ihZJuX6BBJHmDyqL8LN.png)
Answers
Answer:
x = 4
Step-by-step explanation:
if a line is parallel to a side of a triangle and it intersects the other two sides then id divides those sides proportionally.
DE is such a line , then
\(\frac{BD}{AD}\) = \(\frac{BE}{EC}\) ( substitute values )
\(\frac{x+2}{x}\) = \(\frac{3}{2}\) ( cross- multiply )
3x = 2(x + 2)
3x = 2x + 4 ( subtract 2x from both sides )
x = 4
5: The US Postal Service believes less than 13% of the packages mailed during the
holiday rush are delivered late. To test this claim, it randomly selects 228 packages
during the holiday rush and finds that 24 are delivered late. Test the US Postal Service’s
claim at α = .01.
What type of error could be made based on your decision in step 5 of the above
hypothesis test?
Answers
There are two types of errors that could be made:
a Type I error and a Type II error.
We have,
In step 5 of the hypothesis test, we make a decision to either reject or fail to reject the null hypothesis.
If we reject the null hypothesis, there are two types of errors that could be made:
a Type I error and a Type II error.
A Type I error occurs when we reject a true null hypothesis.
In this context, it means that we conclude that the percentage of packages delivered late is greater than 13% when in reality it is not.
This error is also known as a false positive.
A Type II error occurs when we fail to reject a false null hypothesis.
In this context, it means that we conclude that the percentage of packages delivered late is less than or equal to 13% when in reality it is greater than 13%. This error is also known as a false negative.
The probability of making a Type I error is denoted by α, which is given in the problem statement as α = 0.01.
Therefore, if we reject the null hypothesis, there is a 1% chance that we are making a Type I error.
Thus,
The probability of making a Type II error depends on the effect size, sample size, and significance level of the test.
Learn more about hypothesis testing here:
https://brainly.com/question/30588452
#SPJ1
Which word describes the slope of a line

Answers
Answer:
A. positive
Step-by-step explanation:
A line that goes up from down has a positive slope.
Step by step explanation